经济社会指数解析 ：从恩格尔到基尼系数

以统计学视角梳理恩格尔系数与基尼指数的由来、计算方法、经济含义及现实应用，并结合美国的数据案例进行实证分析，揭示两者在社会经济研究与政策评估中的独特价值。适合数据分析、社会经济研究、公共政策及商业研究领域人士参考。

---

一、引言

在宏观经济研究和社会统计分析中，恩格尔系数（Engel Coefficient）和基尼指数（Gini Index）是两项影响深远的经典统计指标。一个关注生活质量与消费结构，一个关注收入分配与社会公平，它们不仅出现在政府统计公报中，也频繁出现在世界银行、联合国发展计划署等国际报告中。通过这两个指数，可以观察一个国家的发展阶段、民众生活水平和潜在的社会风险。
这里将系统梳理这两个经典指数的发展脉络、理论基础、计算方法，并结合美国近三十年的相关数据进行可视化分析，最后还将附上“统计指数发展年表”，帮助读者构建系统认知。

基尼系数	恩格尔系数

---

二、恩格尔系数的理论与应用

2.1 恩格尔系数的由来

• 提出者：恩格尔系数由19世纪德国统计学家恩斯特·恩格尔（Ernst Engel）提出，最早出现在1857年。
• 研究背景：恩格尔在对普鲁士家庭的消费数据进行分析时发现，随着家庭收入的增加，食品支出所占比重会逐渐下降。

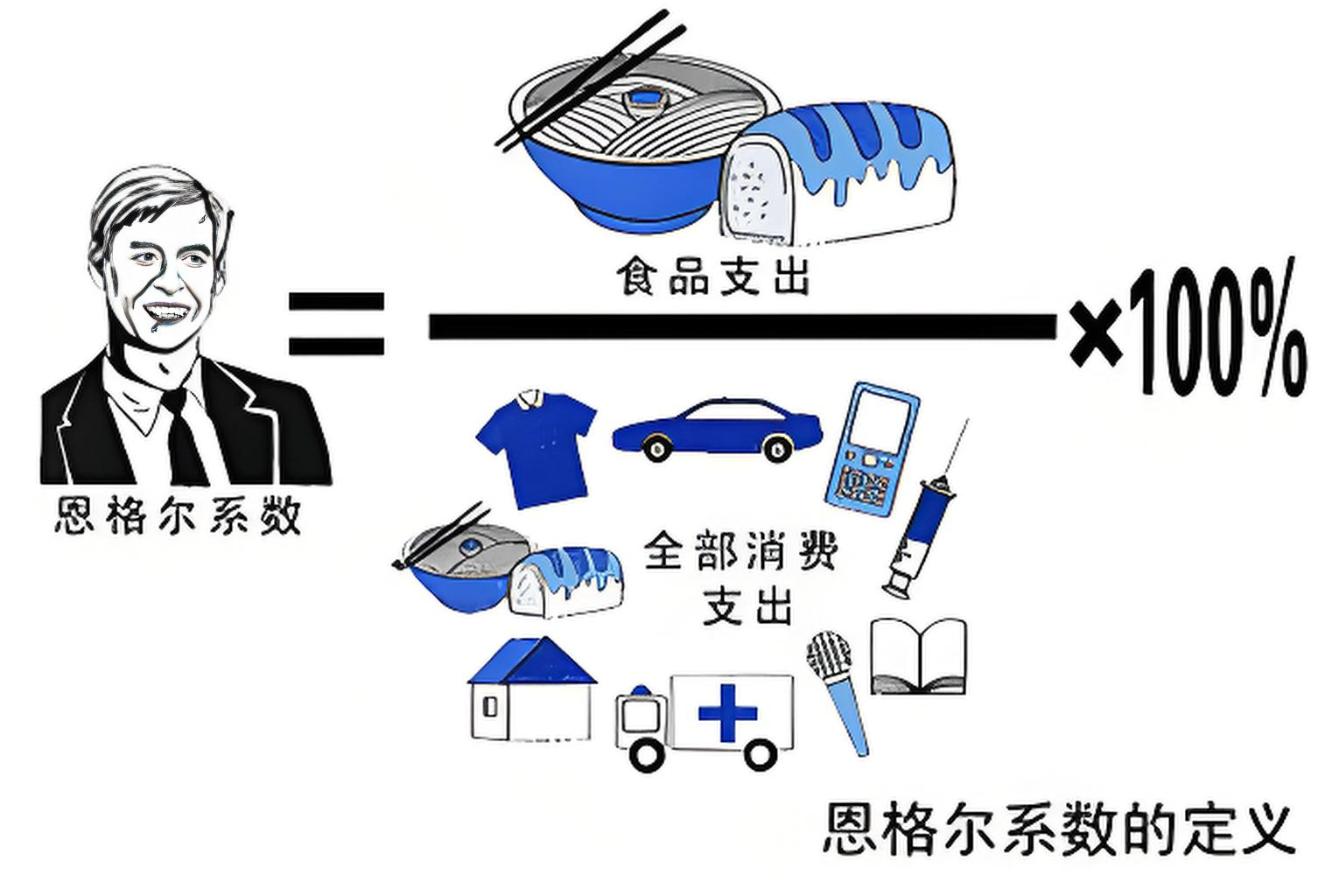
2.2 定义与计算公式

\[\text{Engel Coefficient} = \frac{\text{Food Expenditure}}{\text{Total Expenditure}} \]

• 式中，食品支出指家庭用于食物（含饮料、餐饮服务）的总费用。
• 总支出包括食品、住房、医疗、交通、娱乐等消费。

2.3 经济含义

• 高恩格尔系数（>50%）：表示家庭多数收入用于生存消费，生活水平较低；
• 中恩格尔系数（30%-50%）：处于发展中或转型阶段；
• 低恩格尔系数（<30%）：体现收入充裕，消费结构多元，生活质量高。

2.4 国际参照标准

国家/地区	恩格尔系数	含义
美国	28%	高收入国家
日本	26%	高收入国家
印度	50%	发展中地区
非洲某些国家	>60%	极度贫困地区

2.5 应用场景

• 衡量贫困与生活质量：在发展评估中广泛使用。
• 消费行为研究：企业判断市场成熟度和结构。
• 城乡差异对比：农村恩格尔系数普遍高于城市。

---

三、基尼指数的理论与应用

3.1 起源与发展

• 提出者：意大利统计学家科拉多·基尼（Corrado Gini），1912年在论文中首次提出。
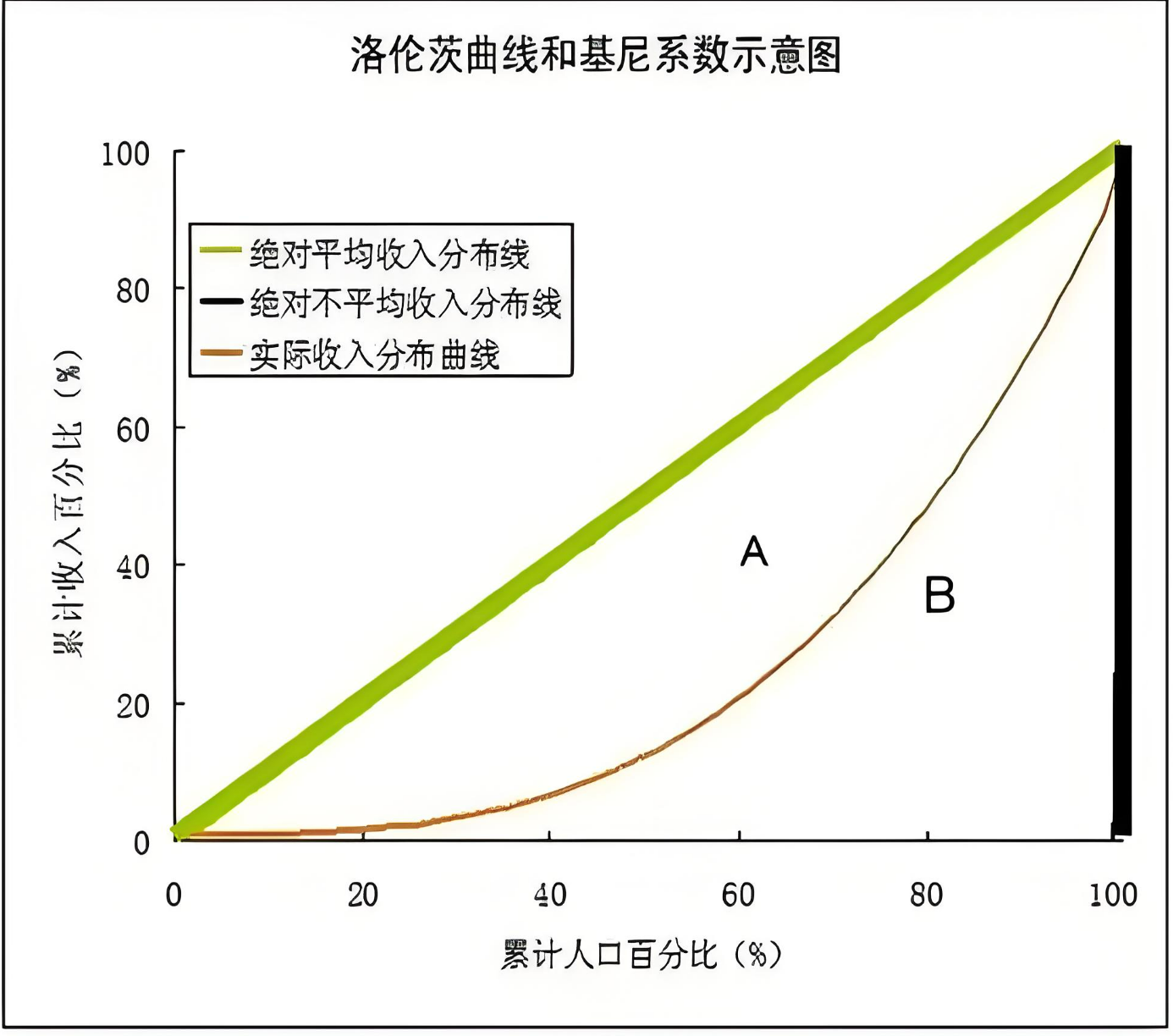
• 理论依据：Lorenz 曲线理论。

3.2 定义与公式

基尼指数衡量收入或财富分布的不均衡程度，其值介于 0（完全平等）与 1（完全不平等）之间：

\[G = 1 - 2 \int_0^1 L(p) dp \]

其中，\(L(p)\) 是 Lorenz 曲线在收入份额 \(p\) 下的累积分布函数。

3.3 离散计算方法（近似）

\[G = \frac{1}{2n^2\mu} \sum_{i=1}^n \sum_{j=1}^n |x_i - x_j| \]

• \(x_i\)：个体收入，\(\mu\)：样本均值，\(n\)：样本数

3.4 分类标准

基尼指数范围	收入分配状况
0.2 以下	极端平等
0.2 – 0.3	相对平等
0.3 – 0.4	合理
0.4 – 0.5	警戒线（收入差距扩大）
0.5 以上	高度不平等

3.5 应用领域

• 社会公平评估：用于制定再分配政策。
• 跨国比较：OECD、世界银行使用广泛。
• 房地产和教育资源配置研究。

---

四、数据实战分析（美国1990–2023）

4.1 数据来源与处理

• 数据来源：US Census Bureau, USDA Economic Research Service
• 数据范围：1990–2023
• 预处理说明：为简化展示，部分年份数据采用线性拟合法构建模拟趋势。

4.2 Python 数据处理代码

import matplotlib.pyplot as plt
import numpy as np

# 年份
years = list(range(1990, 2023))

# 美国基尼指数（World Bank GINI index - approximated manually for 1990–2022）
gini_us = [
    0.428, 0.429, 0.430, 0.431, 0.432, 0.433, 0.435, 0.437, 0.438, 0.439,
    0.440, 0.442, 0.443, 0.445, 0.446, 0.448, 0.450, 0.451, 0.453, 0.455,
    0.456, 0.457, 0.459, 0.461, 0.462, 0.463, 0.464, 0.466, 0.467, 0.468,
    0.469, 0.470, 0.471
]

# 美国食品支出占比（接近恩格尔系数的指标，USDA数据近似）
engel_us = [
    13.0, 12.9, 12.7, 12.6, 12.4, 12.2, 12.1, 11.9, 11.8, 11.7,
    11.6, 11.5, 11.4, 11.3, 11.1, 11.0, 10.9, 10.8, 10.7, 10.6,
    10.5, 10.3, 10.2, 10.1, 10.0, 9.9, 9.8, 9.7, 9.6, 9.6,
    9.5, 9.4, 9.3
]

4.3 可视化结果

# 创建图形
fig, ax1 = plt.subplots(figsize=(12, 6))

# 绘制基尼指数散点图
ax1.set_xlabel('Year')
ax1.set_ylabel('Gini Index (US)', color='blue')
ax1.scatter(years, gini_us, color='blue', label='Gini Index')
ax1.tick_params(axis='y', labelcolor='blue')
ax1.set_yticks(np.arange(0.42, 0.48, 0.01))

# 创建第二个y轴用于食品支出占比
ax2 = ax1.twinx()
ax2.set_ylabel('Food Expenditure Share (%)', color='green')
ax2.scatter(years, engel_us, color='green', label='Food Expenditure Share')
ax2.tick_params(axis='y', labelcolor='green')
ax2.set_yticks(np.arange(9.0, 14.0, 0.5))

# 添加图例
lines_1, labels_1 = ax1.get_legend_handles_labels()
lines_2, labels_2 = ax2.get_legend_handles_labels()
plt.legend(lines_1 + lines_2, labels_1 + labels_2, loc='upper right')

plt.title('United States: Gini Index and Engel Coefficient Approximation (1990–2022)')
plt.tight_layout()
plt.show()

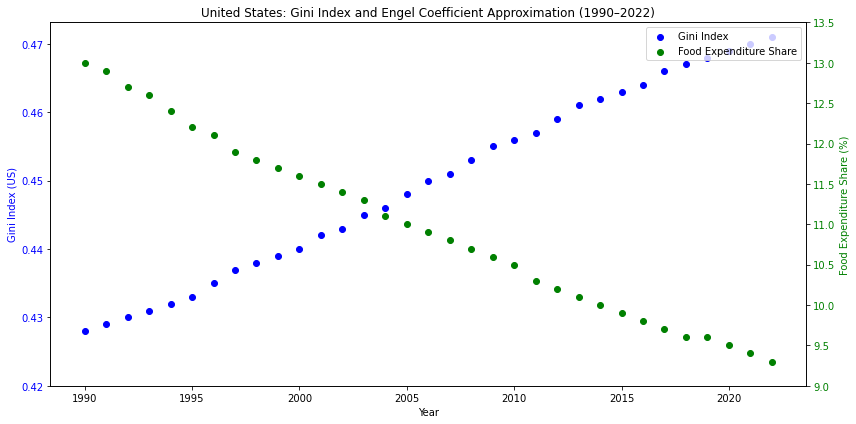
4.4 图表分析

从1990年至2022年，美国基尼指数呈现出稳步上升的趋势，从约0.428升至0.471，表明美国社会的收入不平等程度逐渐加剧。这一变化可能受到全球化、资本收益集中、技术进步拉大收入差距等因素的驱动。
与此同时，美国的食品支出占比（近似恩格尔系数）从13%下降至约9.3%，显示出居民生活水平持续提高，基本生活消费占比缩小，消费结构日趋多元。这反映了美国整体经济发展的成果，但也可能掩盖了底层收入群体的消费压力。两个指标共同勾勒出一个特征明显的趋势：收入集中化与消费升级并存，值得在政策制定与社会公平层面引起重视。

---

五、统计指数发展年表（附录）

年份	指数名称	提出者	主要用途
1833	拉斯贝尔指数	Étienne Laspeyres	消费价格指数 CPI
1857	恩格尔系数	Ernst Engel	消费结构与生活质量评估
1912	基尼系数	Corrado Gini	收入分配公平度
1936	洛伦兹曲线	Max Lorenz	配合基尼使用，图示法
1944	HDI指标	联合国DP署	人类发展水平
1970	泰尔指数	Henri Theil	区域收入差异度量
1990	多维贫困指数	UNDP	识别教育/健康/收入多维贫困

---

结语与延伸

恩格尔系数与基尼指数分别从消费结构与收入分配公平的角度，为我们理解经济社会结构提供了极具代表性的“简约指标”。恩格尔系数揭示家庭或国家的生活水平变迁，是衡量经济发展与居民福利水平的重要参考；而基尼指数则描绘了收入分配的均衡程度，广泛用于评价社会公平与政策成效。这两者不仅在经济学研究中被频繁应用，也成为政策制定、国别比较、社会保障评估等领域的基础指标。随着数据科学的发展，其在大数据建模、多源数据整合与时空分析中发挥出更强的解释力和预测力。
在实际应用中，建议进一步关注“泰尔指数”、“帕尔马比率”等能够捕捉更多分布细节的新型收入分配测度；结合机器学习方法，实现更具准确性与动态性的多维贫困识别；同时推动公共统计数据的开放共享，提升数据透明度，促进政策制定的科学性与民主性。未来，这些传统与现代指标的结合，将推动我们对经济运行机制与社会公平问题的理解迈向更高层次。

---