均值的回归——从高尔顿的回归研究谈起
你听说过“回归到均值”(Regression to the Mean)吗?这是一种常被人忽视却又普遍存在的统计现象,指的是极端值在后续观测中往往趋向于平均水平。生活中,这种现象无处不在:一位在某场比赛中表现异常出色的运动员,在下一场比赛中可能会表现平平;股市中暴涨的股票,常常在之后经历回调;学生一次考试考得特别差或特别好,下一次考试的成绩往往会更接近他们的平均水平。这种“回归”的规律,最早由19世纪英国统计学家弗朗西斯·高尔顿(Francis Galton)通过对豌豆种子大小的遗传研究发现。他注意到,大粒种子所生的子代往往粒径略小,而小粒种子的后代则略大,趋向整体种群的平均大小。高尔顿称之为“回归现象”(regression phenomenon),并由此启发了现代统计学中“回归分析”的基本思想。如今,这一现象不仅在自然科学中得到验证,也在心理学、教育学、经济学等社会科学领域广泛应用。理解它,有助于我们更理性地解读世界中“极端事件”背后的统计本质。
| 家庭编号 | 父亲身高 | 母亲身高 | 中亲身高 | 子女数量 | 子女编号 | 子女性别 | 子女身高 |
|---|---|---|---|---|---|---|---|
| 001 | 78.5 | 67.0 | 75.43 | 4 | 1 | male | 73.2 |
| 001 | 78.5 | 67.0 | 75.43 | 4 | 2 | female | 69.2 |
| 001 | 78.5 | 67.0 | 75.43 | 4 | 3 | female | 69.0 |
| 001 | 78.5 | 67.0 | 75.43 | 4 | 4 | female | 69.0 |
| 002 | 75.5 | 66.5 | 73.66 | 4 | 1 | male | 73.5 |
| 高尔顿收集的 205 对夫妇及其子女的身高数据(部分) |
引言:一颗落地的种子
我们常说:“龙生龙,凤生凤,老鼠的儿子会打洞。”在观察人类社会现象时,我们常倾向于相信出身决定成败。然而,19世纪末的英国统计学家高尔顿(Francis Galton)在研究身高遗传时,却发现了一个反直觉的规律——儿子的身高并不会完全“继承”父亲的身高优势,而是更倾向于“回归”到一个平均水平。这一发现不仅揭示了“均值回归”的现象,更是线性回归分析的滥觞。
弗朗西斯·高尔顿(Francis Galton, 1822-1911)是历史上著名的优生学家、心理学家、遗传学家和统计学家,是统计学中相关和回归等一批概念的提出者,是遗传学中回归现象的发现者。1885年,高尔顿以保密和给予金钱报酬的方式,向社会征集了 205 对夫妇及其 928 个成年子女的身高数据(Galton 1886)。Michael Friendly 从原始文献中整理后,将该数据集命名为 GaltonFamilies,放在 R 包 HistData (Friendly 2021) 内,方便大家使用。
这里以高尔顿的“回归到均值”研究为起点,循序渐进地讲解均值回归的统计学原理、回归模型的建立、可视化分析方法、与聚类的关系、实际案例分析,最后扩展到现代社会科学和商业数据分析中对均值回归现象的深入解读。
一、 高尔顿的身高研究
高尔顿是著名生物学家达尔文的表弟,同时也是一位对遗传学和统计学充满热情的研究者。他在19世纪末期的研究,不仅对人类遗传特征的理解产生了深远影响,也为现代统计学的重要分支——回归分析(Regression Analysis)奠定了基础。为了探究父母的身高是否会遗传给下一代,高尔顿收集了大量关于父母和子女身高的数据。为了便于分析,他创造性地提出了“中父母身高”(mid-parent height)的概念,即父母双方身高的平均值,并将其与子女的实际身高配对,绘制成一张散点图(如下高尔顿回归图所示)。
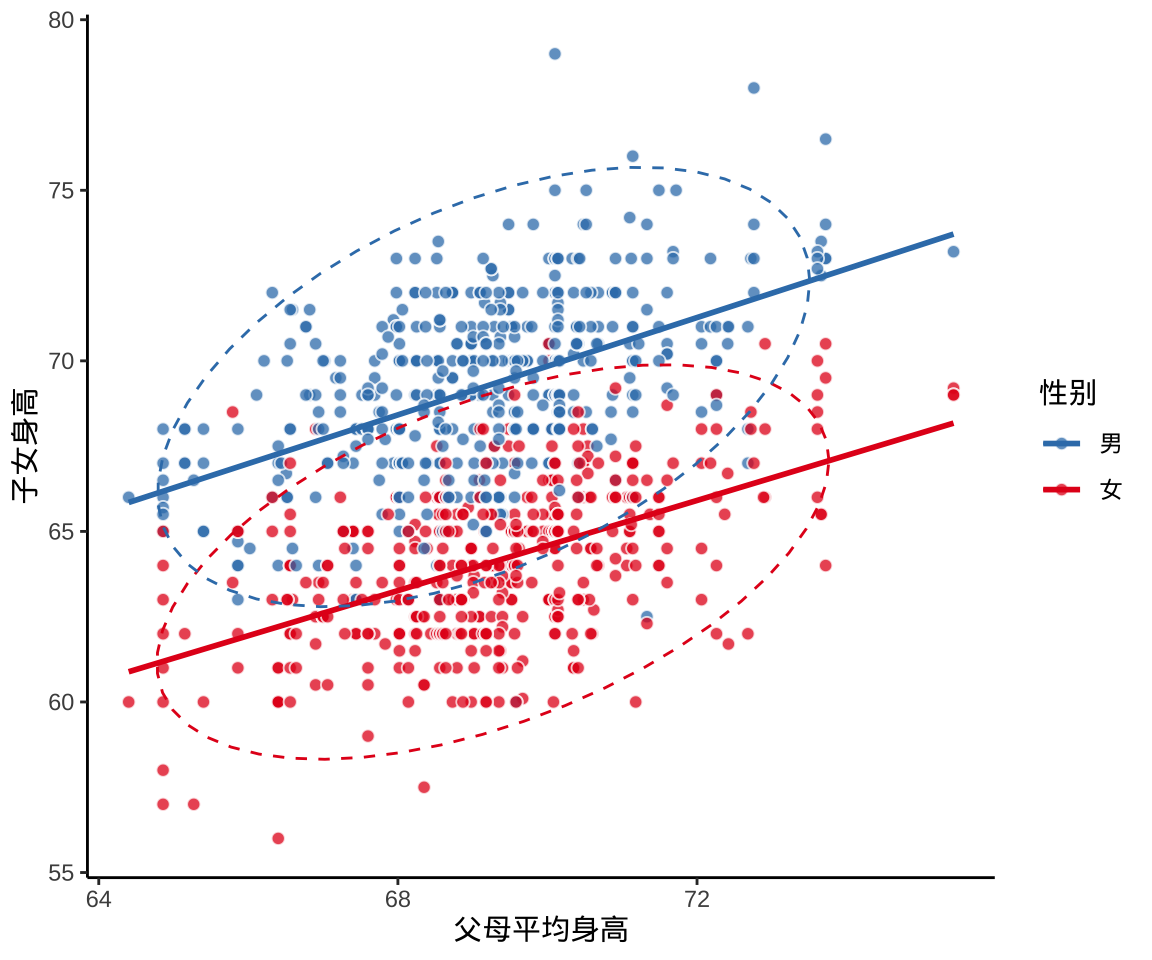
图中每一个点代表一组父母与子女的对应身高数据。从图中可以看出,虽然存在一定的正相关性——身材高的父母,其子女普遍也更高;而身材较矮的父母,子女身高也偏低——但这种关系并非一一对应。高尔顿发现一个有趣的趋势:高个父母的子女虽然也高,但通常没有父母高;而矮个父母的子女虽然也矮,但往往高于父母。这种子女身高向总体平均值靠近的现象,被他形象地称为“回归”(regression),意指“回归到均值”。
更重要的是,这种“回归”并不是某种生物上的退化,而是一种统计学的趋势,即当一个变量处于极端状态时,相关变量在下一次观测中更可能接近其平均水平。这一发现,不仅揭示了身高遗传中的统计特性,也成为了后来统计建模中的基础概念。高尔顿的研究不仅仅是一个单一观察,它激发了后人对变量间关系的深入思考,并催生了今天广泛应用于经济学、社会学、医学等领域的“线性回归模型”。他的这一贡献,也被誉为统计学发展史上的里程碑之一。
二、 什么是“均值回归”?
“均值回归”(Regression to the Mean)是一种在统计学中普遍存在却常常被误解的现象。它指出:当某个变量在第一次测量时偏离总体均值,那么在第二次测量中,它更有可能向总体平均值靠近。这个现象最早由弗朗西斯·高尔顿在研究身高遗传时提出,后来成为回归分析理论的奠基性概念。
以身高为例,假设一个群体的平均身高是 170cm。若某位父亲的身高为 190cm(远高于均值),则他的儿子往往也会比平均值高,但通常不会达到 190cm,可能是 178cm;反过来,如果父亲的身高仅为 150cm(远低于均值),儿子很可能也会偏矮,但一般高于 150cm,可能达到 162cm。也就是说:极端的个体在下一代或下次测量中更可能趋向于群体的平均水平。
这个现象不仅存在于遗传学中,在很多生活情境中也屡见不鲜。例如,一位运动员在某场比赛中发挥极佳(高于他的一贯水平),下一场可能因为种种因素而“回归正常”水平;股票价格在短期剧烈上涨后,常常也会出现下跌,回到长期均值;学生考试中意外得高分,下一次考试更可能回归其正常表现。
数学表达
均值回归的核心,可以用线性回归模型表达:
其中:
- \(X\) 表示自变量(例如父亲的身高);
- \(Y\) 表示因变量(例如儿子的身高);
- \(\alpha\) 是截距项;
- \(\beta\) 是斜率系数;
- \(\varepsilon\) 是误差项,表示所有未被解释的随机因素或变量影响。
在分析中,若斜率 \(\beta < 1\),说明每单位 \(X\) 的变动,在 \(Y\) 上的响应会打折扣,从而体现了“回归”现象。这种回归并不是由于测量错误或观察偏差造成的,而是由于自然系统中的随机变异与统计规律性共同作用的结果。
与偏误无关
“均值回归”并不意味着系统出现了偏差,也不是因为我们的测量方法出现了错误。相反,它是一种自然规律,是由于变量间存在一定相关性,但并非完美相关(即相关系数 < 1)而导致的统计趋势。它是自然界中普遍存在的波动现象,而非统计误差或实验缺陷。
我们在实际应用中要注意,不应将“回归到均值”误认为是“因果关系”。例如,在教育中,如果学生考得特别差后,老师进行谈话后成绩上升,这种上升不一定完全是谈话带来的激励效果,可能部分是均值回归的结果。类似地,股票上涨后回落、病人初诊严重之后好转、营销活动后销量短暂提升等情形,背后都可能隐藏着“均值回归”的机制。因此,理解和识别“均值回归”现象,对于科学分析数据、避免错误归因、做出合理预测,具有非常重要的现实意义。
三、从数据到模型:如何构建回归分析
以一组模拟的身高数据为例:
| 父亲身高(cm) | 儿子身高(cm) |
|---|---|
| 170 | 172 |
| 160 | 168 |
| 180 | 175 |
| 175 | 173 |
| 165 | 167 |
我们可以用线性回归分析如下:
# --------------------------
# 均值回归分析:父子身高示例
# --------------------------
# 1. 定义数据(父亲和儿子身高,单位:cm)
father <- c(170, 160, 180, 175, 165)
son <- c(172, 168, 175, 173, 167)
# 2. 拟合线性回归模型
model <- lm(son ~ father)
# 3. 输出回归模型摘要信息
cat("回归模型摘要:\n")
summary(model)
# 4. 可视化分析:绘制散点图 + 回归直线 + 完美继承线
# 设置画布参数
par(mfrow = c(1, 1)) # 单图输出
# 绘制父子身高散点图
plot(father, son,
pch = 19, # 实心点
col = "blue", # 点的颜色
xlim = c(155, 185),
ylim = c(160, 180),
xlab = "父亲身高 (cm)",
ylab = "儿子身高 (cm)",
main = "父子身高的回归分析")
# 添加回归直线(红色)
abline(model, col = "red", lwd = 2)
# 添加参考线 y = x(灰色虚线)
abline(a = 0, b = 1, col = "gray", lty = 2)
# 添加图例
legend("topleft",
legend = c("回归直线", "完全继承线"),
col = c("red", "gray"),
lty = c(1, 2),
lwd = 2)
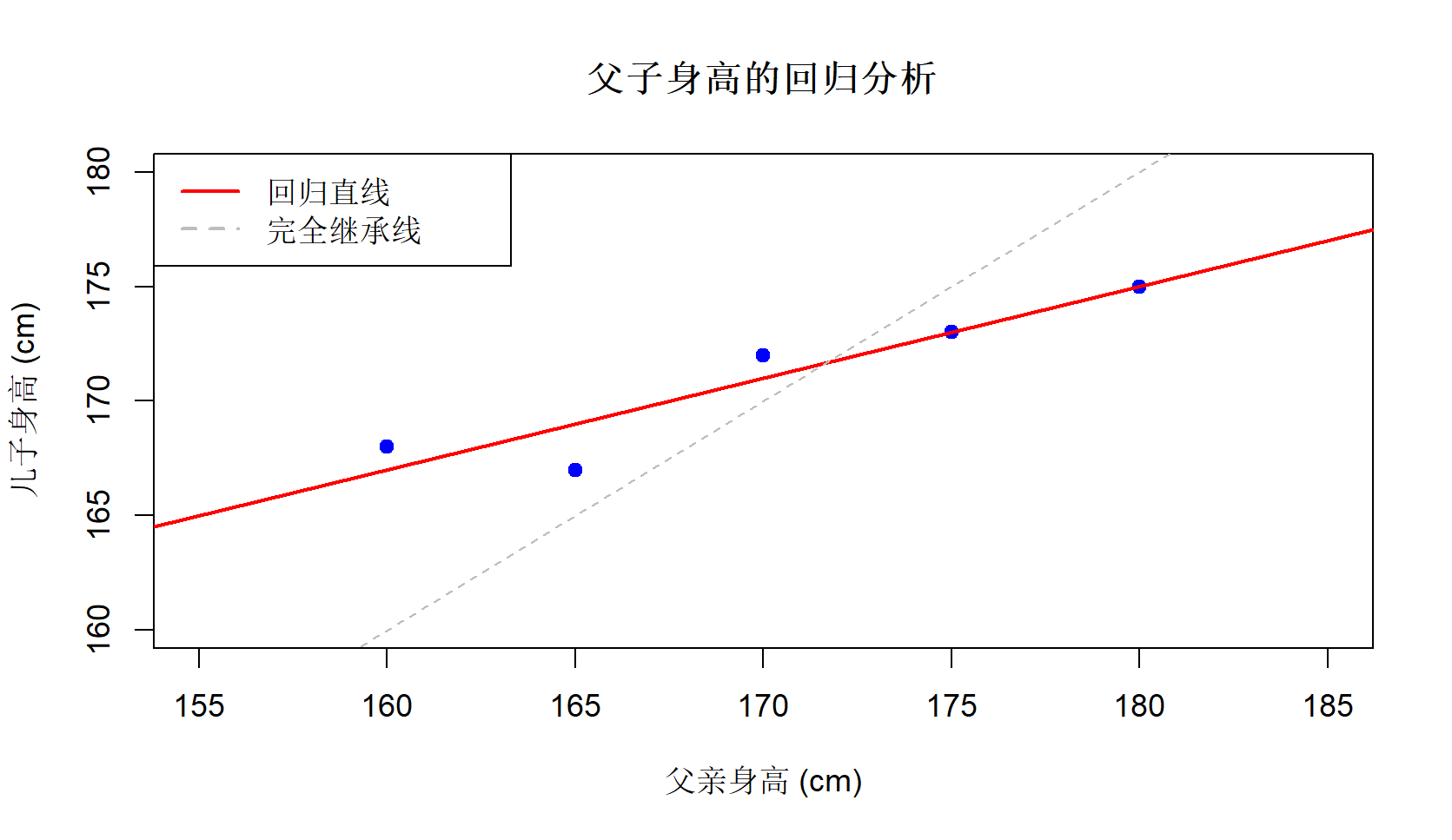
说明每多1cm父亲身高,儿子仅增加0.55cm,未能完全“继承”父亲身高。我们可以绘制回归直线:
四、 均值回归与K-means聚类的对话
“回归”与“聚类”看似属于不同类型的统计方法,回归分析属于监督学习,它试图根据输入的自变量预测目标变量;而聚类分析是无监督学习,它通过分析数据之间的相似性,将数据分为不同的组。虽然两者的技术框架不同,但它们都有一个共同的特征:数据点趋向某个“中心”,这一点在它们的核心算法和实际应用中表现得尤为突出。
回归分析中的“回归”
回归分析中的“回归到均值”是指,当自变量的测量值偏离总体均值时,经过一段时间或一次测量后,因变量更有可能回到均值附近。通过回归方程的拟合,我们能够描述因变量如何随着自变量变化,而“回归”这个词反映的是偏离均值的现象逐渐趋向均值。例如,在高尔顿的身高实验中,我们可以看到,尽管父亲的身高可能非常高或者非常矮,但子女的身高往往会回归到全体人群的平均身高。这种趋向整体均值的现象,正是“回归”现象的核心。
聚类分析中的“趋中”
K-means聚类算法与回归分析的相似之处在于,它也体现了“趋向均值”或“中心点”的过程。在K-means算法中,目标是将数据集中的所有数据点分为若干个簇,每个簇都有一个“均值中心”,即该簇中所有点的平均值。算法的工作流程通常分为以下几步:
- 初始化:首先,随机选取K个中心点,作为簇的初始中心。
- 分配阶段:接着,根据每个数据点与K个中心的距离,分配数据点到离它最近的中心点所代表的簇中。
- 更新阶段:然后,计算每个簇中所有数据点的均值,更新该簇的中心点。
- 迭代:重复第二步和第三步,直到簇的中心不再发生变化或变化非常小,表明算法收敛。
从这个过程中可以看出,每一轮的迭代都意味着数据点向簇中心“趋近”,这种趋近的过程就像是“回归”,只不过是在聚类场景中表现为数据点向均值中心的不断靠近。
“回归”与“聚类”的联系
回归是连续的聚类,聚类是离散的回归,回归与聚类尽管方法论上不同,但它们都反映了数据向某个中心点靠拢的趋势。回归的“回归”是指因变量偏离均值时,最终趋向均值;而K-means聚类中的“趋中”则是通过迭代过程,将数据点逐步归类并调整其归属的中心点,最终使得数据点越来越接近各自簇的中心。
在实际应用中,这两者的联系也时常被提及。例如,在对大量消费者行为数据进行分析时,回归分析能够帮助我们预测消费者的购买行为,而聚类分析则帮助我们识别不同类型的消费者群体。虽然两者在技术上有所不同,但它们都借助“趋近中心”的逻辑来揭示数据的潜在规律。
数据分析中的普适逻辑
无论是回归分析还是聚类分析,背后的普适逻辑是数据总是有趋中性。当我们面对复杂的数据时,常常会看到数据在某个“中心”附近集中,或者随着时间推移回到某个均值附近。这种趋中性不仅仅存在于数值数据中,也出现在社会现象、自然现象甚至是心理学研究中。例如,股市价格可能会因为短期的波动而偏离其长期趋势,但随着时间的推移,股市价格往往会回归到合理的均值区间;运动员的比赛成绩可能因为偶然因素而出现极端表现,但这些表现往往在长期赛季中趋向其正常水平。
五、回归现象的现实意义
均值回归作为统计学中广泛存在的现象,具有深刻的现实意义,尤其在多个领域表现得尤为明显。无论是体育竞技、投资市场,还是医疗康复,均值回归现象都能帮助我们更好地理解和预测复杂的动态变化。以下是几个典型应用场景的分析。
体育表现的“打回原形”
在体育竞技中,运动员的表现通常呈现出较大的波动性。某一场比赛中的超常发挥并不代表运动员能力的提升,而更可能是极端的偶然因素在起作用。比如,某位球员在一场比赛中大爆发,得分惊人,甚至创造了个人记录。然而,随后的比赛中,他们的表现往往会回归到平均水平,这种现象就体现了均值回归的规律。
这一现象不仅体现在普通比赛中,甚至在重要赛事和顶级运动员身上也同样适用。比如,某位球员被授予了赛季最有价值球员(MVP)奖项,但在接下来的赛季中,可能因种种原因表现平平,未能延续上一赛季的辉煌。这种表现上的波动,正是均值回归在体育领域的体现。即使顶尖运动员,也难以长期保持“超常”状态,最终会趋向个人的平均水平。
投资领域的“回归平庸”
在投资领域,均值回归现象尤为明显,尤其是股票市场的波动性。股市的涨跌通常具有一定的随机性,当某只股票经历大幅上涨后,其价格趋于回落,这种现象就是典型的均值回归。而当股价经历大幅下跌时,往往也会有反弹的机会,股价会逐渐回升至一个合理的水平。
投资者在评估基金经理的表现时,也必须考虑到这一现象。某个基金经理在某一年可能因投资的几只明星股票获得了显著的回报,看似是他具备了独特的投资眼光和能力。然而,未来的业绩可能并不会维持在同样高水平,反而会趋向一个更加稳定的中等水平。这种回归现象警示投资者,成功的投资不仅仅依赖于短期的表现,更要看长期的稳定性和均衡性。
医疗康复的波动期
在医疗领域,均值回归同样具有显著影响。病人在接受治疗过程中,可能会经历一段时间的快速好转,甚至一天内表现出异常良好的状态。这种快速恢复可能会被解读为治愈的迹象,然而,实际上它更可能是由于自然波动或外部因素的干扰。
例如,一位患者可能在经过几天的治疗后,状态突然大幅改善,恢复得相当迅速。然而,次日或几天后,他的健康状况可能会再次回到治疗前的正常水平或略低一些,这种波动是均值回归在医疗领域的体现。患者状态的波动并不意味着治疗无效,而是人体康复过程中固有的波动性。因此,医疗团队在评估患者恢复情况时,必须谨慎考虑这种回归现象,不应轻易将短期的波动解读为治疗效果的直接指示。
六、深度扩展:回归的未来与思考
均值回归不仅是一个经典的统计学现象,它在当今快速发展的科技和数据分析领域也发挥着越来越重要的作用。随着机器学习、深度学习和大数据分析的进步,回归分析已经不再局限于简单的线性模型,而是渗透到更多复杂的领域。在这些领域中,均值回归的基本思想得到了新的诠释和扩展,帮助我们更好地理解复杂的现象并做出更准确的预测。
机器学习中的过拟合调优
在机器学习中,尤其是监督学习中,均值回归的思想被广泛应用于调优模型的性能。过拟合是机器学习模型中常见的问题,尤其是当模型对训练数据中的噪声和极端值过于敏感时,模型表现出良好的训练精度,但却在新的数据上失去了泛化能力。为了解决这一问题,回归思想成为了一种有效的调优工具。
过拟合通常是因为模型在训练过程中过度拟合了极端数据点或噪声,这时,通过采用正则化技术、交叉验证等方法,可以使得模型的预测结果回归到一个更加平滑和稳定的状态,即均值回归。通过这种方式,模型不再过度依赖于训练集中的极端值,而是更加依赖于数据的整体趋势,从而提高了模型的泛化能力。
教育测评中的稳定指标分析
在教育测评中,均值回归的概念也得到了广泛应用。学生的考试成绩往往受到多种因素的影响,短期内的极端高分或低分可能并不能准确反映学生的真实水平。教育测评者通常会通过多次考试的均值来评价学生的真实水平,避免一次异常成绩对评估结果的过大影响。
例如,某个学生在一次数学考试中得到了非常高的分数,可能是因为临时的努力或者是偶然的运气。但如果仅仅依赖这一成绩来评估该学生的能力,可能会导致评估结果的不准确。而如果该学生在多次考试中保持稳定的成绩,那么通过均值回归的方式,我们可以得出更加准确的能力评估。这种方法有助于消除偶然因素的干扰,获得更加客观和真实的结果。
商业数据的复盘分析
在商业领域,尤其是营销活动和促销分析中,均值回归也发挥着至关重要的作用。许多公司在进行促销活动时,可能会遇到销售额的剧烈波动。某一次促销可能会带来远高于平常的销售额,这种“爆发式”的销售增长可能被误认为是长期趋势的开始。然而,从统计学的角度来看,这种极端的波动通常会回归到正常水平,促销后的销售额往往会回落。
因此,商业分析师和数据科学家在进行营销活动分析时,需要考虑回归现象。他们不能仅依赖一次促销的结果来判断未来趋势,而是需要将促销活动的效果与整体趋势结合起来,进行更为精准的预测。这就需要通过对历史数据的分析,找出促销效果的短期波动,并预测长期趋势。这种分析有助于公司合理规划未来的营销策略,避免因为过于乐观的预期导致资源的浪费。
AI视角下的回归再定义
随着人工智能和深度学习的快速发展,回归分析也经历了重要的变革。在传统的线性回归模型中,回归分析主要关注自变量与因变量之间的线性关系。然而,在深度学习和神经网络中,回归不再局限于简单的线性函数,而是可以通过非线性模型拟合更复杂的关系。尽管如此,深度学习中的回归依然保持着回归到总体趋势的核心思想——通过对大量数据的学习,找到数据的潜在模式和规律,从而做出准确的预测。
神经网络模型,尤其是深度神经网络(DNN)和卷积神经网络(CNN),通过复杂的多层结构和激活函数,可以拟合非常复杂和非线性的函数关系。在这种情况下,回归的目标不再是简单地拟合数据点,而是通过非线性拟合来找到数据的整体趋势。例如,在图像识别中,深度学习模型通过学习大量图像数据的特征,能够准确地识别图像中的内容,而这种识别过程本质上就是一种通过复杂算法找到“均值”或整体趋势的过程。
结语
“回归到均值”作为统计学中的一个重要现象,反映了数据在极端偏离后趋向平均值的自然规律。这一概念不仅仅是数学公式的推导,它在实际生活中无处不在:从个体表现的变化到群体趋势的预测,都有“回归”的影子。高尔顿通过对父母与子女身高的分析,揭示了这一现象的重要性,也为我们提供了洞察复杂社会现象的工具。
然而,均值回归不应被视为“平庸化”的象征,而是一种自然的力量。它让我们能够在数据中发现规律,并帮助我们区分随机变异与实际趋势。在分析个体与群体时,均值回归提供了一个有效的框架,帮助我们理解不确定性中的规律性。
与此类似,聚类分析中的“趋中”也展示了数据向均值中心靠拢的趋势。这表明,在统计学中,数据的趋向性和中心化是普遍的规律,贯穿了回归分析、聚类分析等多种方法。这种共性使我们在面对复杂现象时,能够采用合适的统计方法来揭示数据背后的深层次规律,从而做出更精准的预测和理性判断。

参考文献
- Galton, F. (1886). Regression towards mediocrity in hereditary stature. The Journal of the Anthropological Institute of Great Britain and Ireland, 15, 246–263.
- Freedman, D. A. (2009). Statistical Models: Theory and Practice. Cambridge University Press.
- Wikipedia contributors. Regression to the mean. https://en.wikipedia.org/wiki/Regression_toward_the_mean
- ISLR: Introduction to Statistical Learning
- 张文贤. 《应用回归分析》. 高等教育出版社.



 浙公网安备 33010602011771号
浙公网安备 33010602011771号