区间数的统计场景——区间估计

在传统数学和统计学中，数值通常被表示为一个确定的实数，这种表示方式在理论推导和理想化条件下非常有效。然而，现实世界中的很多问题远比理想环境复杂，由于测量误差、观测条件限制、环境波动、人为因素以及数据本身存在的不完全性和不确定性，使得我们往往很难用一个单一的确定值来准确刻画某一现象、状态或参数。例如，环境监测中的污染物浓度、医学诊断中的生理指标、市场经济中的价格波动等，均存在一定范围的变化或误差，无法精确确定其唯一值。为了更合理地反映这类不确定性特征，区间数（Interval Number）应运而生，成为描述模糊性、不确定性信息的一种有效数学工具。区间数通过给出上、下界的方式，定义一个数值范围，既包含了测量或估计值的不确定性，也便于在区间范围内进行数学运算和统计推断，因而被广泛应用于工程、经济、环境、医学、管理科学等多个领域。

一、区间数概述

区间数是指用一个具有上下界的闭区间来表示数值不确定性的方法，通常记作：

\[A = [a^-, a^+] \]

其中，\(a^-\) 表示区间的下界，\(a^+\) 表示区间的上界。区间数用于描述那些由于测量误差、观测条件或信息不完全性而无法确定唯一值的变量，反映出该变量可能取值的范围。当 \(a^- = a^+\) 时，区间数便退化为传统意义上的确定值。

1.1 区间数的比较

由于区间数本身具有区间范围，因此其比较方式与实数不同。常用的比较方法有以下几种：

• 包含关系比较
  若区间 \(A=[a^-, a^+]\) 完全包含于区间 \(B=[b^-, b^+]\)，即 \(a^- \geq b^-\) 且 \(a^+ \leq b^+\)，则称 \(A \subseteq B\)。
  若区间 \(A\) 与区间 \(B\) 无重叠，即 \(a^+ < b^-\) 或 \(a^- > b^+\)，可判断其相对大小。

• 均值比较
  将区间的中心值（即均值）作为比较依据，若 \(\bar{A} = \frac{a^- + a^+}{2} > \bar{B} = \frac{b^- + b^+}{2}\)，则认为 \(A\) 大于 \(B\)。

• 宽度比较
  区间的宽度 \(w(A) = a^+ - a^-\) 可以用来衡量不确定性程度，宽度越大，不确定性越高。

1.2 区间数的基本运算

区间数在加、减、乘、除等运算中，有不同于普通实数的运算规则：

• 加法

  \[A + B = [a^- + b^-, a^+ + b^+] \]

• 减法

  \[A - B = [a^- - b^+, a^+ - b^-] \]

• 乘法
  若 \(A, B \geq 0\)，则：

  \[A \times B = [a^- b^-, a^+ b^+] \]

  若存在负数，则需考虑所有可能组合，取最小与最大值作为新的上下界。

• 除法
  若 \(0 \notin B\)，则：

  \[A \div B = \left[ \frac{a^-}{b^+}, \frac{a^+}{b^-} \right] \]

通过这些运算规则，区间数不仅可以进行数学计算，还能保留计算过程中的不确定性范围，避免信息丢失，广泛应用于不确定性计算、区间估计和模糊决策等领域。

1.3 区间数的应用场景

案例一：产品质量检验

在制造业生产过程中，零部件的尺寸控制至关重要。例如，某机械零件的设计直径要求为 19.95, 20.05 mm。由于测量工具存在精度误差和操作误差，实际测得的尺寸常以区间形式表示，如 19.90, 20.10 mm。利用区间比较方法，可以判断实际测量区间是否完全包含于设计公差区间内，从而决定产品是否合格。若测量区间超出公差区间，则需判定该批产品存在超差风险。这种方式能有效规避因单点测量误差导致的误判，提高产品质量检验的可靠性。

案例二：项目投资评估

企业在进行投资决策时，往往需要面对未来市场环境不确定带来的收益波动。例如，某企业基于专家预测与市场数据，估计方案A未来三年年化收益率为 6%，而方案B为 8%。通过区间排序、支配度分析及可能度方法，可以系统性地比较两个方案的收益水平与风险状况。若企业风险承受能力较强，可优先选择区间上限较高的方案B；若风险偏好保守，则可进一步分析区间重叠度及稳健性，辅助科学、理性的投资选择。区间数方法有效弥补了传统单值预测忽略不确定性的问题。

案例三：环境监测分析

环境监测工作中，空气污染数据常受仪器误差、采样时间和气候因素影响，导致观测数据存在区间不确定性。例如，某区域PM2.5浓度记录为 35,45 μg/m³、40,50 μg/m³。通过计算区间均值、宽度及变化趋势，可评估空气质量的波动状况和污染风险等级。结合时间序列分析与区间趋势线方法，监测部门能动态掌握空气污染变化趋势，科学发布健康预警和治理措施。区间数方法提升了监测数据解释的灵活性和预警响应的科学性。

二、置信区间概述

在统计推断中，置信区间（Confidence Interval, CI）是一种用于估计总体参数范围的工具。它通过样本数据构建一个区间，使得该区间有一定的概率包含总体参数的真实值。置信区间的引入使得统计推断不仅仅依赖于一个点估计值，而是提供了一个更为全面的、能够反映不确定性的估计区间。在实际应用中，置信区间被广泛应用于各种领域，如医学、经济学、社会科学等，帮助决策者更好地理解和处理数据中的不确定性。

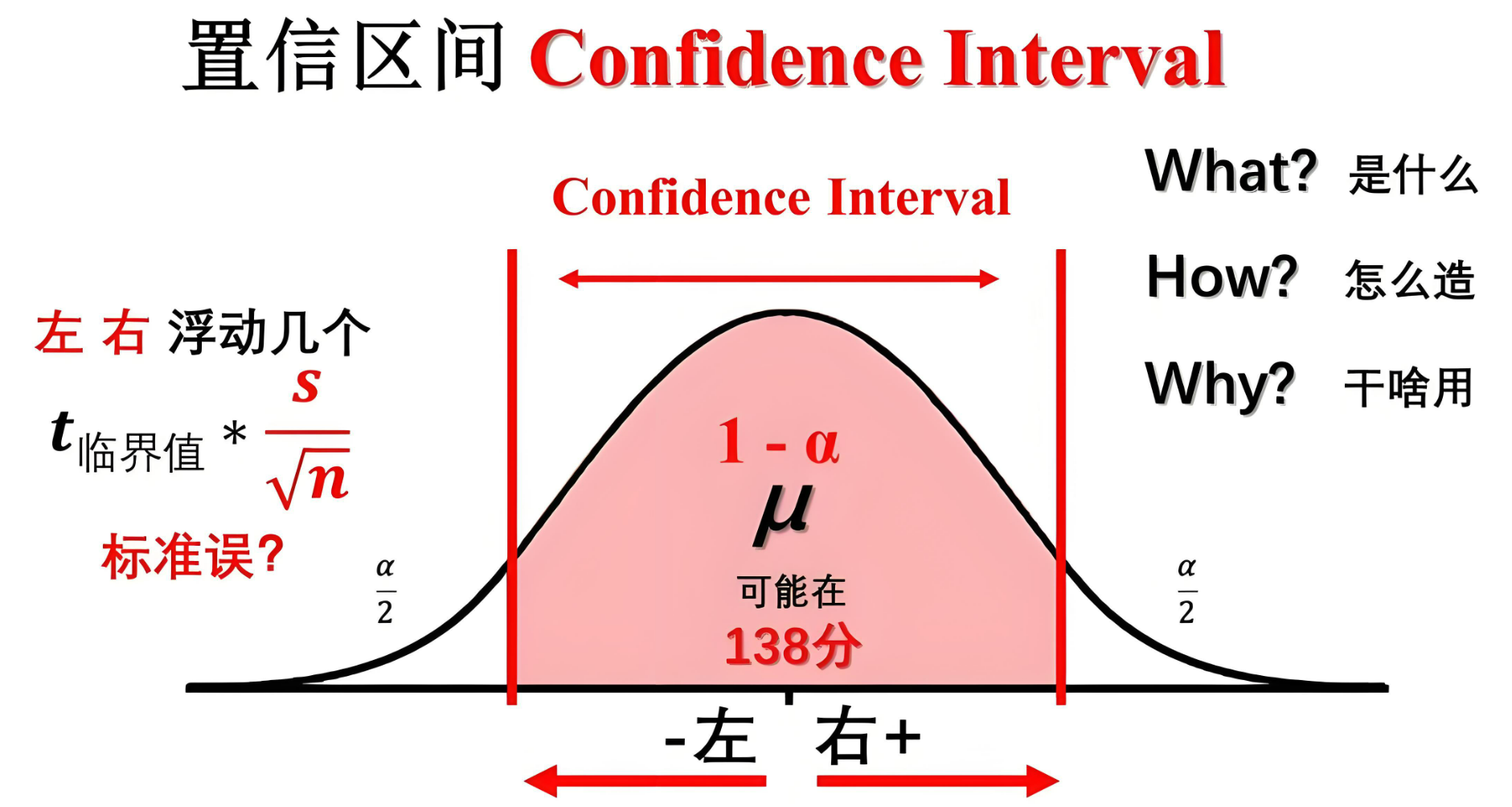
2.1 置信区间的结构

一个置信区间通常由两个部分组成：区间的下界和区间的上界，它们通过样本数据来估计。

• 下界与上界
  假设我们需要估计一个总体参数 \(\theta\)，通过样本统计量（如样本均值、样本比例等）对其进行估计。置信区间的形式通常为：

  \[[\hat{\theta} - E, \hat{\theta} + E] \]

  其中，\(\hat{\theta}\) 是样本估计值（如样本均值），而 \(E\) 是估计的误差，也称为误差边界（Margin of Error）。误差边界通常由标准误差（Standard Error）和一个临界值（如正态分布或t分布的分位数）共同决定。

• 误差边界的计算
  误差边界 \(E\) 反映了样本统计量对总体参数的估计误差。其计算公式为：

  \[E = z_{\alpha/2} \times \text{SE}(\hat{\theta}) \]

  其中，\(z_{\alpha/2}\) 是置信水平对应的分位数（例如，对于95%的置信水平，\(z_{\alpha/2} = 1.96\)，\(\text{SE}\hat{\theta}\) 是样本统计量的标准误差。标准误差反映了样本统计量的波动程度。

2.2 置信区间的术语

在置信区间的构建与解释中，有几个重要的术语需要掌握：

• 样本统计量（Sample Statistic）
  样本统计量是通过样本数据计算得到的值，它是总体参数的估计值。例如，样本均值 \(\bar{x}\) 和样本标准差 \(s\) 都是常见的样本统计量。

• 置信水平（Confidence Level）
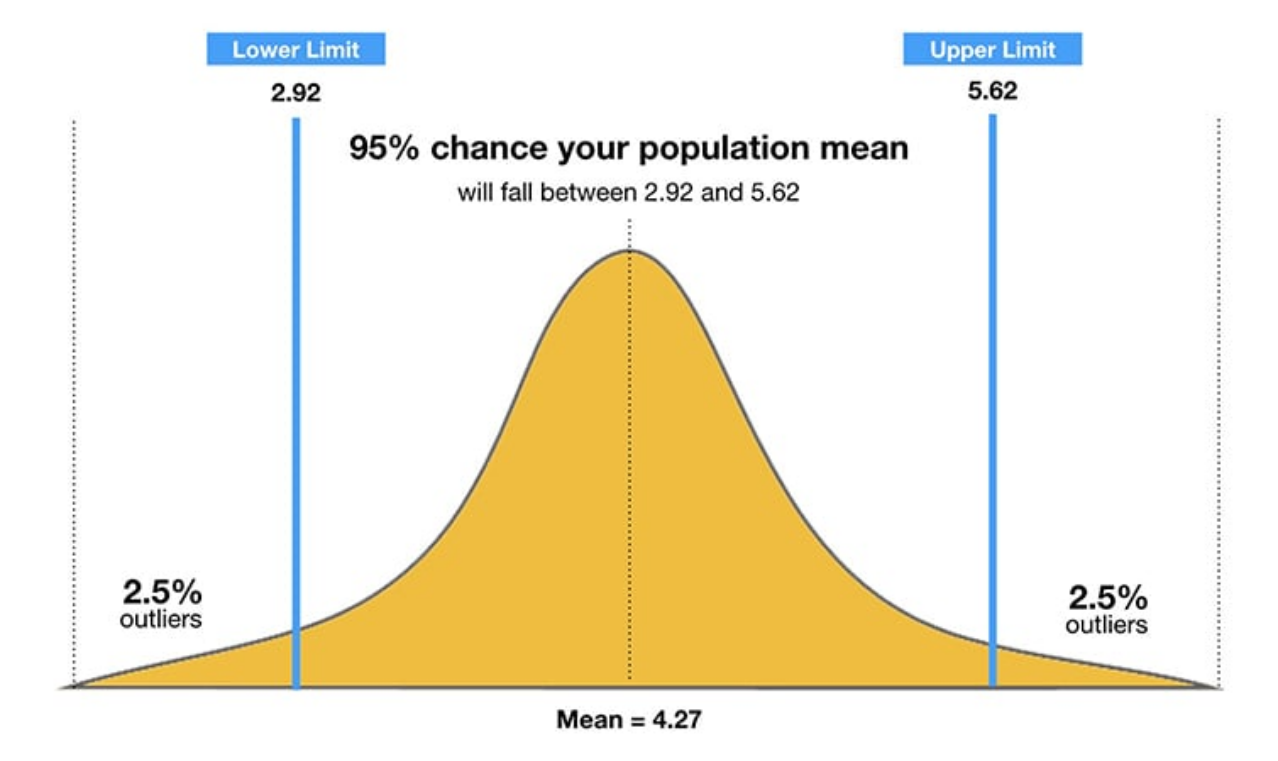
  置信水平是指置信区间包含真实总体参数的概率。常见的置信水平有90%、95%、99%等。例如，95%的置信区间意味着在重复的独立抽样中，约95%的样本所计算的置信区间会包含真实的总体参数。

• 临界值（Critical Value）
  临界值是由置信水平确定的常数。它通常是基于标准正态分布或\(t\)分布计算得到的分位数，用来调整样本估计值，以构建一个具有所需置信度的区间。对于95%的置信区间，通常使用1.96作为标准正态分布下的临界值。

• 标准误差（Standard Error）
  标准误差是样本统计量的标准偏差，它衡量了样本统计量的波动性。标准误差通常是通过样本数据的标准差与样本容量的平方根的比值来计算的。标准误差的大小直接影响置信区间的宽度。

• 置信区间的宽度（Confidence Interval Width）
  置信区间的宽度由误差边界 \(E\) 决定，误差边界越大，区间越宽，表示我们对参数估计的不确定性越大。相反，误差边界越小，置信区间越窄，表示我们对总体参数的估计更为精准。

2.3 置信区间的概率意义

置信区间的核心在于其概率意义，它反映了在重复抽样的情况下，所构建的区间包含真实总体参数的概率。

• 区间的解释
  例如，假设我们构建了一个95%的置信区间 \([L, U]\)，这个区间表示“我们有95%的信心认为，真实的总体参数值会落在这个区间内”。需要注意的是，置信区间的解释不是“总体参数落在区间内的概率为95%”，而是“如果我们重复抽取样本并计算置信区间，则约95%的区间会包含总体参数”。

• 置信区间的重复性
  置信区间的概率意义与抽样过程的重复性紧密相关。对于一个特定的样本，区间的真实包含概率是固定的，即“该区间要么包含真实参数，要么不包含”，这不是一个随机事件。区间的概率含义体现在“如果我们重复抽取样本，构建的95%置信区间中，约95%的区间会包含真实参数”。

• 置信水平与不确定性
  置信水平反映了我们对于区间包含真实参数的信心。在较低的置信水平下（如90%），置信区间会较窄，表示我们对参数的估计较为精确，但可靠性较低；而在较高的置信水平下（如99%），置信区间会较宽，表示我们对参数估计的可靠性更高，但估计值的精确度较低。

• 区间估计与点估计的关系
  置信区间提供了比点估计更丰富的信息。点估计仅给出一个单一值，而置信区间提供了一个值的区间，并且通过置信水平给出了该区间包含真实参数值的概率。点估计可以看作是置信区间宽度为零的特殊情况。

2.4 置信区间覆盖率模拟实验

区间估计是在点估计的基础上，利用样本统计量构建一个对称的置信区间，以区间形式估计总体参数。点估计值作为区间估计的中心值，一方面体现了样本统计量对总体参数的代表性，即样本提供的信息能够较好地反映总体特征；另一方面体现了正态分布普范性的特点，中心趋势是出现频数(概率)最多的值(点)。然而，单一的点估计无法反映估计过程中的不确定性，因为样本的随机性导致不同样本对应不同的估计值，存在一定误差。区间估计通过构建一个包含总体参数的区间，明确估计值的变动范围，将估计的不确定性以区间长度的形式表现出来，增强了结果的稳健性。此外，样本统计量本身是离散型随机变量，其取值随着样本的不同而波动，因此区间估计需结合统计量分布特性，合理调整区间宽度，反映估计的不确定性程度，三者共同构成了区间估计的基本结构，使其成为比点估计更全面、稳健且更具解释力的参数推断方法。

#30个置信区间模拟
import numpy as np
import matplotlib.pyplot as plt
import scipy.stats as stats

# 中文字体设置
plt.rcParams['font.sans-serif'] = ['SimHei']  
plt.rcParams['axes.unicode_minus'] = False  

# 参数设置
n = 30  # 样本容量
mu = 3   # 理论均值
sigma = 4  # 理论标准差
times = 30  # 样本次数
alpha = 0.05  # 置信度为95%

# 存储结果
means = []
lower = []
upper = []
cover = []

# 计算每个样本的置信区间，判断是否包含理论均值3
for i in range(times):
    sample_data = np.random.normal(mu, sigma, n)  # 生成样本数据
    sample_mean = np.mean(sample_data)  # 样本均值
    se = np.std(sample_data, ddof=1) / np.sqrt(n)  # 样本标准误
    z = stats.norm.ppf(1 - alpha/2)  # z值，基于标准正态分布
    
    # 计算该样本均值的置信区间
    ci_lower = sample_mean - z * se
    ci_upper = sample_mean + z * se
    
    # 判断置信区间是否包含理论均值3
    cover.append(ci_lower <= mu <= ci_upper)
    
    # 存储每个样本的均值及其置信区间
    means.append(sample_mean)
    lower.append(ci_lower)
    upper.append(ci_upper)

# 计算包含3的比例
cover_ratio = np.mean(cover)
print(f"包含理论均值3的比例: {cover_ratio:.3f}")

# 绘图
plt.figure(figsize=(12, 6))

# 绘制置信区间图
for i in range(times):
    # 画置信区间竖线（蓝色）
    plt.plot([i+1, i+1], [lower[i], upper[i]], color='blue', linewidth=2)
    
    # 上下限黄色大点（size=60）
    plt.scatter(i+1, lower[i], color='gold', s=60)
    plt.scatter(i+1, upper[i], color='gold', s=60)
    
    # 判断区间是否包含理论均值3，点颜色和大小
    if cover[i]:
        # 覆盖 — 红色小点（size=30）
        plt.scatter(i+1, means[i], color='red', s=30)
    else:
        # 不覆盖 — 黑色大点（size=60）
        plt.scatter(i+1, means[i], color='black', s=60)

# 总体均值水平线（理论均值3）
plt.axhline(y=mu, color='green', linestyle='dashed', label='理论均值 μ=3')

# 绘制点估计的连线图
plt.plot(range(1, times+1), means, color='purple', marker='o', markersize=6, label='点估计值连线')

# 坐标轴和图例
plt.xlabel('样本编号')
plt.ylabel('样本均值及其置信区间')
plt.title('30个样本均值及其95%置信区间（每个点估计的置信区间）与点估计连线')
plt.legend()
plt.grid(True)
plt.tight_layout()
plt.show()

点估计(点估计的变化更适宜用区间数表达)	置信区间

#50个置信区间模拟
import numpy as np
import matplotlib.pyplot as plt
import scipy.stats as stats

# 中文字体设置
plt.rcParams['font.sans-serif'] = ['SimHei']  
plt.rcParams['axes.unicode_minus'] = False  

# 参数设置
n = 30  # 样本容量
mu = 3   # 理论均值
sigma = 4  # 理论标准差
times = 50  # 样本次数
alpha = 0.05  # 置信度为95%

# 存储结果
means = []
lower = []
upper = []
cover = []

# 计算每个样本的置信区间，判断是否包含理论均值3
for i in range(times):
    sample_data = np.random.normal(mu, sigma, n)  # 生成样本数据
    sample_mean = np.mean(sample_data)  # 样本均值
    se = np.std(sample_data, ddof=1) / np.sqrt(n)  # 样本标准误
    z = stats.norm.ppf(1 - alpha/2)  # z值，基于标准正态分布
    
    # 计算该样本均值的置信区间
    ci_lower = sample_mean - z * se
    ci_upper = sample_mean + z * se
    
    # 判断置信区间是否包含理论均值3
    cover.append(ci_lower <= mu <= ci_upper)
    
    # 存储每个样本的均值及其置信区间
    means.append(sample_mean)
    lower.append(ci_lower)
    upper.append(ci_upper)

# 计算包含3的比例
cover_ratio = np.mean(cover)
print(f"包含理论均值3的比例: {cover_ratio:.3f}")

# 绘图
plt.figure(figsize=(12, 6))

for i in range(times):
    # 画置信区间竖线（蓝色）
    plt.plot([i+1, i+1], [lower[i], upper[i]], color='blue', linewidth=2)
    
    # 上下限黄色大点（size=60）
    plt.scatter(i+1, lower[i], color='gold', s=60)
    plt.scatter(i+1, upper[i], color='gold', s=60)
    
    # 判断区间是否包含理论均值3，点颜色和大小
    if cover[i]:
        # 覆盖 — 红色小点（size=30）
        plt.scatter(i+1, means[i], color='red', s=30)
    else:
        # 不覆盖 — 黑色大点（size=60）
        plt.scatter(i+1, means[i], color='black', s=60)

# 总体均值水平线（理论均值3）
plt.axhline(y=mu, color='green', linestyle='dashed', label='理论均值 μ=3')

# 坐标轴和图例
plt.xlabel('样本编号')
plt.ylabel('样本均值及其置信区间')
plt.title('50个样本均值及其95%置信区间（每个点估计的置信区间）')
plt.legend()
plt.grid(True)
plt.tight_layout()
plt.show()

2.5 置信区间的应用

置信区间不仅在理论研究中有重要作用，还在实际数据分析中得到了广泛应用：

• 科学研究与数据分析
  置信区间是许多科学研究中数据分析的重要工具，它使得研究者能够量化实验结果中的不确定性。例如，在药物效果研究中，通过计算置信区间来判断药物是否对患者的治疗有显著影响。

• 经济学与政策分析
  经济学中，很多模型的参数都是通过样本数据进行估计的。置信区间可以帮助经济学家了解政策变化对经济变量的潜在影响，并量化政策效果的不确定性。

• 质量控制
  在质量管理中，置信区间被用来评估生产过程中产品质量的稳定性和一致性。通过构建置信区间，可以判断生产过程是否处于可控状态。

置信区间是统计推断中的一个重要概念，它通过样本数据估计总体参数的范围，并为区间赋予置信度，从而提供了一个更为可靠的估计方法。置信区间的概率意义和置信水平的选择，使其在实际数据分析中能够帮助我们理解结果的不确定性，辅助决策和判断。通过对置信区间的深入理解，能够在不同领域中更好地应用这一工具，提升数据分析的科学性和可靠性。

三、区间估计的区间数视角理解

在统计推断中，参数估计方法主要分为两类：点估计和区间估计。点估计是用一个单一的数值来估计总体参数，比如用样本均值去估计总体均值。虽然点估计计算简便，但由于样本容量有限、数据波动、抽样误差等因素，点估计往往不能准确反映总体的真实情况。因此，区间估计方法应运而生。区间估计（Interval Estimation）是指在给定置信度下，利用样本信息对总体参数确定一个上、下界区间，称为置信区间，表示总体参数落在该区间内的可能性。这种方法克服了点估计的局限，能够更全面地反映参数估计中的不确定性和抽样波动情况。
如果我们从区间数（Interval Number）的数学视角重新审视区间估计，会发现区间估计本质上就是一种“带概率含义的区间数表达形式”。它不仅有一个确定的取值区间，还有明确的概率属性。这种结合为不确定性建模和数据解释提供了更严谨和直观的方式。

3.1 区间数与区间估计的基本形式

在数学中，区间数通常表示为：

\[A = [a^-, a^+] \]

其中，$ a^- $ 是区间下界，$ a^+ $ 是区间上界。区间数用于描述变量在一个确定范围内取值的不确定性。这种不确定性源于测量误差、数据波动、环境影响或估计方法局限，但区间本身没有概率属性，只是表示“值可能落在该区间之内”。

而在统计区间估计中，一个总体参数 $ \theta $ 的置信区间表示为：

\[[\hat{\theta}_L, \hat{\theta}_U] \]

其中，$ \hat{\theta}_L $ 和 $ \hat{\theta}_U $ 分别是根据样本数据、抽样分布及指定置信度计算得到的区间下界和上界。这个区间不同于一般的区间数，因为它具有统计意义上的概率属性。例如，当置信度为95%时，意味着“在相同抽样方法下，95%的样本所计算得到的区间将覆盖总体参数值”。

形式上，两者同为一个闭区间，反映数值在某个范围内的不确定性。不同之处在于，区间估计为区间赋予了置信度，即覆盖总体参数的概率，构成了“带概率的区间数”。

3.2 区间估计的“带概率区间数”特性

我们可以将区间估计理解为一种特殊的区间数，这种区间数不仅描述某个变量的不确定范围，还结合概率理论，表征区间包含真实值的可能性。
其本质特征包括：

• 区间存在上下界 区间估计的结果总是一个闭区间，形式上与区间数相同，表示某个参数的不确定范围。
• 区间由样本信息确定 区间估计的上下界根据样本统计量、抽样分布以及置信度计算得出，反映样本信息对总体参数的估计能力。
• 区间具备置信度属性 与普通区间数不同，区间估计的区间包含了一个概率意义，即“该区间覆盖真实参数值的可能性达到置信度水平（如95%、99%）”。
• 区间宽度反映不确定性大小 区间越宽，说明估计不确定性越大，区间越窄，说明估计值越稳定、可靠。

3.3 区间数视角下区间估计的意义

从区间数的角度看，区间估计不仅是一种统计推断方法，更是一种严谨的数值不确定性建模方式。其意义体现在以下几个方面：

① 反映抽样误差与不确定性

由于样本信息有限，总体参数值往往无法被单点估计准确反映。区间估计通过区间数形式，将总体参数值限定在一个上下界之内，用区间长度体现估计误差大小。这种方式兼顾了中心估计值及其变动范围，能够客观反映统计推断的不确定性。

② 量化估计可靠性

区间估计赋予区间以置信度这一概率含义，直观反映区间包含总体参数的可靠程度。例如，95%置信区间表示在相同条件下重复抽样，95%的区间将覆盖总体参数。这种带概率的区间数形式，为估计结果增添了可解释性和可信度。

③ 辅助科学决策

在实际应用中，区间估计结果能够为风险评估、质量控制、经济决策等提供依据。相比单点估计，区间估计反映了估计值的可靠区间，帮助决策者充分考虑潜在误差和不确定性，作出更加稳健、科学的判断。

④ 提升不确定性建模能力

现实问题中，由于数据不完整、环境复杂、样本偏差等原因，很多结论无法以单点形式表达。区间估计通过区间数方式，全面反映估计区间及其置信度，使不确定性表达更符合实际情况，特别适合小样本、高波动性、复杂环境下的推断分析。

举例说明

以总体均值估计为例，假设我们抽取了100个样本，计算样本均值为50，标准差为10。若要构造95%置信区间，可以用正态分布方法：

\[\left( \bar{x} - z_{\alpha/2} \frac{s}{\sqrt{n}}, \bar{x} + z_{\alpha/2} \frac{s}{\sqrt{n}} \right) \]

代入具体数值：

\[50 \pm 1.96 \times \frac{10}{\sqrt{100}} = [48.04, 51.96] \]

这个区间即为带有95%置信度的区间估计，既是一个区间数 \([48.04, 51.96]\)，又是一个覆盖总体均值的“带概率的区间数”，其区间宽度反映抽样误差，置信度95%反映估计可靠性。

📊 总结与思考

区间估计可以理解为带概率属性的区间数形式，它利用样本数据和概率理论来构建一个上下界的区间，进而描述总体参数的可能取值范围，并赋予该区间一定的置信度。这种方式不仅比单点估计提供了更丰富的信息，也能够更准确地反映数据中的不确定性和抽样误差，从而为决策者提供更可靠的依据。通过区间估计，我们不仅得到一个估计值，而是得到一个具有置信度的区间，这使得我们的推断更加全面和科学。
与单点估计相比，区间估计能够有效处理和量化不确定性，避免了简单估计可能带来的偏差和误导。在实际应用中，区间估计已成为许多领域（如医学研究、经济预测、质量控制等）的标准工具，帮助专业人士更好地理解数据背后的潜在变动和不确定性。从数学角度来看，区间估计与区间数的本质非常相似，都通过区间的形式描述不确定性。然而，区间估计更加依赖于概率统计的框架，具有概率化、统计化的特点。这不仅使得区间估计具备更高的精确度和可信度，也赋予它更强的实用性。通过这种区间描述方法，统计学能够更灵活地进行推断，从而为实际问题提供更加切合的解决方案。

📁 参考文献

1. 区间数排序方法综述
2. 区间数计算之Python实现
3. 点估计和区间估计——统计学概念

#30个置信区间模拟
# 加载库
library(ggplot2)
library(showtext)

# 中文字体设置
showtext_auto()
font_add("SimHei", regular = "simhei.ttf")  # 确保有simhei.ttf，或改为本地支持的中文字体
theme_set(theme_gray(base_family = "SimHei"))

# 设置参数
set.seed(123)
n <- 30        # 样本容量
mu <- 3        # 理论均值
sigma <- 4     # 理论标准差
times <- 30    # 样本次数
alpha <- 0.05  # 置信度95%

# 存储结果
means <- numeric(times)
lower <- numeric(times)
upper <- numeric(times)
cover <- logical(times)

# 计算每组样本的均值和置信区间
for (i in 1:times) {
  sample_data <- rnorm(n, mean = mu, sd = sigma)
  sample_mean <- mean(sample_data)
  se <- sd(sample_data) / sqrt(n)
  z <- qnorm(1 - alpha/2)
  
  ci_lower <- sample_mean - z * se
  ci_upper <- sample_mean + z * se
  
  cover[i] <- (ci_lower <= mu & mu <= ci_upper)
  
  means[i] <- sample_mean
  lower[i] <- ci_lower
  upper[i] <- ci_upper
}

# 计算包含3的比例
cover_ratio <- mean(cover)
cat(sprintf("包含理论均值3的比例: %.3f\n", cover_ratio))

# 整理数据框
df <- data.frame(
  id = 1:times,
  mean = means,
  lower = lower,
  upper = upper,
  cover = cover
)

# 画图
ggplot(df, aes(x = id)) +
  # 置信区间蓝色竖线
  geom_segment(aes(y = lower, yend = upper, xend = id), color = "blue", linewidth = 1.2) +
  # 上下限黄色大点
  geom_point(aes(y = lower), color = "gold", size = 3) +
  geom_point(aes(y = upper), color = "gold", size = 3) +
  # 覆盖情况点：红色小点/黑色大点
  geom_point(aes(y = mean, color = cover, size = cover)) +
  scale_color_manual(values = c("black", "red")) +
  scale_size_manual(values = c(4, 2)) +
  # 点估计连线图
  geom_line(aes(y = mean), color = "purple", linewidth = 1) +
  # 理论均值水平线
  geom_hline(yintercept = mu, linetype = "dashed", color = "green") +
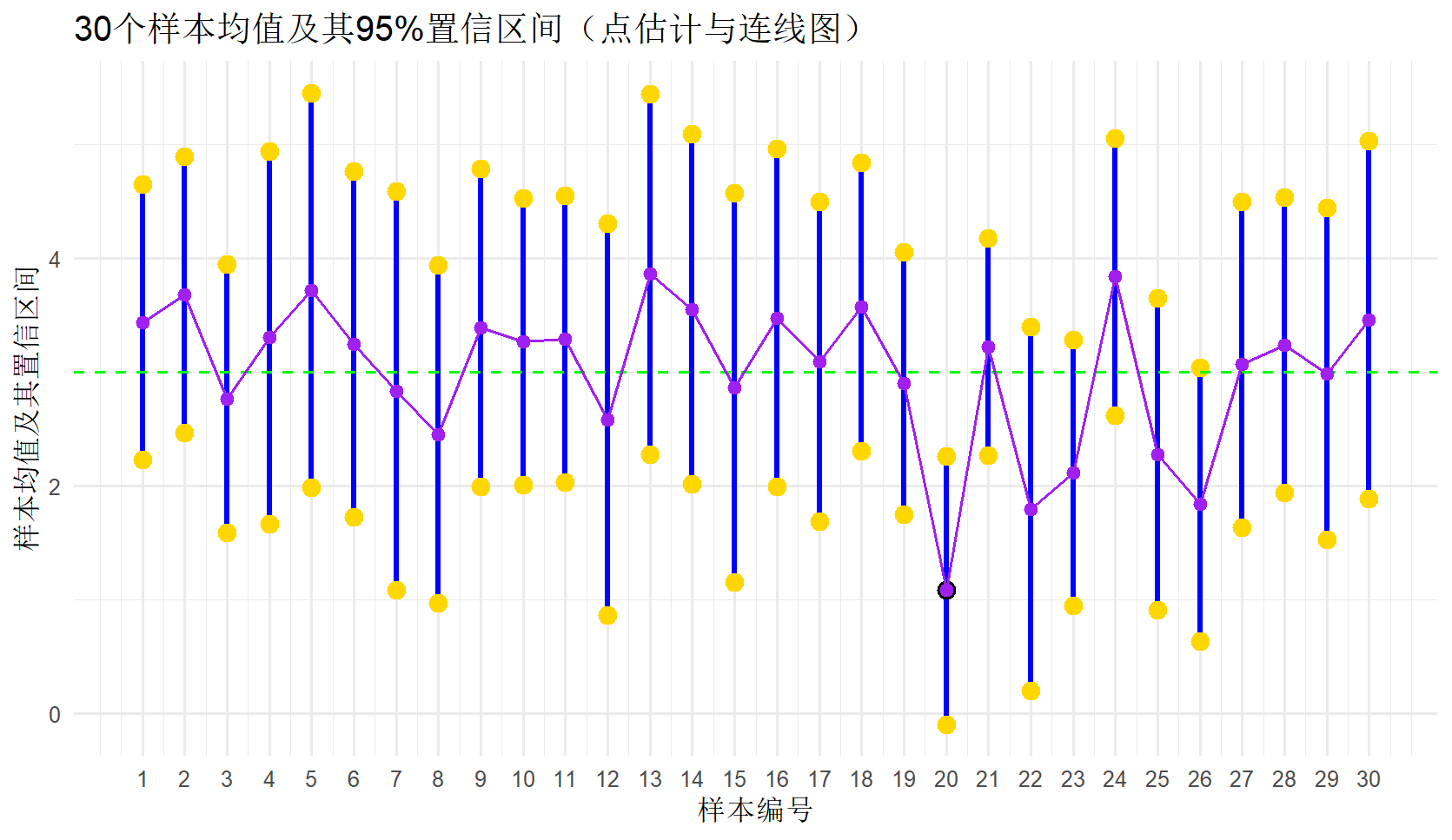
  labs(title = "30个样本均值及其95%置信区间与点估计连线",
       x = "样本编号", y = "样本均值及其置信区间") +
  theme_minimal(base_family = "SimHei") +
  theme(legend.position = "none") +
  scale_x_continuous(breaks = 1:times)

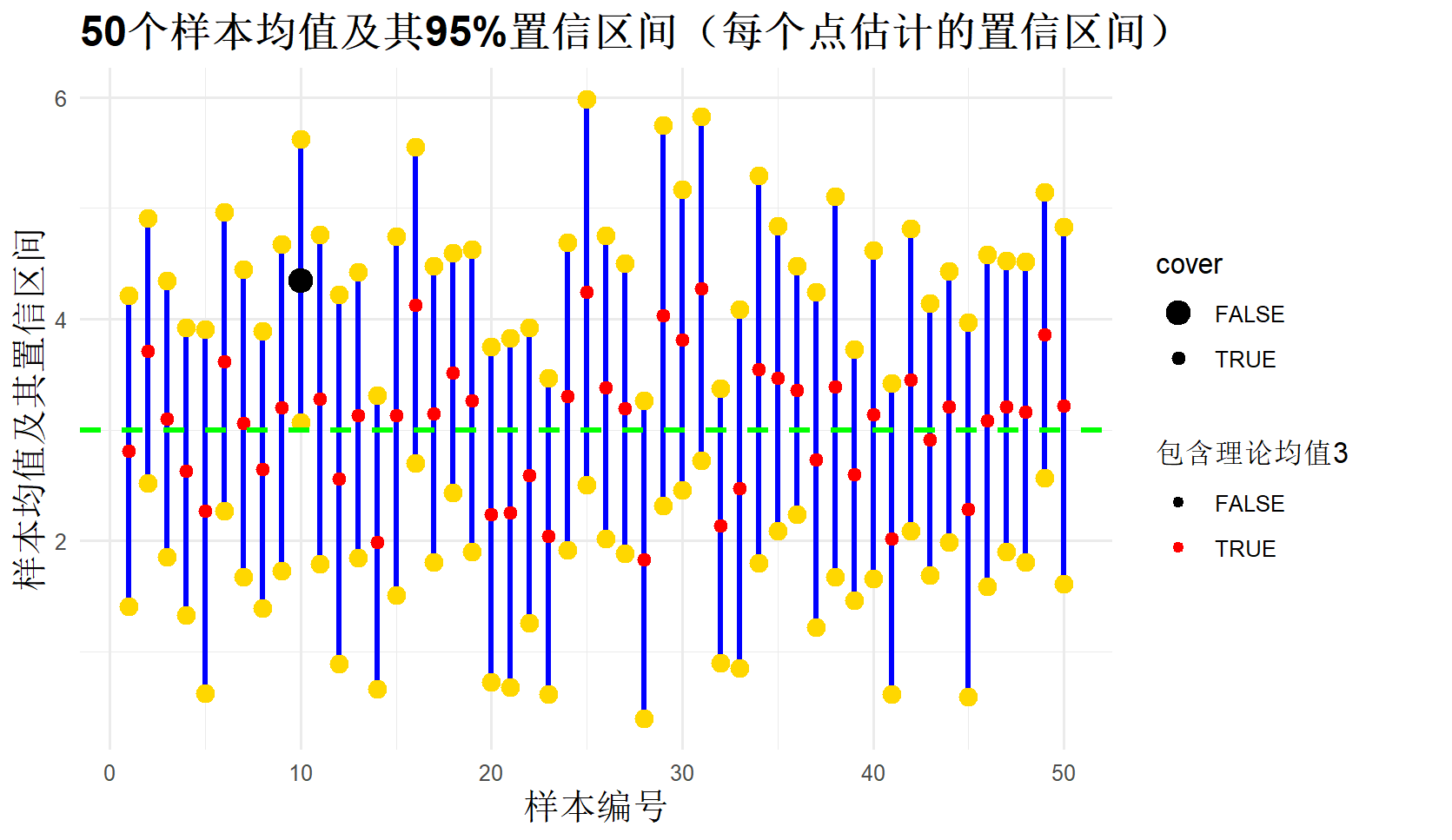
点估计	置信区间

#50个置信区间模拟
# 加载所需包
library(ggplot2)

# 参数设置
n <- 30         # 样本容量
mu <- 3         # 理论均值
sigma <- 4      # 理论标准差
times <- 50     # 样本次数
alpha <- 0.05   # 置信度为95%

# 存储结果
means <- numeric(times)
lower <- numeric(times)
upper <- numeric(times)
cover <- logical(times)

# 计算每个样本的置信区间，判断是否包含理论均值3
set.seed(123)  # 保证可重复
for (i in 1:times) {
  sample_data <- rnorm(n, mean=mu, sd=sigma)   # 生成样本数据
  sample_mean <- mean(sample_data)             # 样本均值
  se <- sd(sample_data) / sqrt(n)              # 样本标准误
  z <- qnorm(1 - alpha/2)                      # z值，基于标准正态分布
  
  # 计算该样本均值的置信区间
  ci_lower <- sample_mean - z * se
  ci_upper <- sample_mean + z * se
  
  # 判断置信区间是否包含理论均值3
  cover[i] <- (ci_lower <= mu & mu <= ci_upper)
  
  # 存储结果
  means[i] <- sample_mean
  lower[i] <- ci_lower
  upper[i] <- ci_upper
}

# 计算包含3的比例
cover_ratio <- mean(cover)
cat(sprintf("包含理论均值3的比例: %.3f\n", cover_ratio))

# 整理成数据框
df <- data.frame(
  id = 1:times,
  mean = means,
  lower = lower,
  upper = upper,
  cover = cover
)

# 画图
ggplot(df, aes(x = id, y = mean)) +
  # 绘制置信区间线段
  geom_errorbar(aes(ymin = lower, ymax = upper), color = "blue", width = 0.2, size = 1) +
  # 上下限黄色点
  geom_point(aes(y = lower), color = "gold", size = 3) +
  geom_point(aes(y = upper), color = "gold", size = 3) +
  # 样本均值点，按是否覆盖颜色区分
  geom_point(aes(color = cover, size = cover)) +
  scale_color_manual(values = c("FALSE" = "black", "TRUE" = "red")) +
  scale_size_manual(values = c("FALSE" = 4, "TRUE" = 2)) +
  # 理论均值水平线
  geom_hline(yintercept = mu, linetype = "dashed", color = "green", size = 1) +
  # 坐标轴、标题和主题设置
  labs(
    x = "样本编号",
    y = "样本均值及其置信区间",
    title = "50个样本均值及其95%置信区间（每个点估计的置信区间）",
    color = "包含理论均值3"
  ) +
  theme_minimal(base_family = "SimHei") +   # 中文字体
  theme(
    plot.title = element_text(size = 16, face = "bold"),
    axis.title = element_text(size = 14)
  )