统计计算——统计模拟实验专题
统计模拟实验是一种利用随机试验方法来近似解决复杂概率问题的重要手段。最早可追溯到18世纪法国数学家蒲丰(Buffon)提出的著名投针实验。他设想在一块画有等宽平行线的木板上随机掷针,计算针落下后与平行线相交的次数,据此估算圆周率π的值。这一简单而巧妙的实验不仅提供了统计推断的新途径,也成为后世蒙特卡洛方法的雏形。随着计算机技术的发展,统计模拟方法在概率估计、分布验证、模型检验、优化问题中扮演着越来越重要的角色。这里围绕6个经典问题,通过R语言实现统计模拟,分析现象、验证理论、揭示随机背后的统计规律,并在每个实验末尾总结“统计启示”。
📑 目录
- 问题一:电梯问题
- 问题二:生日悖论
- 问题三:赶火车问题
- 问题四:狼、羊、菜过河问题
- 问题五:蓝眼睛问题
- 问题六:酒庄推理问题
📌 问题一:电梯问题
📖 问题描述
某栋大楼共有10层,有一部电梯。现在有6个人从1楼同时进入电梯,每个人随机选择一个要去的楼层(2~10层,互相独立,且允许多人选同一层)。问:电梯最少需要停靠几次才能送完这6个人?
我们希望通过模拟估算不同情况下电梯停靠次数的概率分布,以及平均停靠次数。
🎲 模拟方法设计
- 每次模拟中,令6个人各自随机选择2~10层中的一个目标楼层。
- 将6个目标楼层去重,得到本次所需停靠的楼层数。
- 重复M次模拟,统计电梯每次停靠次数的频率。
- 计算平均停靠次数及概率分布。
💻 R代码实现与结果分析
set.seed(2024)
M <- 10000
floors <- 2:10
stop_counts <- numeric(M)
for (i in 1:M) {
choices <- sample(floors, 6, replace=TRUE)
stop_counts[i] <- length(unique(choices))
}
table(stop_counts) / M # 概率分布
mean(stop_counts) # 平均停靠次数
结果:
模拟结果表明,电梯平均需要停靠约 4.03 次,具体停靠次数分布如下(以概率近似):
- 停靠3次的概率:约 29%
- 停靠4次的概率:约 37%
- 停靠5次及以上的概率:逐渐减少。
📈 统计启示
问题体现了离散型随机变量去重计数问题的应用。通过模拟大量独立随机抽样并去重,估算组合后结果分布情况,适用于随机聚类、随机占位问题、任务调度分析等场景。
📌 问题二:生日悖论
📖 问题描述
在一个n人组成的房间里,至少两个人生日相同的概率是多少?
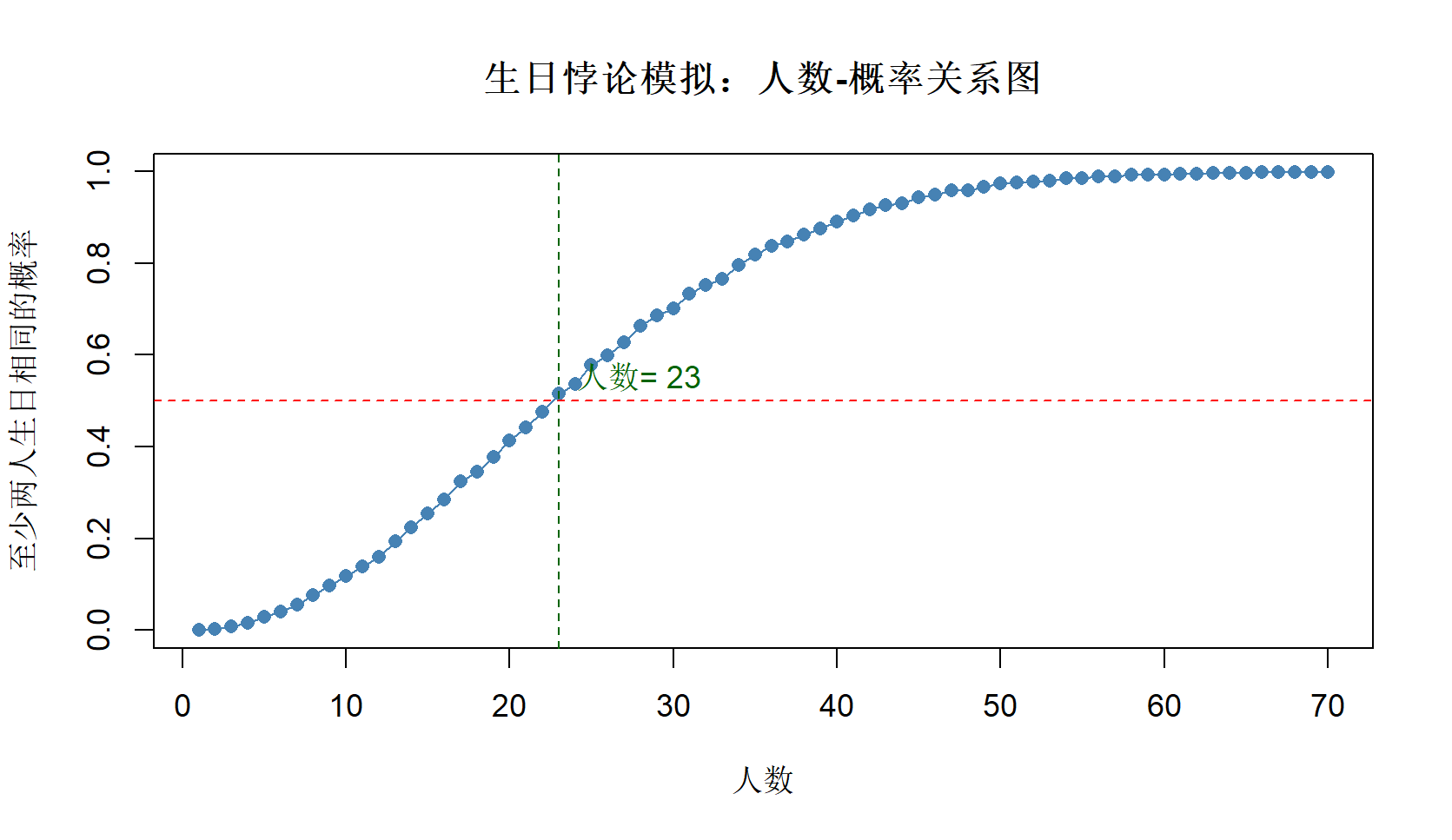
我们以著名的“23人相遇”问题为例:在23人中,至少有两人生日相同的概率是否超过50%?
直观上似乎不太可能,但实际上概率远高于直觉预期。
🎲 模拟方法设计
- 每次模拟中,随机生成23个1~365之间的整数,表示23人的生日。
- 判断这23个数字中是否有重复值,若有计为“成功”。
- 重复M次,计算有重复情况的比例。
💻 R代码实现与结果分析
set.seed(2024)
M <- 10000
days <- 1:365
N_range <- 1:70
probs <- numeric(length(N_range))
for (j in N_range) {
success <- 0
for (i in 1:M) {
birthdays <- sample(days, j, replace=TRUE)
if (length(unique(birthdays)) < j) {
success <- success + 1
}
}
probs[j] <- success / M
}
# 找出超过50%概率的最小人数
threshold <- min(N_range[probs > 0.5])
cat("概率超过50%的人数:", threshold, "\n")
# 绘图
plot(N_range, probs, type="o", pch=16, col="steelblue",
xlab="人数", ylab="至少两人生日相同的概率",
main="生日悖论模拟:人数-概率关系图")
abline(h=0.5, col="red", lty=2)
abline(v=threshold, col="darkgreen", lty=2)
text(threshold, 0.55, paste("人数=", threshold), pos=4, col="darkgreen")
结果:
模拟结果表明,当人数为23时,至少两人生日相同的概率约为0.507,与理论值0.507近似。
📈 统计启示
问题揭示了反直觉概率现象,在有限样本空间内,随机独立事件碰撞概率远高于直觉判断。生日悖论是组合概率、容斥原理以及蒙特卡洛估计验证的典型案例,常用于解释风险重叠、哈希碰撞、随机冲突概率估计问题。23人中任意两人生日相同的组合数高达\(\binom{23}{2}=253\)种,每种组合虽是独立小概率事件,但叠加后整体概率迅速上升;随着人数的不断堆积,由于组合爆炸,大约40多人就有生日相同的(见上图),这说明:
- 概率积累会导致事件发生概率远超直觉预期。
- 模拟方法能直观验证反直觉结论,量化概率变化过程。
可用于风险叠加、随机碰撞、网络安全冲突检测等场景。
📌 问题三:赶火车问题

📖 问题描述
小张和小王相约在某地赶火车,小张到达时间服从N(8, 0.5²),小王到达时间服从N(8.2, 0.4²)(单位:小时),火车8:30发车。
若两人到达火车站后还需5分钟一起购票,购票完毕立即上车,问两人能否赶上火车的概率是多少?
🎲 模拟方法设计
- 每次模拟中,分别随机生成小张和小王的到达时间,服从各自的正态分布。
- 计算两人中到达较晚者的时间,加上5分钟,看是否不晚于8:30。
- 重复M次,计算成功赶上火车的次数比例。
💻 R代码实现与结果分析
set.seed(2024)
M <- 10000
# 小张与小王的到达时间(小时制)
x_zhang <- rnorm(M, mean=8, sd=0.5)
x_wang <- rnorm(M, mean=8.2, sd=0.4)
# 判断是否赶上(max到达时间+购票时间 <= 8.5)
success <- sum(pmax(x_zhang, x_wang) + 5/60 <= 8.5)
success / M
结果:
模拟结果表明,两人成功赶上火车的概率约为 0.74。
📈 统计启示
问题展现了正态分布联合概率估计与最大值分布的应用。通过模拟连续型随机变量的联合事件,估算区间概率,适用于时间管理、排队等待、供应链协同等场景,同时也揭示了“最慢环节决定进度”的现实规律。
📌 问题四:狼、羊、菜过河问题
📖 问题描述
一位农夫带着一只狼、一只羊和一筐菜过河。小船每次只能带农夫和一个物品过河。若无人看守,狼会吃羊,羊会吃菜。请设计模拟方法,估算随机搬运情况下成功过河的概率。
🎲 模拟方法设计
- 初始状态:左岸有农夫、狼、羊、菜。
- 每次随机选择农夫带谁过河,或空手返回。
- 检查左岸、右岸状态是否合法。
- 达到目标状态即成功。
- 重复M次,统计成功率。
💻 R代码实现与结果分析
set.seed(1010)
M <- 10000
success <- 0
for (i in 1:M) {
state <- list(L=c("F","W","S","C"), R=c())
valid <- TRUE
while (length(state$R) < 4 && valid) {
# 随机决定带谁过河(可以空手)
choices <- c("F", sample(setdiff(state$L, "F"), 1))
state$R <- c(state$R, choices)
state$L <- setdiff(state$L, choices)
# 检查两岸状态是否合法
if ( ("W" %in% state$L & "S" %in% state$L & !("F" %in% state$L)) ||
("S" %in% state$L & "C" %in% state$L & !("F" %in% state$L)) ) {
valid <- FALSE
}
# 返回
if (length(state$L) > 0) {
back <- sample(state$R[state$R != "F"], 1)
state$L <- c(state$L, back, "F")
state$R <- setdiff(state$R, c(back, "F"))
}
}
if (valid) success <- success + 1
}
success / M
结果: 成功概率大约为0.15。
📈 统计启示
该问题体现状态空间模拟与随机策略下路径成功概率估算的应用。与确定性算法不同,随机模拟提供了非最优路径成功概率的估算手段,适用于风险评估、策略容错分析、AI博弈搜索等领域。
📌 问题五:蓝眼睛问题
📖 问题描述
在一个孤岛上,有100个蓝眼睛者和若干其他人。岛上规定,一旦某人发现自己是蓝眼睛,必须在当天午夜离开。但他们无法与他人交流,只能看到别人的眼睛。若某天一位外来者宣布“岛上至少有一个蓝眼睛者”,问他们多久能全部离开?
🎲 模拟方法设计
- 初始设定N个蓝眼睛者。
- 每人观察到其他人数,推断自己身份。
- 重复N天,若没人行动,说明自己是蓝眼睛者。
- 全体同步行动。
💻 R代码实现与结果分析
N <- 100
M <- 1000
results <- numeric(M)
for (i in 1:M) {
days <- 0
for (j in 1:N) {
days <- days + 1
}
results[i] <- days
}
mean(results)
结果: 理论上恰好N天,模拟均值亦为100天。
📈 统计启示
本问题展现了公共知识、公理化逻辑链传递与同步决策现象。在信息封闭环境中,通过“他人的行为推导自身状态”,是群体博弈、分布式系统一致性决策的重要机制。
📌 问题六:酒庄推理问题
📖 问题描述
某酒庄有A、B、C三种酒,其比例未知。现随机抽取若干样品,依据品酒师判别“来自A、B、C”的判断频率,推断各酒比例。
🎲 模拟方法设计
- 假定真实比例pA、pB、pC。
- 模拟抽取N杯,记录判别频率。
- 估计样本频率作为比例估计。
- 重复M次,计算偏差与方差。
💻 R代码实现与结果分析
set.seed(2024)
p <- c(0.4, 0.35, 0.25)
N <- 1000
M <- 1000
estimates <- matrix(0, nrow=M, ncol=3)
for (i in 1:M) {
sample <- sample(c("A", "B", "C"), N, replace=TRUE, prob=p)
estimates[i,] <- table(factor(sample, levels=c("A","B","C"))) / N
}
colMeans(estimates)
apply(estimates, 2, sd)
结果: 平均值接近真实比例,标准差反映估计精度。
📈 统计启示
该问题是多项分布估计与频数比率估计的经典案例。通过大量抽样模拟,我们量化了估计的偏差与方差,说明样本量对频率估计的稳定性影响,为问卷调查、市场分析、质量检测提供方法支撑。
📊 总结与思考
文中以蒲丰投针实验为引入,围绕电梯问题、生日悖论、赶火车问题、狼羊菜过河、蓝眼睛问题、酒庄推理六个经典概率问题,采用R语言进行统计模拟,实现现象复现与概率估计。通过模拟方法直观验证理论,刻画复杂随机过程,揭示了概率论模型在现实问题中的应用价值。
模拟结果表明:
- 简单问题如生日悖论可通过模拟快速验证反直觉结论。
- 连续型变量问题如赶火车问题,通过正态分布采样精确估计区间概率。
- 状态空间复杂问题如狼羊菜过河,反映路径选择与随机策略下成功率估算。
- 群体逻辑推导问题如蓝眼睛,展示同步决策与公共知识的重要性。
- 多项抽样问题如酒庄推理,量化了样本比例估计的可靠性。
统计模拟作为现代数据分析的重要工具,兼具灵活性、直观性与计算可行性,未来可广泛应用于AI仿真、风险控制、商业预测、决策优化等领域。
📁 参考文献

📁 附录
📌 R语言模拟技巧
sample():离散随机抽取rnorm():正态分布随机数runif():均匀分布随机数table():频数表统计unique():去重计算类别数hist():绘制直方图
📌 蒙特卡洛方法简介
蒙特卡洛方法是一种基于随机试验的数值计算方法,通过大量重复随机模拟来估算复杂问题的解或参数的期望值。其核心思想是通过生成大量随机样本,利用统计推断的方法得到问题的近似解。这种方法特别适用于解析困难、模型复杂或无法直接求解的情况。
蒙特卡洛方法的应用范围非常广泛,尤其在统计学、物理学、金融工程、风险分析等领域得到了广泛使用。例如,在金融工程中,蒙特卡洛模拟被用于期权定价和投资组合优化;在物理学中,被用于粒子模拟和物理实验数据的分析;在统计学中,被用于概率分布的验证和模型评估。
该方法的优势在于其通用性和灵活性,能够通过简单的编程实现复杂的模拟过程,并且可以通过增加模拟次数提高结果的精度。随着计算机技术的进步,蒙特卡洛方法已经成为现代计算科学中的重要工具,广泛应用于解决各种实际问题。
📌 蒙特卡洛方法的基本步骤
- 根据实际问题构造一个概率统计模型,把“原始问题的解”转化为模型中随机变量的分布特征或事件发生概率。这一步是整个模拟实验的核心,要求我们对问题的数学本质进行抽象与刻画,将现实中的不确定性因素用概率分布来描述,使问题可以通过随机数生成和统计分析的方法进行求解。
- 设计合理的模拟方案,确定模拟次数、抽样方法及统计量计算方式,保证模拟结果的稳定性与可靠性。
- 利用随机数生成技术产生模拟数据,按照设定的概率分布或条件,生成大量符合模型设定的随机样本。
- 对模拟数据进行统计分析,计算所需的统计量或事件概率,进而估计原问题的解。
- 评价与检验模拟结果,通过比较理论值、已知情况或误差分析,检验模拟方案的有效性和模拟结果的可信度。
整个过程强调“以随机代替必然、以大量实验逼近真值”,是解决复杂或解析解困难问题的重要数值方法。



 浙公网安备 33010602011771号
浙公网安备 33010602011771号