统计计算——随机数产生的理论与实现

在数据科学、模拟仿真、游戏开发、密码学和机器学习等领域，随机数的应用几乎无处不在。我们用它们来生成模拟样本、拆分训练测试集、控制程序随机化过程，甚至用来生成加密密钥。虽然名字叫“随机数”，但计算机本质上是确定性的设备，因此我们通常使用伪随机数（Pseudo-Random Numbers）来模拟真实世界中的随机性。这里系统梳理随机数的产生理论，给出三种常用方法的推导与实现，并通过案例演示它们在各类应用场景中的使用方法。

一、随机数的基本理论

在数学意义上，随机性指的是无法被完全预测的现象，表现为某一值或结果的不可预知性和不确定性。而在实际应用中，由于真实随机现象难以大规模、快速、高效地产生，人们更多地依赖计算机通过算法生成“伪随机数”，模拟真实的随机性。

1.1 真随机数与伪随机数

📌 真随机数（True Random Numbers）

真随机数是基于自然界中的随机现象产生的随机数。常见的来源包括：

  • 大气噪声
  • 放射性衰变
  • 硬件电路噪声
  • 光子事件

这类随机数的最大特点是不可预测性，因为它依赖于物理过程，完全脱离计算机算法。其优点在于真正随机，缺点是产生速度慢、依赖外部设备、成本较高，且在普通计算环境下不易实现。

📌 伪随机数（Pseudo-Random Numbers）

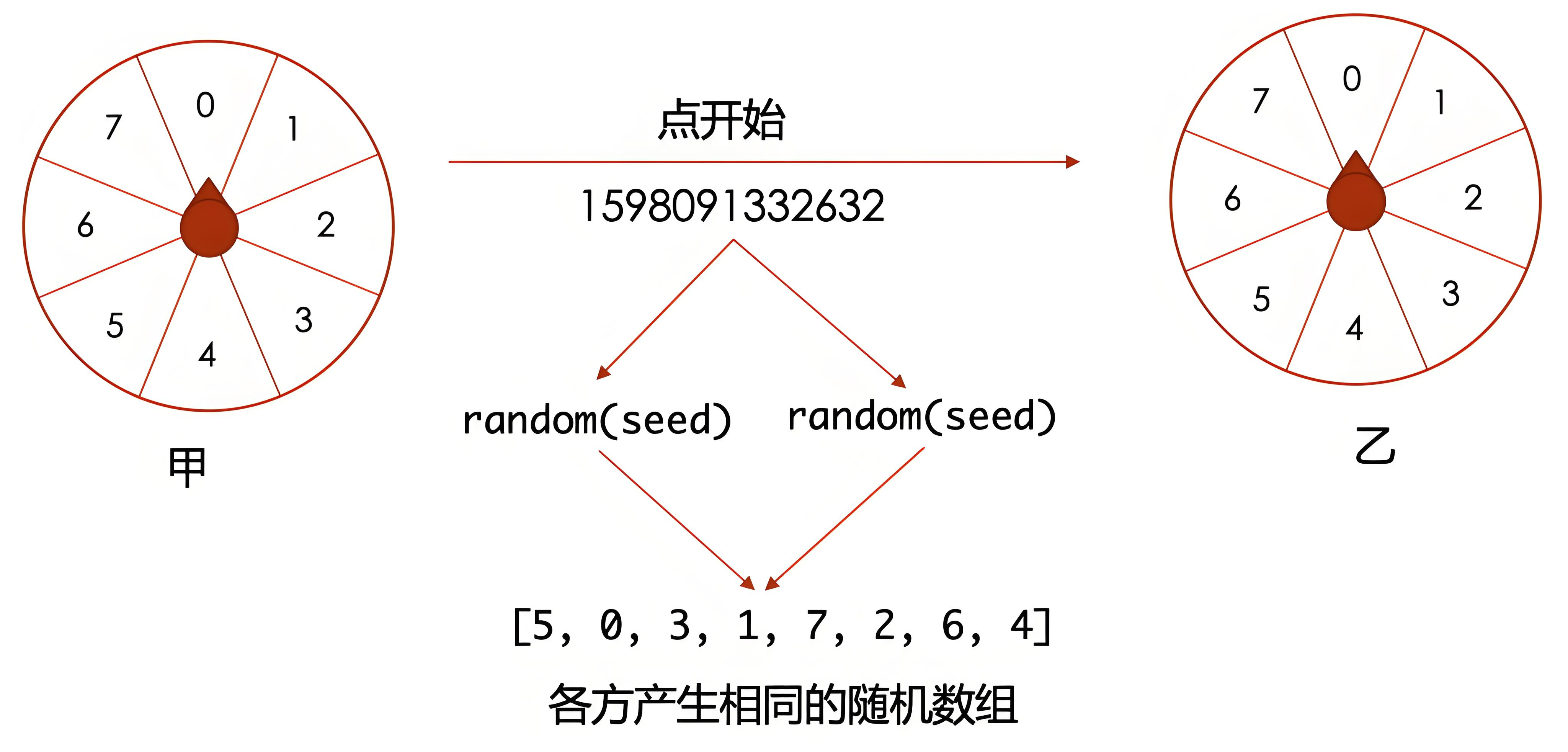
伪随机数则是通过确定性的算法计算得到的随机数。虽然看上去随机，但实际是完全由初始条件（种子 seed）和生成公式决定的。相同种子、相同算法，每次生成的伪随机序列都是一样的，因此是可复现的。
伪随机数通常用于计算机模拟和数值计算，因为它生成速度快、易于实现，且能控制结果复现性。尽管伪随机数本质上是“伪”的，但只要设计合理，它在统计性质上能很好地近似真随机数。

1.2 伪随机数的性质

一个好的伪随机数生成器（Pseudo-Random Number Generator，PRNG）应满足以下性质：

  • 周期性（Periodicity）

    • PRNG 生成的数列是有周期的，意味着在某个长度后，数列会重复。
    • 周期越长，数列“看起来”越随机，应用效果越好。

  • 均匀性（Uniformity）

    • 随机数应在指定区间（通常为 $$0,1$$）内均匀分布，满足：

      \[\lim_{N \to \infty} \frac{n(a,b)}{N} = b - a \]

      其中，$ n(a,b) $ 表示区间 \([a,b]\) 内随机数个数，$ N $ 为总数。

  • 独立性（Independence）

    • 序列内任意两个数应相互独立，前一个值不能预测下一个值。

  • 可重复性（Repeatability）

    • 相同种子和相同算法应得到相同的伪随机序列，便于程序调试、复现实验。

1.3 随机数应用场景

随机数广泛应用于科学研究、工程计算、人工智能、金融建模以及加密安全等多个领域。根据应用需求不同，随机数既可以作为数值模拟的重要基础，也能作为算法随机性保证的重要手段。

在蒙特卡洛方法中，随机数被用来模拟概率事件、估计复杂积分、计算期望值以及优化函数值。例如，利用均匀分布随机数在单位正方形内采样，统计落在单位圆内部点的比例，即可估算圆周率π。这类方法常用于高维积分、多目标优化和随机微分方程求解。
在机器学习和深度学习领域，随机数用于初始化神经网络权重、打乱数据顺序、随机采样子集（如mini-batch SGD），以及数据增强等操作。合理的随机性有助于模型避免陷入局部最优，提高模型的泛化能力。
在金融数学中，随机数被用于资产定价、风险评估和衍生品定价，如Black-Scholes模型和蒙特卡洛仿真法，通过生成随机路径，预测股票价格或期权价值的未来走势。
在密码学与安全通信中，安全级别要求极高的随机数是生成密钥、会话令牌和加密算法输入的重要来源。常用如secrets、硬件随机数发生器（TRNG）等高强度安全随机源。
随机数还广泛应用于游戏开发（如敌人行为随机化、奖励掉落）、图形学渲染（如路径追踪算法中的随机采样）、试验设计与抽样调查（如随机抽样、分组）等实际工作中。合理、规范、可控的随机数生成技术，是现代数据科学与工程技术不可或缺的重要工具。

二、常用随机数产生过程

随机数广泛应用于数值模拟、蒙特卡洛方法、密码学、机器学习等领域。常见的随机数生成方法可以分为均匀随机数生成和特定分布随机数变换两大类。

2.1 线性同余法（Linear Congruential Method, LCG）

线性同余法（Linear Congruential Method, LCG）

📌 原理与公式

线性同余法是一种经典的伪随机数生成方法，其递推公式如下：

\[X_{n+1} = (aX_n + c) \mod m \]

其中：

  • $ a $：乘数
  • $ c $：增量
  • $ m $：模
  • $ X_0 $：种子（初始值）

📌 参数选择条件

根据Hull-Dobell定理，为了保证生成序列的最大周期（即 $ m $），参数需满足以下条件：

  • $ c $ 与 $ m $ 互质
  • $ a - 1 $ 能被所有 $ m $ 的素因子整除
  • 若 $ m $ 为4的倍数，$ a - 1 $ 也必须是4的倍数

📌 Python 实现

m, a, c = 2**31-1, 1103515245, 12345

def lcg(seed, n):
    nums = []
    x = seed
    for _ in range(n):
        x = (a * x + c) % m
        nums.append(x / m)
    return nums

random_nums = lcg(123, 10)
print(random_nums)

📌 应用案例

  • C语言 rand() 实现方式
  • Python random.seed() 内部机制之一

2.2 中位数平方法（Middle Square Method）

📌 原理与公式

由冯·诺依曼（Von Neumann）提出，操作步骤：

  • 取种子 \(X_0\)
  • 计算 \(X_0^2\)
  • 从平方结果中取中间若干位作为新值$ X_1 $
  • 重复以上步骤

公式形式化：

\[X_{n+1} = \text{middle_digits}(X_n^2) \]

📌 Python 实现

def middle_square(seed, n, digit=4):
    nums = []
    x = seed
    for _ in range(n):
        square = str(x**2).zfill(2*digit)
        mid = square[digit//2:digit+digit//2]
        x = int(mid)
        nums.append(x / (10**digit))
    return nums

random_nums = middle_square(5735, 10)
print(random_nums)

📌 应用案例

  • 冯·诺依曼最早提出
  • 适合教学演示，易退化，周期短

2.3 梅森旋转算法（Mersenne Twister）

📌 原理

  • 使用位移、掩码和线性递推
  • 基于梅森素数 \(2^{19937}-1\)
  • 周期超长 $2^{19937}-1 $

📌 Python 实现

Python自带 random 模块：

import random

random.seed(123)
random_nums = [random.random() for _ in range(10)]
print(random_nums)

📌 应用案例

  • Python random
  • Numpy numpy.random
  • MATLAB rand
  • C++ std::mt19937

2.4 逆变换法（Inverse Transform Method）

📌 原理

利用目标分布的累计分布函数 (CDF) 的反函数将 \([0,1]\) 均匀分布随机数映射到目标分布。

公式：$$X = F^{-1}(U)$$
其中

  • $ U $ 为 \([0,1]\) 区间均匀分布随机数
  • $ F $ 为目标分布的 CDF

📌 指数分布案例

若目标分布为参数为\(\lambda\) 的指数分布：

\[F(x) = 1 - e^{-\lambda x} \]

求其反函数：

\[x = -\frac{1}{\lambda} \ln(1-U) \]

📌 Python实现

import math
import random

def exp_random(lmbda, n):
    return [-math.log(1-random.random())/lmbda for _ in range(n)]

print(exp_random(1.5, 10))

2.5 Box-Muller法（正态分布生成）

📌 原理

将两个\([0,1]\)均匀分布随机数\(U_1, U_2\)变换为标准正态分布随机数：

\[Z_0 = \sqrt{-2 \ln U_1} \cos(2\pi U_2)\\ Z_1 = \sqrt{-2 \ln U_1} \sin(2\pi U_2) \]

📌 Python实现

def box_muller(n):
    import math, random
    nums = []
    for _ in range(n//2):
        u1, u2 = random.random(), random.random()
        z0 = math.sqrt(-2 * math.log(u1)) * math.cos(2 * math.pi * u2)
        z1 = math.sqrt(-2 * math.log(u1)) * math.sin(2 * math.pi * u2)
        nums.extend([z0, z1])
    return nums

print(box_muller(10))
方法 特点 周期长度 适用场景
线性同余法 (LCG) 简单高效，周期有限 \(\leq m\) C语言、Python种子机制
中位数平方法 原理简单，易退化 通常很短 教学用途
梅森旋转算法 超长周期，均匀性极好 \(2^{19937}-1\) Python/Numpy/C++内置算法
逆变换法 通用性强，需CDF反函数 取决于均匀随机数源 指数、泊松、几何分布等
Box-Muller法 简单易用，适合正态分布 均匀源周期的1/2 正态分布样本生成，蒙特卡洛模拟

三、现代随机数库简介

在现代编程与科学计算中，随机数的应用无处不在，从模拟、优化到加密，都需要依赖高质量的随机数生成器。各类语言和库提供了丰富的接口，以下进行系统整理：

3.1 Python 随机数库

  • random 模块
    Python 标准库自带，基于 Mersenne Twister 算法（周期超长 219937−12^{19937}-1219937−1），提供如 random(), randint(), uniform() 等常用函数，适合普通仿真、教学用途。

  • numpy.random
    数值计算专用库 Numpy 内置的随机模块，提供更高效的向量化随机数生成，支持多种分布（正态、泊松、二项等），适合大规模科学计算。

  • randomgen
    更先进的随机数库，内置多种现代生成器（如 PCG64、Xoshiro256**），性能优异，分布种类丰富，适用于需要控制种子和可重复性的大型模拟。

  • 加密安全随机数

    • secrets：Python 3.6+ 内置模块，基于操作系统底层熵源，适合密码学、密钥、验证码生成。
    • os.urandom：返回操作系统提供的随机字节流，安全性强，常用于 token、会话ID生成。

3.2 R语言随机数库

  • runif()：生成均匀分布随机数。
  • rnorm()：生成正态分布随机数。

R语言内置的随机数生成函数，均支持设置种子 set.seed()，便于复现实验结果，广泛应用于统计模拟与蒙特卡洛方法。

3.3 MATLAB 随机数库

  • rand()：生成[0,1]区间均匀分布随机数。
  • randn()：生成标准正态分布随机数。

MATLAB 内置基于 Mersenne Twister 和其他算法的随机数库，适合工程、数值计算场景，支持状态控制与种子设定。

3.4 C++ 随机数库

  • std::mt19937 (C++11)
    C++11 引入 <random> 标准库，std::mt19937 实现 Mersenne Twister 算法，结合 std::uniform_real_distribution、std::normal_distribution 可生成多种分布，适合高性能仿真与系统开发。

对比小结

语言/库 主要特点 适用场景
random 简单易用，Mersenne Twister 基础随机需求、教学
numpy.random 向量化运算，高效 科学计算、大规模模拟
randomgen 多算法选择，现代高效 高性能随机、蒙特卡洛
secrets 加密安全，基于系统熵源 密码学、验证码生成
os.urandom 底层随机字节流 token、安全密钥
R runif() 均匀分布随机数，带种子设定 统计模拟、仿真
R rnorm() 正态分布随机数 蒙特卡洛、统计建模
MATLAB rand() 均匀分布 工程仿真、数值计算
MATLAB randn() 标准正态分布 统计仿真、建模分析
C++ std::mt19937 高性能 Mersenne Twister 系统开发、模拟器

四、 随机数的应用

4.1 几何随机变量的生成

几何随机变量（Geometric Random Variable）表示在伯努利试验中，直到第一次成功所需的独立试验次数。其概率质量函数（PMF）为：

\[P(X = k) = (1-p)^{k-1} p \]

其中：

  • $ p $：单次试验成功概率
  • $ k $：第 $ k $ 次试验首次成功（$ k=1,2,3,\dots $）

📌 随机数生成原理

根据逆变换法，先对几何分布的累积分布函数（CDF）求逆。

几何分布的 CDF：

\[F(k) = 1 - (1-p)^k \]

令 $ U \sim U(0,1) $，则有：

\[F(k) \geq U \]

代入公式：

\[1 - (1-p)^k \geq U \]

化简：

\[(1-p)^k \leq 1-U \]

两边取对数：

\[k \geq \frac{\ln(1-U)}{\ln(1-p)} \]

由于 $ k $ 是正整数，取上取整：

\[k = \left\lceil \frac{\ln(1-U)}{\ln(1-p)} \right\rceil \]

其中 $ \lceil \cdot \rceil $ 表示向上取整。

📌 Python 实现

import math
import random

def geometric_random(p, n):
    nums = []
    for _ in range(n):
        u = random.random()  # 生成 U ~ U(0,1)
        k = math.ceil(math.log(1-u) / math.log(1-p))  # 逆变换公式
        nums.append(k)
    return nums

# 生成 10 个 p=0.3 的几何随机数
random_numbers = geometric_random(0.3, 10)
print(random_numbers)

4.2 数学期望估计

假设从连续型随机变量 $ X \sim f_X(x) $ 中抽样 $ n $ 个样本 $ x_1, x_2, \dots, x_n $，有：

\[\mathbb{E}_X[g(X)] = \int_X f_X(x) g(x) dx \approx \frac{1}{n} \sum_{i=1}^n g(x_i) \]

当 $ n \to \infty $ 时，这个平均值趋近于理论期望。

📌 估计 $ \pi $

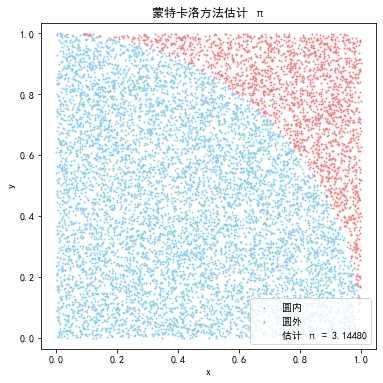
我们可以用蒙特卡洛方法，通过均匀分布随机采样，估计单位圆内的面积（即 $ \pi $）。

  • 在正方形 \([0,1] \times [0,1]\) 内随机投点
  • 点在单位圆内的概率是 $ \frac{\pi}{4} $
  • 用落入圆内点的比例估计 $ \pi $

\[\pi \approx 4 \times \frac{\text{圆内点数}}{\text{总点数}} \]

📌 Python 验证

import numpy as np
import matplotlib.pyplot as plt
import matplotlib

# 设置中文和负号正常显示
matplotlib.rcParams['font.sans-serif'] = ['SimHei']
matplotlib.rcParams['axes.unicode_minus'] = False

# 设置采样点数量
N = 10000
# 生成 [0,1] 均匀分布随机点
x = np.random.uniform(0, 1, N)
y = np.random.uniform(0, 1, N)

# 计算是否在单位圆内
inside_circle = x**2 + y**2 <= 1

# 估计 pi
pi_estimate = 4 * np.sum(inside_circle) / N
print(f"估计的 π 值: {pi_estimate}")

# 作图
plt.figure(figsize=(6,6))
# 圆内点
plt.scatter(x[inside_circle], y[inside_circle], color='skyblue', s=1, label='圆内')
# 圆外点
plt.scatter(x[~inside_circle], y[~inside_circle], color='lightcoral', s=1, label='圆外')
# 辅助线
plt.plot([], [], ' ', label=f'估计 π = {pi_estimate:.5f}')
plt.legend()
plt.title('蒙特卡洛方法估计 π')
plt.xlabel('x')
plt.ylabel('y')
plt.axis('equal')
plt.show()

总结

系统性介绍了随机数生成的基本理论、公式推导、常用方法及其 Python 实现，重点讲解了线性同余法（LCG）、中位数平方法（Middle Square Method）以及应用最广泛的梅森旋转算法（Mersenne Twister）三种经典伪随机数生成方式。针对连续型随机变量，还分别介绍了逆变换法与Box-Muller变换法，并配合 Python 实例详细实现，便于读者理解与应用。
在实际应用中，随机数生成方法的选择至关重要。小型嵌入式设备或简单程序对性能和资源消耗敏感，通常采用LCG这类结构简单、易实现的生成器。对于要求高精度和大规模仿真的科学计算、机器学习任务，优先推荐周期超长、分布均匀性优良的梅森旋转算法。而在密码学、身份验证、加密传输等安全性要求极高的场景，应使用**secrets库或基于硬件熵源的硬件随机数发生器**。
熟练掌握这些经典方法，不仅能够提升仿真、算法设计与数据分析的灵活性，还为未来在蒙特卡洛模拟、机器学习、密码安全等复杂应用场景中，提供了坚实可靠的技术支撑。

参考资料

  1. 统计计算学习
  2. 随机采样方法整理与讲解

posted @ 2025-04-18 20:09  郝hai  阅读(627)  评论(0)    收藏  举报