统计学(二十一)——统计过程控制(SPC)质量控制图
在现代制造业、医疗、服务业等众多行业中,产品和服务质量已成为企业竞争力的重要体现。随着生产过程复杂性和自动化水平的不断提高,依靠传统的终检手段已无法有效保障产品一致性与过程稳定性。统计过程控制(Statistical Process Control, SPC)应运而生,成为现代质量管理的重要方法。SPC以统计学原理为基础,通过对生产过程数据的持续监控与分析,及时发现和控制异常波动,实现“预防为主、控制过程”的质量管理目标。在SPC体系中,质量控制图(Control Chart)作为核心工具,能够实时反映过程变异情况,区分随机波动与异常波动,从而指导现场管理人员采取针对性措施,防止不良品产生。通过设定合理的控制界限,质量控制图不仅用于过程判异,更为企业提供过程能力分析、持续改进的重要依据。

📖 一、统计过程控制(SPC)概述
随着工业化进程的加快以及生产规模的不断扩大,产品制造过程愈发复杂,传统依赖终检的方法已无法有效保障产品质量和过程稳定。早期的质量管理主要依靠操作工人的经验或最终产品检验来发现问题,这种“事后把关”方式往往导致返工、报废等问题频发,既浪费资源,又难以满足现代生产对高效率、高一致性和高可靠性的要求。在这一背景下,统计过程控制(Statistical Process Control, SPC)应运而生,成为现代质量管理体系中不可或缺的重要组成部分。
统计过程控制(SPC)是以数理统计理论为基础,通过收集、整理和分析生产过程中的关键质量数据,利用控制图等工具对过程状态进行实时监控的方法。SPC 的核心理念是“控制过程、保证结果”,通过对过程数据的动态监控,及时发现异常波动和趋势,迅速采取措施,从而在源头上预防缺陷的发生,实现“以防为主、控制为辅”的质量管理目标。
SPC 的最大特点在于它能够区分过程中的随机波动与异常波动。在任何生产过程中,由于机器误差、材料差异、环境变化以及人员操作等因素的影响,产品质量特性值都会出现一定范围内的自然波动,这是不可避免的,被称为“随机波动”或“自然波动”。然而,如果因设备故障、操作失误、材料异常等原因导致过程偏离正常状态,就会产生“异常波动”或“特殊原因波动”,这类波动若不及时发现和控制,极易导致产品不合格甚至生产事故。SPC 通过设定合理的控制界限,利用控制图实时追踪过程数据的波动情况,帮助管理者区分两类波动,确保过程运行在受控状态。
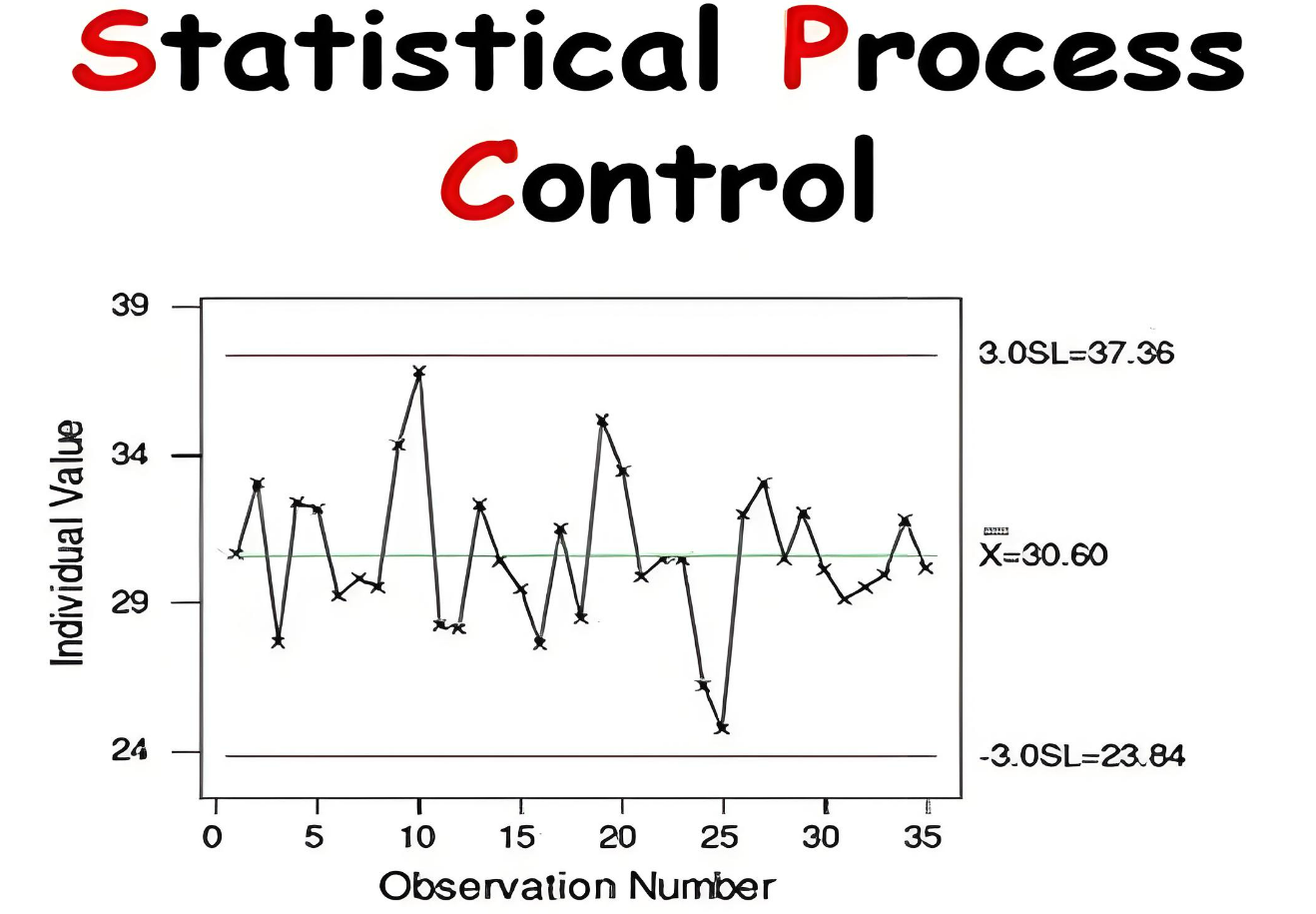
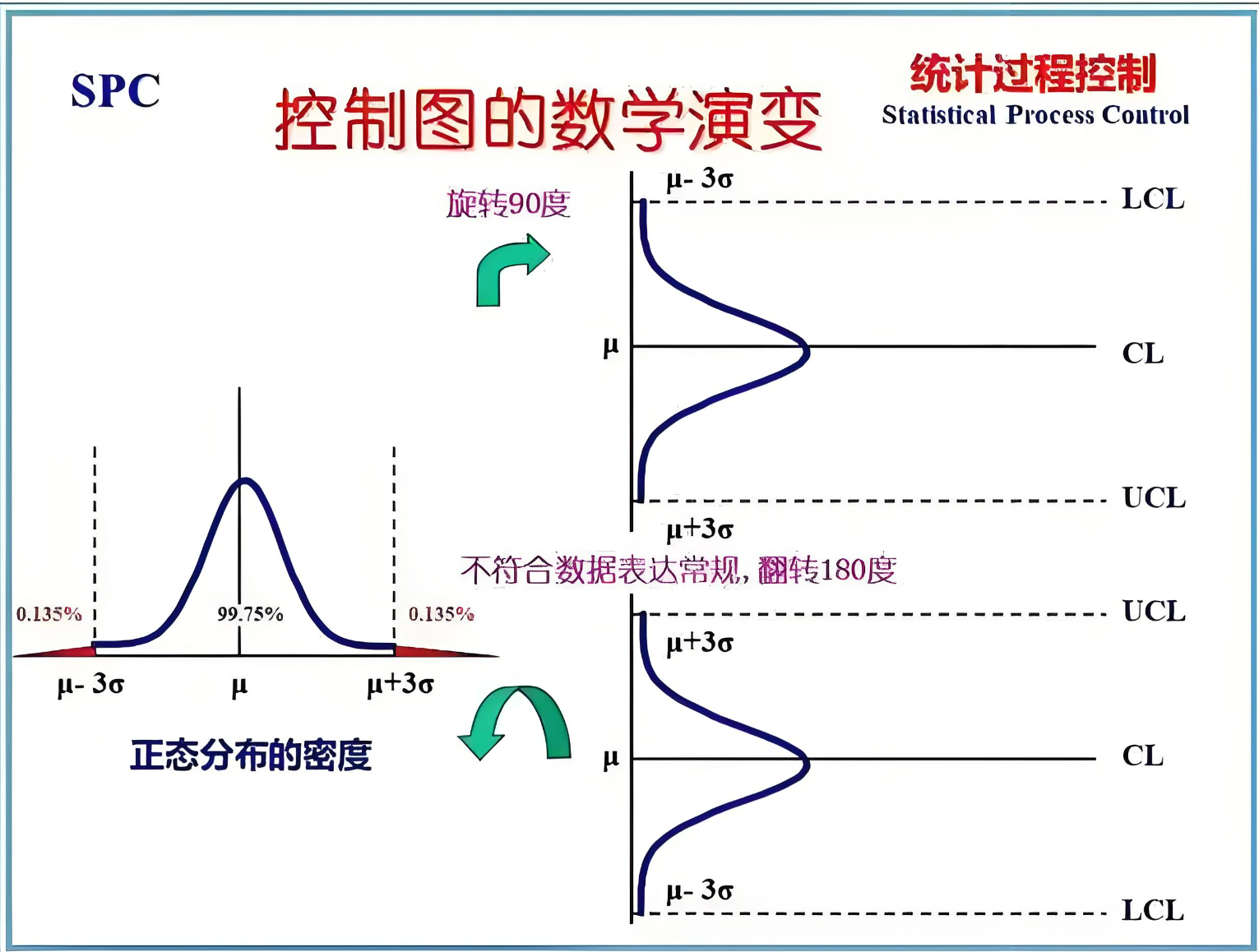
控制图是 SPC 中最核心、应用最广泛的工具。它以时间顺序记录过程数据,并根据统计方法计算出中心线(CL)、上控制界限(UCL)和下控制界限(LCL)。当过程数据点均落在控制界限内且无异常模式时,表明过程处于受控状态,仅存在随机波动;当数据点超出控制界限或出现趋势、循环等特定模式时,说明过程受到异常因素影响,需要及时查明原因并采取纠正措施。控制图不仅能够反映当前过程稳定性,还能预测过程未来的变化趋势,是实现持续改进和过程优化的重要依据。
自20世纪20年代,美国贝尔实验室的工程师沃尔特·A·休哈特(Walter A. Shewhart)首次提出控制图理论以来,SPC 理论与方法不断发展,广泛应用于机械制造、电子、汽车、医疗、食品、化工等各个行业。尤其在六西格玛管理体系中,SPC 被视为过程改进的重要工具,有效支撑了DMAIC(定义-测量-分析-改进-控制)方法论的实施。
现代 SPC 不仅限于现场手工记录数据绘制控制图,借助信息化手段,SPC 系统能够实现自动数据采集、实时控制图绘制、异常自动报警、趋势分析以及过程能力评估,极大提升了数据分析效率与决策及时性。同时,SPC 也为智能制造与工业4.0 提供了强有力的数据基础和质量保障。
统计过程控制(SPC)作为现代质量管理的重要方法体系,以统计理论为依据,通过控制图等工具对生产过程进行实时监控,有效预防和控制异常波动,确保过程稳定和产品一致性,为企业提升产品质量、降低成本、增强市场竞争力发挥着至关重要的作用。
📖 二、八大质量控制图
在实际生产过程中,产品质量受到人、机、料、法、环、测等多种因素的影响,产品的属性和尺寸不可避免地会出现变差。即便在相同的工艺、相同的设备和相同操作方法下,两个零件的尺寸也几乎不可能完全相同。这种变差通常由以下两类原因引起:
- 普通原因(Common Causes):指过程内固有的、随机性波动,是由大量微小因素叠加所致,难以单独识别。它是过程自然特性的一部分,通常需要通过改进工艺或设备来降低其影响。
- 特殊原因(Special Causes):指由特定、可识别的异常因素导致的波动,例如设备故障、操作失误、原材料异常、环境剧烈变化等。这类变差是异常的、可控的,应及时发现并纠正。
📌 2.1 SPC的目的
通过统计方法监控生产过程,判断过程是否处于受控状态,及时发现由特殊原因导致的异常波动,避免批量性不良品的发生,提高产品一致性与过程稳定性。此外,SPC还是产品开发和质量策划(APQP)过程中的重要环节,特别是在产品和过程确认阶段,如试生产、首件确认、初始过程能力研究,以及正式量产阶段。通过SPC技术,可以实现以下目标:
- 监控过程稳定性与一致性
- 发现并排除异常波动
- 保障产品质量,降低质量成本
- 提升过程能力,提高客户满意度
- 为持续改进提供数据依据
因此,SPC不仅是控制,更是改善与优化过程能力的重要工具。
| 类型 | 控制对象 | 特点 | 常用图 |
|---|---|---|---|
| 计量型控制图 | 连续型数据 | 用样本均值、极差、标准差分析 | \(\bar{X}\)-R图、\(\bar{X}\)-S图 |
| 计数型控制图 | 离散型数据 | 计数型质量特性 | \(p\)图、\(np\)图、\(c\)图、\(u\)图 |
📌 2.2 控制图简要
| 序号 | 类型 | 名称 | 符号 | 特点 | 适用场景 |
|---|---|---|---|---|---|
| 1 | 计量型 | 均值-极差控制图 | \(\bar{X}\)-R | 同时监控样本均值与极差,适合小样本 (n ≤ 10) | 连续型数据,如零件尺寸、重量、温度等,样本容量小 |
| 2 | 计量型 | 均值-标准差控制图 | \(\bar{X}\)-S | 同时监控样本均值与标准差,适合大样本 (n > 10) | 连续型数据,样本容量较大(如连续生产过程的质量指标监控) |
| 3 | 计量型 | 中位数-极差控制图 | 中位数-R | 以中位数代替均值,适用于数据分布偏态或极端值多的情况 | 连续型数据,分布偏态或含离群值,如化学分析测试数据 |
| 4 | 计量型 | 单值-移动极差控制图 | X-MR | 逐个监控单个数据点及相邻数据点间的差异,适合无法分组的单件数据 | 连续型数据,单件测量,如工序间时间间隔、设备温度、单件尺寸 |
| 5 | 计数型 | 不合格品率控制图 | P | 监控单位产品中不合格品的比例,适合样本容量不固定 | 离散型数据,产品外观检验、电子元件检验 |
| 6 | 计数型 | 不合格品数控制图 | nP | 监控单位产品中不合格品数量,适合样本容量固定 | 离散型数据,如成批检测、电子产品检测 |
| 7 | 计数型 | 单位缺陷数控制图 | U | 监控每单位产品的缺陷数,样本容量不固定 | 离散型数据,如板材表面缺陷数量、电子设备故障数 |
| 8 | 计数型 | 缺陷数控制图 | C | 监控每批产品缺陷总数,样本容量固定 | 离散型数据,如每台机器上的缺陷总数、每件工件的不良点数 |
📖 三、XBar-R控制图核心要素和算法原理
XBar-R控制图(均值-极差控制图)是统计过程控制(SPC)中最常用的计量型控制图之一,专门用于监控生产过程中样本均值与极差的变动情况。它通过两个子图共同作用:
- XBar图:监控过程中心(均值)变化情况
- R图:监控过程波动(极差)情况
两者配合使用,能同时掌握过程均值的稳定性与数据波动程度,有效识别特殊原因波动,保证过程持续受控。
📌 3.1 核心要素
| 控制图 | 中心线 | 上控制限 | 下控制限 | 数据点 |
|---|---|---|---|---|
| XBar图 | 样本均值的均值 \(\bar{\bar{X}}\) | \(\bar{\bar{X}} + A_2 \bar{R}\) | \(\bar{\bar{X}} - A_2 \bar{R}\) | 每组样本均值 |
| R图 | 平均极差 \(\bar{R}\) | \(D_4 \bar{R}\) | \(D_3 \bar{R}\) | 每组极差 |
- A₂、D₃、D₄:依赖于样本容量 \(n\),由控制图常数表查得。
📌 3.2 算法原理推导
设每组样本容量为 \(n\),第 \(i\) 组样本值为 \(X_{i1}, X_{i2}, \cdots, X_{in}\),则:
- 该组均值:
- 该组极差:$$R_i = \max(X_{ij}) - \min(X_{ij})$$
✅ 计算中心线
- XBar图中心线(CL):$$CL_{\bar{X}} = \bar{\bar{X}} = \frac{1}{k} \sum_{i=1}^k \bar{X}_i$$
- R图中心线(CL):$$CL_R = \bar{R} = \frac{1}{k} \sum_{i=1}^k R_i$$
其中 \(k\) 为样本组数。
✅ 控制限计算
XBar图:$$UCL_{\bar{X}} = \bar{\bar{X}} + A_2 \cdot \bar{R}$$
R图:$$UCL_R = D_4 \cdot \bar{R}$$
✅ 控制图常数表(节选)
| \(n\) | \(A_2\) | \(D_3\) | \(D_4\) |
|---|---|---|---|
| 2 | 1.880 | 0 | 3.267 |
| 3 | 1.023 | 0 | 2.574 |
| 4 | 0.729 | 0 | 2.282 |
| 5 | 0.577 | 0 | 2.114 |
| 6 | 0.483 | 0 | 2.004 |
✅ 注:当 \(D_3=0\),说明极差下控制限无法为负。
📌 3.3 实际案例分析
某车间对一台数控车床加工轴直径进行质量监控,每次抽样5件,共抽样25组,记录如下(单位:mm):
| 组号 | 1 | 2 | 3 | 4 | 5 |
|---|---|---|---|---|---|
| 1 | 20.11 | 19.98 | 20.05 | 20.02 | 20.07 |
| 2 | 20.09 | 20.01 | 20.04 | 20.03 | 20.06 |
| 3 | 19.95 | 20.00 | 19.98 | 19.97 | 19.99 |
| ... | ... | ... | ... | ... | ... |
| 25 | 20.04 | 20.05 | 20.02 | 20.06 | 20.03 |
✅ ① 计算每组均值与极差
示例:
-
第1组均值:$$\bar{X}_1 = \frac{20.11+19.98+20.05+20.02+20.07}{5} = 20.046$$
-
第1组极差:$$R_1 = 20.11 - 19.98 = 0.13$$
依次计算25组均值与极差。
✅ ② 计算 \(\bar{\bar{X}}\) 与 \(\bar{R}\)
假设计算结果如下:
✅ ③ 查表得 \(A_2=0.577\),\(D_3=0\),\(D_4=2.114\)
✅ ④ 计算控制限
XBar图:$$UCL_{\bar{X}} = 20.01 + 0.577 \times 0.10 = 20.0677$$
R图:$$UCL_R = 2.114 \times 0.10 = 0.2114$$
✅ ⑤ 判异分析
- 若XBar图或R图超出控制限,说明过程异常;
- 若连续点出现异常走势(如6点递增),也视作异常。
📌 3.4 R语言实现
我们用R实现整个XBar-R控制图绘制。
# 安装并加载qcc包(如未安装)
# install.packages("qcc")
library(qcc)
# 📌 1️⃣ 输入数据:25组,每组5个数据(单位:mm)
data <- matrix(c(
20.11, 19.98, 20.05, 20.02, 20.07,
20.09, 20.01, 20.04, 20.03, 20.06,
19.95, 20.00, 19.98, 19.97, 19.99,
20.02, 20.06, 20.01, 20.03, 20.04,
20.03, 20.00, 19.99, 20.01, 20.05,
20.07, 20.02, 20.05, 20.06, 20.08,
20.05, 20.01, 20.03, 20.02, 20.04,
19.97, 19.99, 20.00, 20.02, 20.01,
20.09, 20.05, 20.06, 20.04, 20.07,
19.96, 19.95, 20.00, 20.02, 19.98,
20.08, 20.03, 20.06, 20.05, 20.07,
20.04, 20.01, 20.03, 20.02, 20.05,
19.99, 20.00, 20.01, 20.02, 19.98,
20.07, 20.04, 20.03, 20.06, 20.05,
20.03, 20.02, 20.00, 20.04, 20.05,
20.00, 19.98, 20.01, 20.02, 20.03,
20.06, 20.08, 20.04, 20.05, 20.07,
19.99, 20.01, 20.00, 20.02, 19.97,
20.05, 20.04, 20.02, 20.03, 20.01,
20.00, 20.01, 20.03, 20.02, 20.04,
20.03, 20.05, 20.02, 20.04, 20.06,
20.04, 20.02, 20.03, 20.05, 20.01,
19.98, 19.97, 20.00, 19.99, 20.01,
20.06, 20.07, 20.05, 20.04, 20.08,
20.04, 20.05, 20.02, 20.06, 20.03
), ncol = 5, byrow = TRUE)
# 📌 2️⃣ 查看数据维度
dim(data) # 应为 25 行 5 列
# 📌 3️⃣ 计算样本均值和极差
xbar <- apply(data, 1, mean)
R <- apply(data, 1, function(x) max(x) - min(x))
# 输出前5组均值和极差,检查正确性
head(cbind(xbar, R), 5)
# 📌 4️⃣ 计算XBar-R控制图参数
# 样本组数
k <- nrow(data)
# 样本容量
n <- ncol(data)
# 样本均值的均值 和 平均极差
Xbarbar <- mean(xbar)
Rbar <- mean(R)
# 查表常数
A2 <- 0.577
D3 <- 0
D4 <- 2.114
# XBar图控制限
UCL_Xbar <- Xbarbar + A2 * Rbar
LCL_Xbar <- Xbarbar - A2 * Rbar
# R图控制限
UCL_R <- D4 * Rbar
LCL_R <- D3 * Rbar
# 📌 5️⃣ 输出控制限
cat("XBar图控制限:\n")
cat(" UCL =", round(UCL_Xbar, 4), "\n")
cat(" CL =", round(Xbarbar, 4), "\n")
cat(" LCL =", round(LCL_Xbar, 4), "\n\n")
cat("R图控制限:\n")
cat(" UCL =", round(UCL_R, 4), "\n")
cat(" CL =", round(Rbar, 4), "\n")
cat(" LCL =", round(LCL_R, 4), "\n\n")
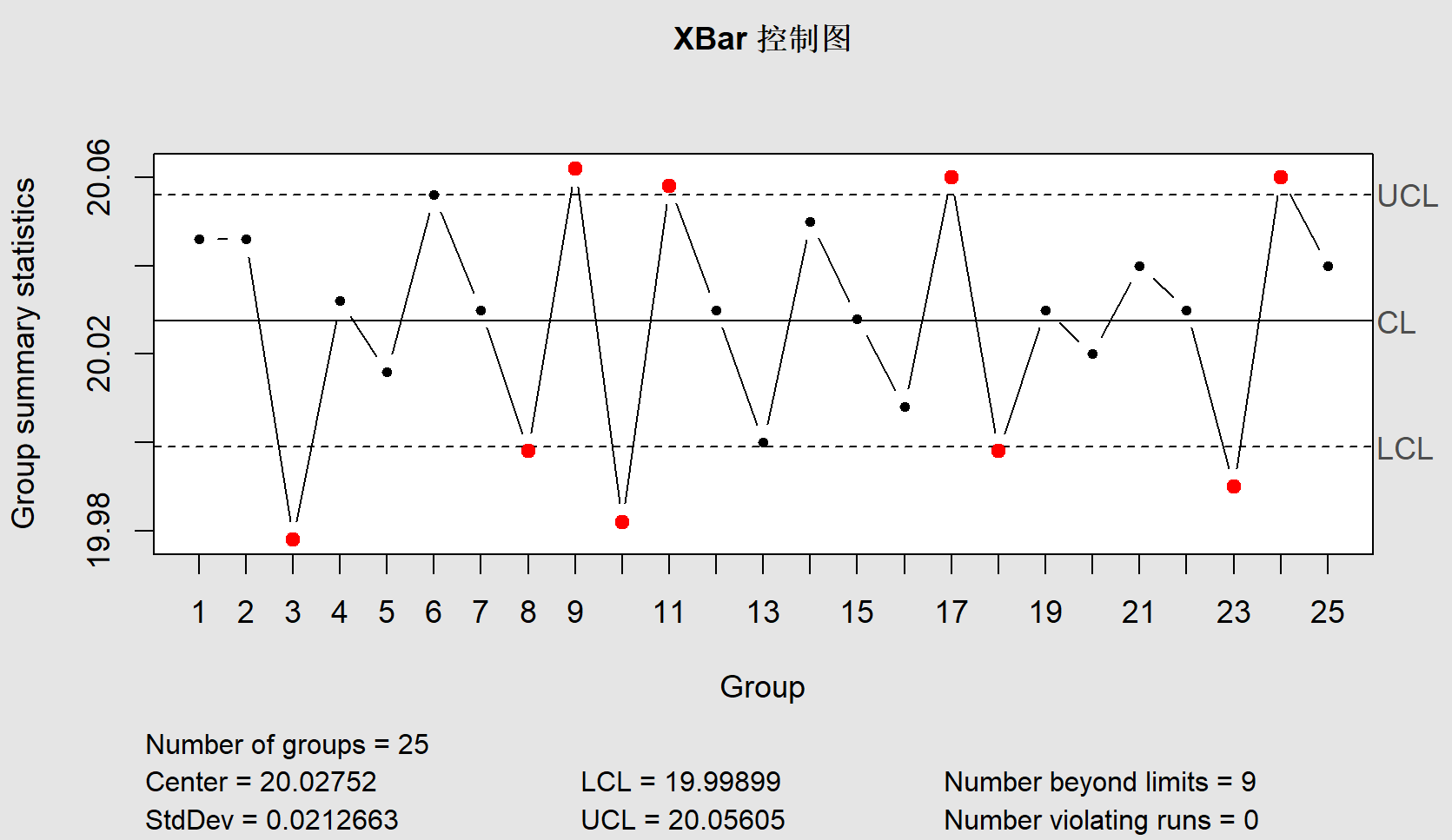
# 📌 6️⃣ 绘制 XBar-R 控制图
qcc(data, type = "xbar", nsigmas = 3, std.dev = "R", title = "XBar 控制图")
qcc(data, type = "R", nsigmas = 3, std.dev = "R", title = "R 控制图")
📖 四、6 Sigma与精益管理
在现代企业管理中,如何以科学的方法、系统的工具、持续的改进,实现产品质量提升、成本降低和顾客满意度提高,一直是企业核心竞争力建设的重要方向。其中,6 Sigma 管理方法、质量控制图(SPC)、精益管理以及持续改进理念,作为当前质量管理体系的重要组成部分,正逐步融合发展,形成协同互补的管理体系,广泛应用于制造业、医疗、服务业、信息技术等多个领域。
📌 4.1 Sigma 管理概述
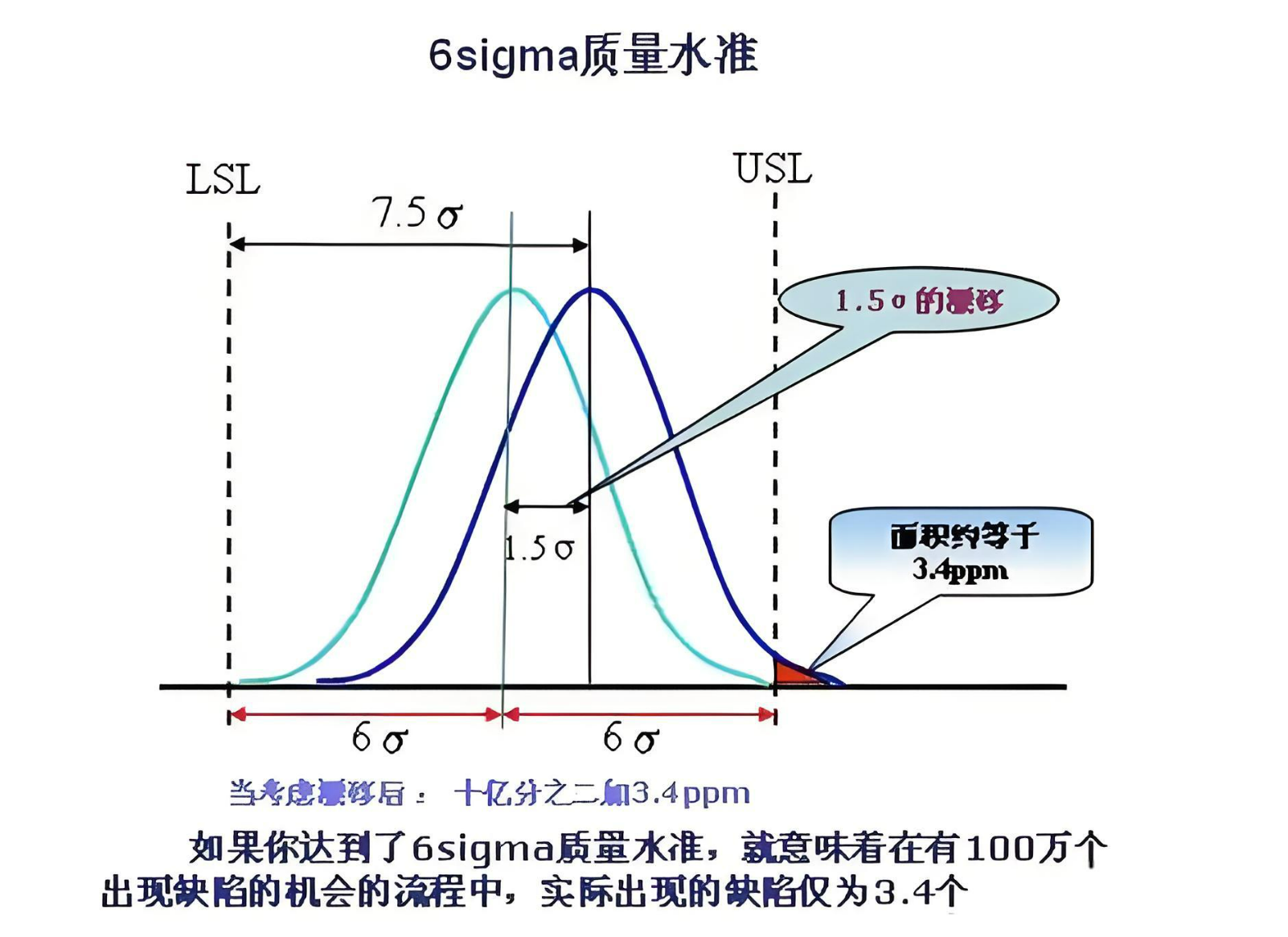
6 Sigma(六西格玛)是一种以数据和统计方法为基础,以减少缺陷、降低变异、优化过程为目标的质量管理方法。其核心思想是将过程变异控制在顾客要求范围内,使过程能力指数(Cpk)达到 2.0,即过程输出在±6σ 范围内无缺陷,约等于百万分之3.4(3.4 DPMO,Defects Per Million Opportunities)的缺陷率。
6 Sigma 管理以 DMAIC(Define、Measure、Analyze、Improve、Control)五步法为核心实施路径:
- 定义(Define):确定改进项目、明确顾客需求及关键质量特性。
- 测量(Measure):收集过程数据,评估当前绩效水平。
- 分析(Analyze):利用统计工具,分析问题根源和变异来源。
- 改进(Improve):制定并实施针对性改进措施,优化过程。
- 控制(Control):建立控制标准和监控手段,防止问题复发,维持改进成果。
在 6 Sigma 实施过程中,质量控制图作为过程监控与控制的重要工具,贯穿于数据分析、改进实施和效果监控等各个环节。
📌 4.2 质量控制图在 6 Sigma 中的应用
质量控制图是统计过程控制(SPC)体系中最重要的工具之一。它通过对过程数据的实时记录与图形化展示,配合控制界限的设定,直观地反映过程稳定性与波动性,有助于判断过程是否处于统计受控状态。
在 6 Sigma 实践中,控制图的作用主要体现在以下几个方面:
- 过程能力分析:借助控制图,评估过程输出波动范围与客户规范限(Specification Limits, SL)的匹配程度,确认过程是否具备达到 6 Sigma 水平的潜力。
- 变异识别与根因分析:通过控制图识别超出控制界限或存在非随机模式的数据点,判断异常波动发生的时间与位置,为根因分析提供依据。
- 改进措施验证:在过程优化前后,持续绘制控制图,比较数据波动情况,验证改进方案的有效性。
- 过程控制与预警:在生产现场实时监控过程数据,利用控制图自动报警,及时发现异常趋势,防止缺陷批量发生。
例如,在 DMAIC 的 Measure 阶段,企业常通过 X̄-R 控制图、P 控制图、C 控制图等多种形式,对关键质量特性进行动态监控。在 Improve 阶段,通过分析控制图趋势,调整工艺参数,优化流程设计。在 Control 阶段,通过 SPC 软件与电子化控制图系统,实现过程自动监控,提升质量管理智能化水平。
📌 4.3 精益管理与持续改进理念
精益管理(Lean Management)源于丰田生产方式,强调“消除一切浪费”,追求以最少资源创造最大价值。其核心在于持续优化流程,提升效率,降低成本,满足顾客需求。与 6 Sigma 注重“降低变异、减少缺陷”的目标不同,精益管理关注“流动性、节拍性与浪费控制”,二者目标互补,方法协同。
持续改进(Continuous Improvement)是精益管理的重要原则之一,主张企业在质量、成本、交期、效率等方面持续、小步快跑式优化。其典型方法包括 PDCA 循环(Plan-Do-Check-Act)与 Kaizen 活动。
- PDCA 循环:
- P(计划):识别问题,设定目标,制定改进计划。
- D(执行):按照计划实施改进措施。
- C(检查):评估实施效果,确认是否达成预期。
- A(处理):标准化有效措施,纳入制度,持续推广。

-
Kaizen 改善:
- 倡导全员参与,从小处着手,持续不断优化流程,消除浪费,降低成本。
企业在实施精益六西格玛(Lean Six Sigma)项目时,常通过 SPC 控制图、过程能力分析、失效模式分析(FMEA)和根因分析(Fishbone Diagram、5 Why)等多种工具,系统识别和解决质量问题,确保项目收益量化、成果可持续。
📖 五、SPC的实施建议
质量控制图作为 SPC 核心工具,通过实时监控、过程判异、溯源分析,有效保障产品质量与过程稳定性。尤其在 6σ 体系下,配合 Cp、Cpk、DPMO 等过程能力指标,为持续改进提供强有力的数据支撑。
-
推行标准化质量管理体系
企业应将质量控制图纳入日常质量管理规范,明确控制图类型、抽样方法、控制界限设定及异常处理流程,确保统计过程控制(SPC)制度化、规范化运行。 -
加强人员 SPC 培训与技能提升
操作人员、质量工程师及管理层应掌握控制图判异规则、异常分析方法与6σ改进手段,提升质量意识与数据解读能力。 -
结合信息化与自动化平台应用
借助 MES、ERP、质量管理软件,将控制图自动生成、过程监控、异常预警与改进措施闭环纳入数字化质量管理系统,实现实时在线 SPC。 -
合理选择控制图类型与判异规则
不同生产特性、样本量及变异性质,应选用恰当的控制图(如 X̄-R、p、u、EWMA、CUSUM),并根据产品特性和客户要求调整判异规则灵敏度。 -
与 Cp、Cpk、DPMO 等过程能力指标联动
控制图判异应与过程能力指数、缺陷率指标综合分析,量化过程能力,指导过程优化与资源配置决策。 -
推动6σ管理体系实施
在制造、医疗、金融、服务等行业,积极导入6σ管理方法,将 SPC 控制图与 DMAIC 改进流程结合,系统识别、控制与优化关键质量因子(CTQ),提升整体运营质量水平。
📖 总结
统计过程控制(SPC)不仅仅是一个监控生产质量的工具,它通过将统计方法与生产过程相结合,能够提前识别出潜在的质量波动并及时采取行动,从而避免了大量缺陷的产生。SPC 使用质量控制图来展示过程的稳定性,并通过实时数据分析,帮助企业对生产过程进行有效管理。它不仅能确保产品的一致性,还能在发现问题时提供科学依据,帮助管理人员制定有效的纠正措施。结合精益管理,SPC 强调消除浪费和提升效率,从而优化整体生产过程。
SPC 还为 6 Sigma 方法提供了重要的支持,它通过对数据的深入分析,帮助企业在各个环节降低变异,提高过程能力。特别是在复杂的生产环境中,SPC 能够及时捕捉到微小的变化,避免了潜在质量问题的积累,从而为企业实现持续改进提供了强有力的数据支持。6 Sigma 的核心目标是通过减少缺陷和变异来提高过程的稳定性,而 SPC 则是这一目标实现的关键工具之一。SPC 不仅有助于提高产品质量,还能降低生产成本,提升企业的市场竞争力。
参考文献



 浙公网安备 33010602011771号
浙公网安备 33010602011771号