统计学(十七)——时间序列分析概要
在现实生活和各类学科研究中,许多数据都是按照时间顺序排列的,例如每日股价、每月销售额、季度GDP、年均气温、人口数量、能源消耗等。这些数据不仅仅是孤立的数值集合,更蕴含着随时间演化的趋势、周期性、季节性波动以及随机扰动。如何通过对历史数据的科学分析,揭示数据背后的内在规律,并据此预测未来走势,是数据分析中的重要课题。时间序列分析正是研究随时间变化的数据规律性的一种统计方法。它既可以帮助我们理解变量的演变过程,识别趋势和季节性结构,又能为未来做出科学预测,指导实际决策。因此,时间序列分析在经济学、金融学、管理学、环境科学、气象学、医疗健康等众多领域得到广泛应用,成为数据分析体系中不可或缺的重要组成部分。
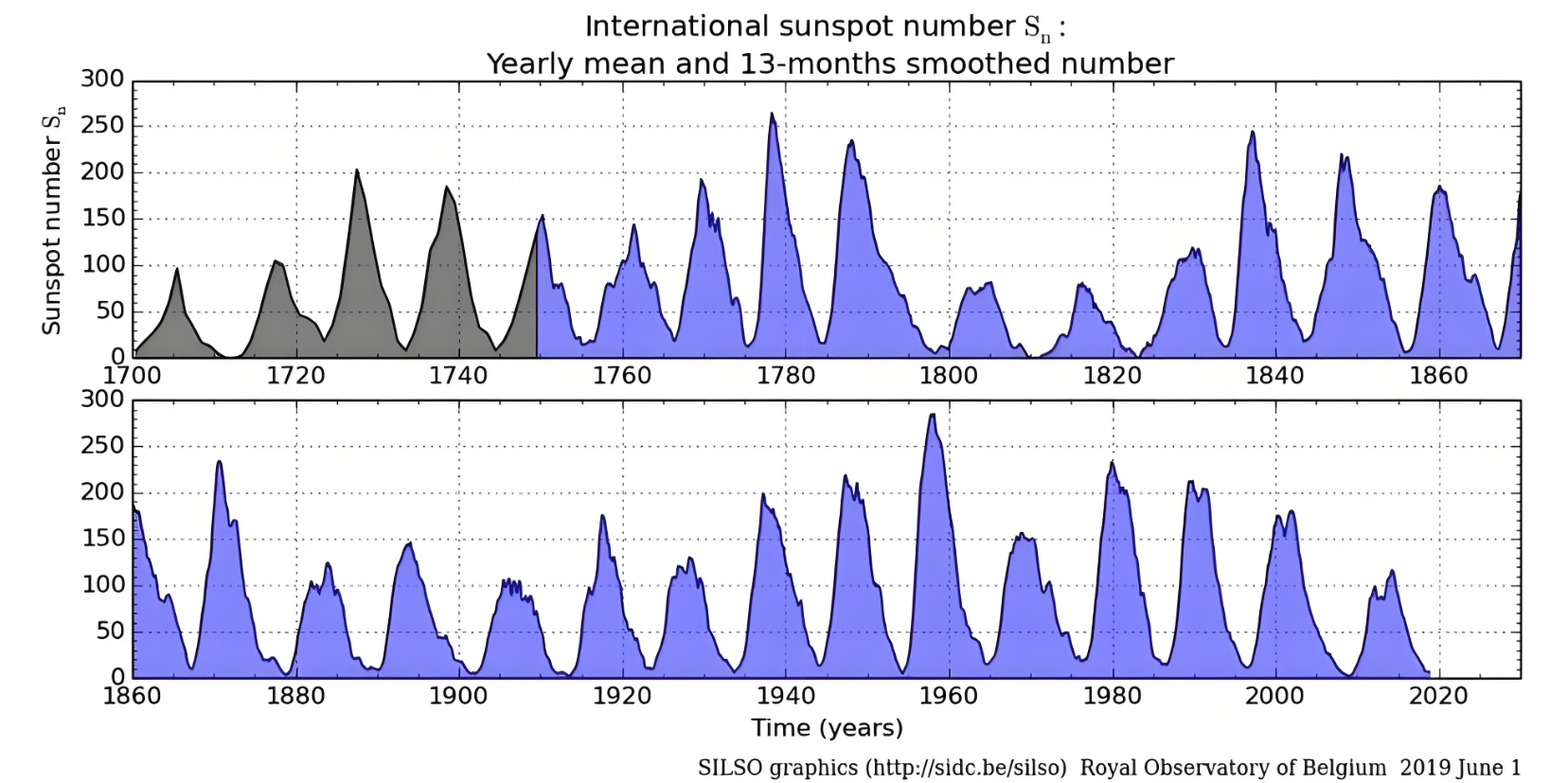
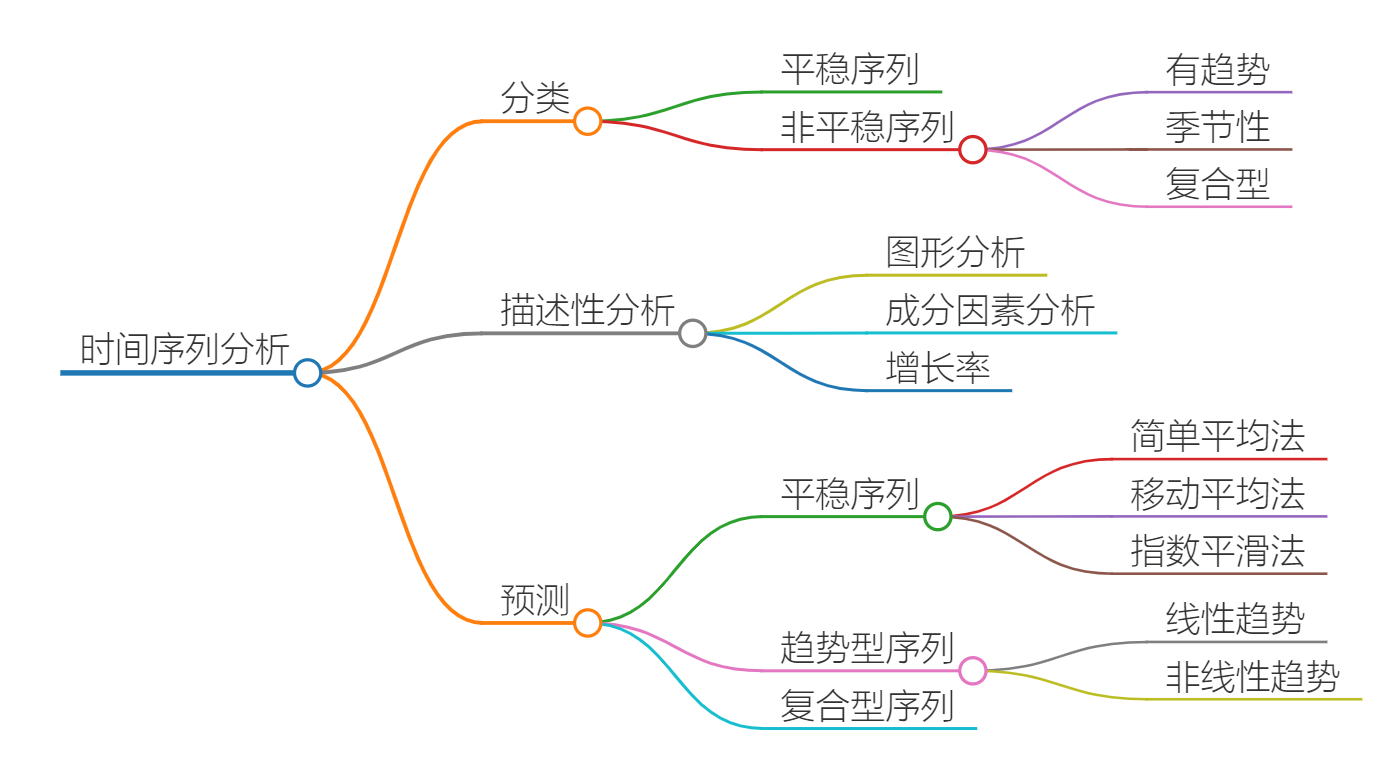
一、时间序列分类
1.1 平稳序列(Stationary Series)
在时间序列分析中,如果一个序列的统计特性在时间的推移中保持不变,我们称其为平稳序列。具体来说,平稳序列应满足以下三个条件:
- 均值保持恒定,数据的中心位置不随时间发生显著变化。
- 方差保持恒定,波动幅度稳定,数据的离散程度不随时间改变。
- 自相关系数仅取决于时间差而非时间点本身,即序列的相关性结构保持不变。
平稳序列是许多统计建模方法(如AR、MA、ARMA、ARIMA等)的基础。只有在数据稳定的前提下,我们才能合理利用已有信息预测未来。典型例子:
- 每天随机抽样的温度波动,不存在明显趋势和季节性。
- 股票市场短期价格变动,由大量微小波动组成。
- 随机波动的误差项,符合白噪声性质。
#生成平稳序列
set.seed(123)
ts_stationary <- ts(rnorm(120, mean=10, sd=1), frequency=12, start=c(2020,1))
plot(ts_stationary, main="模拟平稳序列", col="blue", lwd=2)
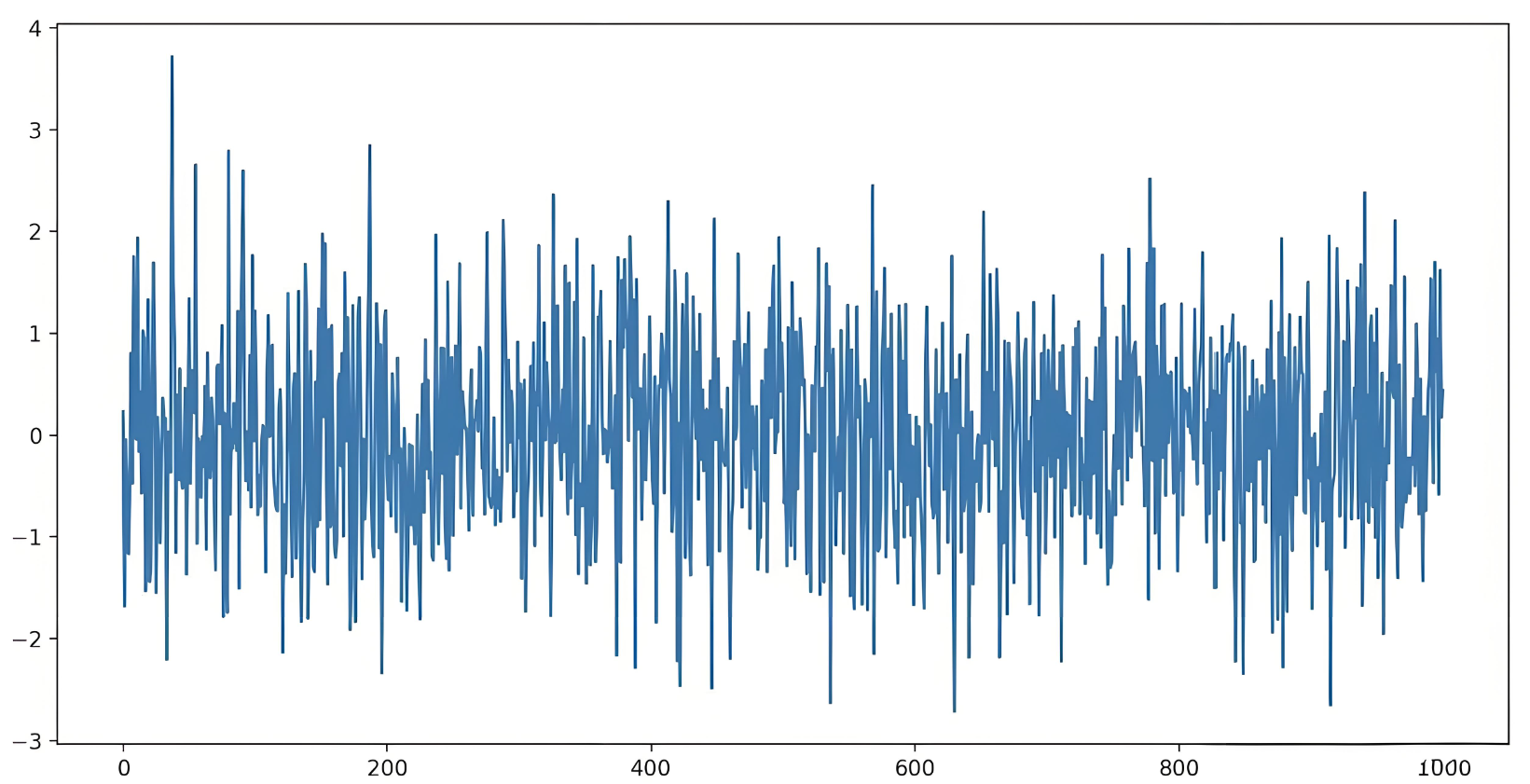
1.2 非平稳序列(Non-Stationary Series)
当序列的均值、方差或相关结构随时间发生显著变化,即表现出趋势性、季节性或其他非稳定特征时,该序列被称为非平稳序列。非平稳序列无法直接进行大多数时间序列模型拟合,需要先行差分、平稳化或选用适配的模型。
📌 a. 有趋势型
数据随时间呈现单调上升或下降的趋势。长期以来,经济、人口、气象等指标大多属于此类。
#R模拟
trend_series <- ts(1:120 + rnorm(120, 0, 5), frequency=12, start=c(2020,1))
plot(trend_series, main="有趋势型序列", col="red", lwd=2)
📌 b. 季节性型
序列存在固定周期内反复出现的规律性波动,例如一年内四季气温变化,节假日销售波动等。
#R模拟
seasonal_series <- ts(rep(c(10,20,30,40,50,40,30,20,10,20,30,40), 10) + rnorm(120, 0, 2),
frequency=12, start=c(2020,1))
plot(seasonal_series, main="季节性型序列", col="orange", lwd=2)
📌 c. 复合型
复合型时间序列同时包含趋势性和季节性成分,数据表现出随时间持续增长并叠加周期性波动的特征。
#R模拟
composite_series <- ts(1:120 + rep(c(10,20,30,40,50,40,30,20,10,20,30,40), 10) + rnorm(120,0,5),
frequency=12, start=c(2020,1))
plot(composite_series, main="复合型序列", col="purple", lwd=2)
二、描述性分析
2.1 图形分析
图形分析是时间序列分析中最直观、最基础的手段。通过对时间序列绘图,我们可以快速识别数据的趋势、周期性和异常值等特征。
📖 时间序列折线图
折线图展示数据随时间变化的轨迹,是识别趋势和周期的重要工具。
plot(AirPassengers, main="国际航空客运量折线图", col="darkgreen", lwd=2)
📖 自相关图(ACF)
自相关图描绘了序列不同滞后阶数上的自相关系数,有助于判断序列平稳性与周期性特征。
acf(AirPassengers, main="国际航空客运量 自相关图")
📖 偏自相关图(PACF)
偏自相关图揭示了剔除中间滞后项影响后,当前值与滞后值之间的纯净相关程度,有助于判定AR模型阶数。
pacf(AirPassengers, main="国际航空客运量 偏自相关图")
📖 分解图
分解图将时间序列拆分为趋势(Trend)、季节(Seasonal)和随机(Random)三个部分,便于分别分析。
decomposed <- decompose(AirPassengers)
plot(decomposed)
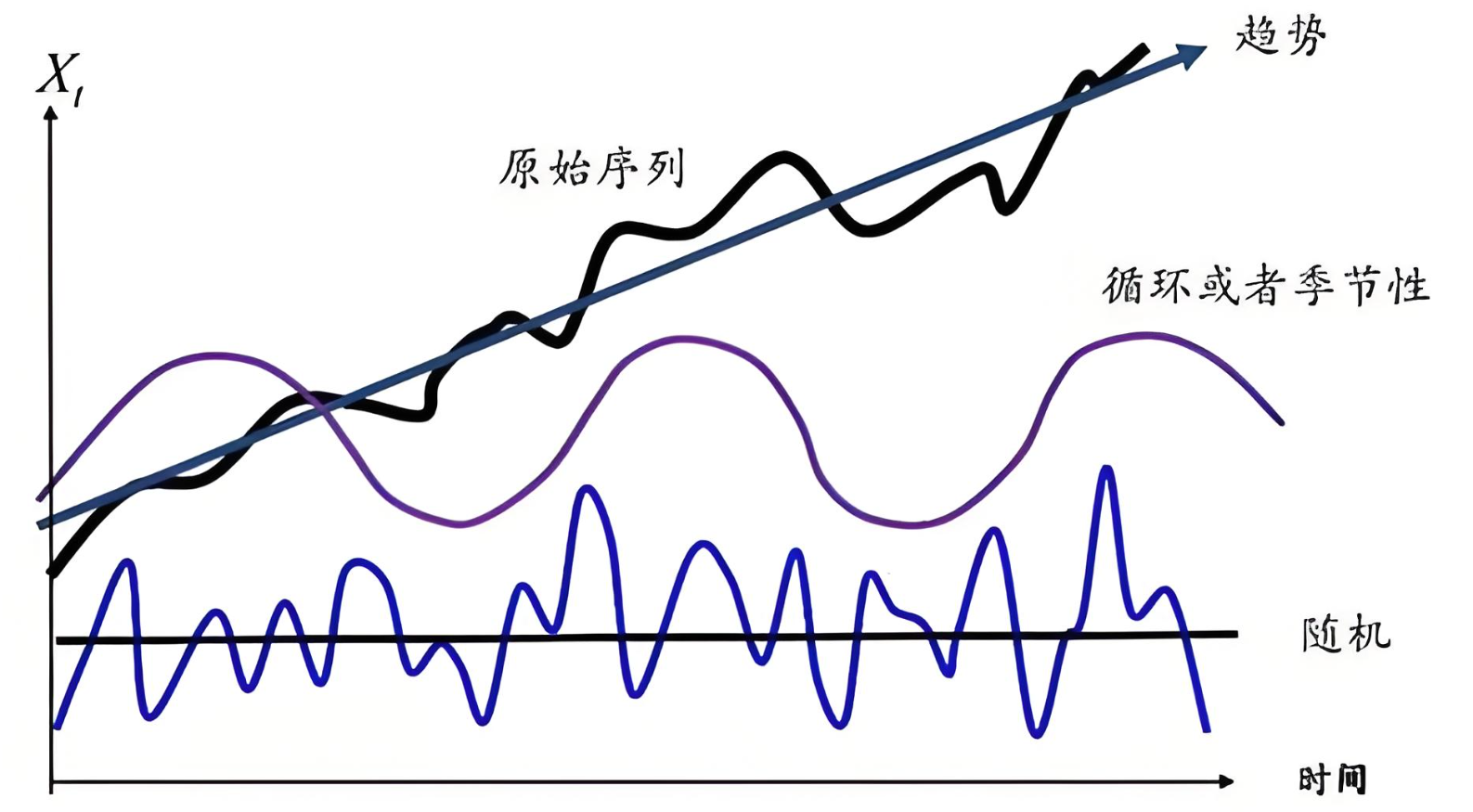
2.2 时间序列分解模型
在时间序列分析中,观测值通常由若干组成部分叠加或相乘而成,主要包括:长期趋势(Trend, T)、季节性变动(Seasonal, S)、周期性变动(Cyclical, C) 和 随机波动(Irregular, I)。根据这些成分组合方式的不同,时间序列模型主要分为加法模型和乘法模型两类,鉴于乘法模型剥离因素较为方便,一般乘法模型用的更多一些。
📖 加法模型(Additive Model)
加法模型假定时间序列的各个组成部分彼此独立且相加,适用于各成分变动幅度相对稳定的情况。数学形式表示为:
其中,$ Y_t $ 表示时间点 $ t $ 的观测值,$ T_t $ 表示趋势成分,$ S_t $ 表示季节成分,$ C_t $ 表示周期成分,$ I_t $ 表示随机扰动成分。适用场景:
- 当季节性波动幅度恒定,随时间不发生显著变化。
- 例如:日常温度、日常乘客人数、季度产量等。
📖 乘法模型(Multiplicative Model)
乘法模型则假定时间序列的组成部分之间是相互作用、相乘的关系,适用于季节性或周期性波动随趋势变化而成比例放大的情况。数学形式为:
与加法模型不同,这里各部分相乘,波动幅度随趋势水平变化而扩大或缩小。适用场景:
- 当季节性波动幅度随趋势水平变动而变化。
- 例如:随着经济总量上升,季度 GDP 增量或股市波动幅度也随之扩大。
2.3 增长率分析
增长率分析可以量化时间序列中变量变动的幅度与速度,是常见的经济指标分析方法之一。
在时间序列分析以及经济统计、财务分析等领域中,基期和报告期是两个非常重要的时间概念,常用于对不同时点或不同时期的数据进行比较和分析。
基期(Base Period)是指用作比较标准的时间点或时间段,通常选择一个具有代表性、相对稳定的时期作为基准。它的作用是作为参照系,用于衡量其他时期的变化情况。
报告期(Reporting Period)是指实际所要观察、统计、分析或预测的数据所属的时间点或时间段。报告期可以是某一个具体时间点(如2023年12月),也可以是一个时间区间(如2023年第一季度、2022-2023年度)。
在实际应用中,常通过将报告期的数据与基期的数据进行对比,计算增长率、变动幅度、累计值等指标,从而反映某项指标随时间的变化趋势与发展状况。明确基期与报告期,有助于保证数据分析的逻辑严谨性与结果的可比性,也是进行时间序列建模、趋势预测与同比、环比分析的基础。
📌 环比增长率
环比增长率反映当前期相对于上期的变化速度,适合短期波动分析。
rate_month <- diff(AirPassengers) / AirPassengers[-length(AirPassengers)] * 100
plot(rate_month, type="l", main="国际航空客运量 环比增长率", col="blue")
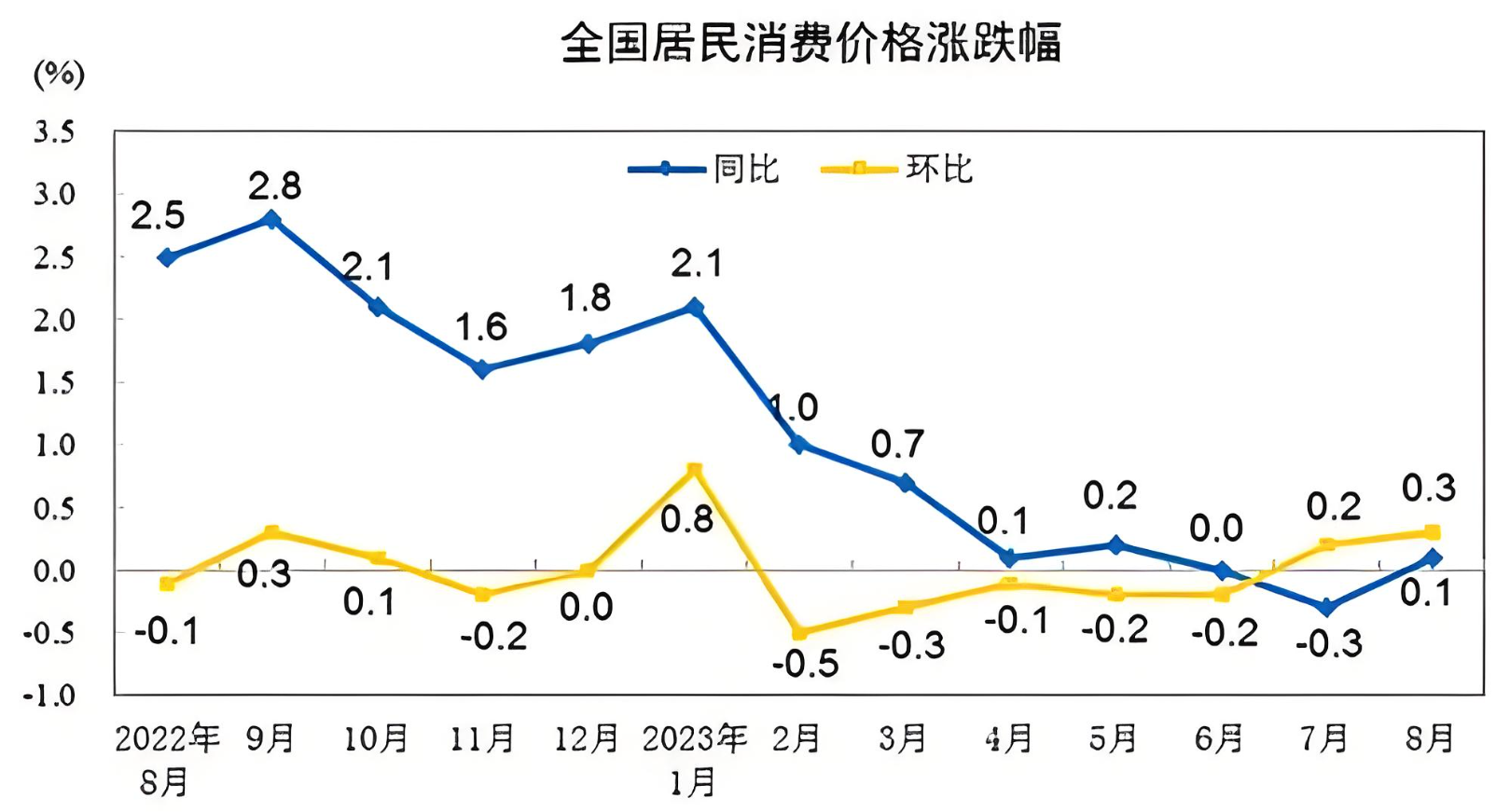
📌 同比增长率
同比增长率衡量当前期与上一年同期相比的增长情况,有助于消除季节性波动的影响。
rate_year <- diff(AirPassengers, lag=12) / AirPassengers[-(length(AirPassengers)-(0:11))] * 100
plot(rate_year, type="l", main="国际航空客运量 同比增长率", col="red")
✅ 总结表:
| 方法 | 作用 |
|---|---|
| 折线图 | 查看总体走势、季节性、周期性特征 |
| ACF图 | 判断平稳性、周期性、滞后特性 |
| PACF图 | 判定AR模型阶数,理解滞后影响结构 |
| 分解图 | 拆分趋势、季节、随机成分便于独立分析 |
| 环比/同比增长率 | 定量分析增长速率,消除季节与量纲影响 |
三、预测方法
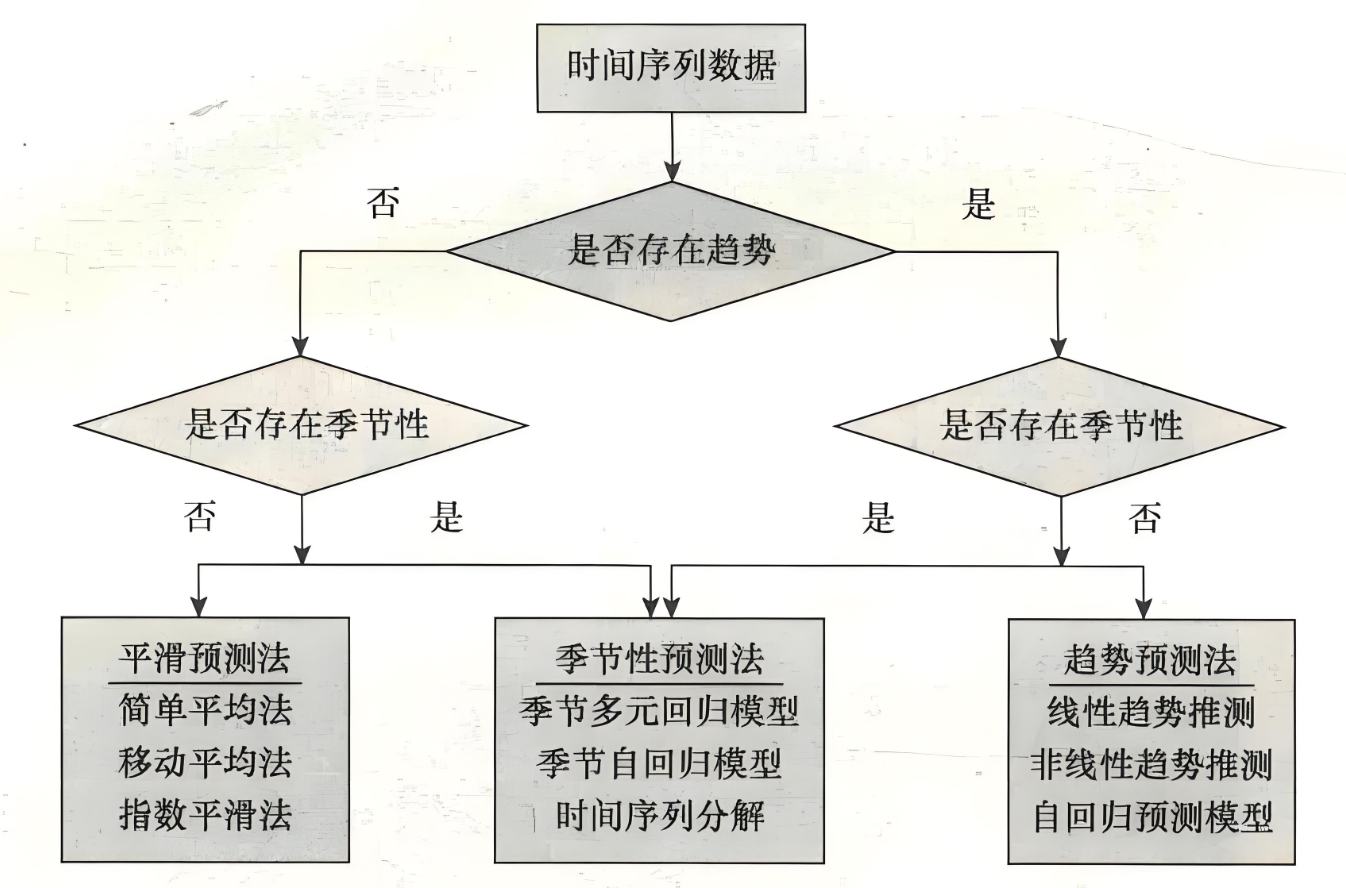
3.1 平稳序列预测
📌 简单平均法
利用历史数据的算术平均值作为未来预测值,适合于无明显趋势和季节性的平稳序列。
mean_value <- mean(AirPassengers)
abline(h=mean_value, col="red", lwd=2)
📌 移动平均法
通过计算数据在固定窗口内的平均值,平滑噪声,提取趋势成分。适合数据波动较小的平稳序列。
library(TTR)
ma_12 <- SMA(AirPassengers, n=12)
plot(AirPassengers, main="12期简单移动平均", col="grey")
lines(ma_12, col="blue", lwd=2)
📌 指数平滑法
利用递减权重对历史数据赋予不同的重要性,近期数据权重更高,能更灵敏反映趋势。
exp_smooth <- HoltWinters(AirPassengers, beta=FALSE, gamma=FALSE)
plot(exp_smooth)
3.2 趋势型序列预测
📌 线性趋势模型
利用时间变量构建线性回归模型,预测未来走势,适用于单趋势线性增长或下降序列。
time <- time(AirPassengers)
model_lm <- lm(AirPassengers ~ time)
plot(AirPassengers, main="线性趋势预测", col="grey")
abline(model_lm, col="blue", lwd=2)
📌 非线性趋势模型(二次趋势)
在数据存在加速增长或非线性变化时,采用多项式回归更为贴切,如二次趋势模型。
model_quad <- lm(AirPassengers ~ time + I(time^2))
plot(AirPassengers, main="二次趋势预测", col="grey")
lines(fitted(model_quad), col="red", lwd=2)
3.3 复合型序列预测
📌 Holt-Winters季节平滑法
同时平滑趋势与季节成分,适用于包含趋势与季节性的序列,分为加法型与乘法型两种形式。
model_hw <- HoltWinters(AirPassengers)
plot(model_hw)
👉 预测未来12个月:
library(forecast)
forecast_hw <- forecast(model_hw, h=12)
plot(forecast_hw)
📌 ARIMA模型
综合自回归(AR)、差分(I)与移动平均(MA)模型,适用于一般非平稳时间序列,通过差分平稳化后建模。
library(forecast)
model_arima <- auto.arima(AirPassengers)
summary(model_arima)
forecast_arima <- forecast(model_arima, h=12)
plot(forecast_arima)
✅ 方法总结对比表
| 方法 | 适用情况 | 特点 |
|---|---|---|
| 简单平均法 | 平稳无趋势 | 算法简单,适合短期预测 |
| 移动平均法 | 平稳/波动序列 | 平滑噪声,提取趋势成分 |
| 指数平滑法 | 短期预测,平稳序列 | 权重递减,更关注近期数据 |
| 线性趋势 | 单趋势型序列 | 简单直观,线性拟合 |
| 二次/非线性趋势 | 加速增长或复杂趋势 | 拟合灵活,适应性强 |
| Holt-Winters季节平滑法 | 趋势+季节型序列 | 同时平滑趋势与季节性,稳定性强 |
| ARIMA模型 | 一般非平稳序列 | 功能强大,残差可检验,预测准确 |
四、时间序列分解案例
在时间序列分析中,许多实际问题涉及到数据随时间的长期趋势、周期性变化、季节性波动以及随机扰动的相互叠加。为了深入理解这些成分的结构,常常需要将时间序列分解为几个组成部分进行单独分析。时间序列分解方法能够有效揭示数据内在规律,为建模、预测、异常检测等提供理论依据和实践基础。
📑 数据集简介
采用R语言自带的经典航空客运数据集AirPassengers,该数据集记录了1949年至1960年,每月美国国际航空公司客运量(单位:千人),共144个观测值。此数据不仅具有明显的趋势性增长特征,还存在显著的季节性波动,非常适合用作时间序列分解的案例。
📊 分解原理
时间序列通常由以下三部分组成:
- 趋势项(Trend):反映数据随时间推移的长期变动方向。
- 季节项(Seasonal):反映数据随季节、周期等规律性波动的部分。
- 随机项(Random/Irregular):指无法用趋势或季节性解释的短期随机扰动。
常见的分解模型包括:
- 加法模型: \(X_t = T_t + S_t + R_t\)
- 乘法模型: \(X_t = T_t \times S_t \times R_t\)
对于AirPassengers,由于其波动幅度随总体水平增加而扩大,选用乘法模型进行分解。
💻 R语言实现
我们先使用decompose()函数对数据进行乘法模型分解:
# 载入数据
data("AirPassengers")
# 查看数据基本信息
summary(AirPassengers)
plot(AirPassengers, main="AirPassengers 原始数据")
# 时间序列分解
ap_decomp <- decompose(AirPassengers, type="multiplicative")
# 自定义分解图,线条加粗3倍 (lwd=3)
par(mfrow=c(4,1), mar=c(2,4,2,2)) # 设置4行1列图形窗口
# 原始数据
plot(AirPassengers, main="AirPassengers 原始数据", col="black", lwd=3)
# 趋势部分
plot(ap_decomp$trend, main="趋势 (Trend)", col="blue", lwd=3)
# 季节部分
plot(ap_decomp$seasonal, main="季节性 (Seasonal)", col="darkgreen", lwd=3)
# 随机部分
plot(ap_decomp$random, main="随机 (Random)", col="red", lwd=3)
# 恢复默认图形布局
par(mfrow=c(1,1))
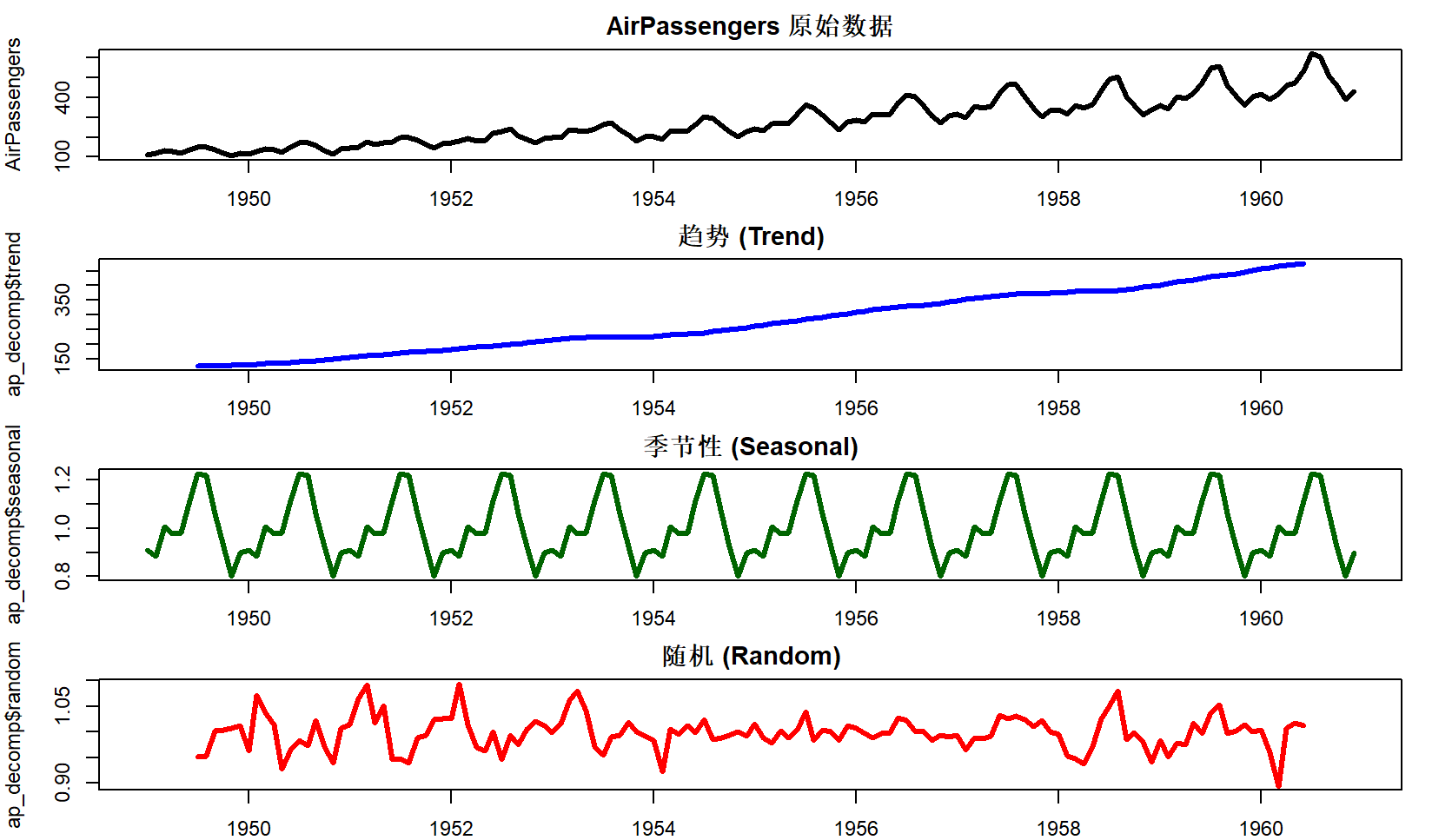
📈 分解结果解读
- 原始数据(Observed):
展示1949~1960年的航空客运量,客流量整体呈现递增趋势,且波动幅度随时间增加。 - 趋势项(Trend):
显示航空客运量长期稳定增长的趋势,尤其1954年以后增长速度加快,表明航空业迅速发展。 - 季节项(Seasonal):
每年6-8月为客流高峰期,12-2月为客流低谷,展现出强烈的季节性变化特征。 - 随机项(Random):
去除趋势和季节性因素后,剩余部分主要反映偶然性波动,大多数分布在1上下,说明分解效果良好。
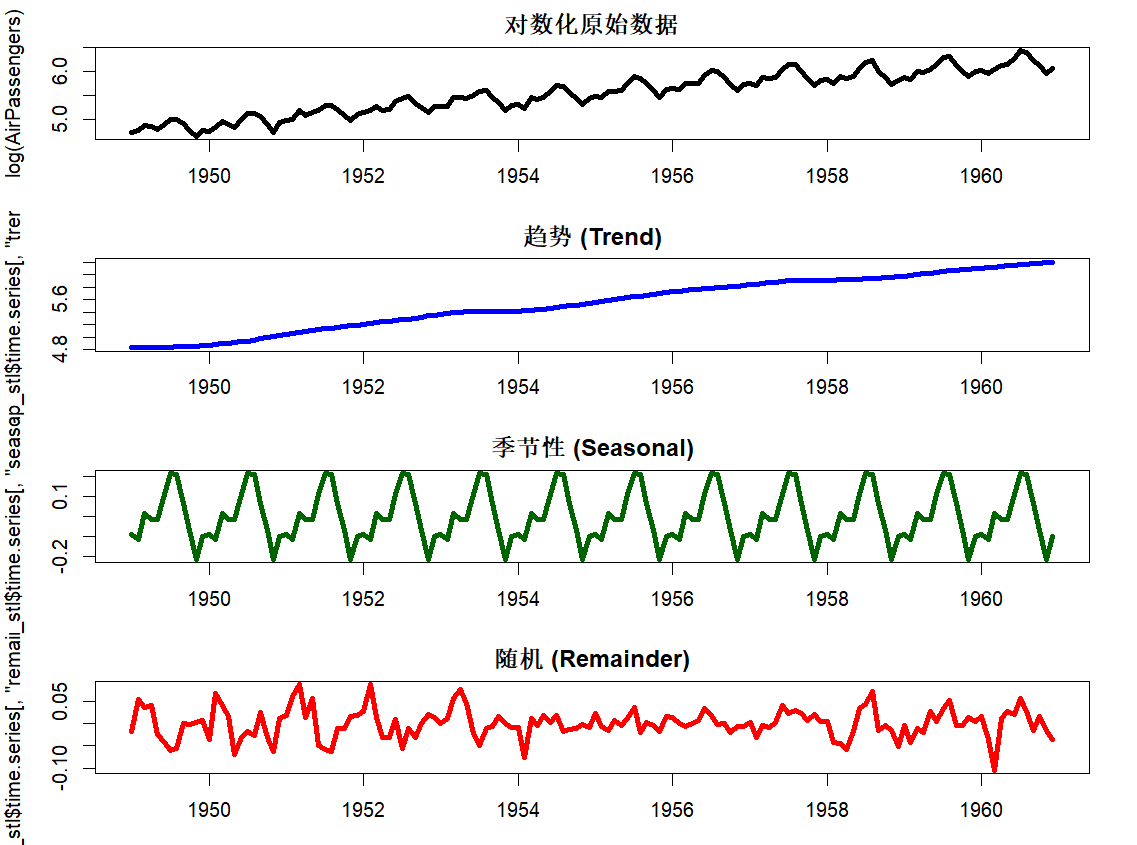
📊 STL分解法(更优方法)
除了decompose(),R中还提供了功能更强的stl()(Seasonal-Trend decomposition using Loess)方法,适用于非整数周期或趋势变动复杂的序列。
# 载入数据
data("AirPassengers")
# STL分解
ap_stl <- stl(log(AirPassengers), s.window="periodic")
# 设置图形布局:4行1列
par(mfrow=c(4,1), mar=c(3,4,2,2))
# 原始数据
plot(log(AirPassengers), main="对数化原始数据", col="black", lwd=3)
# 趋势部分
plot(ap_stl$time.series[,"trend"], main="趋势 (Trend)", col="blue", lwd=3)
# 季节部分
plot(ap_stl$time.series[,"seasonal"], main="季节性 (Seasonal)", col="darkgreen", lwd=3)
# 随机部分
plot(ap_stl$time.series[,"remainder"], main="随机 (Remainder)", col="red", lwd=3)
# 恢复默认设置
par(mfrow=c(1,1))
- log():对数据取对数,稳定方差。
- s.window="periodic":设定季节性平滑方式。
该方法利用LOESS局部加权回归进行趋势和季节成分提取,分解效果更平滑稳定,适合复杂序列。
📈 季节性调整
若希望得到去季节性的趋势数据,可按以下方法调整:
# 基于decompose分解结果的季节性调整
ap_season_adj <- AirPassengers / ap_decomp$seasonal
plot(ap_season_adj, main="去季节性后的航空客运量", col="darkgreen")
该图反映剔除季节性后的客运量走势,更准确描述长期趋势及随机波动特征。通过本案例可以清晰认识到:
- 时间序列分解能有效提取数据的趋势、季节性和随机波动部分。
- decompose()适合简单乘法或加法模型,stl()更适合复杂、非线性趋势数据。
- 分解结果有助于后续预测建模、异常值检测、趋势外推、季节调整等应用。
时间序列分解作为基础性分析步骤,是理解数据结构、提高预测精度的重要手段,广泛应用于经济、金融、市场营销、医疗、气象等众多领域。
结语
时间序列分析作为数据分析领域的重要分支,专注于研究数据随时间变化所呈现出的趋势性、周期性、季节性以及随机波动特性。与一般的横截面数据分析不同,时间序列不仅包含数值本身,更蕴含了时间序的结构性特征,若能合理提取其中的信息,不仅能够揭示变量演变的内在规律,还能对未来发展趋势做出科学预测。
在经济预测、市场决策、风险管理、生产调度、资源配置及自然现象模拟等领域,时间序列分析方法几乎无处不在。无论是政府部门制定宏观经济政策,企业分析销售走势,还是金融机构评估股票价格波动,时间序列模型都发挥着至关重要的作用。因此,掌握时间序列分析的基本方法与技巧,不仅是数据分析师的重要能力之一,也为各行各业的决策提供了坚实的数据依据和方法保障。



 浙公网安备 33010602011771号
浙公网安备 33010602011771号