二项分布、 Poisson 分布与正态分布

在概率论与数理统计领域，分布的概念是理解数据特征、进行建模与推断的基础，其中正态分布（Normal distribution）、二项分布（Binomial distribution）与泊松分布（Poisson distribution）是最为经典和常用的三种概率分布。这三类分布在数学性质、现实应用及彼此关系方面，都体现出重要的理论与实践价值。这里拟系统探讨这三种分布的概率形式、参数意义、应用情境及它们之间的近似关系与数学推导过程，进一步揭示其在实际建模与数据分析中的适用边界与相互转换机制，为深入理解概率统计奠定基础。

一、分布的数学表达

1.1 正态分布

正态分布是描述连续型随机变量的分布形式，它的概率密度函数为：

\[f(x) = \frac{1}{\sqrt{2\pi \sigma^2}} \exp\left( -\frac{(x - \mu)^2}{2\sigma^2} \right) \]

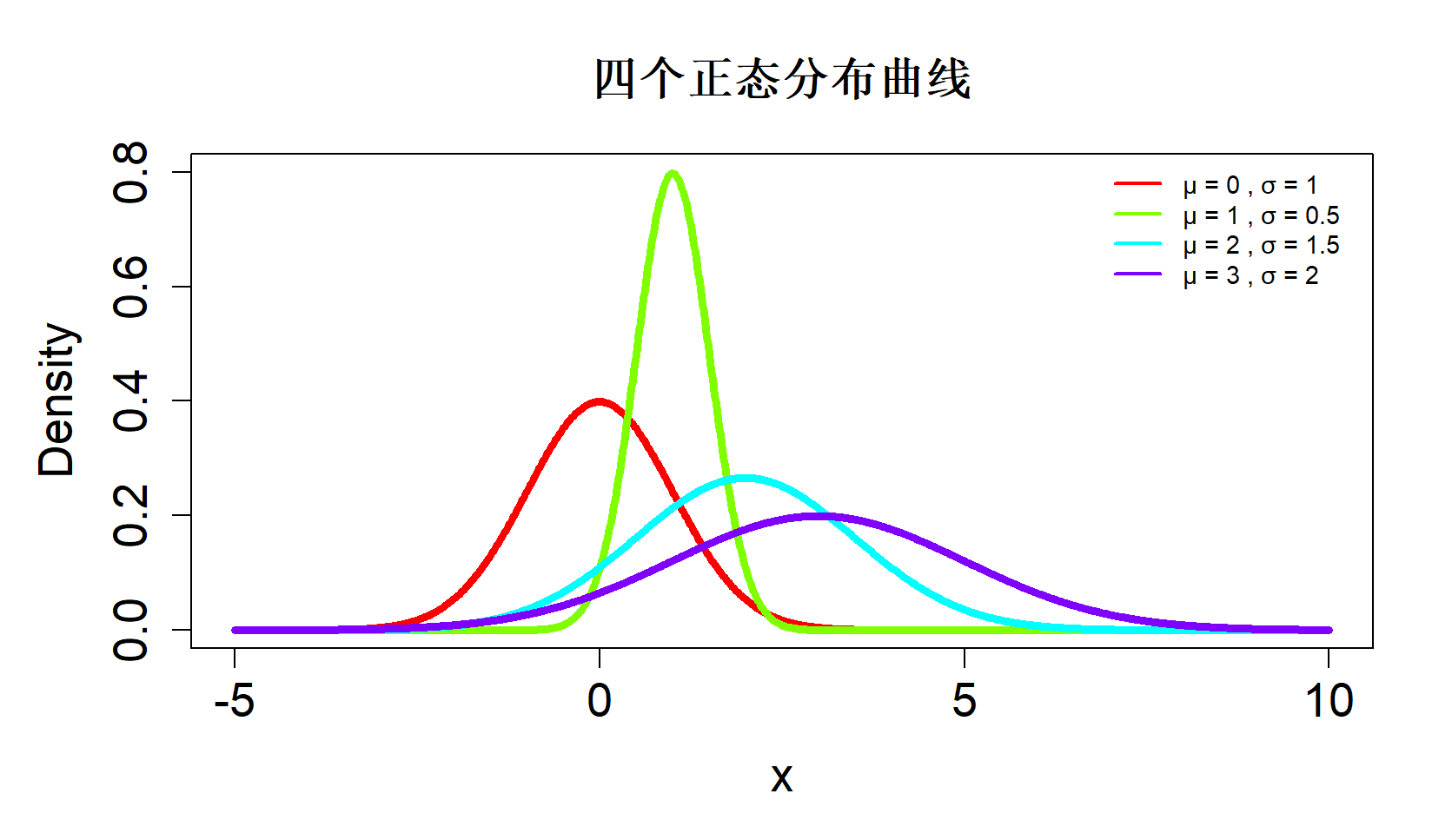
其中，\(\mu\) 为数学期望，\(\sigma^2\) 为方差。正态分布呈钟形曲线、关于 \(\mu\) 对称，是自然现象中最常见的分布类型之一。例如：身高、体重、考试成绩等变量常常服从或近似服从正态分布。
当 \(\mu=0\)、\(\sigma=1\) 时，称为标准正态分布，记作 \(Z \sim N(0,1)\)。

正态分布具有许多重要性质：

• 完全由均值和方差决定；
• 任意线性组合仍服从正态分布；
• 在中心极限定理下起核心作用；
• 在参数估计与假设检验中广泛应用。

# 设置参数
mu <- c(0, 1, 2, 3)  # 均值
sigma <- c(1, 0.5, 1.5, 2)  # 标准差
colors <- rainbow(length(mu))  # 每条曲线一种颜色

# x轴范围
x <- seq(-5, 10, length.out = 1000)

# 设置图形参数，增加图形尺寸
par(mar = c(5, 5, 4, 2) + 0.1)  # 设置边距
par(oma = c(0, 0, 0, 0))  # 设置外边距

# 绘制空白图
plot(x, dnorm(x, mean=mu[1], sd=sigma[1]), type="n",
     ylim=c(0, 0.8), xlab="x", ylab="Density",
     main="四个正态分布曲线",
     xlim=c(min(x), max(x)),  # 设置x轴范围
     cex.axis=1.5, cex.lab=1.5, cex.main=1.5)  # 增加坐标轴和标题的字体大小

# 添加每条正态分布曲线
for (i in seq_along(mu)) {
  y <- dnorm(x, mean=mu[i], sd=sigma[i])
  lines(x, y, col=colors[i], lwd=4)
}

# 添加图例
legend("topright", legend = paste("μ =", mu, ", σ =", sigma),
       col = colors, lwd = 2, cex = 0.8, bty = "n")  # 移除图例框

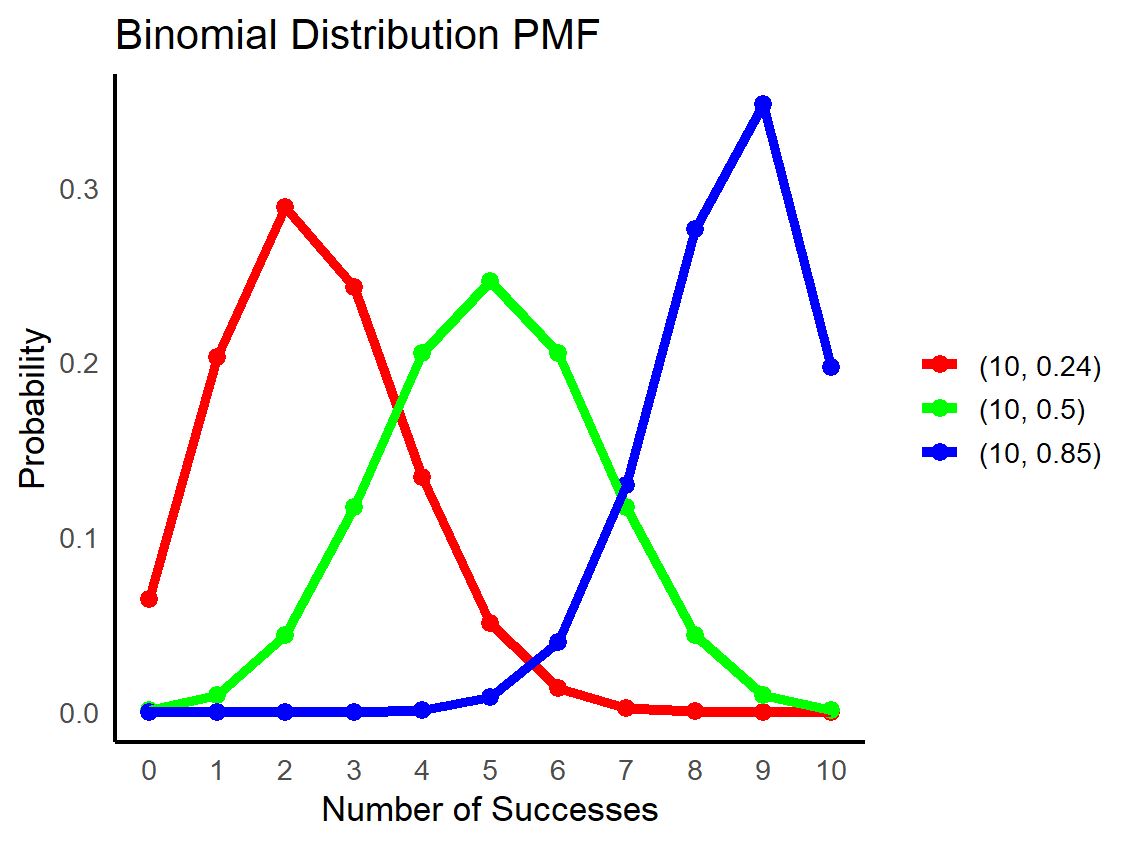
1.2 二项分布

二项分布用于刻画在固定次数的独立重复实验中，某事件成功出现的次数。其概率质量函数为：

\[P(X = k) = \binom{n}{k} \pi^k (1 - \pi)^{n - k}, \quad k = 0,1,2,\dots,n \]

其中：

• \(n\)：试验次数；
• \(\pi\)：每次试验中事件发生的概率；
• \(X\)：在 \(n\) 次试验中成功的次数。

举例来说，投掷一枚硬币 10 次，观察正面朝上的次数就是二项分布问题，若 \(\pi=0.5\)，则该分布对称。

二项分布的数学期望与方差如下：

\[E(X) = n\pi,\quad Var(X) = n\pi(1 - \pi) \]

二项分布是离散型分布，常用于概率估计、抽样检验、产品质量控制等领域。

# 加载绘图包
library(ggplot2)

# 参数设置
params <- list(c(10, 0.24), c(10, 0.5), c(10, 0.85))
colors <- c('red', 'green', 'blue')
labels <- c('(10, 0.24)', '(10, 0.5)', '(10, 0.85)')

# 构建数据框用于ggplot
data_list <- list()
for (i in 1:length(params)) {
  n <- params[[i]][1]
  p <- params[[i]][2]
  x <- 0:n
  prob <- dbinom(x, n, p)
  df <- data.frame(x = x, prob = prob, group = labels[i], color = colors[i])
  data_list[[i]] <- df
}
final_df <- do.call(rbind, data_list)

# 绘图（加粗线条、去掉网格、添加坐标轴）
ggplot(final_df, aes(x = x, y = prob, color = group)) +
  geom_point(size = 3) +                    # 点更大
  geom_line(size = 2) +                     # 线更粗
  scale_color_manual(values = colors) +
  labs(title = "Binomial Distribution PMF",
       x = "Number of Successes",
       y = "Probability") +
  theme_minimal(base_size = 14) +
  theme(
    legend.title = element_blank(),
    panel.grid = element_blank(),          # 去掉网格线
    axis.line = element_line(color = "black", size = 0.8),  # 添加坐标轴线
    axis.line.x = element_line(),          # 明确启用 X 轴线
    axis.line.y = element_line()           # 明确启用 Y 轴线
  ) +
  scale_x_continuous(breaks = 0:10)

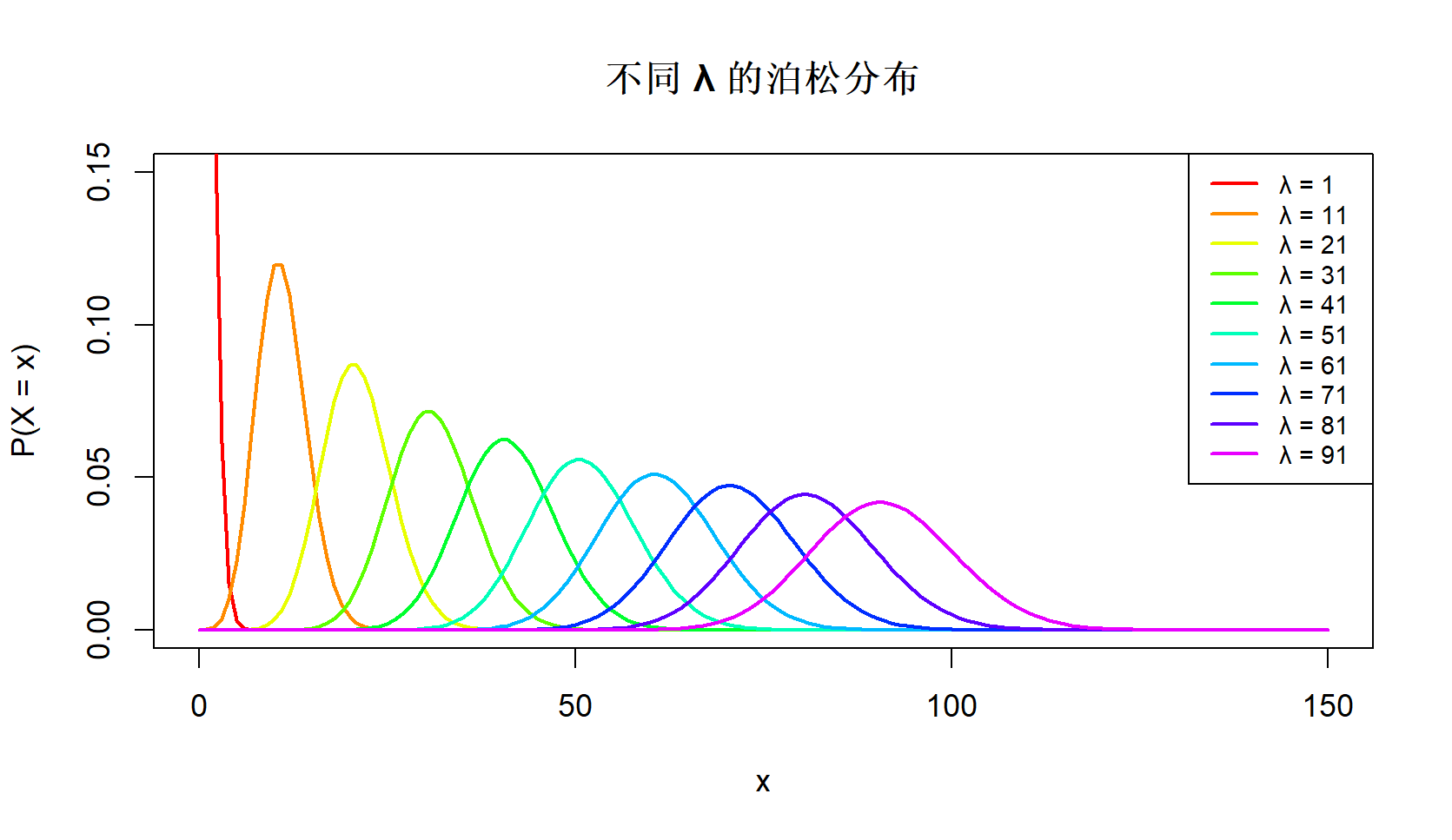
1.3 Poisson 分布

Poisson分布是一种单参数的离散分布，主要用于建模在单位时间或空间内某事件发生的次数，特别适合描述随机独立且稀疏发生的事件，如电话呼入、突发事故、网页点击等。

其概率质量函数为：

\[P(X = k) = \frac{\lambda^k e^{-\lambda}}{k!}, \quad k = 0,1,2,\dots \]

其中：

• \(\lambda > 0\) 为事件在单位时间或空间的平均发生次数；
• 期望与方差均为 \(\lambda\)：即 \(E(X) = Var(X) = \lambda\)。

Poisson分布适用于“低概率高频率”的情形，如工业产品缺陷检测、交通流量建模、医疗应急预测等。

# 设置图形参数
colors <- rainbow(11)  # 设置不同颜色，共11种 λ 值
lambdas <- seq(1, 100, by = 10)  # λ 从1到100，间隔10
x <- 0:150  # x轴从0到150

# 画空图框
plot(x, dpois(x, lambda=1), type="n", ylim=c(0, 0.15),
     xlab="x", ylab="P(X = x)", main="不同 λ 的泊松分布")

# 添加每条 λ 曲线
for (i in seq_along(lambdas)) {
  lines(x, dpois(x, lambda = lambdas[i]), col = colors[i], lwd = 2)
}

# 添加图例
legend("topright", legend = paste("λ =", lambdas),
       col = colors, lwd = 2, cex = 0.8)

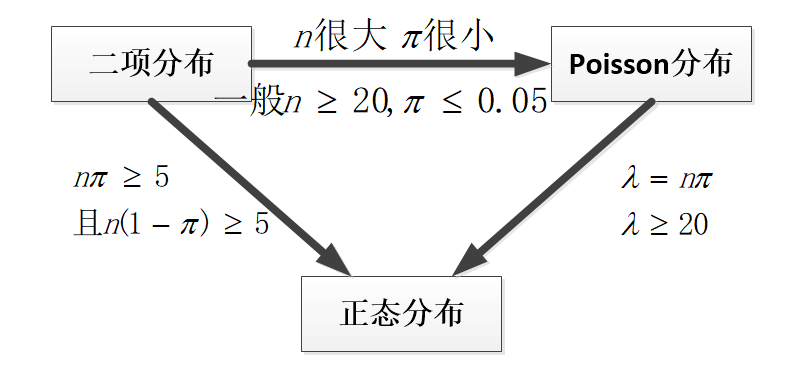
二、分布之间的近似关系

在统计建模与概率推导过程中，三个分布并非孤立存在，而是可以在特定条件下相互近似替代。最常见的两类近似关系如下：

2.1 二项分布近似正态分布（De Moivre-Laplace定理）

当试验次数 \(n\) 较大，且事件发生概率 \(\pi\) 不过于接近 0 或 1 时，二项分布 \(B(n,\pi)\) 可近似为正态分布：

\[B(n,\pi) \approx N(n\pi,n\pi(1-\pi)) \]

更精确的近似形式包括连续性修正：

\[P(X = k) \approx \Phi\left( \frac{k + 0.5 - n\pi}{\sqrt{n\pi(1 - \pi)}} \right) - \Phi\left( \frac{k - 0.5 - n\pi}{\sqrt{n\pi(1 - \pi)}} \right) \]

该定理是中心极限定理的早期具体表达，广泛应用于大样本近似分析。

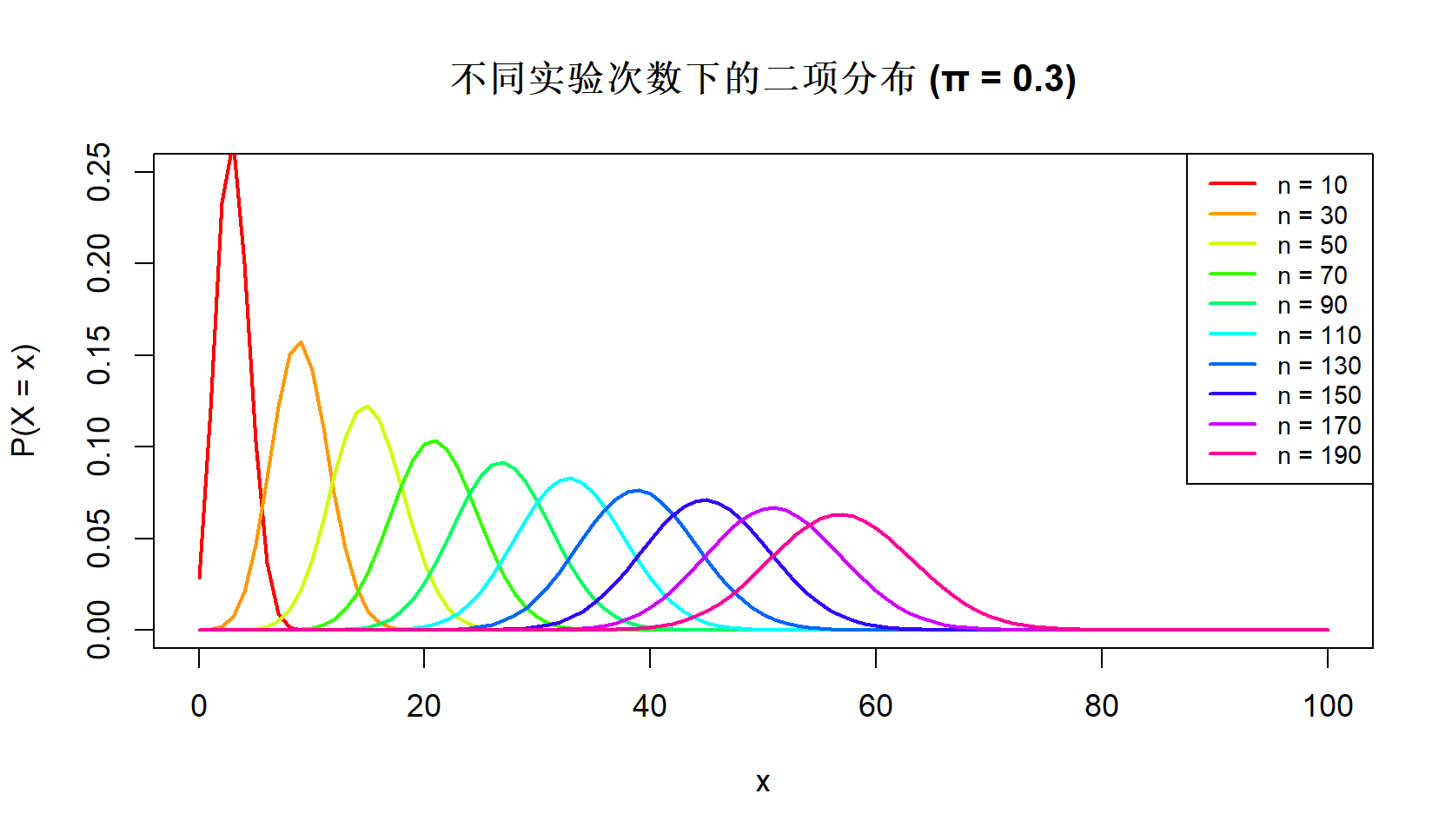
# 设置参数
prob <- 0.3  # 成功概率
trials <- seq(10, 200, by = 20)  # 实验次数从10到200，间隔20
colors <- rainbow(length(trials))  # 每条曲线一种颜色

# x轴范围改为0到100
x <- 0:100

# 绘制空白图
plot(x, dbinom(x, size=trials[1], prob=prob), type="n",
     ylim=c(0, 0.25), xlab="x", ylab="P(X = x)",
     main="不同实验次数下的二项分布 (π = 0.3)")

# 添加每条二项分布曲线
for (i in seq_along(trials)) {
  y <- dbinom(x, size=trials[i], prob=prob)
  lines(x, y, col=colors[i], lwd=2)
}

# 添加图例
legend("topright", legend = paste("n =", trials),
       col = colors, lwd = 2, cex = 0.8)

2.2 二项分布近似 Poisson 分布（Poisson 极限定理）

当 \(n\) 很大，\(\pi\) 很小，且保持 \(\lambda = n\pi\) 恒定时，二项分布趋于 Poisson 分布：

\[\lim_{n \to \infty} \binom{n}{k} \pi^k (1 - \pi)^{n - k} = \frac{\lambda^k e^{-\lambda}}{k!} \]

即：

\[B(n,\pi) \to P(\lambda) \]

这种情形适用于大量独立小概率事件的建模，例如罕见病发生次数、网络攻击等。

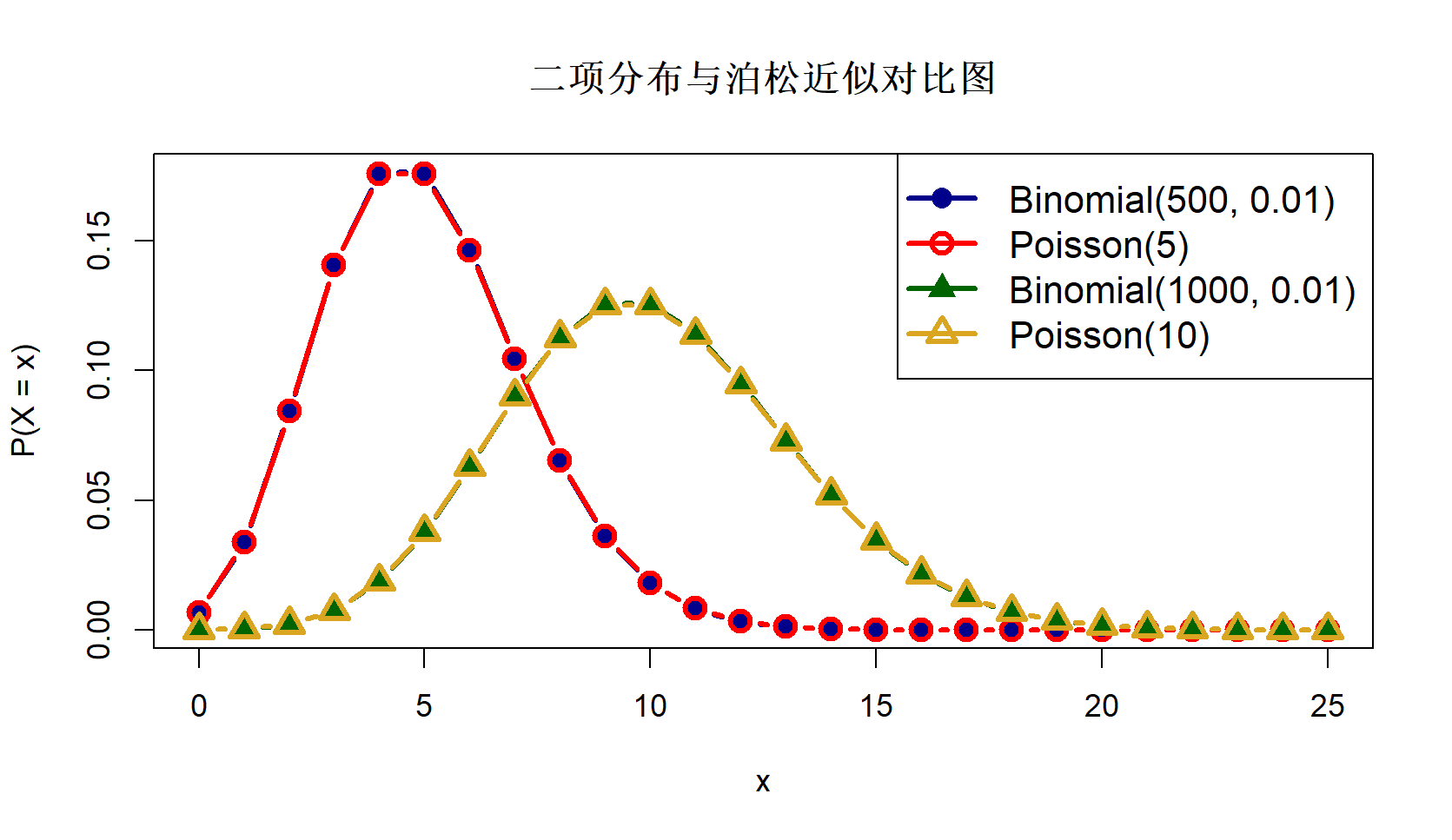
# 设置参数
prob <- 0.3  # 成功概率
trials <- seq(10, 200, by = 20)  # 实验次数从10到200，间隔20
colors <- rainbow(length(trials))  # 每条曲线一种颜色

# x轴范围改为0到100
x <- 0:100

# 绘制空白图
plot(x, dbinom(x, size=trials[1], prob=prob), type="n",
     ylim=c(0, 0.25), xlab="x", ylab="P(X = x)",
     main="不同实验次数下的二项分布 (p = 0.3)")

# 添加每条二项分布曲线
for (i in seq_along(trials)) {
  y <- dbinom(x, size=trials[i], prob=prob)
  lines(x, y, col=colors[i], lwd=2)
}

# 添加图例
legend("topright", legend = paste("n =", trials),
       col = colors, lwd = 2, cex = 0.8)

2.3 Poisson 分布近似正态分布

Poisson分布虽然是离散的，但当其参数 \(\lambda\) 足够大（通常认为 \(\lambda \geq 20\)）时，形状趋于对称，可用正态分布近似：

\[P(\lambda) \approx N(\lambda,\lambda) \]

引入连续性修正后，有：

\[P(X = k) \approx \Phi\left( \frac{k + 0.5 - \lambda}{\sqrt{\lambda}} \right) - \Phi\left( \frac{k - 0.5 - \lambda}{\sqrt{\lambda}} \right) \]

这种近似在交通、服务系统、排队模型等领域广泛应用。

三种分布的形态因参数取值不同而有所差异：

分布类型	参数	图形特征	是否对称
正态分布	\(\mu,\sigma^2\)	钟形曲线、连续平滑	是
二项分布	\(n=20,\pi=0.5\)	近似对称、离散分布	是
二项分布	\(n=1000,\pi=0.01\)	偏态、接近泊松	否
Poisson分布	\(\lambda=3\)	偏右、不对称	否
Poisson分布	\(\lambda=30\)	接近正态、对称	是

随着参数变化，二项分布和泊松分布均能在不同条件下近似正态分布。这种图形演化也直观说明了它们间的连续性。

三、现实应用

概率分布模型并非仅用于理论推导，更在现实生活与工业实践中广泛应用。以下将围绕工业质量控制、医疗应急预测、通信流量管理与金融风控四个典型场景，说明正态分布、二项分布与泊松分布的适用情境与数学处理方式。

3.1 工业质量控制

在制造业中，控制产品质量是保证产出稳定性的关键任务。设某工厂生产的零件平均每100件中有1件为不合格品。若每天产出1000件，则每天出现的次品数 \(X\) 可建模为：

\[X \sim B(n=1000, \pi=0.01) \]

此时：

• 期望值：\(E(X) = n\pi = 10\)；
• 方差：\(\mathrm{Var}(X) = n\pi(1 - \pi) = 9.9\)。

由于试验次数 \(n\) 较大，且次品率 \(\pi\) 很小，我们可用Poisson分布进行近似：

\[X \approx P(\lambda = 10) \]

进一步考虑到 \(\lambda = 10\) 也不算太小，且公司希望快速判断每日次品是否“异常”，此时可以使用正态分布进行连续性近似：

\[X \approx N(10, 10) \]

举例而言，若一天检测出15件次品，使用标准正态分布估算其偏离程度：

\[Z = \frac{15 - 10}{\sqrt{10}} \approx 1.58 \]

查正态表得：\(P(Z > 1.58) \approx 0.0571\)，说明约有5.7%的概率出现更糟的情况。管理者可据此决定是否进行设备检修或工序调整。

此外，若希望控制次品率低于某阈值（如次品数不超过12件），可用正态累计分布函数估算合格概率，从而制定质量预警系统。

3.2 医疗应急预测

医院急诊科需合理安排人力资源应对不同时间段的就诊需求。若观察数据发现某医院急诊平均每小时接收30位患者，设到达过程独立随机，适合建模为：

\[X \sim P(\lambda = 30) \]

此时：

• 期望值与方差均为30；
• 可判断病人到达为典型的泊松过程。

若医院希望估算“每小时到达人数在25到35人之间”的概率，可使用正态分布进行近似：

\[X \approx N(30, 30) \]

引入连续性修正，有：

\[P(25 \leq X \leq 35) \approx P(24.5 < X < 35.5) \]

标准化处理：

\[Z_1 = \frac{24.5 - 30}{\sqrt{30}} \approx -1.00,\quad Z_2 = \frac{35.5 - 30}{\sqrt{30}} \approx 1.00 \]

查表得：

\[P(-1.00 < Z < 1.00) \approx 0.6826 \]

即，医院在超过68%的小时中会接待25到35位病人，可以据此安排轮班制度和预警机制。若期望覆盖 95% 情况，可按 \(\pm 2\sigma\) 设置响应能力。

3.3 通信与网络流量管理

在通信系统中，如服务器处理请求、网络中断事件、短信发送等，常可抽象为单位时间内事件发生次数的建模。假设一台服务器平均每分钟处理 100 个请求，系统希望评估一分钟内高于120个请求是否为异常。

设：

\[X \sim P(\lambda = 100) \]

由于 \(\lambda\) 较大，可近似为：

\[X \approx N(100, 100) \]

则：

\[Z = \frac{120 - 100}{\sqrt{100}} = 2 \]

查标准正态表可知：

\[P(Z > 2) \approx 0.0228 \]

即只有约2.3%的概率出现“一分钟请求数高于120”的情况，系统可将此作为性能瓶颈报警点。若超过此值频繁发生，则说明服务器需扩容或流量需负载均衡处理。

3.4 金融风控场景

金融风控中，例如信用卡欺诈检测、股票价格波动建模等，也常使用正态或二项模型。在某信用卡用户群中，欺诈交易发生概率为千分之一，若系统一天检测10万笔交易，建模为：

\[X \sim B(100000, 0.001) \]

• 期望为100；
• 因 \(n\) 大、\(\pi\) 小，可近似为 \(P(100)\)；
• 若 \(\lambda = 100\) 更大，可进一步近似为 \(N(100, 100)\)。

系统可计算当天欺诈交易超过某值的概率，进而设定风控阈值、审计标准等。

四、理论基础：中心极限定理统一三类分布

在概率论与数理统计中，中心极限定理（Central Limit Theorem, CLT）是描述大数集合规律性的重要支柱。它指出：当一组独立同分布的随机变量 \(X_1, X_2, \ldots, X_n\)，具有期望 \(\mu\) 和有限方差 \(\sigma^2\)，则其标准化和：

\[Z_n = \frac{\sum_{i=1}^n X_i - n\mu}{\sqrt{n\sigma^2}} \xrightarrow{d} N(0,1) \]

即：当 \(n \to \infty\) 时，这类随机变量的和服从标准正态分布。这条定理不仅揭示了正态分布的普适性，也奠定了其在自然现象建模中的核心地位。

4.1 二项分布的正态近似

二项分布本质上是 \(n\) 个独立的伯努利试验之和，每个试验结果为“成功”或“失败”。设每次试验成功概率为 \(\pi\)，则总成功次数：

\[X = \sum_{i=1}^{n} X_i,\quad X_i \sim \text{Bernoulli}(\pi) \]

此时 \(E(X) = n\pi,\ \mathrm{Var}(X) = n\pi(1 - \pi)\)。当 \(n\) 足够大时，根据中心极限定理：

\[X \approx N(n\pi,\ n\pi(1 - \pi)) \]

这就是我们熟知的二项分布的正态近似，常在质量控制、抽样检验中被广泛使用。需要注意的是，常以 \(np \geq 5\) 且 \(n(1 - p) \geq 5\) 为近似合理性条件，并进行连续性修正。

4.2 Poisson 分布的正态近似

Poisson 分布描述单位时间/空间中稀疏独立事件的出现次数，如顾客到达、事故发生等。设事件平均发生率为 \(\lambda\)，则：

\[X \sim P(\lambda),\quad E(X) = \lambda,\quad \mathrm{Var}(X) = \lambda \]

当 \(\lambda\) 足够大时，泊松分布也可近似为正态分布：

\[X \approx N(\lambda,\ \lambda) \]

这是由于 Poisson 分布亦可看作大量小概率二项事件（极限情况）的和。例如当 \(n \to \infty,\ p \to 0\)，且 \(np = \lambda\) 固定时：

\[B(n,p) \xrightarrow{d} P(\lambda) \]

再由中心极限定理，得 Poisson 的正态近似。通常认为 \(\lambda \geq 10\) 时近似效果良好。

由此可见，无论是二项分布还是 Poisson 分布，其在样本量大或事件频率升高的极限下，都可以借助中心极限定理统一为正态模型。这一现象揭示了随机现象中“个体差异可被群体规律所消解”的深层数学原理，是统计推断和大数据建模中不可或缺的理论支撑。

总结

正态分布、二项分布与泊松分布构成了概率分布的“三驾马车”，在理论与实践中均有重要地位。它们之间的相互近似使我们在处理不同类型数据时能够灵活建模、互通有无。

• 正态分布：理论基石，应用广泛；
• 二项分布：抽样估计与概率论的重要工具；
• Poisson分布：描述低频稀疏事件的利器；
• 三者之间可通过极限定理、中心极限定理建立桥梁，实现跨分布推理；
• 在实际建模中需结合参数条件、变量特性、近似精度等要素合理选择分布模型。

在大数据、人工智能快速发展的背景下，经典分布理论仍旧在现代算法中充当基础角色。掌握这些核心分布，有助于构建起严密的数学分析思维框架，并提升应对复杂问题的建模与推理能力。

参考文献

1. 泊松分布 二项分布 正态分布之间的联系
2. 二项分布、泊松分布、正态分布的关系