结构化编程设计——复杂系统模式（输入输出）的展现

结构化程序设计（Structured Programming）是由荷兰计算机科学家Edsger W. Dijkstra在1968年发表的论文《Go To Statement Considered Harmful》中首次提出的。Dijkstra 认为，程序中的“goto”语句会导致程序流程的混乱，增加调试和维护的难度。为了解决这一问题，Dijkstra 提出了通过顺序结构、选择结构和循环结构三种基本结构来替代“goto”语句，构建清晰的程序控制流。在这一理论基础上，程序的单一入口和单一出口（Single Entry, Single Exit，简称 SESE）原则成为结构化程序设计的重要规范，即复杂系统模式设计思路。Python 作为一种高级语言，天然支持结构化程序设计的范式，接下来将分别阐述结构化程序的三种基本结构，并通过 Python 代码示例进行展现。

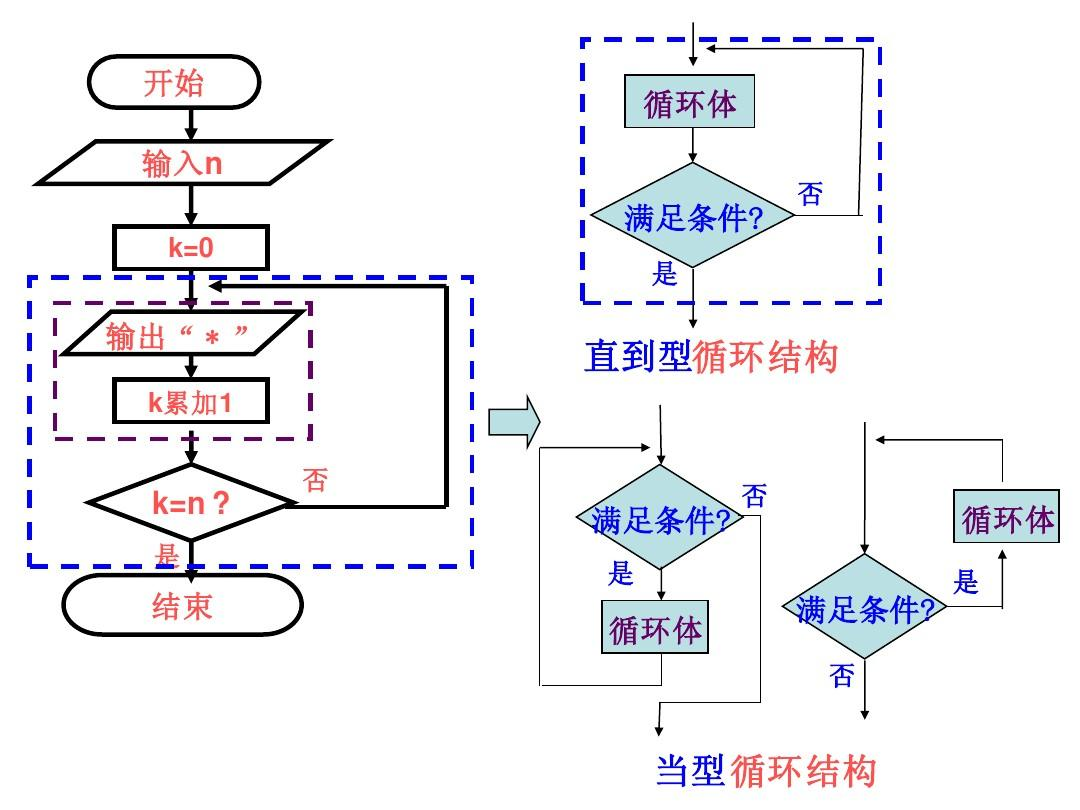
一、结构化程序设计的支撑理论

单一入口和单一出口（Single Entry, Single Exit，SESE）原则作为结构化程序设计的重要规范，主要得到了以下理论的支撑：

1.1. Dijkstra 的“Goto 语句有害”理论（1968）

• 论文：《Go To Statement Considered Harmful》（1968）
• 作者：Edsger W. Dijkstra
• 核心观点：
  • Dijkstra 指出“goto”语句会导致程序流程的跳转混乱，使程序的可读性和可维护性降低。
  • 他主张通过顺序结构、选择结构和循环结构取代“goto”，使程序的控制流程变得清晰和可预测。
  • Dijkstra 的理论为“单一入口、单一出口”奠定了基础，因为只有在这种结构下，程序的逻辑才能保持一致性和清晰度。

---

1.2. Böhm-Jacopini 定理（1966）

• 论文：《Flow Diagrams, Turing Machines and Languages with Only Two Formation Rules》（1966）
• 作者：Corrado Böhm 和 Giuseppe Jacopini
• 核心观点：

  • Böhm-Jacopini 定理证明了：

    任何程序都可以通过仅使用顺序结构、选择结构和循环结构来实现，且不需要使用“goto”语句。

  • 该定理从理论上证明了：单一入口、单一出口的程序构造方式是完备的，能够表达任意的算法。

  • 该定理为结构化程序设计的普适性提供了数学证明。

---

1.3. Mills 的结构化设计理论（1971）

• 论文：《Structured Programming: Retrospect and Prospect》（1971）
• 作者：Harlan D. Mills
• 核心观点：
  • Mills 提出程序设计应该采用封装和模块化的方式，每个模块都应该具有单一入口和单一出口。
  • 强调使用模块化和层次化的设计方式来增强程序的可理解性和可维护性。
  • Mills 的观点进一步推广了 Dijkstra 和 Böhm-Jacopini 的理论，提出程序在结构化基础上可以通过模块化提升复杂系统的可管理性。

---

1.4. McCabe 的圈复杂度理论（1976）

• 论文：《A Complexity Measure》（1976）

• 作者：Thomas J. McCabe

• 核心观点：

  • McCabe 提出了**圈复杂度（Cyclomatic Complexity）**的概念，用于衡量程序的复杂度。
  • 公式：
  \[V(G) = E - N + 2P \]

其中：
- V(G) = 圈复杂度
- E = 控制流图中的边数
- N = 控制流图中的节点数
- P = 控制流图的连通分量数
- McCabe 发现，程序的复杂度与其分支和循环数量密切相关。单一入口和单一出口可以有效降低圈复杂度，从而提高程序的可维护性和可测试性。

---

1.5. Hoare 的程序正确性理论（1969）

• 论文：《An Axiomatic Basis for Computer Programming》（1969）

• 作者：Tony Hoare

• 核心观点：

  • Hoare 提出了著名的Hoare 逻辑，用于形式化地证明程序的正确性。
  • Hoare 逻辑基于三元组：
    \[\{P\}C\{Q\} \]

其中：
- P = 前置条件
- C = 代码块
- Q = 后置条件
- 单一入口和单一出口可以使得 Hoare 逻辑的推导更加直观和严谨，有助于通过形式化方法验证程序的正确性。

---

1.6. Jackson 结构化程序设计方法（1975）

• 书籍：《Principles of Program Design》（1975）
• 作者：Michael A. Jackson
• 核心观点：
  • Jackson 提出了**Jackson 结构化程序设计（JSP）**方法，强调程序结构与数据结构的一致性。
  • 通过单一入口和单一出口，可以将程序映射为清晰的数据结构，从而增强程序的模块化和可理解性。

理论来源	时间	核心贡献	对 SESE 原则的支持
Dijkstra 的“Goto有害”理论	1968	反对“goto”，强调结构化编程	促进结构化设计，避免跳转混乱
Böhm-Jacopini 定理	1966	证明三种基本结构的完备性	证明SESE原则是完备的
Mills 结构化设计理论	1971	强调模块化和层次化	单一入口和出口促进模块化
McCabe 圈复杂度理论	1976	提出圈复杂度公式	SESE有助于降低圈复杂度
Hoare 程序正确性理论	1969	提出 Hoare 逻辑	SESE 有助于形式化证明
Jackson 结构化程序设计方法	1975	强调数据与结构的一致性	SESE 有助于映射数据结构
Liskov 抽象数据类型理论	1974	定义抽象数据类型	SESE 符合封装和接口设计
Parnas 模块化理论	1972	强调模块独立性	SESE 有助于模块独立性

二、结构化程序设计的特点

结构化程序设计（Structured Programming）是现代程序设计的重要范式，其核心是通过顺序结构、选择结构和循环结构来实现清晰的程序流程。结构化程序设计强调程序的可理解性、可维护性和可扩展性，遵循“单一入口与单一出口”（SESE）原则。以下是结构化程序设计的五个重要特点：

2.1. 模块化（Modularity）

模块化是结构化程序设计的核心特征之一，指将程序划分为若干个相互独立但可以协同工作的模块。

• 每个模块完成特定的功能，具有独立的输入和输出接口。
• 通过模块之间的接口进行数据和信息的交换。
• 优势：
  • 提高程序的可读性和可维护性。
  • 便于调试和测试。
  • 促进代码复用，减少开发成本。

示例：

def add(a, b):
    return a + b

def multiply(a, b):
    return a * b

def main():
    x = add(2, 3)
    y = multiply(x, 4)
    print(y)

在上述示例中，add 和 multiply 是两个独立的模块，main 通过调用模块完成整体功能。

---

2.2. 自顶向下设计（Top-Down Design）

自顶向下设计指从整体结构出发，逐步细化和分解为具体模块，最终实现完整的程序。

• 先定义程序的总体目标。
• 将整体问题划分为若干个子问题。
• 逐步解决每个子问题，形成完整的程序。
• 优势：
  • 强化程序结构的清晰度。
  • 方便模块之间的协同和扩展。

示例：

def main():
    data = read_data()
    result = process_data(data)
    output_result(result)

程序通过main函数组织各个模块，遵循“自顶向下”的流程设计。

---

2.3. 结构化控制（Structured Control）

结构化程序设计遵循三种基本的控制结构：

• 顺序结构：按既定的顺序执行代码块。
• 选择结构：根据条件选择不同的执行路径（如if-else结构）。
• 循环结构：在满足条件时重复执行代码块（如for或while结构）。
• 优势：
  • 避免了“goto”带来的跳转混乱。
  • 提高程序的可预测性和可理解性。

示例：

def check_even(num):
    if num % 2 == 0:
        return "Even"
    else:
        return "Odd"

在上述示例中，if-else 结构清晰地展示了选择结构的特性。

---

2.4. 局部化（Localization）

局部化指在模块内部定义和管理变量，限制其作用范围，避免模块之间的相互影响。

• 每个模块中的变量是局部变量，在模块外部不可访问。
• 通过参数和返回值进行模块间的数据交换。
• 优势：
  • 减少变量命名冲突和数据污染。
  • 便于调试和模块独立测试。

示例：

def calculate_area(length, width):
    area = length * width
    return area

在上述示例中，length、width 和 area 都是局部变量，仅在calculate_area模块内有效。

---

2.5. 可重用性或嵌套（Reusability）

结构化程序设计中的模块具有独立性和封装性，可以在不同场景下直接复用。

• 通过参数传递增强模块的灵活性。
• 通过封装减少对内部实现细节的依赖。
• 优势：
  • 提高开发效率。
  • 便于扩展和维护。

示例：

def add(a, b):
    return a + b

def multiply(a, b):
    return a * b

# 在不同程序中复用
result = add(5, 3)
result2 = multiply(result, 2)

在上述示例中，add 和 multiply 作为独立模块可以在其他程序中直接复用。

---

结构化程序设计通过模块化、自顶向下设计、结构化控制、局部化和可重用性，构建了清晰、稳定且易于维护的程序结构。这些特性提高了程序的可理解性和扩展性，奠定了现代程序设计的重要基础。

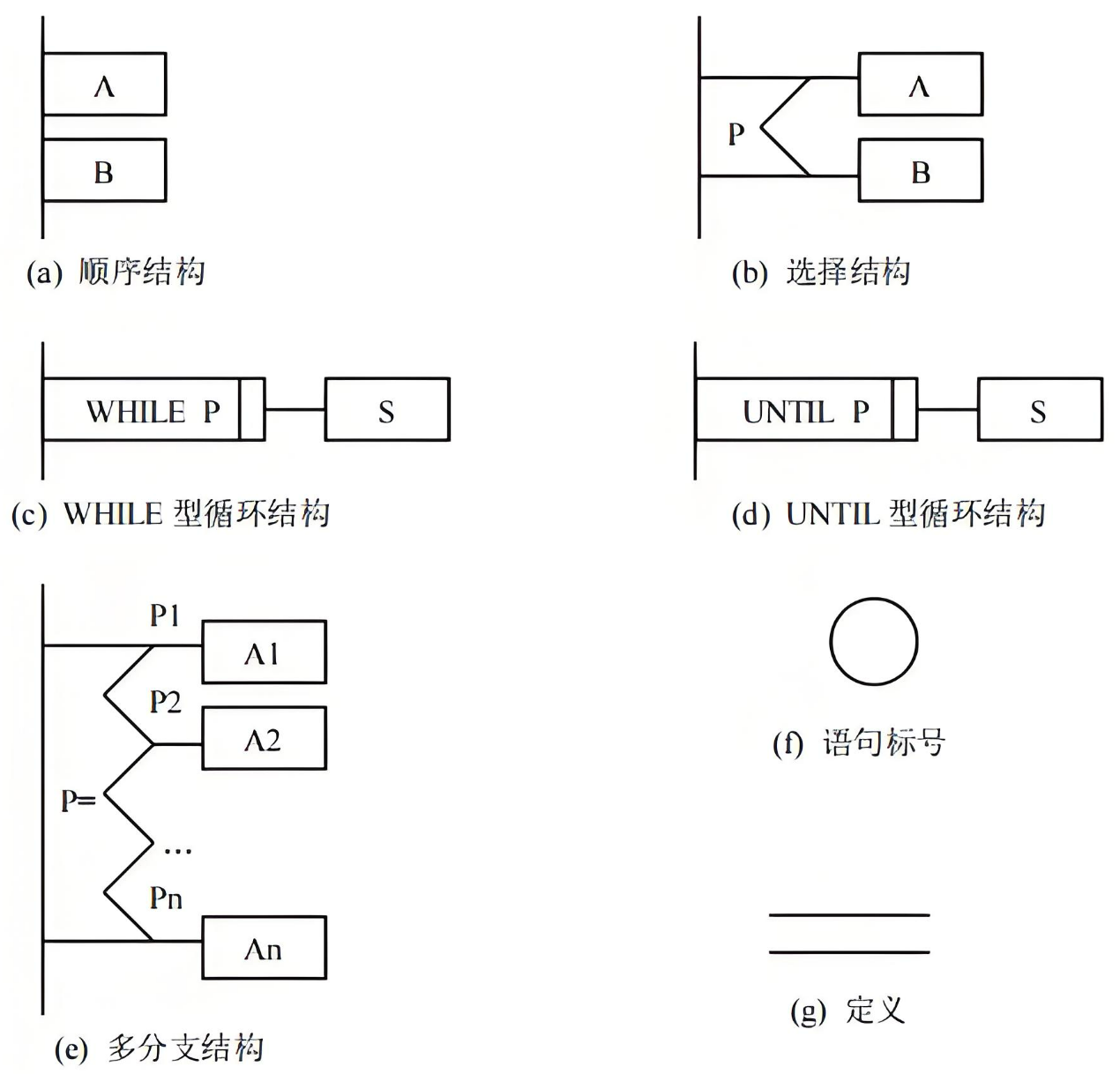
三、三种基本程序结构及 Python 示例

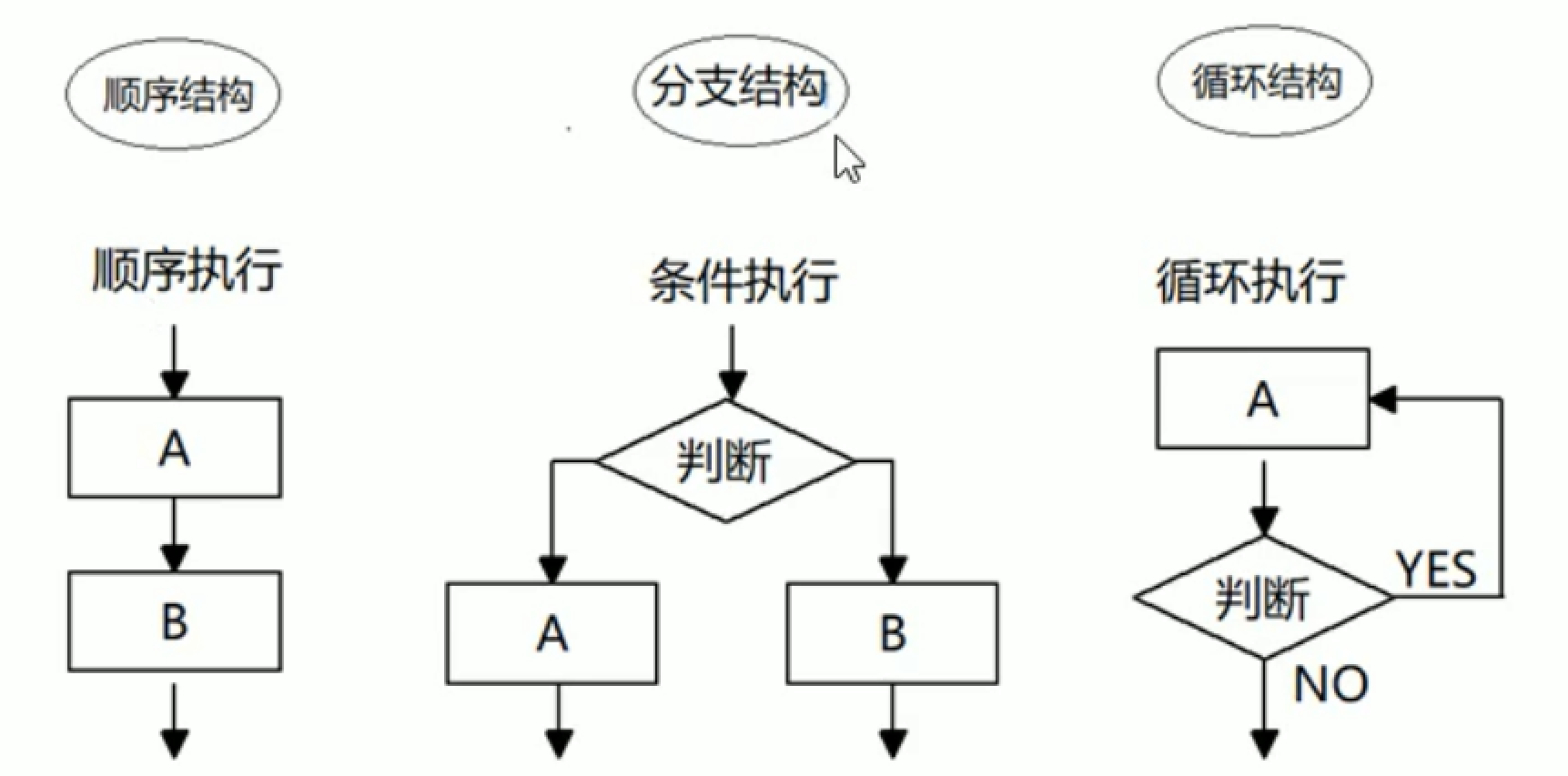
3.1. 顺序结构（Sequence）

顺序结构 是程序中最基本的执行方式，按照代码的书写顺序，从上到下依次执行每一条指令。

示例：计算两个数的和

# 定义两个变量
a = 5
b = 3
# 计算它们的和
sum = a + b
# 输出结果
print("Sum:", sum)

解释：
依次执行赋值、加法运算和输出操作。
代码按顺序依次执行，不涉及跳转和分支。

3.2. 选择结构（Selection）

选择结构 是根据条件的判断来决定程序的执行路径。常见的选择结构包括 if...else 和 if...elif...else。
示例：判断一个数是奇数还是偶数

# 输入一个整数
num = int(input("Enter a number: "))
# 判断奇偶性
if num % 2 == 0:
    print(f"{num} 是偶数")
else:
    print(f"{num} 是奇数")

解释：
使用 if...else 结构，根据条件 num % 2 == 0 判断，选择不同的执行路径。
如果条件成立，执行 if 块；否则执行 else 块。

3.3. 循环结构（Loop）

循环结构 用于在满足特定条件时重复执行某段代码，常见的循环包括 for 循环和 while 循环。
示例：用 for 循环计算前 10 个自然数的和

total = 0
for i in range(1, 11):
    total += i
print("Sum of first 10 natural numbers:", total)

示例：用 while 循环打印 1 到 5 的数字

i = 1
while i <= 5:
    print(i)
    i += 1

解释：
for 循环适用于已知循环次数的情况。
while 循环适用于在满足某个条件时重复执行代码。

3.4. 递归程序示例（整合三种基本结构）

递归是一种特殊的程序控制结构，它允许一个函数在其定义中调用自身。递归在本质上可以看作是通过 选择结构 和 顺序结构 来判断终止条件，通过 循环结构 来重复调用自身。
示例：用递归求解斐波那契数列

def fibonacci(n):
    if n <= 0:
        return 0
    elif n == 1:
        return 1
    else:
        return fibonacci(n - 1) + fibonacci(n - 2)
# 输出前 10 个斐波那契数
for i in range(10):
    print(fibonacci(i), end=" ")

解释：
顺序结构： 函数调用和返回值操作是顺序结构。
选择结构： 使用 if...elif...else 判断终止条件。
循环结构： 使用递归和 for 循环输出前 10 个斐波那契数。

总结

结构化程序设计通过顺序、选择和循环三种基本结构，能够构建出大部分复杂程序。

• 顺序结构 保证程序的逻辑性和执行顺序。
• 选择结构 增强程序的灵活性和智能性。
• 循环结构 实现重复性任务的自动化。
  递归程序是结构化程序设计的重要延伸，结合了三种基本结构的特点，能够简洁地解决复杂的递推问题。结构化程序设计不仅提高了代码的可读性和可维护性，也为程序的模块化和扩展性提供了坚实的基础。

框图	NS图或盒图	PAD图