纳什均衡——机器博弈的诠释

博弈作为人类智慧与策略的体现，自古以来便深刻影响着社会的发展和演化。从中国象棋到田忌赛马，博弈贯穿着人类文明的历史脉络，反映了竞争、合作与策略平衡的复杂性。在现代社会，商业竞争、军事对抗、市场博弈等场景无一不涉及博弈理论的深层逻辑。随着人工智能（AI）技术的飞速发展，人们开始思考：机器是否能够像人类一样参与博弈，并通过自主学习和策略优化，在复杂竞争环境中做出智能决策？
机器博弈（Machine Game）正是基于这一探索而发展起来的交叉领域。它是指构建和训练计算机系统，使之能够模仿人类的方式进行信息获取、信息分析、智能决策和自动学习，从而成为一个具备独立博弈能力的智能体。机器博弈不仅考验计算机系统的计算能力，更检验其在不确定环境下的推理、预测和决策水平。通过对竞争对手行为的模拟与反应，机器可以在复杂动态环境中通过学习和适应逐步优化自身策略，最终在博弈中取得最优结果。近年来，机器博弈在围棋、人机对弈、金融交易、市场竞争、自动驾驶等领域取得了显著进展。例如，AlphaGo 在围棋领域的成功标志着机器在高复杂度策略博弈中超越人类的里程碑。机器博弈的研究不仅推动了人工智能的发展，也为现实世界中的复杂竞争环境提供了重要的理论和技术支持。

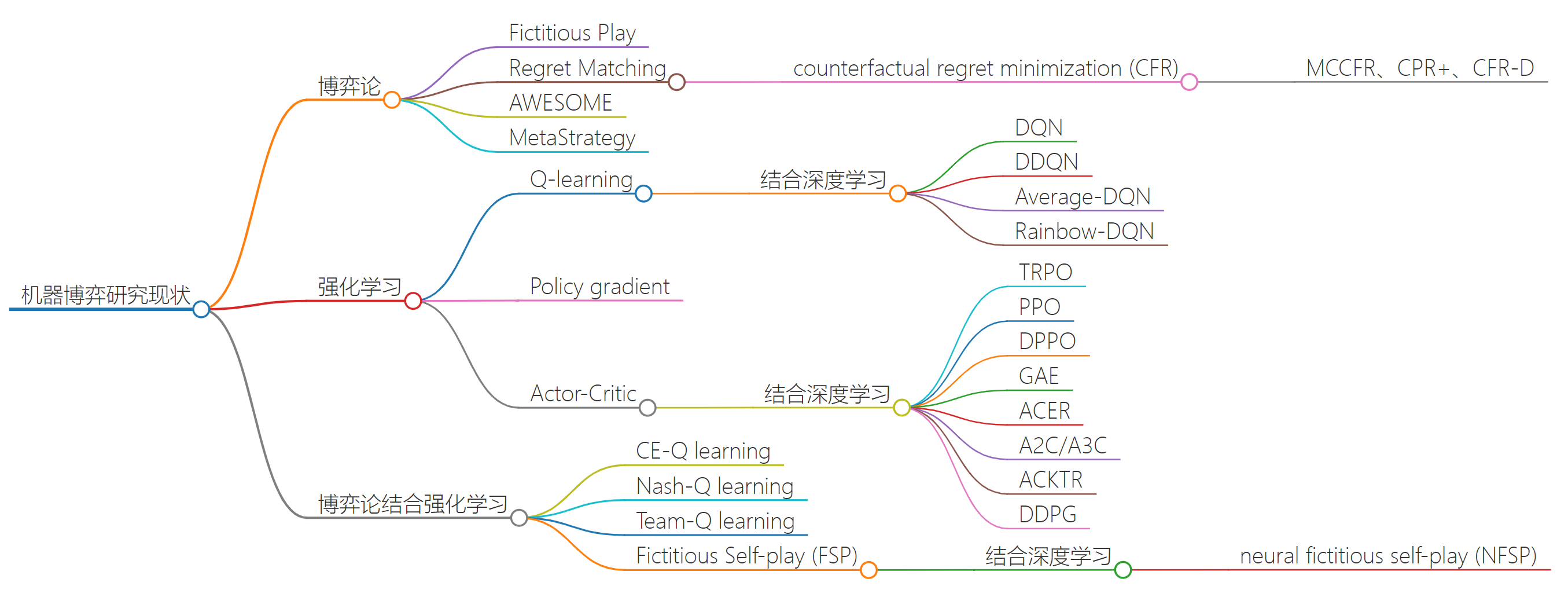
一、机器博弈概述

机器博弈（Machine Game）是人工智能（AI）与博弈论（Game Theory）相结合的产物，旨在通过构建和训练计算机系统，使其能够在不同的博弈环境下模仿人类的思维和行为，制定最优策略并在复杂环境中获得优势。机器博弈涉及算法设计、策略求解、规则设定等多个层面，已广泛应用于商业竞争、军事对抗、游戏竞技、市场博弈等多个领域。

1.1 机器博弈的基本框架

机器博弈的研究建立在博弈论和人工智能的理论基础之上。博弈论是研究理性个体在不同利益冲突和合作环境下如何做出最优决策的数学理论。博弈通常包括以下基本要素：

• 玩家（Player）：参与博弈的个体或智能体。
• 策略（Strategy）：玩家在博弈中可以采取的行动方案。
• 收益（Payoff）：玩家在博弈中根据自己的策略与其他玩家的策略组合所获得的结果。
• 信息集（Information Set）：玩家在做出决策时所拥有的信息集合。
• 均衡（Equilibrium）：在其他玩家策略保持不变的情况下，个体玩家采取最优策略所达到的状态。

人工智能（AI）通过机器学习、深度学习和强化学习等方法，能够在博弈环境中不断学习和优化策略，从而提高智能体在复杂博弈场景下的表现。机器博弈的基本框架包括两个主要的研究方向：

• 博弈策略的求解：通过算法（如最优策略、均衡求解、强化学习等）来获得不同博弈环境下的最优解。
• 博弈规则的设计：在对抗性环境下，设计博弈规则以引导个体理性行为，确保博弈结果的公平性和有效性。

1.2 机器博弈的理论基础

机器博弈（Machine Game Theory）是将博弈论（Game Theory）的理论框架与机器学习（Machine Learning）和人工智能（Artificial Intelligence）方法结合起来的交叉研究领域。博弈论为理解和建模多个智能体之间的竞争与合作行为提供了坚实的理论基础，而机器学习和人工智能则为求解博弈问题中的复杂均衡、动态调整和策略优化提供了强大的计算工具。在机器博弈中，核心目标是设计能够在博弈环境中自主学习、优化和决策的智能体，从而在复杂的对抗环境中获得最优策略或次优策略。在机器博弈中，智能体需要在动态变化的环境中通过博弈学习（Game Learning）方法，动态调整自己的策略，从而在复杂环境下获得最优或次优解。

纳什均衡与最优反应

在博弈论中，最优反应（Best Response, BR）指的是在给定其他玩家的策略下，使自身收益最大化的策略。假设一个有限博弈中存在\(n\) 个玩家，每个玩家的策略集合为\(S_i\)，收益函数为：

\[u_i(s_1, s_2, \ldots, s_n) \]

其中，\(s_i \in S_i\) 表示第\(i\) 个玩家的策略，\(s_{-i} = (s_1, \ldots, s_{i-1}, s_{i+1}, \ldots, s_n)\) 表示除第\(i\) 个玩家外其他玩家的策略组合。

玩家\(i\) 的最优反应集合\(B_i(s_{-i})\) 定义为在其他玩家策略给定的情况下，最大化自身收益的策略集合，即：

\[B_i(s_{-i}) = \arg\max_{s_i \in S_i} u_i(s_i, s_{-i}) \]

即，\(s_i\) 是玩家\(i\) 在给定其他玩家策略\(s_{-i}\) 下，最大化自身收益的最优选择。
纳什均衡（Nash Equilibrium）是博弈论中的核心概念，指在给定其他玩家策略不变的情况下，任一玩家选择自己的最优策略后，系统达到的稳定状态。即对于所有玩家\(i\in N\)，如果存在策略\(s_i^*\) 使得：

\[u_i(s_i^*, s_{-i}) \geq u_i(s_i', s_{-i}), \quad \forall s_i' \in S_i \]

则策略组合\((s_1^*, s_2^*, \ldots, s_N^*)\)为纳什均衡。

在机器博弈中，纳什均衡的求解是一个重要问题。由于在复杂的多智能体环境中，纳什均衡可能并不存在，或存在多个纳什均衡，因此机器博弈通常采用近似纳什均衡（Approximate Nash Equilibrium）或ε-纳什均衡作为最优解的替代。

遗憾最小化（Regret Minimization）

在机器博弈中，求解最优策略往往涉及到对遗憾（Regret）的最小化。对于某个玩家\(i\)，在第\(T\)轮博弈中，遗憾定义为：

\[R_i^T(s_i) = \sum_{t=1}^{T} \left[ u_i(s_i, s_{-i}^t) - u_i(s_i^t, s_{-i}^t) \right] \]

其中：

• \(s_i\)表示玩家\(i\)的最优策略
• \(s_i^t\)表示玩家\(i\)在第\(t\)轮所采用的策略
• \(s_{-i}^t\)表示其他玩家在第\(t\)轮的策略组合

在遗憾最小化框架下，机器博弈的目标是通过策略调整，使得长期平均遗憾趋近于零：

\[\bar{R}_i^T = \frac{1}{T} \sum_{t=1}^{T} R_i^t \to 0 \quad \text{当} \quad T \to \infty \]

常见的遗憾最小化算法包括：

• 增强学习（Reinforcement Learning, RL）
• 后悔匹配（Regret Matching）
• 在线学习（Online Learning）

在博弈学习过程中，智能体通过模拟和调整策略，逐步缩小遗憾值，从而逼近最优策略。

多智能体系统与协同学习

在机器博弈中，多智能体系统（Multi-Agent Systems, MAS）是核心研究对象。多智能体系统涉及多个自主智能体在共享环境中相互作用，这些智能体之间既可能存在竞争（Competitive）关系，也可能存在合作（Cooperative）关系。在竞争性环境中，每个智能体的目标是最大化自身收益，这通常导致纳什均衡的存在；而在合作性环境中，智能体的目标是最大化整体系统的效率，这需要设计全局优化策略。

常见的多智能体学习模型包括：

• 独立强化学习（Independent Q-Learning）：每个智能体独立学习，不考虑其他智能体的策略变化
• 联合强化学习（Joint Q-Learning）：智能体在学习过程中考虑其他智能体的策略
• 对抗性学习（Adversarial Learning）：在存在博弈竞争的环境中，智能体通过强化学习对抗其他智能体

演化博弈与策略优化

在复杂的动态环境中，机器博弈往往涉及演化博弈（Evolutionary Game Theory, EGT）过程。演化博弈通过模拟智能体在博弈环境中的不断演化和策略调整，寻找最优的长期生存和发展策略。常见的演化博弈方法包括：

• 遗传算法（Genetic Algorithm）
• 进化策略（Evolutionary Strategy）
• 基因规划（Genetic Programming）

在机器博弈中，演化博弈结合强化学习和遗憾最小化算法，可以在复杂的状态空间中高效求解最优策略。

1.3 机器博弈的应用场景

机器博弈在实际应用中涵盖了广泛的领域，主要包括以下几个方面：

游戏竞技

• 围棋：AlphaGo 使用深度强化学习和蒙特卡洛树搜索（MCTS）实现超越人类的围棋水平。
• 德州扑克：利用不完全信息博弈模型与遗憾最小化算法，Libratus 在德州扑克比赛中击败了顶级人类选手。
• 网络对战游戏：在《Dota 2》、《星际争霸》等多人游戏中，OpenAI Five 和 AlphaStar 展示了机器博弈在动态博弈环境中的卓越能力。

商业竞争

• 动态定价：在电商平台中，商家通过机器博弈模型在竞争中动态调整商品价格。
• 广告投放：Google 和 Facebook 通过博弈模型设计广告投放机制，以最大化广告主和平台收益。

金融与市场博弈

• 高频交易：交易系统通过博弈模型预测市场变化，优化交易策略。
• 风险对冲：通过动态博弈模型，投资者在不确定性环境下最大化投资收益。

军事与安全博弈

• 网络安全：通过机器博弈模型，模拟攻击与防御行为，设计最佳防御策略。
• 无人作战：利用博弈论求解无人机与导弹防御系统的最优策略。

多智能体协同

• 自动驾驶：通过多智能体博弈模型，模拟不同车辆在复杂路况下的动态博弈。
• 智能交通：通过博弈模型进行交通流量优化，减少拥堵和事故。

机器博弈的理论基础建立在传统博弈论的核心框架之上，通过引入强化学习、遗憾最小化、多智能体系统和演化博弈等方法，形成了动态博弈求解的新范式。纳什均衡和最优反应理论为机器博弈提供了求解的理论依据，遗憾最小化和演化博弈为动态策略调整和优化提供了有效的算法手段。通过在实际问题中灵活应用这些理论框架，机器博弈可以在围棋、德州扑克、网络对抗等复杂博弈环境中展现出强大的学习和适应能力。

二、ε-纳什均衡与平均遗憾值

纳什均衡（Nash Equilibrium）是博弈论中的核心概念，表示在一个博弈中，各个玩家在给定其他玩家策略的情况下都没有动机去改变自己的策略。换句话说，在纳什均衡下，每个玩家的策略都是对其他玩家策略的最优反应。

2.1 ε-纳什均衡

在严格的纳什均衡定义中，所有玩家都选择最优策略，使得没有玩家能够通过单方面改变策略来提高自己的收益。然而，在实际场景中，存在一定的误差或近似，因此引入ε-纳什均衡（ε-Nash Equilibrium）的概念。在一个\(n\)人非合作博弈中，若存在策略组合\((s_1^*, s_2^*, \ldots, s_n^*)\)，使得对于任意玩家\(i\)和任意可能的替代策略 \(s_i\)，满足以下条件：

\[u_i(s_i^*, s_{-i}^*) \geq u_i(s_i, s_{-i}^*) - \epsilon \]

其中：

• \(u_i(s_i^*, s_{-i}^*)\)为玩家\(i\)在策略组合\((s_i^*, s_{-i}^*)\)下的收益。
• $\epsilon \geq 0 $表示允许的最大收益损失。

当$\epsilon = 0 $时，回归为标准的纳什均衡。

2.2 平均遗憾值（Average Regret）

平均遗憾值是衡量策略优劣的重要指标，表示玩家在长期博弈中，由于未选择最优策略而损失的平均收益。
设\(t\) 为博弈的总轮数，\(s_i^t\) 为玩家$ i $ 在第$ t $ 轮选择的策略，\(s_{-i}^t\) 为其他玩家在第$ t $ 轮的策略。玩家$ i $ 在第$ t $ 轮的即时遗憾（Instantaneous Regret）定义为：

\[R_i^t = \max_{s_i} u_i(s_i, s_{-i}^t) - u_i(s_i^t, s_{-i}^t) \]

即玩家在第$ t $ 轮选择策略$ s_i^t $ 与最优策略的最大收益差值。

在\(t\) 轮博弈后，玩家的平均遗憾值（Average Regret）定义为：

\[\bar{R}_i(T) = \frac{1}{T} \sum_{t=1}^T R_i^t \]

如果随着\(t \to \infty\)，\(\bar{R}_i(T) \to 0\)，则称该策略为无悔策略（No-Regret Strategy）。

2.3 囚徒困境中的纳什均衡与平均遗憾值

在囚徒困境中，两个嫌疑犯 A 和 B 可以选择“沉默”或“坦白”。博弈的收益矩阵如下：

玩家 A / 玩家 B	坦白	沉默
坦白	-5, -5	0, -10
沉默	-10, 0	-1, -1

• 在纳什均衡下，双方都会选择“坦白”，即策略组合为 ( (坦白, 坦白) )，此时收益为 ( (-5, -5) )。
• 如果 A 尝试改变策略，选择“沉默”，但 B 保持“坦白”，A 的收益将为 ( -10 )，更低于 ( -5 )，因此 A 没有动力去改变策略。
• 平均遗憾值在多轮博弈中通过调整策略逐渐降低，趋于纳什均衡。

2.4 石头-剪刀-布（RPS）中的纳什均衡与平均遗憾值

在石头-剪刀-布博弈中，收益矩阵为：

玩家 A \ 玩家 B	石头	剪刀	布
石头	0, 0	1, -1	-1, 1
剪刀	-1, 1	0, 0	1, -1
布	1, -1	-1, 1	0, 0

• 在纯策略下，不存在纳什均衡。
• 在混合策略下，唯一的纳什均衡是双方都以\(\frac{1}{3}\)的概率选择“石头”、“剪刀”和“布”。
• 在长期博弈中，通过最优反应策略和遗憾最小化方法，双方的平均遗憾值逐渐降低，趋于均衡。

通过最优反应和遗憾最小化策略，玩家可以在多轮博弈中调整策略，最终趋近于纳什均衡或\(\epsilon\)-纳什均衡。

三、古诺博弈的机器博弈

古诺博弈（Cournot Game）是最早提出的寡头市场博弈模型之一，描述了两个或多个企业在市场中通过调整产量来竞争，从而决定市场价格和收益。古诺博弈的关键假设是：

• 每个企业独立决定自己的产量。
• 市场价格取决于总供给量。
• 企业的目标是通过调整产量来最大化自身收益。

3.1 古诺博弈的基本模型

假设在一个市场中存在两个厂商（玩家），它们的产量分别为 $ q_1 $ 和 $ q_2 $，市场价格 $ P(Q) $ 由总产量 $ Q = q_1 + q_2 $ 决定，假设市场价格函数为：

\[P(Q) = a - bQ \]

其中：

• $ a > 0 $ 表示市场初始价格水平。
• $ b > 0 $ 表示市场需求对供给的敏感度。

每个厂商的成本函数为：

\[C_i(q_i) = c q_i \]

其中 $ c $ 为单位成本。厂商 $ i $ 的利润为：

\[\pi_i(q_1, q_2) = q_i \cdot (P(Q) - c) = q_i \cdot (a - b(q_1 + q_2) - c) \]

3.2 最优反应函数的推导

每个厂商的目标是最大化自身的利润：

\[\max_{q_i} \pi_i(q_1, q_2) = q_i \cdot (a - b(q_1 + q_2) - c) \]

对 $ q_i $ 求导，得：

\[\frac{\partial \pi_i}{\partial q_i} = a - bq_1 - bq_2 - c - bq_i \]

令 $ \frac{\partial \pi_i}{\partial q_i} = 0 $，解得：

\[q_i^* = \frac{a - c - bq_{-i}}{2b} \]

这是厂商 $ i $ 的最优反应函数。

对于两个厂商，最优反应函数分别为：

\[q_1^* = \frac{a - c - bq_2}{2b}, \quad q_2^* = \frac{a - c - bq_1}{2b} \]

解联立方程组，得均衡解：

\[q_1^* = q_2^* = \frac{a - c}{3b} \]

在均衡状态下，总产量为：

\[Q^* = q_1^* + q_2^* = \frac{2(a - c)}{3b} \]

市场价格为：

\[P^* = a - bQ^* = a - b \cdot \frac{2(a - c)}{3b} = \frac{a + 2c}{3} \]

每个厂商的均衡利润为：

\[\pi_i^* = q_i^* \cdot (P^* - c) = \frac{(a - c)^2}{9b} \]

3.3 机器博弈过程

在机器博弈中，两个厂商根据最优反应函数不断调整产量，经过多轮博弈，逐渐收敛于纳什均衡。

• 初始产量随机设置。
• 根据对方产量，利用最优反应函数调整产量。
• 经过多轮调整，产量和价格趋于稳定。
• 平均遗憾值逐渐减小，最终收敛于纳什均衡。

3.4 Python程序

import numpy as np
import matplotlib.pyplot as plt

# 参数设置
a = 100      # 市场初始价格
b = 2        # 市场需求敏感度
c = 20       # 单位成本
iterations = 30  # 最大迭代次数

# 初始产量（随机设置）
q1 = np.random.uniform(0, 20)
q2 = np.random.uniform(0, 20)

# 用于存储每轮产量和利润
q1_history = [q1]
q2_history = [q2]
profit1_history = []
profit2_history = []

# 机器博弈过程
for i in range(iterations):
    # 依据最优反应函数更新产量
    q1 = (a - c - b * q2) / (2 * b)
    q2 = (a - c - b * q1) / (2 * b)

    # 记录产量和利润
    q1_history.append(q1)
    q2_history.append(q2)
    profit1 = q1 * (a - b * (q1 + q2) - c)
    profit2 = q2 * (a - b * (q1 + q2) - c)
    profit1_history.append(profit1)
    profit2_history.append(profit2)

# 画出产量和利润的变化
plt.figure(figsize=(14, 6))

# 产量调整过程
plt.subplot(1, 2, 1)
plt.plot(q1_history, label="Firm 1 Output", linewidth=3)  # 加粗
plt.plot(q2_history, label="Firm 2 Output", linewidth=3)  # 加粗
plt.axhline((a - c) / (3 * b), color='red', linestyle='--', label='Nash Equilibrium Output', linewidth=2)  # 加粗
plt.title("Output Adjustment Process")
plt.xlabel("Iteration")
plt.ylabel("Output")
plt.legend()

# 利润调整过程
plt.subplot(1, 2, 2)
plt.plot(profit1_history, label="Firm 1 Profit", linewidth=2)  # 加粗
plt.plot(profit2_history, label="Firm 2 Profit", linewidth=2)  # 加粗
plt.axhline(((a - c) ** 2) / (9 * b), color='red', linestyle='--', label='Nash Equilibrium Profit', linewidth=2)  # 加粗
plt.title("Profit Adjustment Process")
plt.xlabel("Iteration")
plt.ylabel("Profit")
plt.legend()

# 布局调整
plt.tight_layout()
plt.show()

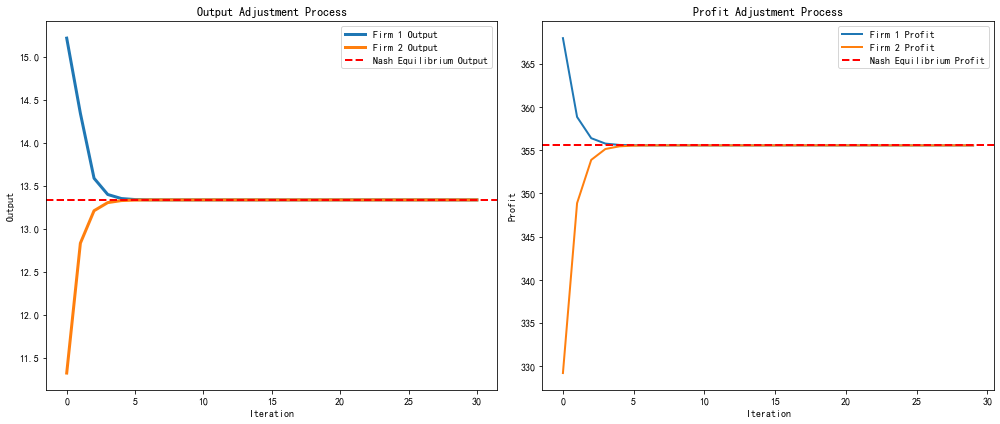
3.5 结果分析

• 在初始状态下，两个厂商的产量和利润波动较大。
• 经过多轮机器博弈后，两个厂商的产量和利润逐渐趋于稳定。
• 最终产量和利润收敛于纳什均衡值：
  • 均衡产量：\(q_1^* = q_2^* = \frac{a - c}{3b}\)
  • 均衡利润：\(\pi_i^* = \frac{(a - c)^2}{9b}\)

总结

机器博弈作为人工智能与博弈论结合的前沿领域，已在游戏、金融、商业和军事等领域展现出巨大潜力。其理论基础建立在纳什均衡、最优反应和遗憾最小化等经典博弈论框架之上，结合强化学习、多智能体系统和演化博弈等方法，使智能体在复杂环境中实现自主学习和策略优化。纳什均衡为机器博弈的求解提供了理论依据，遗憾最小化方法通过动态调整策略使长期平均损失最小化，强化学习和演化博弈使智能体能够在动态环境中不断进化和适应。
器博弈的发展将呈现以下趋势：首先，深度学习与博弈求解结合，将强化学习与深度神经网络相结合，提升求解复杂博弈问题的能力；其次，大规模博弈建模与优化将通过并行计算和分布式系统提高求解效率；第三，动态博弈的复杂均衡求解将在不完全信息环境下探索新的均衡方法；最后，隐私保护与公平博弈将推动在多智能体环境中设计公平和安全的博弈机制。通过深入研究这些理论和方法，机器博弈将在智能决策和复杂博弈问题求解中发挥更大作用。

参考文献

1. 机器博弈研究现状
2. 机器博弈 (二) 遗憾最小化算法