计量经济学(八)——格兰杰(Granger causality)因果模型
格兰杰因果模型(Granger Causality Model)是时间序列分析中的一种重要工具,用于检测两个变量之间的动态因果关系。该模型由经济学家克莱夫·格兰杰于1969年提出,旨在确定一个时间序列变量能否通过其过去的信息来有效预测另一个变量的变化。格兰杰因果模型并不代表实际的因果关系,而是通过比较不同回归模型中残差的大小,判断某一变量的历史值是否显著提升了另一变量的预测精度。具体来说,如果引入某一变量的过去值能显著提高对目标变量的预测效果,则认为该变量格兰杰导致了目标变量。
格兰杰因果检验在经济学、金融学等领域广泛应用,尤其在分析股票市场、货币政策和宏观经济变量间的相互作用时提供了理论依据。它为研究者提供了一种有效的工具来识别时间序列之间的潜在因果联系,并为经济决策和金融风险管理提供了重要的参考。然而,格兰杰因果模型只适用于平稳的时间序列,且“因果性”仅指预测能力,实际的因果关系仍需其他工具来验证。
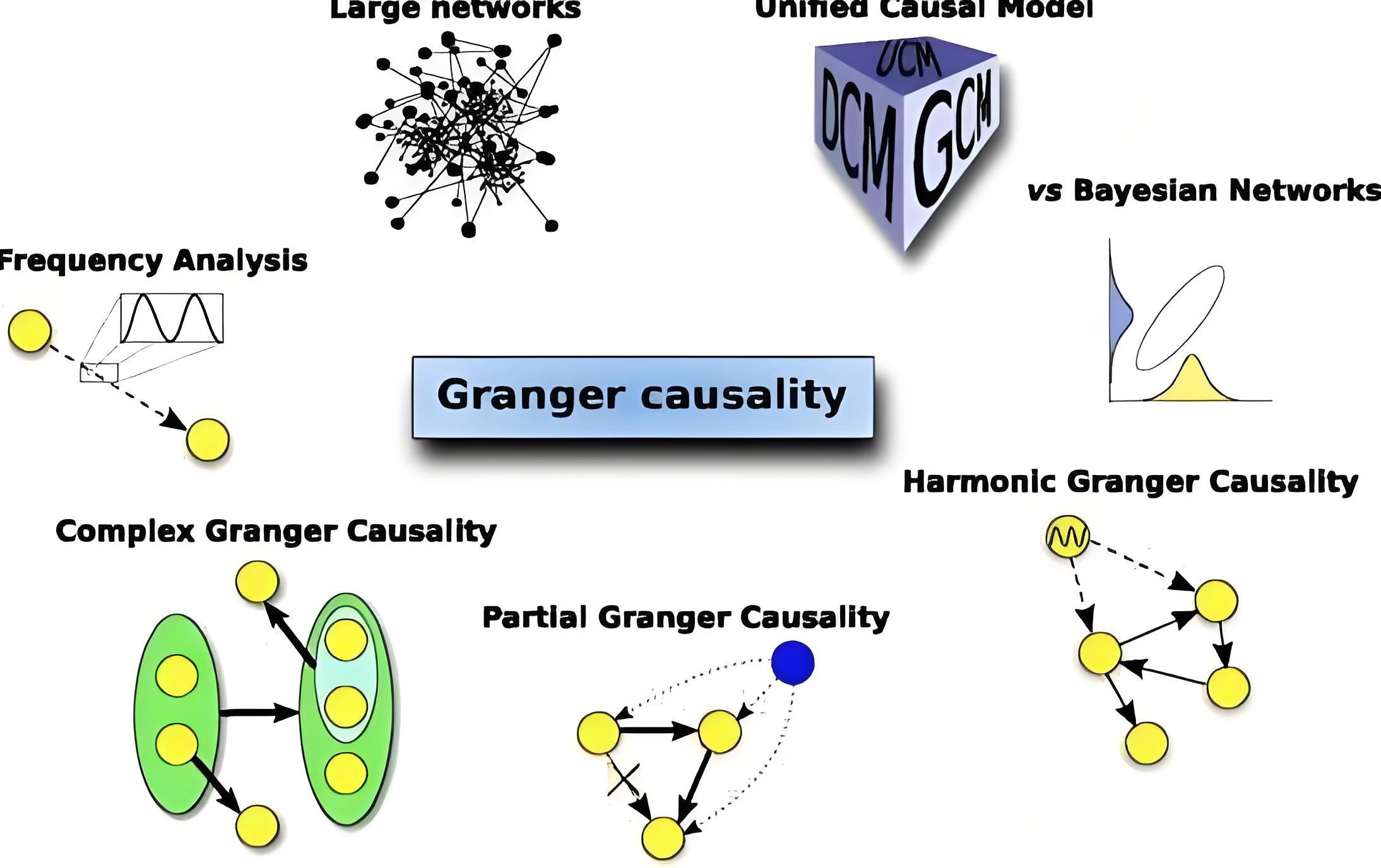
零、因果关系检验方法
0.1 Granger 因果检验(Granger Causality Test)
Granger 因果检验是时间序列分析中应用最广泛的一种方法。它最早由经济学家克莱夫·格兰杰提出,用于确定一个时间序列是否能够帮助预测另一个时间序列。Granger 因果检验的基础假设是,因果关系体现在时间上的先后顺序上。如果一个变量 X 的历史数据能显著地帮助预测另一个变量 Y,而 Y 的历史数据不能显著改善对 X 的预测,则可以认为 X “Granger 导致” Y。
使用场景:Granger 因果检验在经济学、金融市场和气候研究等领域广泛应用。例如,研究股票价格是否可以预测宏观经济指标的变化,或者气候变化因素是否可以解释某些生态系统的变化。在这些场景中,Granger 因果检验能够帮助分析时间序列之间的相互依赖关系。
限制:Granger 因果检验的有效性依赖于一些严格的假设。首先,变量之间必须是平稳的时间序列,非平稳数据会影响检验结果的准确性。其次,Granger 因果检验捕捉的是统计上的关联性,而不是真正的因果关系。例如,在存在第三方隐藏变量的情况下,Granger 因果检验可能会给出误导性的因果判断。因此,研究者常常结合其他因果检测方法来进一步验证结果。
0.2 结构方程模型(SEM)
结构方程模型(Structural Equation Modeling,SEM)是一种多变量统计分析方法,广泛用于探讨变量之间的因果关系。与Granger 因果检验不同,SEM不仅关注显性变量的因果关系,还可以分析潜在变量(即不可直接观测的变量)之间的因果链条。
使用场景:SEM 常用于社会科学研究中,例如心理学、教育学等领域,研究者通过 SEM 分析个体行为、态度、能力等潜在变量对观测数据的影响。同时,SEM 在市场营销、战略管理、组织行为等领域也被广泛应用,用以分析复杂变量体系下的因果链条。
限制:SEM 需要明确的理论假设支持,模型的建构过程依赖于研究者对数据的深入理解。如果假设的模型结构不符合实际,可能会导致错误的结论。此外,SEM 通常适用于大样本数据,样本量过小可能会导致估计结果不稳定。
0.3 贝叶斯网络(Bayesian Networks)
贝叶斯网络是一种基于概率论的因果模型,它利用有向无环图(Directed Acyclic Graph, DAG)来表示变量之间的条件独立性与因果关系。贝叶斯网络结合了概率论和图论,能够在存在多个潜在变量时推导出复杂的因果结构。
使用场景:贝叶斯网络广泛应用于机器学习、医学诊断和人工智能领域。例如,在医学诊断中,贝叶斯网络可以用于推断症状之间的因果关系,帮助医生确定疾病的最可能成因。在金融领域,贝叶斯网络可以用于风险评估和预测市场变化,识别潜在的因果驱动因素。
限制:尽管贝叶斯网络强大且灵活,但它也有一些限制。首先,贝叶斯网络的因果推理结果依赖于观测到的数据和假设的图结构,因此在数据稀疏或存在潜在混杂变量时,推断结果可能不准确。其次,构建贝叶斯网络需要大量的计算资源,尤其在高维数据场景下计算复杂度较高。
0.4 双向频谱分析(Bivariate Spectral Analysis)
双向频谱分析是基于频域的因果检测方法,特别适用于处理周期性或振荡性数据。通过分析两个变量之间的交叉谱,双向频谱分析可以识别特定频率下一个信号是否能够预测另一个信号的行为。
使用场景:双向频谱分析主要用于气象学、神经科学等领域。例如,在大气科学中,双向频谱分析被用来研究气象变量(如气温和气压)之间的周期性依赖关系。在神经科学研究中,它用于分析脑电波的同步性和因果互动。
限制:双向频谱分析的局限在于它只能识别频域中的相关性,而不是因果关系的方向性。此外,对于非周期性或非平稳的时间序列,双向频谱分析的效果可能不如基于时域的因果检验方法。

以上介绍的几种因果检测方法各具特点,适用于不同类型的数据和研究背景。Granger 因果检验作为最经典的时间序列因果分析方法,适用于捕捉时间顺序上的因果关系。而结构方程模型、贝叶斯网络等方法则更侧重于复杂变量间的因果结构解析。研究者可以根据数据的特性、分析目标以及领域背景,选择最合适的因果检测方法。
一、格兰杰因果检验原理
格兰杰因果检验是一种用于确定时间序列变量之间因果关系的统计方法。它基于时间序列的预测能力,而非严格的因果关系。该方法由诺贝尔经济学奖得主克莱夫·格兰杰提出,广泛应用于金融市场、宏观经济等领域。
如果在给定\(Y\)的历史数据基础上,加入\(X\)的历史数据能够显著提高对\(Y\)的预测能力,则称\(X\)格兰杰导致\(Y\)。格兰杰因果性关注的是一个变量过去的信息对另一个变量的预测能力。
1.1 格兰杰因果检验的数学表达
给定两个平稳时间序列\(X_t\)和\(Y_t\),通过对比以下两种回归模型来判断它们之间是否存在因果关系:
- 单变量自回归模型:\[Y_t = \alpha_0 + \alpha_1 Y_{t-1} + \alpha_2 Y_{t-2} + \cdots + \alpha_p Y_{t-p} + \epsilon_t \]
- 多变量回归模型:\[Y_t = \beta_0 + \beta_1 Y_{t-1} + \beta_2 Y_{t-2} + \cdots + \beta_p Y_{t-p} + \gamma_1 X_{t-1} + \gamma_2 X_{t-2} + \cdots + \gamma_q X_{t-q} + \eta_t \]
如多变量回归模型(\(p=3; q=4\))
当 \(t=10\) 时:
选择合适的滞后阶数\(p\)和\(q\),通常通过信息准则(如AIC、BIC)来决定。
1.2 格兰杰因果检验步骤
- 平稳性检验。进行因果检验前,先对数据进行平稳性检验,如ADF检验或KPSS检验。如果数据不平稳,可以通过差分变换使其平稳。
- 模型建立。根据两个时间序列的数据,建立AR模型和包含多个滞后项的回归模型。具体步骤包括:
单变量自回归模型:仅使用一个变量的过去值进行回归分析。
多变量回归模型:加入另一个变量的过去值,进行联合回归分析。 - F检验
格兰杰因果检验的核心在于对两个模型进行比较。通过F检验来判断引入\(X_t\)的过去值是否能够显著提高对\(Y_t\)的预测能力。F检验的原假设是“\(X_t\)不格兰杰导致\(Y_t\)”,备择假设是“\(X_t\)格兰杰导致\(Y_t\)”。F检验的公式为:$$F = \frac{(RSS_r - RSS_{ur}) / q}{RSS_{ur} / (n - k)} $$ 其中:- \(RSS_r\)是单变量自回归模型的残差平方和。
- \(RSS_{ur}\)是多变量回归模型的残差平方和。
- \(q\)是引入的滞后项个数。
- \(n\)是样本量。
- \(k\)是模型中的解释变量个数。
如果F统计量大于临界值,或者p值小于显著性水平,则拒绝原假设,说明\(X_t\)格兰杰导致\(Y_t\)。
- 双向检验
格兰杰因果检验通常是双向的。除了检验\(X_t\)是否格兰杰导致\(Y_t\),还需要检验\(Y_t\)是否格兰杰导致\(X_t\)。通过双向检验,可以更全面地理解两个变量之间的动态关系。
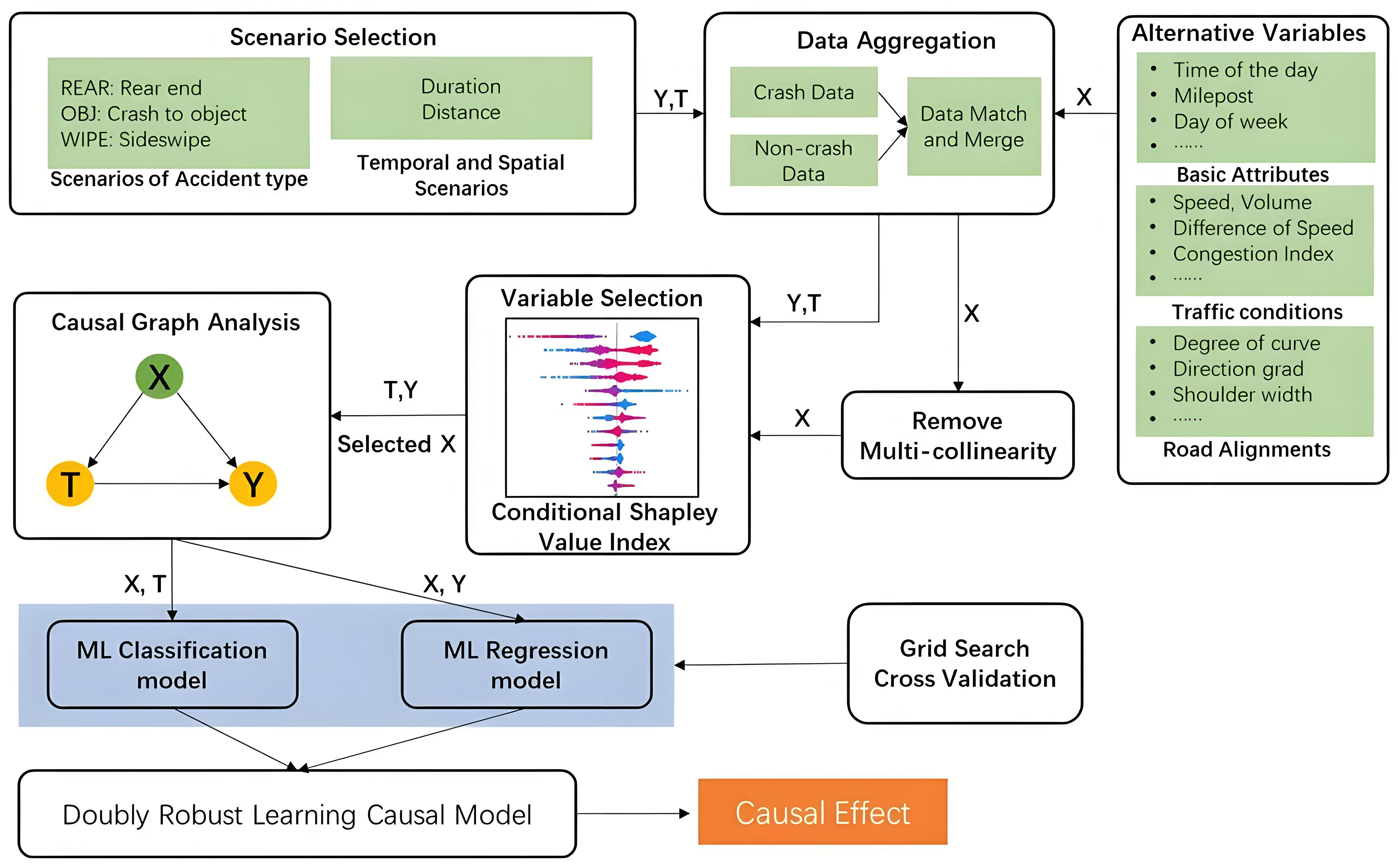
二、案例分析
检验1981~2013年我国居民实际消费总支出年增长率 (GY) 和实际可支配收入年增长率 (GX) 时间序列之间的因果关系。该研究旨在分析1981年至2013年间,我国居民的实际消费总支出年增长率 (GY) 与实际可支配收入年增长率 (GX) 之间的统计关联和潜在因果效应。通过分析这两个经济指标的时间序列数据,可以揭示它们之间的动态关系,为理解消费行为和制定相关经济政策提供依据。
| 年份 | GY | GX | 年份 | GY | GX | 年份 | GY | GX |
|---|---|---|---|---|---|---|---|---|
| 1981 | 0.099473 | 0.062099 | 1982 | 0.082741 | 0.094567 | 1983 | 0.091417 | 0.090969 |
| 1984 | 0.127428 | 0.147912 | 1985 | 0.145660 | 0.003061 | 1986 | 0.062468 | 0.123817 |
| 1987 | 0.076548 | 0.122000 | 1988 | 0.081482 | 0.079701 | 1989 | -0.049696 | -0.048035 |
| 1990 | 0.040257 | 0.099168 | 1991 | 0.097858 | 0.146047 | 1992 | 0.138718 | 0.164554 |
| 1993 | 0.100700 | 0.174172 | 1994 | 0.072262 | 0.111463 | 1995 | 0.109241 | 0.083073 |
| 1996 | 0.105028 | 0.085910 | 1997 | 0.057785 | 0.062081 | 1998 | 0.071002 | 0.060773 |
| 1999 | 0.083955 | 0.056033 | 2000 | 0.089322 | 0.066737 | 2001 | 0.070681 | 0.080250 |
| 2002 | 0.081920 | 0.106086 | 2003 | 0.073655 | 0.120293 | 2004 | 0.088857 | 0.129201 |
| 2005 | 0.098908 | 0.139262 | 2006 | 0.115015 | 0.166874 | 2007 | 0.113153 | 0.122116 |
| 2008 | 0.094716 | 0.157067 | 2009 | 0.114582 | 0.075955 | 2010 | 0.102600 | 0.103122 |
| 2011 | 0.138954 | 0.102237 | 2012 | 0.066299 | 0.058626 | 2013 | 0.118778 | 0.115859 |
2.1 GY和GX的时序图
import pandas as pd
import matplotlib.pyplot as plt
from matplotlib import font_manager
# 设置中文字体,避免中文乱码
plt.rcParams['font.sans-serif'] = ['SimHei'] # 使用黑体字(SimHei)
plt.rcParams['axes.unicode_minus'] = False # 解决负号显示问题
# 创建数据表
data = {
'年份': [1981, 1982, 1983, 1984, 1985, 1986, 1987, 1988, 1989, 1990, 1991, 1992, 1993, 1994, 1995, 1996, 1997, 1998, 1999, 2000, 2001, 2002, 2003, 2004, 2005, 2006, 2007, 2008, 2009, 2010, 2011, 2012, 2013],
'GY': [0.099473, 0.082741, 0.091417, 0.127428, 0.145660, 0.062468, 0.076548, 0.081482, -0.049696, 0.040257, 0.097858, 0.138718, 0.100700, 0.072262, 0.109241, 0.105028, 0.057785, 0.071002, 0.083955, 0.089322, 0.070681, 0.081920, 0.073655, 0.088857, 0.098908, 0.115015, 0.113153, 0.094716, 0.114582, 0.102600, 0.138954, 0.066299, 0.118778],
'GX': [0.062099, 0.094567, 0.090969, 0.147912, 0.003061, 0.123817, 0.122000, 0.079701, -0.048035, 0.099168, 0.146047, 0.164554, 0.174172, 0.111463, 0.083073, 0.085910, 0.062081, 0.060773, 0.056033, 0.066737, 0.080250, 0.106086, 0.120293, 0.129201, 0.139262, 0.166874, 0.122116, 0.157067, 0.075955, 0.103122, 0.102237, 0.058626, 0.115859]
}
# 转换为 pandas DataFrame
df = pd.DataFrame(data)
# 创建图形
plt.figure(figsize=(10, 6))
# 绘制 GY 曲线
plt.plot(df['年份'], df['GY'], label='GY', marker='o')
# 绘制 GX 曲线
plt.plot(df['年份'], df['GX'], label='GX', marker='s')
# 添加标题和标签
plt.title('GY 和 GX 随年份的变化', fontsize=14)
plt.xlabel('年份', fontsize=12)
plt.ylabel('值', fontsize=12)
# 显示图例
plt.legend()
# 添加网格线
plt.grid(True)
# 显示图形
plt.show()

2.2 格兰杰因果检验程序
import pandas as pd
import statsmodels.api as sm
from statsmodels.tsa.stattools import adfuller, grangercausalitytests
# -----------------------------
# 数据准备
# -----------------------------
data = {
'年份': list(range(1981, 2014)),
'GY': [0.099473, 0.082741, 0.091417, 0.127428, 0.145660, 0.062468, 0.076548, 0.081482,
-0.049696, 0.040257, 0.097858, 0.138718, 0.100700, 0.072262, 0.109241, 0.105028,
0.057785, 0.071002, 0.083955, 0.089322, 0.070681, 0.081920, 0.073655, 0.088857,
0.098908, 0.115015, 0.113153, 0.094716, 0.114582, 0.102600, 0.138954, 0.066299, 0.118778],
'GX': [0.062099, 0.094567, 0.090969, 0.147912, 0.003061, 0.123817, 0.122000, 0.079701,
-0.048035, 0.099168, 0.146047, 0.164554, 0.174172, 0.111463, 0.083073, 0.085910,
0.062081, 0.060773, 0.056033, 0.066737, 0.080250, 0.106086, 0.120293, 0.129201,
0.139262, 0.166874, 0.122116, 0.157067, 0.075955, 0.103122, 0.102237, 0.058626, 0.115859]
}
df = pd.DataFrame(data)
# -----------------------------
# ADF 检验函数
# -----------------------------
def adf_test(series):
res = adfuller(series)
return {
'ADF Statistic': round(res[0], 2),
'p-value': round(res[1], 2),
'Critical Values': {k: round(v, 2) for k, v in res[4].items()}
}
# 原序列 ADF
print("GY的ADF检验结果:", adf_test(df['GY']))
print("GX的ADF检验结果:", adf_test(df['GX']))
# 差分序列
df_diff = df[['GY','GX']].diff().dropna()
print("GY差分后的ADF检验结果:", adf_test(df_diff['GY']))
print("GX差分后的ADF检验结果:", adf_test(df_diff['GX']))
# -----------------------------
# 格兰杰因果检验
# -----------------------------
max_lag = 5
print("\n格兰杰因果检验结果(GX -> GY):")
grangercausalitytests(df[['GY','GX']], maxlag=max_lag, verbose=True)
print("\n格兰杰因果检验结果(GY -> GX):")
grangercausalitytests(df[['GX','GY']], maxlag=max_lag, verbose=True)
# -----------------------------
# VAR 模型拟合
# -----------------------------
model = sm.tsa.VAR(df_diff)
var_result = model.fit(max_lag)
# 输出系数矩阵
print("\nVAR模型系数矩阵:")
print(var_result.params)
# 自动生成 LaTeX 表达式
GY_eq = f"GY_t = {var_result.params.loc['const','GY']:.4f}"
GX_eq = f"GX_t = {var_result.params.loc['const','GX']:.4f}"
for lag in range(1, var_result.k_ar+1):
GY_eq += f" + {var_result.params.loc[f'L{lag}.GY','GY']:.4f} GY_{{t-{lag}}} + {var_result.params.loc[f'L{lag}.GX','GY']:.4f} GX_{{t-{lag}}}"
GX_eq += f" + {var_result.params.loc[f'L{lag}.GX','GX']:.4f} GX_{{t-{lag}}} + {var_result.params.loc[f'L{lag}.GY','GX']:.4f} GY_{{t-{lag}}}"
GY_eq += " + \\varepsilon_{GY,t}"
GX_eq += " + \\varepsilon_{GX,t}"
latex_model = "\\begin{cases}\n" + GY_eq + " \\\\\n" + GX_eq + "\n\\end{cases}"
print("\nLaTeX格式VAR模型表达:")
print(latex_model)
2.3 结果输出
GY的ADF检验结果: {'ADF Statistic': -4.14, 'p-value': 0.0, 'Critical Values': {'1%': -3.65, '5%': -2.96, '10%': -2.62}}
GX的ADF检验结果: {'ADF Statistic': -2.4, 'p-value': 0.14, 'Critical Values': {'1%': -3.71, '5%': -2.98, '10%': -2.63}}
GY差分后的ADF检验结果: {'ADF Statistic': -3.22, 'p-value': 0.02, 'Critical Values': {'1%': -3.72, '5%': -2.99, '10%': -2.63}}
GX差分后的ADF检验结果: {'ADF Statistic': -3.23, 'p-value': 0.02, 'Critical Values': {'1%': -3.69, '5%': -2.97, '10%': -2.63}}
格兰杰因果检验结果(GX -> GY):
Granger Causality
number of lags (no zero) 1
ssr based F test: F=3.8560 , p=0.0592 , df_denom=29, df_num=1
ssr based chi2 test: chi2=4.2549 , p=0.0391 , df=1
likelihood ratio test: chi2=3.9949 , p=0.0456 , df=1
parameter F test: F=3.8560 , p=0.0592 , df_denom=29, df_num=1
Granger Causality
number of lags (no zero) 2
ssr based F test: F=1.7404 , p=0.1953 , df_denom=26, df_num=2
ssr based chi2 test: chi2=4.1502 , p=0.1255 , df=2
likelihood ratio test: chi2=3.8949 , p=0.1426 , df=2
parameter F test: F=1.7404 , p=0.1953 , df_denom=26, df_num=2
Granger Causality
number of lags (no zero) 3
ssr based F test: F=1.0590 , p=0.3857 , df_denom=23, df_num=3
ssr based chi2 test: chi2=4.1438 , p=0.2463 , df=3
likelihood ratio test: chi2=3.8815 , p=0.2745 , df=3
parameter F test: F=1.0590 , p=0.3857 , df_denom=23, df_num=3
Granger Causality
number of lags (no zero) 4
ssr based F test: F=1.7704 , p=0.1744 , df_denom=20, df_num=4
ssr based chi2 test: chi2=10.2683 , p=0.0361 , df=4
likelihood ratio test: chi2=8.7905 , p=0.0666 , df=4
parameter F test: F=1.7704 , p=0.1744 , df_denom=20, df_num=4
Granger Causality
number of lags (no zero) 5
ssr based F test: F=1.7177 , p=0.1844 , df_denom=17, df_num=5
ssr based chi2 test: chi2=14.1457 , p=0.0147 , df=5
likelihood ratio test: chi2=11.4500 , p=0.0432 , df=5
parameter F test: F=1.7177 , p=0.1844 , df_denom=17, df_num=5
格兰杰因果检验结果(GY -> GX):
Granger Causality
number of lags (no zero) 1
ssr based F test: F=0.2315 , p=0.6340 , df_denom=29, df_num=1
ssr based chi2 test: chi2=0.2555 , p=0.6132 , df=1
likelihood ratio test: chi2=0.2545 , p=0.6139 , df=1
parameter F test: F=0.2315 , p=0.6340 , df_denom=29, df_num=1
Granger Causality
number of lags (no zero) 2
ssr based F test: F=0.2117 , p=0.8106 , df_denom=26, df_num=2
ssr based chi2 test: chi2=0.5048 , p=0.7769 , df=2
likelihood ratio test: chi2=0.5007 , p=0.7785 , df=2
parameter F test: F=0.2117 , p=0.8106 , df_denom=26, df_num=2
Granger Causality
number of lags (no zero) 3
ssr based F test: F=0.3428 , p=0.7946 , df_denom=23, df_num=3
ssr based chi2 test: chi2=1.3414 , p=0.7193 , df=3
likelihood ratio test: chi2=1.3122 , p=0.7262 , df=3
parameter F test: F=0.3428 , p=0.7946 , df_denom=23, df_num=3
Granger Causality
number of lags (no zero) 4
ssr based F test: F=3.0108 , p=0.0427 , df_denom=20, df_num=4
ssr based chi2 test: chi2=17.4625 , p=0.0016 , df=4
likelihood ratio test: chi2=13.6691 , p=0.0084 , df=4
parameter F test: F=3.0108 , p=0.0427 , df_denom=20, df_num=4
Granger Causality
number of lags (no zero) 5
ssr based F test: F=1.4760 , p=0.2491 , df_denom=17, df_num=5
ssr based chi2 test: chi2=12.1554 , p=0.0327 , df=5
likelihood ratio test: chi2=10.0955 , p=0.0726 , df=5
parameter F test: F=1.4760 , p=0.2491 , df_denom=17, df_num=5
LaTeX格式VAR模型表达:
\begin{cases}
GY_t = 0.0001 + -0.5956 GY_{t-1} + 0.1949 GX_{t-1} + -0.2813 GY_{t-2} + 0.1091 GX_{t-2} + -0.3087 GY_{t-3} + -0.0617 GX_{t-3} + -0.3986 GY_{t-4} + 0.2800 GX_{t-4} + -0.2037 GY_{t-5} + 0.2595 GX_{t-5} + \varepsilon_{GY,t} \\
GX_t = -0.0001 + -0.2772 GX_{t-1} + -0.2733 GY_{t-1} + -0.0688 GX_{t-2} + -0.1649 GY_{t-2} + -0.0747 GX_{t-3} + -0.4607 GY_{t-3} + 0.3285 GX_{t-4} + -0.9283 GY_{t-4} + 0.2858 GX_{t-5} + -0.5938 GY_{t-5} + \varepsilon_{GX,t}
基于AIC选择的滞后阶数\((p=5)\):
总结
格兰杰因果检验(Granger Causality Test)是一种强有力的工具,广泛应用于时间序列数据的因果关系分析。它通过检验一个时间序列变量的过去值是否能够显著提高对另一个变量未来值的预测,来判断两者之间是否存在因果关系。具体而言,格兰杰因果检验通过构建两个回归模型:一个仅使用被解释变量的滞后项,另一个加入解释变量的滞后项。随后,研究者通过F检验对这两个模型的优劣进行比较。如果加入解释变量的滞后项显著提高了预测效果,则可以认为该变量“格兰杰导致”了另一个变量的变化。
然而,格兰杰因果检验仅是一种统计上的工具,因其基于预测能力而非实际的因果机制,因此在解释结果时需要谨慎。特别是在处理复杂的经济和金融数据时,研究者应结合其他分析方法,例如协整检验、脉冲响应分析等,以避免误判因果关系。此外,该方法仅适用于平稳的时间序列,因此在使用前需要对数据进行平稳性检验。总之,格兰杰因果检验提供了识别时间序列间动态关系的重要手段,但在实际应用中,需结合多种分析工具,以确保结果的可靠性和有效性。




 浙公网安备 33010602011771号
浙公网安备 33010602011771号