KNN算法思想与Python实现
KNN(k- Nearest Neighbor,简称为KNN)法即k最邻近法,最初由 Cover和Hart于1968年提出,是一个理论上比较成熟的方法,也是最简单的机器学习算法之一,它的适用面很广,并且在样本量足够大的情况下准确度很高,多年来得到了很多的关注和研究。k最近邻(KNN)算法是一种简单而有效的监督学习算法,用于分类和回归问题。该算法的核心思想是根据新样本与已有样本之间的相似度,来预测新样本的标签或值。一提到KNN,很多人都想起了另外一个比较经典的聚类算法K-means,但其实,二者之间是有很多不同的,这两种算法之间的根本区别是,K-means本质上是无监督学习而KNN是监督学习,Kmeans是聚类算法而KNN是分类(或回归)算法。
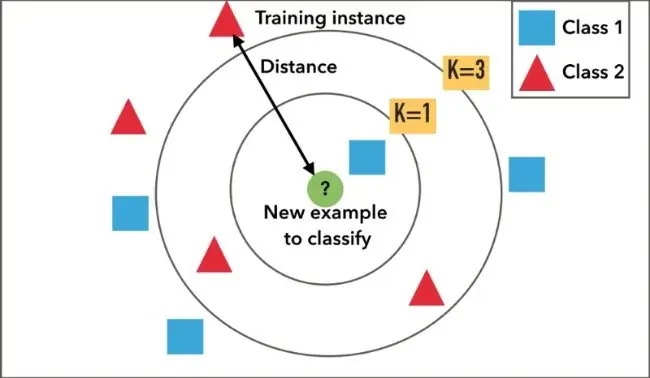
一、KNN原理分析
古语说得好,物以类聚,人以群分;近朱者赤,近墨者黑。这句话其实也就是K最近邻算法的核心思想,在衡量两个对象之间的相似性或差距时,一个直观的想法就是考虑它们之间的距离。在机器学习的聚类或分类任务中,距离的概念具有极其重要的意义。首先,我们定义一个训练集,它包含多个样本点,每个样本点都有一组特征和一个类别标签。具体来说,训练集可以表示为:
其中,\(x_i\)为实例样本的特征向量,\(y_i\)为实例样本的类别,取值为\(c_1,c_2,\cdots,c_l\),\(i=1,2,\cdots,N\),每一个 \(x_i=(x_{i1},x_{i2},\cdots,x_{in})\)都有 \(n\)个特征。
- 输入:训练数据集\(T = \{(x_1,y_1),(x_2,y_2),\cdots,(x_N,y_N)\}\)
- 输出:实例\(x\) 所属的类\(y\)
(1)根据给定的距离度量,在训练集 \(T\)中找出与\(x\) 最近邻的\(k\)个点,涵盖这个\(k\)点的\(x\)的邻域记作\(N_k(x)\)
(2)在\(N_k(x)\)中根据分类决策规则(如多数决策)决定 \(x\)的类别\(y\)
其中,\(I\)为示性函数,即\(y_i = c_j\)时\(I\)为 1,否则\(I\) 为 0
通过合理选择\(k\)值、距离度量方式和分类决策规则,\(k\)近邻法可以在分类任务中取得良好的性能。然而,由于它依赖于整个训练数据集进行预测,对于大型数据集,计算成本可能会很高。因此,在实际应用中,常常需要采用一些优化技术来提高\(k\)近邻法的效率和准确性。
KNN原理是:存在一个样本数据集合,也称作为训练样本集,并且样本集中每个数据都存在标签,即我们知道样本集中每一个数据与所属分类的对应关系。输入没有标签的新数据后,将新的数据的每个特征与样本集中数据对应的特征进行比较,然后算法提取样本最相似数据(最近邻)的分类标签。一般来说,我们只选择样本数据集中前k个最相似的数据,这就是\(k\)-近邻算法中k的出处,通常\(k\)是不大于20的整数。最后,选择k个最相似数据中出现次数最多的分类,作为新数据的分类。
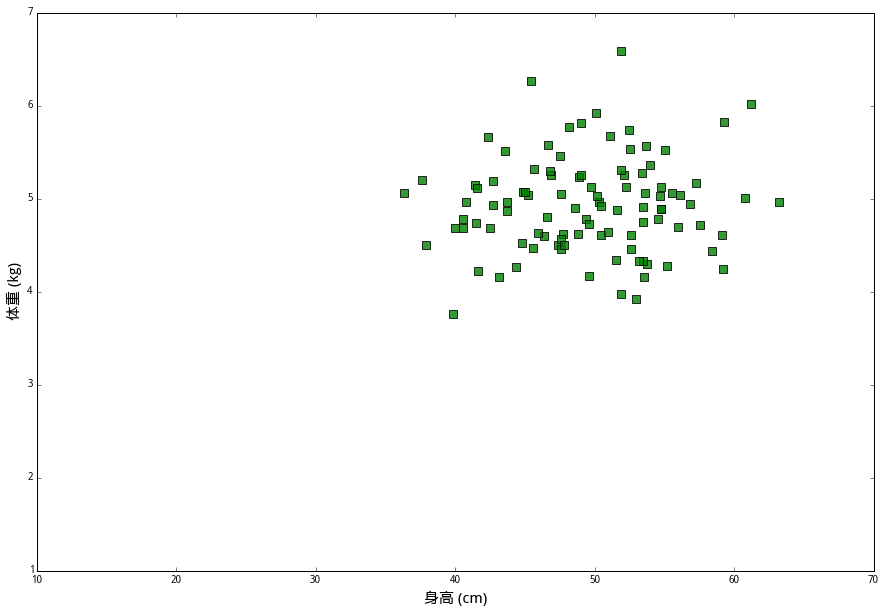
| 绿兔(Green),它们的平均身高是 50厘米,平均体重 5公斤 | 蓝兔(blue),它们体型比较小,平均身高是 30厘米,平均体重是 4公斤 | 黄兔(yellow),它们的平均身高45厘米,但体重较轻,平均只有2.5公斤 |
|---|---|---|
 |
 |
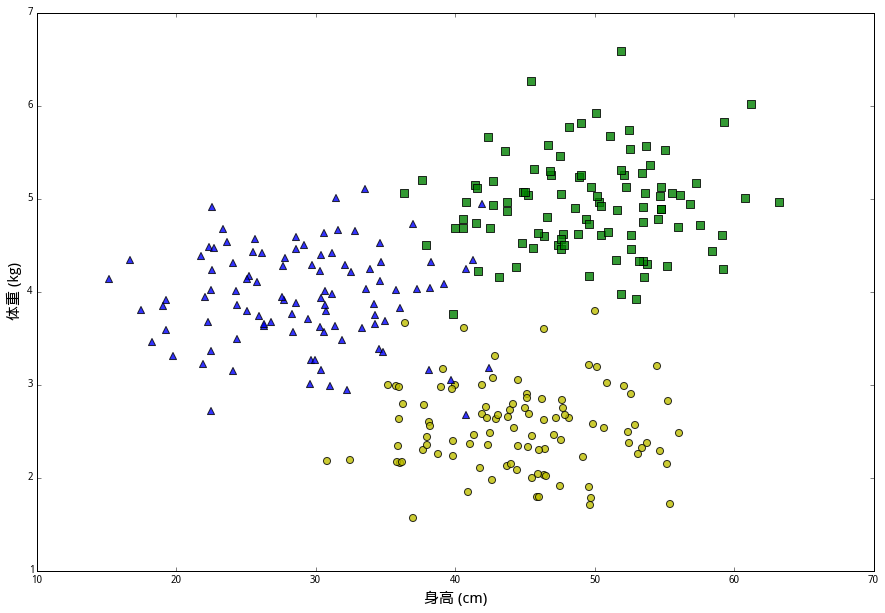 |
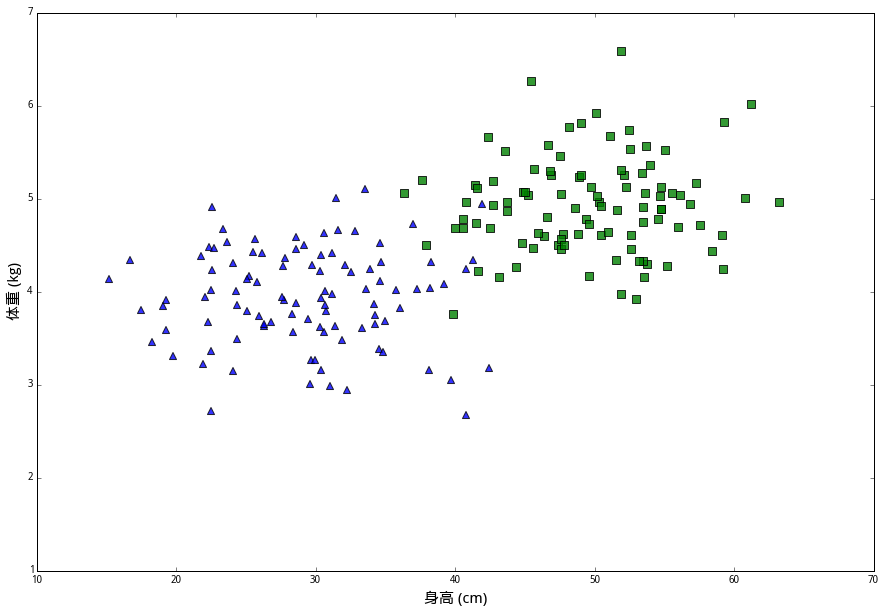
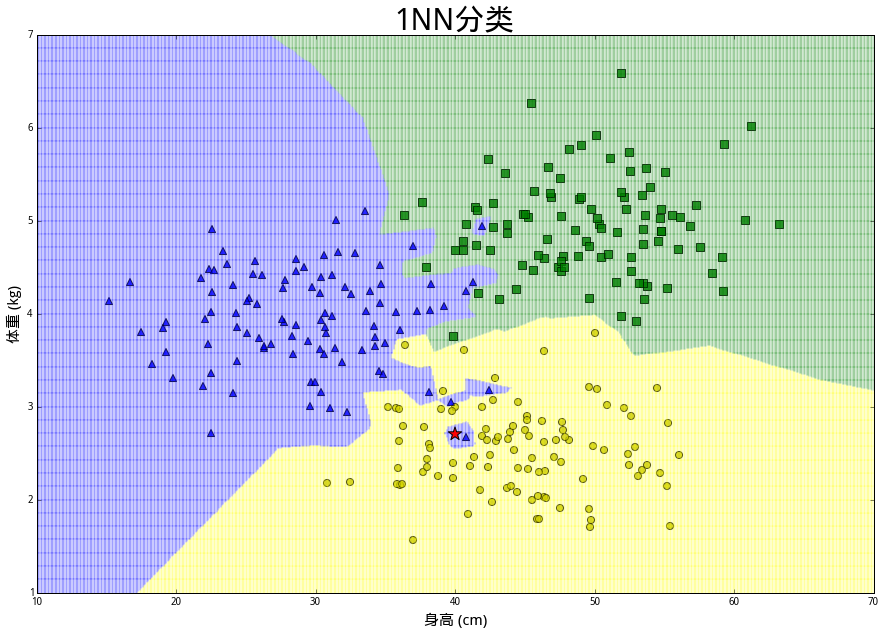
在上面数据中,(身高,体重)的二元组叫做特征(features),兔子的品种则是分类标签(class label)。我们想解决的问题是,给定一个未知分类的新样本的所有特征,通过已知数据来判断它的类别。现在假设有一只兔子R,想要确定它属于绿兔、蓝兔和黄兔中的哪一类,应该怎么做呢?按照最普通的直觉,应该在已知数据里找出几个和我们想探究的兔子最相似的几个点,然后看看那些兔子都是什么个情况;如果它们当中大多数都属于某一类别,那么兔子R大概率也就是那个类别了。为了确定兔子R属于哪一类,首先测量出其身长为 40 厘米,体重 2.7 公斤,为了直观展示,将其画在上述同一坐标系中,用红色五角星表示。现在预设一个整数\(k\),寻找距离兔子R最近的\(k\)个数据样本进行分析。kNN 算法如何对这次观测进行分类要取决于\(k\)的大小。直觉告诉我们兔子R像是一只黄兔,因为除了最近的蓝色三角外,附近其他都是黄色圆圈。如果设 \(k=15\),算法会判断这只兔子是一只黄兔。但是如果设 \(k=1\),那么由于距离最近的是蓝色三角,会判断兔子R是一只蓝兔。在两组分类中,1NN 的分类边界明显更“崎岖”,但是对历史样本没有误判;而 15NN 的分类边界更平滑,但是对历史样本有发生误判的现象。选择\(k\)的大小取决于对偏差和方差之间的权衡。
| 散点图 | \(k=15\) KNN | \(k=1\) KNN |
|---|---|---|
 |
 |
 |
二、算法思想与步骤
KNN算法思想可以用一句话概括:如果一个样本在特征空间中的\(k\)个最相似(即特征空间中最邻近,用上面的距离公式描述)的样本中的大多数属于某一个类别,则该样本也属于这个类别。该方法在定类决策上只依据最邻近的一个或者几个样本的类别来决定待分样本所属的类别。
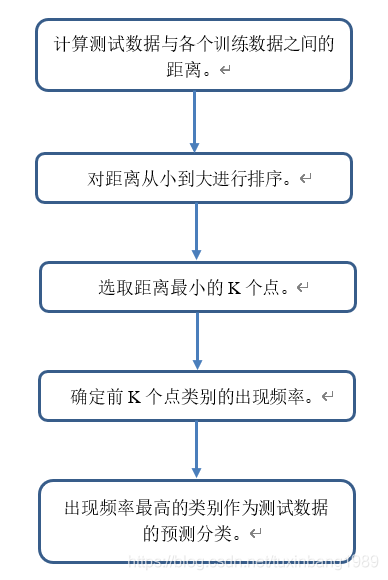
对于一组训练样本以及一个测试样本,算法步骤可以大致分为如下几个步骤:
计算已知类别数据集中的点与当前点之间的距离;
按照距离递增次序排序;
选取与当前点距离最小的k个点;
确定前k个点所在类别的出现频率;
返回前k个点出现频率最高的类别作为当前点的预测分类。
这里大致解释一下,比如我要预测\(x\)是属于哪一类,训练集里面有很多数据,我先算出\(x\)到其他所有点之间的距离,取前\(k\)个距离样本比较小的点,然后我们发现这\(k\)个点当中有5个属于class 1,\(k-5\)个属于class 2 ,那我们就直接比较5与\(k-5\)的大小然后判断\(x\)属于哪一类吗?这显然是是不合理的。这里毫无意外也需要体现加权的思想。如果那五个属于class 1的点相比于另外\(k-5\)个属于class 2的点,它们距离样本点更近,根据近朱者赤,近墨者黑的原则,毫无疑问样本点\(x\)属于class 1的可能性更大,也即是说,这五个点在最终决策当中应当占据更大的比重。那么怎么来体现这种加权呢?我们很容易想到距离占总距离的比重,但是这样的话距离大的反而权重较大,因此我们需要用1来减去该权重,得到最终的权重。我们把\(k\)个点当中属于class 1的权重加起来,再把属于class 2的权重加起来,谁的结果大,\(x\)就属于哪一类。
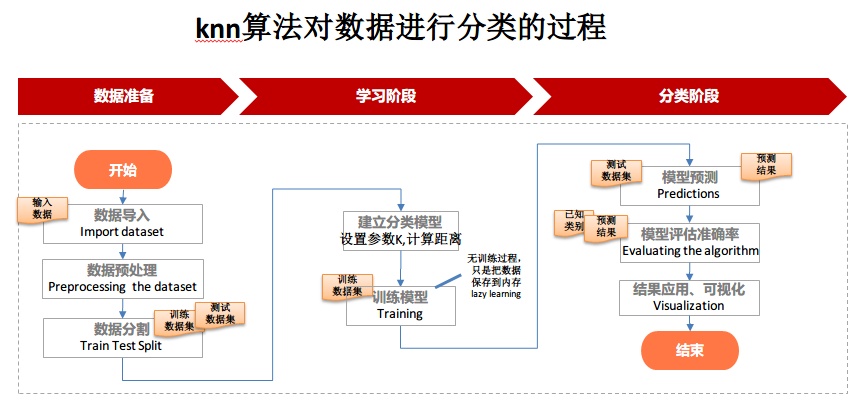
在KNN算法中,三个关键要素:\(k\)值的选择、距离度量和分类决策规则,对于算法的性能和效果至关重要。首先,让我们着眼于\(k\)值的选择。\(k\)值代表了在分类过程中要考虑的最近邻居的数量。选择合适的\(k\)值至关重要,因为它直接影响到模型的性能和泛化能力。较小的\(k\)值可能导致模型对训练数据过于敏感,产生过拟合的现象,而较大的\(k\)值则可能导致模型过于平滑,忽略了数据的局部特征,产生欠拟合。因此,我们需要通过交叉验证等技术来调优k值,以找到最适合数据集的值(选择合适k值的方法有:经验法则:初步尝试较小的k值(如3或5),并根据实验结果逐步调整。交叉验证:将数据集划分为多个子集,通过比较不同k值下模型在测试集上的性能,选择最优的k值。网格搜索:在指定的k值范围内系统搜索,选择性能最优的k值。启发式方法:采用一些启发式策略,如选择奇数值的k值或根据数据集大小选择k值。实验调优:通过实验观察模型在不同k值下的性能变化,选择合适的k值。)。其次,距离度量在kNN算法中起着至关重要的作用。它用于衡量数据点之间的相似性,从而确定最近邻居。常用的距离度量方式包括欧氏距离、曼哈顿距离和余弦相似度等。不同的距离度量方式适用于不同类型的数据和分类任务。例如,欧氏距离适用于连续型数值数据,而曼哈顿距离则更适用于稀疏数据或整数型数据。在选择距离度量方式时,我们需要考虑数据的特性和分类任务的需求,以确保选择的度量方式能够准确地反映数据之间的相似性。最后,分类决策规则决定了基于\(k\)个最近邻居的类别标签来做出最终分类决策的方法。常见的分类决策规则包括多数投票法和加权投票法。多数投票法是最简单也是最常用的方法,它选择\(k\)个最近邻居中出现次数最多的类别作为预测类别。而加权投票法则考虑了邻居与待分类样本之间的距离,给予距离较近的邻居更大的权重。选择合适的分类决策规则有助于提高模型的准确性和稳定性,因此在应用KNN算法时,我们需要仔细选择合适的决策规则,以获得更好的分类效果。综上所述,KNN算法中的k值选择、距离度量和分类决策规则是相互关联、相互影响的要素,它们共同决定了模型的性能和效果。通过合理选择这些要素,我们可以构建出更加准确、稳定的KNN分类器,从而应对各种不同的分类任务。
| 流程图1 | 流程图2 |
|---|---|
 |
![] |
三、算法实现
3.1 案例1
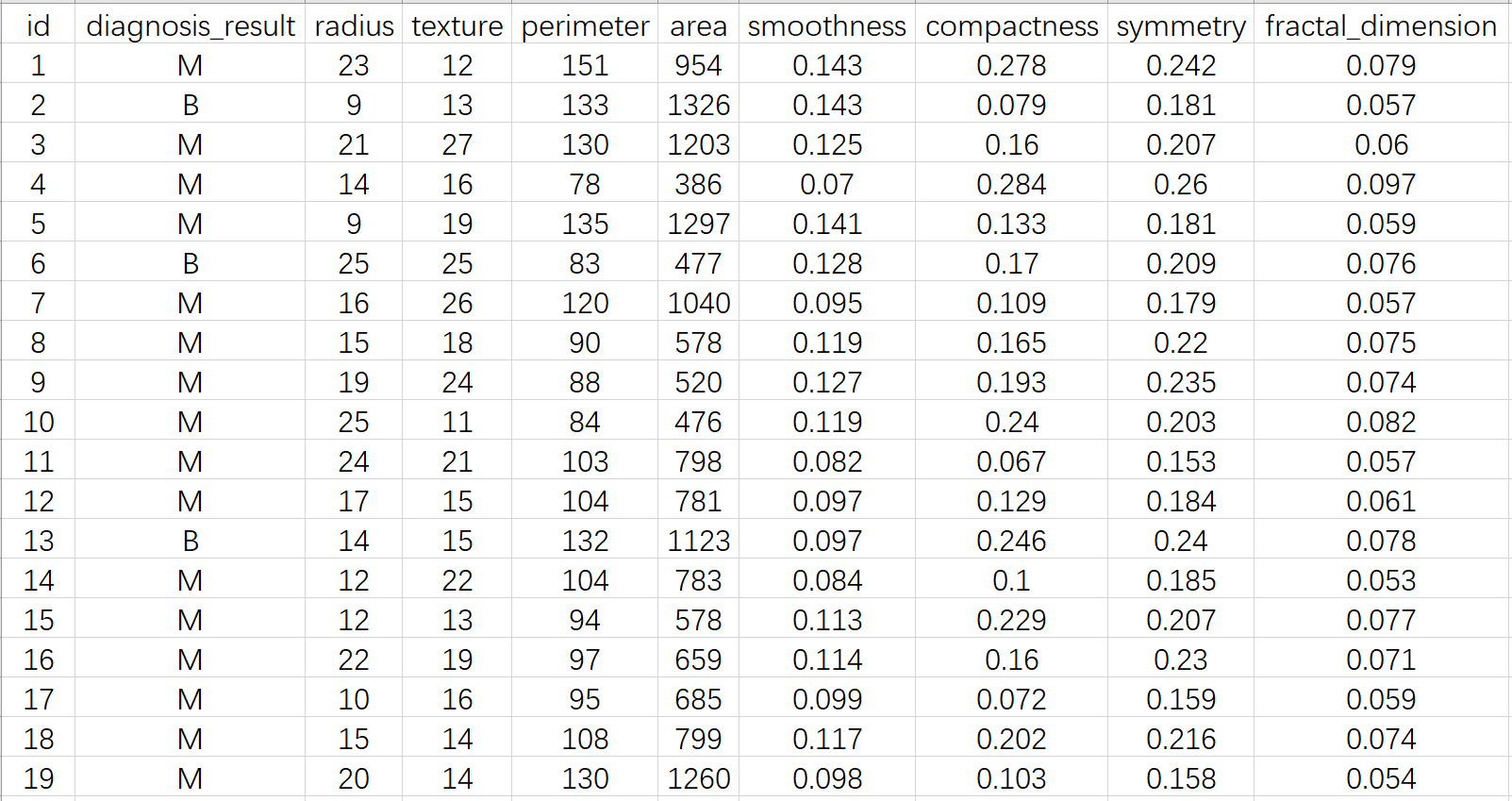
[数据文件Prostate_Cancer.csv下载链接](https://wwd.lanzoum.com/icOrE1whkr8b)
from sklearn.neighbors import KNeighborsClassifier
import numpy as np
import pandas as pd
from sklearn.metrics import confusion_matrix
import seaborn as sns
import matplotlib.pyplot as plt
def knn():
K = 8
data = pd.read_csv(r"Prostate_Cancer.csv")
n = len(data) // 3
test_set = data[0:n]
train_set = data[n:]
train_set = np.array(train_set)
test_set = np.array(test_set)
A = [i for i in range(0, len(train_set))]
B = [i for i in range(2, 10)]
C = [i for i in range(n)]
D = [1]
x_train = train_set[A]
x_train = x_train[:, B]
y_train = train_set[A]
y_train = y_train[:, D].ravel() # Reshape y_train to 1d array
x_test = test_set[C]
x_test = x_test[:, B]
y_test = test_set[C]
y_test = y_test[:, D].ravel() # Reshape y_test to 1d array
# Train the model
model = KNeighborsClassifier(n_neighbors=K)
model.fit(x_train, y_train)
# Predict the labels for the test set
y_pred = model.predict(x_test)
# Output predicted and true labels for the test set
print("Predicted labels:", y_pred)
print("True labels:", y_test)
# Generate confusion matrix
cm = confusion_matrix(y_test, y_pred)
# Plot confusion matrix
plt.figure(figsize=(8, 6))
sns.heatmap(cm, annot=True, cmap='Blues', fmt='g', cbar=False)
plt.xlabel('Predicted labels')
plt.ylabel('True labels')
plt.title('Confusion Matrix')
plt.show()
if __name__ == '__main__':
knn()
| 结果 | 混淆矩阵 |
|---|---|
| Predicted labels: ['M' 'M' 'M' 'B' 'M' 'B' 'M' 'B' 'B' 'B' 'M' 'M' 'M' 'M' 'B' 'M' 'M' 'M' 'M' 'B' 'B' 'B' 'M' 'M' 'M' 'M' 'M' 'M' 'M' 'M' 'M' 'B' 'M'] True labels: ['M' 'B' 'M' 'M' 'M' 'B' 'M' 'M' 'M' 'M' 'M' 'M' 'B' 'M' 'M' 'M' 'M' 'M' 'M' 'B' 'B' 'B' 'M' 'M' 'M' 'M' 'M' 'M' 'M' 'M' 'M' 'M' 'M'] | 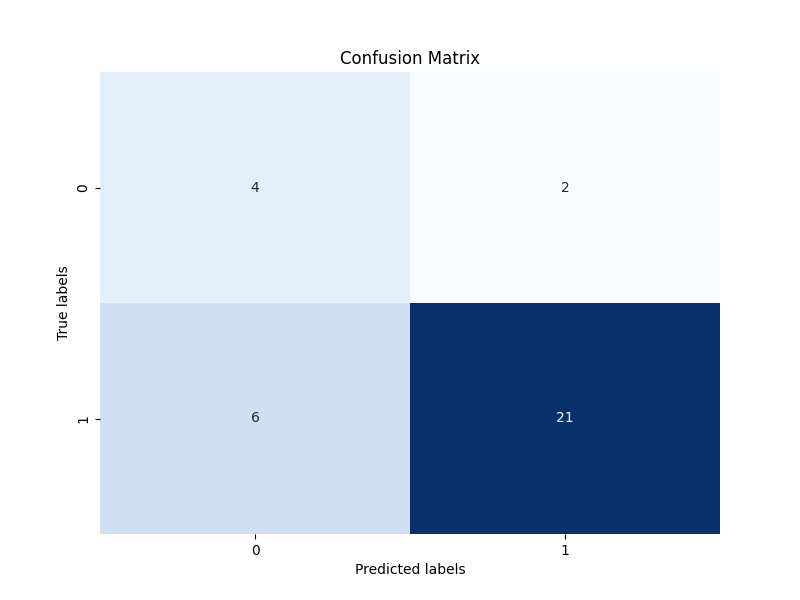 |
3.2案例2
import numpy as np
import pandas as pd
import matplotlib.pyplot as plt
import matplotlib as mpl
from sklearn.model_selection import train_test_split
from sklearn.metrics import accuracy_score
from matplotlib.colors import ListedColormap
#导入iris数据
from sklearn.datasets import load_iris
iris = load_iris()
X=iris.data[:,:2] #只取前两列
y=iris.target
X_train, X_test, y_train, y_test = train_test_split(X, y, stratify=y,random_state=42) #划分数据,random_state固定划分方式
#导入模型
from sklearn.neighbors import KNeighborsClassifier
#训练模型
n_neighbors = 5
knn = KNeighborsClassifier(n_neighbors=n_neighbors)
knn.fit(X_train, y_train)
y_pred = knn.predict(X_test)
#查看各项得分
print("y_pred",y_pred)
print("y_test",y_test)
print("score on train set", knn.score(X_train, y_train))
print("score on test set", knn.score(X_test, y_test))
print("accuracy score", accuracy_score(y_test, y_pred))
# 可视化
# 自定义colormap
def colormap():
return mpl.colors.LinearSegmentedColormap.from_list('cmap', ['#FFC0CB','#00BFFF', '#1E90FF'], 256)
x_min, x_max = X[:, 0].min() - 1, X[:, 0].max() + 1
y_min, y_max = X[:, 1].min() - 1, X[:, 1].max() + 1
axes=[x_min, x_max, y_min, y_max]
xp=np.linspace(axes[0], axes[1], 500) #均匀500的横坐标
yp=np.linspace(axes[2], axes[3],500) #均匀500个纵坐标
xx, yy=np.meshgrid(xp, yp) #生成500X500网格点
xy=np.c_[xx.ravel(), yy.ravel()] #按行拼接,规范成坐标点的格式
y_pred = knn.predict(xy).reshape(xx.shape) #训练之后平铺
# 可视化方法一
plt.figure(figsize=(15,5),dpi=100)
plt.subplot(1,2,1)
plt.contourf(xx, yy, y_pred, alpha=0.3, cmap=colormap())
#画三种类型的点
p1=plt.scatter(X[y==0,0], X[y==0, 1], color='blue',marker='^')
p2=plt.scatter(X[y==1,0], X[y==1, 1], color='green', marker='o')
p3=plt.scatter(X[y==2,0], X[y==2, 1], color='red',marker='*')
#设置注释
plt.legend([p1, p2, p3], iris['target_names'], loc='upper right',fontsize='large')
#设置标题
plt.title(f"3-Class classification (k = {n_neighbors})", fontdict={'fontsize':15} )
# 可视化方法二
plt.subplot(1,2,2)
cmap_light = ListedColormap(['pink', 'cyan', 'cornflowerblue'])
cmap_bold = ListedColormap(['darkorange', 'c', 'darkblue'])
plt.pcolormesh(xx, yy, y_pred, cmap=cmap_light)
# Plot also the training points
plt.scatter(X[:, 0], X[:, 1], c=y, cmap=cmap_bold,
edgecolor='k', s=20)
plt.xlim(xx.min(), xx.max())
plt.ylim(yy.min(), yy.max())
plt.title(f"3-Class classification (k = {n_neighbors})" ,fontdict={'fontsize':15})
plt.show()
| 结果 | 聚类图 |
|---|---|
| y_pred [0 2 2 1 0 2 1 2 2 2 1 2 1 1 0 0 0 1 0 1 1 1 1 2 1 1 0 1 0 1 1 1 0 0 0 0 2 1] y_test [0 1 1 1 0 1 2 2 2 2 2 2 1 1 0 0 0 1 0 1 2 1 2 1 2 1 0 2 0 1 2 2 0 0 0 0 2 1] | 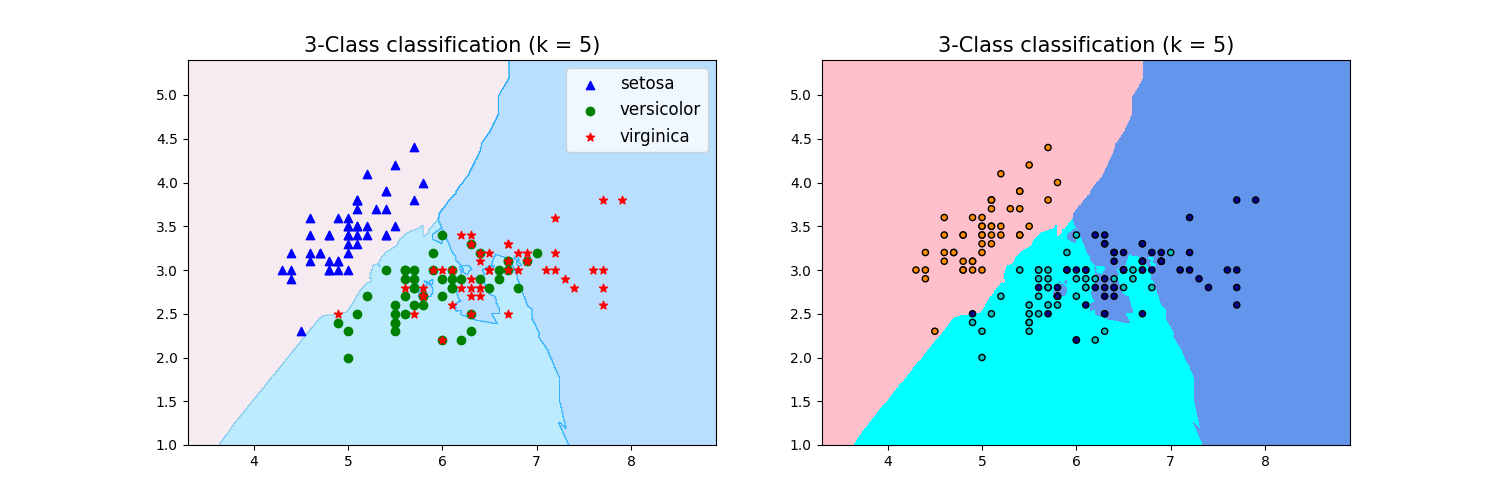 |
3.3 案例3
import sklearn.datasets as datasets # 导入数据库
from sklearn.neighbors import KNeighborsClassifier # 导入KNN分类算法
from sklearn.model_selection import train_test_split # 导入数据集划分器
# 1.捕获鸢尾花数据
iris = datasets.load_iris()
# 2.提取样本数据
feature = iris['data'] # 特征数据
target = iris['target'] # 目标数据
# 3.对数据集进行拆分
x_train, x_test, y_train, y_test = train_test_split(feature, target, test_size=0.2, random_state=2021)
# 4.观察数据集:检查是否需要进行特征工程的处理
print(x_train) # 第一检查特征数据是否都是数值型数据(特征抽取),第二检查特征数据之间大小的差距(特征预处理),第三检查特征数据的维度(特征选择) 一般情况下从datasets中捕获的数据是不需要做特征工程的处理的
# 5.实例化模型对象(在KNN中k取值的不同会直接导致模型的分类结果的不同,因此k也可以被称为模型的超参数)
knn = KNeighborsClassifier(n_neighbors=3) # n_neighbors == k
# 6.使用训练集数据训练模型(参数内容:训练集的特征数据以及训练集的标签数据,其中要求训练集的特征数据必须是二维的)
# print(x_train.shape) # (120, 4)
knn = knn.fit(x_train, y_train)
print(knn) # 打印训练的结果
# 7.使用测试数据,测试模型(参数内容:测试集的特征数据) .predict表示使用训练好的模型实现分类或者预测
y_pred = knn.predict(x_test) # 模型基于测试数据返回的分类结果
y_true = y_test # 测试集真实的分类结果
print('模型的分类结果:', y_pred)
print('真实的分类结果:', y_true)
# 8.预测、分类结果的评分
print(knn.score(x_test, y_test)) # 0.9666666666666667
# 结果 (29/30)
# 模型的分类结果: [0 0 1 0 0 0 0 0 0 0 0 1 2 2 1 2 1 1 0 1 1 2 2 0 2 1 1 2 0 0]
# 真实的分类结果: [0 0 1 0 0 0 0 0 0 0 0 1 2 2 1 2 1 1 0 1 1 2 2 0 2 1 1 1 0 0]
# 注:在改变k值(n_neighbors)之后,不论是分类预测的结果还是评分都会发生改变
# 当出现一个未知分类的鸢尾花时,对其的分类进行预测
test1 = knn.predict([[6.1, 3.1, 4.7, 2.1]])
print(test1)
# 结果 [2] , 也就是将该未知分类的鸢尾花分为了第二类鸢尾花
总结
KNN算法的优点之一是简单易懂,不需要对数据进行假设或训练模型,因此适用于各种数据类型和领域。然而,KNN算法的缺点之一是计算复杂度高,尤其是当训练集很大时。此外,KNN对于输入特征的规模和单位很敏感,因此在使用之前需要进行特征缩放或规范化。KNN算法有广泛的应用场景,以下是一些典型的例子:
分类问题:KNN算法可用于分类问题,如文本分类、图像分类等。在文本分类中,可以使用KNN算法来根据文本的特征将其归类到不同的类别,例如垃圾邮件过滤、情感分析等。在图像分类中,KNN算法可以通过比较图像的像素值来识别图像中的对象或场景。
推荐系统:KNN算法在推荐系统中发挥着重要作用。基于用户行为或偏好的相似性,KNN可以推荐给用户与其兴趣相似的产品或内容。例如,在电子商务平台上,可以使用KNN算法来向用户推荐与其购买历史相似的产品。
异常检测:KNN算法可用于异常检测,即识别数据集中与其他数据点不同的观测值。通过计算数据点与其最近邻的距离,可以判断其是否属于正常的数据分布。异常检测在金融领域、网络安全等方面具有重要应用。
回归问题:除了分类问题,KNN算法也可用于回归问题,如房价预测、股票价格预测等。在这种情况下,KNN算法预测的是一个连续值而不是一个类别标签。通过计算新数据点与已有数据点的距离加权平均值,可以预测出新数据点的值。
医学诊断:KNN算法在医学领域中被广泛应用于疾病诊断和预测。通过比较患者的特征与已知病例的相似性,可以帮助医生做出诊断或预测疾病的发展趋势。例如,可以使用KNN算法来根据患者的生理指标和医疗历史来预测患者患某种疾病的可能性。
总的来说,KNN算法是一种简单而灵活的机器学习算法,适用于各种不同类型的问题和数据。它的简单性和有效性使其成为许多实际应用中的首选方法之一。然而,在使用KNN算法时需要注意选择合适的距离度量方式和K值,以及处理好数据的特征缩放和规范化问题,以获得更好的预测性能。
参考资料
| 距离类型 | 公式 | 描述 |
|---|---|---|
| 欧式距离 | \(d=\sqrt{(x_1-x_2)^2 + (y_1-y_2)^2}\) | 两点在二维空间中的直线距离 |
| 余弦距离 | \(d=\frac{x_1 \cdot x_2 + y_1 \cdot y_2}{\sqrt{x_1^2 + y_1^2} \cdot \sqrt{x_2^2 + y_2^2}}\) | 两个向量的夹角余弦值 |
| 曼哈顿距离 | \(d=|x_1-x_2|+|y_1-y_2|\) | 两点在标准坐标系上的绝对轴距总和 |
| 切比雪夫距离 | \(d=\max(|x_1-x_2|, |y_1-y_2|)\) | 两点之间各维度上的数值差的最大值 |
| 闵氏距离 | \(d=\left[(x_1-x_2)^p + (y_1-y_2)^p\right]^{\frac{1}{p}}\) | 两点在n维空间中的距离,p为参数 |
| 标准化欧氏距离 | \(d=\sqrt{\sum\left(\frac{x_i}{s_i}-\frac{x_j}{s_j}\right)^2}\) | 标准化后的欧式距离,\(s_i\)和\(s_j\)为各分量的标准差 |
| 马氏距离 | \(d=\sqrt{(x-\mu)^T\Sigma^{-1}(x-\mu)}\) | 数据的协方差距离,\(\Sigma\)是协方差矩阵 |
| 汉明距离 | \(d=\sum(x_i \oplus x_j)\) | 两个等长字符串对应位置的不同字符的个数 |
| 巴氏距离 | \(d=-\ln(BC(p,q))\) | 在概率统计中,用来度量两个离散概率分布的差异程度 |



 浙公网安备 33010602011771号
浙公网安备 33010602011771号