博弈论——信息经济学逆向选择（十四）

逆向选择是指由于信息的差异性或非对称性而导致的市场失灵现象，具体是指在市多交易双方中，参与交易的一方持有某些与交易相关的信息而另一方却不能直接或者间线完全知晓，而且不知情的一方对他方的信息由于验证信息成本的昂贵使得验证在经济上环现实或是不合算，在这种情况下，拥有信息优势的一方有可能隐藏自已的私人信息，甚至借此向他人提供不真实的信息以获取私利。或者逆向选择是指信息不对称的市场会把优秀的资源赶出局，而不是把低劣的资源淘汰掉，从而导致市场运作无效率的现象。乔治·阿克劳夫（George Akerlof）在1970年发表了名为《柠檬市场：质量不确定性和市场机制》的论文，被公认为是信息经济学中最重要的开创性文献。在美国俚语中，“柠檬”俗称“次品”，这篇研究次品市场的论文因为浅显先后被三、四杂志退稿。然而，乔治·阿克洛夫 （George Akerlof）在这篇论文中提出的逆向选择理论揭示了看似简单实际上又非常深刻的经济学道理。

一、逆向选择案例

1.1 二手车市场

在二手车市场上，卖方较为全面地掌握着有关旧车性能的信息，而买方则对此信息知之甚少。这样当性能较好的旧车与性能较差的旧车同时出现在交易市场上时，由于潜在买方缺乏信息量而降低其分辨能力，他在购买时选择的可能是性能较差的旧车。整个交易的结果是一些性能较好的旧车卖不出去，而一些性能较差的旧车可能被买走。
旧车市场逆向选择问题来自买者和卖者有关车的质量信息不对称。在旧车市场，卖者知道车的真实质量，而买者不知道。这样卖者就会以次充好，买者也不傻，尽管他们不能了解旧车的真实质量，只知道车的平均质量，愿平均质量出中等价格，这样一来，那些高于中等价的上等旧车就可能会退出市场。接下来的演绎是，由于上等车退出市场，买者会继续降低估价，次上等车会退出市场；演绎的最后结果是：市场上成了破烂车的展览馆，极端的情况一辆车都不成交。现实的情况是，社会成交量小于实际均衡量。这个过程称为逆向选择。

1.2 保险市场

在保险市场中，保险合同的缔约双方之间存在着不容忽视的信息差别，这个事实已经并且将继续妨碍着某些高效合同的签订。例如，假定参加人寿保险的社会成员根据意外事件的不同概率被划分为不同的风险类别，保险公司仅仅知道投保人在某类意外事件的平均风险。又假设每个希望保险的社会成员都知道他属于哪个风险类别的成员，因而也了解其承担风险的概率。但是，保险公司不能准确地按照投保人的真实风险水平区分投保人。由于受到这种约束，保险公司只能向所有投保人提出大致相同的保险费用。因此，在保险公司任何指定的价格水平上，高风险的社会成员将购买更多保险，而低风险的个人必然购买更少的保险。结果，保险统计的预期与所有参加保险者同等参与的结果相比，或者与不同风险水平支付不同保险费用这样一种理想模式的结果相比，保险公司所处的选择境况更为不利。在实际操作中，保险公司为了避免这种窘境不得不投人大量人力、物力和财力收集投保人私人信息，然而，这样做只能降低或减缓保险公司的不利选择程度，风险并没有由此得到有效分担。再比如愿意参加保险的人很可能是身体有问题的人。身体是否有问题，投保人比保险公司更清楚，也就是说，投保人具有私人信息。保险公司知道这点，就把保险费定得很高，这样，身体好的人就更不愿参加保险，这部分人就退出了市场。所以，热衷于买保险的人往往是身体不好或年龄较大的人。因此，保险公司不能从根本上消除逆向选择境况，社会风险承担的均衡配置将是低效率的。

1.3 劳动力市场

逆向选择是指雇主在不了解可能对自己产生不利影响的信息情况下，与雇员签订合同所面临的对己不利的困境。劳动力市场上供求双方为了追求利益最大化，都会尽力改善自己的不利处境，主要表现为对信息的搜寻。一是劳动者的搜寻。在劳动市场，由于同质劳动力的工资率是离散的，因此，劳动者的搜寻是必要的、有益的。如果信息是免费的，搜寻将无限进行下去直到同质劳动的工资离散完全消失。但在实际中，搜寻会受到成本因素的制约，搜寻活动应在搜寻的预期边际收益等于边际成本时停止。二是雇主的统计歧视。同样，雇主也会尽力搜寻雇员的信息，但递增的信息成本会阻止雇主作过多的考察，雇主只能根据某些易于判断的特征(如文凭、性别)对雇员进行等级划分，每一等级以雇员的平均能力为依据制定统一工资标准，这样就导致了“统计歧视”。由于统一工资水平对低素质雇员具有吸引力，从而又导致一部分高素质雇员离开，这样就形成了劳动力市场的逆向选择。

1.4货币市场

在货币市场上项目是否有风险是借款人的私人信息，因此，贷款人对贷款利率的出价是一个平均风险水平的价格，于是风险低收益低的稳定型借款者就会逐步退出市场。这样银行的坏账就会一天天增加。在资本市场上，每个借贷者要求同样数目的贷款条件下，银行不能将借款者按照回报率的大小给予不同的利息率。银行能否收回贷款并获得利润，既取决于借款者的经济效益，也取决于银行所处环境状态的各种不确定性。如果银行以借款者的经济收益作为利息率标准，那么借款者就会利用银行难以观察或不可能观察到的信息做出对策，比如虚报利润额、人为地扩大成本等，由此在一定程度上减少银行承担的风险。但是，银行借贷的预期仍然存在着许多不确定结果，如借款者难以抗拒的风险力量，借款者破产或携款逃亡等。因此，所有的信贷活动都涉及借款者因主观或客观原因丧失清偿能力的违约风险。显然，正是银行与借款者之间信息的非对称性，才出现了使作为委托人的银行不利的市场选择境况。
为了避免不利选择的结果，市场参加者都试图明确产品或服务价格与质量之间的关系。斯彭塞将这种关系用“市场信号”的概念来描述。阿罗则认为，通过有效的信息收集，人们能够直接认识到不利选择的内容，并相应地限制这类现象的出现。保险公司也发现，从事信息收集和建立高效率的信息系统以减少不利选择的范围是一项有利可图的工作。在资本市场上，银行系统活动中的相当部分就是准确地收集有关潜在债务人的信息，并对借款者进行间接的信息控制，从中限制不利选择的范围。

二、二手车市场逆向选择分析

阿克洛夫的旧车市场模型可以简单概括如下。有多个潜在的卖者和多个潜在的买者, 卖者知道自己出售的车的质量 \(\theta\), 买者不知道 \(\theta\), 但知道 \(\theta\) 的分布函数 \(F(\theta)\); 买者出价 \(P\), 卖者决定接受或不接受; 如果接受, 买者的效用为 \(\pi_B=V(\theta)-P\), 卖者的效用为 \(\pi_s=P-U(\theta)\); 如果不接受, 双方的效用均为零。这里, \(V(\theta)\) 为买者的评价, \(U(\theta)\) 为 卖者的评价, 也就是各自的效用, 且 \(\partial V / \partial \theta>0, \partial U / \partial \theta>0, V(\theta) \geq U(\theta)\) (否则, 交易没有意义）。注意，我们已将没有交易发生时的效用水平标准化为零，因而交易带来 的效用是指净效用: 买者从质量为的 \(\theta\) 车中得到的总效用为 \(V(\theta)\), 支付的价格为 \(P\), 因而 净效用为 \(\pi_B=V(\theta)-P\); 卖者从出售旧车得到的货币收入为 \(P\), 失掉车的效用损失为 \(U(\theta)\), 因而净效用为 \(\pi_s=P-U(\theta)\) 。此外, 我们还假定买者和卖者都是风险中性的。

2.1 两类卖主且买卖双方有相同的偏好

让我们首先考虑最简单的情况。假定卖者出售的车有两种可能的类型: \(\theta=6000\) 高质 量）或 \(\theta=2000\) (低质量）, 每一种的概率分别为二分之一; 买卖双方有相同的偏好且对 车的评价等于车的质量: \(V(\theta)=U(\theta)=\theta\) 。那么, 如果没有交易发生, 支付为效用向量 \((0,0)\), 如果在价格 \(P\) 下成交, 买者的效用为 \(\pi_B=\theta-P\), 卖者的效用为 \(\pi_s=P-\theta\), 显 然, 如果买者知道车的质量, 均衡价格为 \(P=6000\) (高质量), 或 \(P=2000\) (低质 量)。当买者不能知道车的质量时, 如果两类车都进入市场, 车的平均质量为 \(\mathrm{E} 0=4000\), 买者愿意出的最高价格为 \(P=4000\); 但在此价格下, 高质量车的卖者将退出市场（因为 \(\pi_s=4000-6000<0\), 只有低质量车的卖者愿意出售（因为 \(\pi_s=4000-2000>0\) 。买者知道, 愿意出售的卖者一定是低质量的卖者, 因此 \(P=4000\) 不可能是均衡价格, 唯一的均衡是 \(P=2000\), 只有低质量的车成交, 高质量的车退出市场。
有没有可能高质量的车主在等待低质量的卖完后再进入市场以 \(P=6000\) 成交, 因为此时每一个人都知道没有卖出去的都是高质量的车? 答案是否定的, 因为如果预期到这种情 况会发生，低质量车的卖者就会等待价格上升后再出手，我们又回到了原来的状态。
这个例一子尽管简单, 但给出了逆向选择的基本含义:坏车将好车驱逐出市场。这与货 币史上 “劣币驱逐良币” 故事是同一个道理。现实中这样的例一子比比皆是, 比如说, 如果小流氓都留光头, 一个正派的人就不会留光头, 即使他本来也喜欢光头（或许因为光头洗起来方便），这里，小流氓把正派人驱逐出光头队伍。在学术市场上，如果一个杂志老是发表低质量的文章, 真正有水平的学者就不会向这个杂志投稿, 这里, 低质量的文章把高质量的文章驱逐出这本杂志。

2.2卖主的类型是连续分布且买卖双方偏好相同

在上例中, 车的质量只有两种类型。现在我们考虑车的质量 \(\theta\) 为连续分布的情况。假 定 \(\theta\) 在 \([2000,6000]\) 区间上均匀分布, 密度函数 \(f(\theta)=1 /(6000-2000)=1 / 4000\), 偏好 函数与上例相同。那么, 如果所有的车都在市场上, 买者预期的质量为 \(\bar{\theta}=4000\), 愿意支 付的价格也是 4000 。但此时, 只有 \(\theta \leq 4000\) 的卖者才愿意出售, 所有 \(\theta>4000\) 的卖者都 将退出市场。结果, 市场上车的平均质量由 4000 降到 3000 , 买者愿意付的价格也由 4000 降到 3000。但在价格为 3000 时, 只有 \(\theta \leq 3000\) 的卖者愿意出售, 所有 \(\theta>3000\) 的卖者 都退出市场, 留在市场上的车的平均质量进一步下降到 2500 , 如此等等。我们有唯一的均衡价格是 \(P=2000\), 此时, 只有最低质量的车成交, 所有 \(P>2000\) 的车都退出市场。进一步, 因为 \(\theta\) 是连续分布的, \(\theta=2000\) 的概率为零, 整个市场消失了。
如果我们围需求曲线表示买者愿意支付的最高价格与市场上车的平均质量的关系，供给曲线表示市场上车的平均质量与价格的关系, 上述结论也可以用供求曲线来说明。此时, 需求曲线为 \(P=\bar{\theta}\), 供给曲线为:

\[\bar{\theta}=\frac{\frac{1}{4000} \int_{2000}^P \theta d \theta}{\frac{1}{4000} \int_{2000}^P d \theta}=\frac{P}{2}+1000, \quad \theta \in[2000,6000] \]

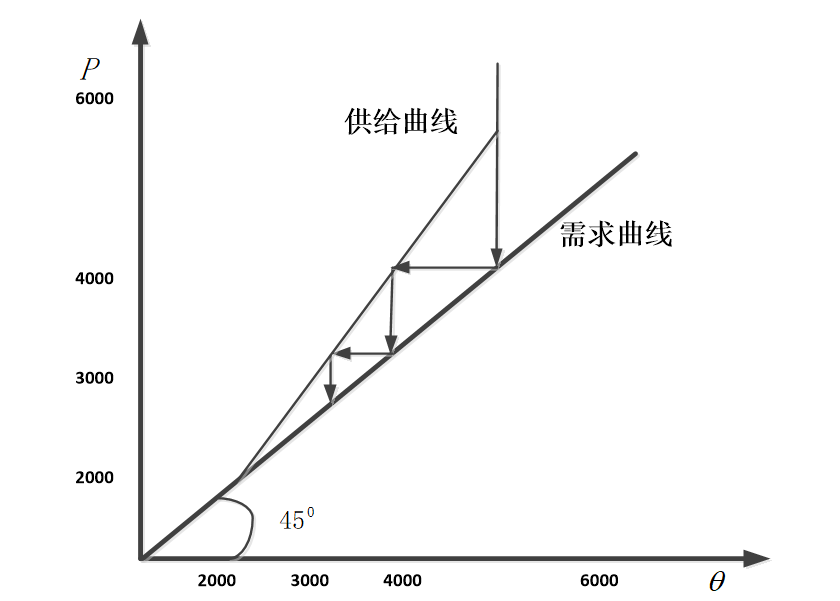
上述供给曲线意味着，尽管市场上出售的车的平均质量随着价格的上升而上升，但平均质量上升的幅度小于价格上升的幅度, 因为均衡意味着价格等于平均质量, 均衡价格一定在过原点的 \(45^{\circ}\) 线上, 即 \(P=\bar{\theta}=2000\), 如图所示 (图中, 需求曲线的斜率为 1 , 供给曲线的斜率为 2 , 唯一的交点是 2000)
上述供求曲线也可以转化为供给量和需求量与价格的关系。如通常情况下一样，供给曲线是向上倾斜的, 因为价格越高, 愿意出售的卖者越多。但与通常情况不同, 需求曲线可能向上倾斜而不是向下倾斜, 这是因为, 给定效用函数, 较高的价格诱导出较高的质量, 从而诱导出较多的买者。这一点并不意味着传统微观经济学的需求理论是错误的。传统需求理论假定产品质量是给定的, 与价格无关。但在这里, 质量与价格有关。当然, 一般来说, 需求曲线的准确形状依赖于两种因素的共同作用, 可能向上倾斜, 也可能向下倾斜。

2.3二手车市场的“劣币驱逐良币”

假定市场上有两群人，一群人是卖主，称为集团1，集团1的每一个人都拥有一辆二手车。另一群人是潜在买主，称为集团2。集团2每一个潜在买主的效用函数为\(u_2=M+\frac{3nq}{2}\)，\(M\)是旧车以外的消费，\(q\)是质量，\(n\)是一个0-1变量，表示买与不买。
①买者的决策
潜在买者面对着预算约束\(y_2=M+pn\)，表示潜在买主的全部收入可以只用来购买车以外的东西，也可以买车再把剩余的钱花在车以外的东西上。注意二手车价格\(p\)是唯一的，这是信息不对称的结果，由于买主并不知道想买的二手车的质量，所以鱼龙混杂，于是产生了逆向选择问题。买主的购买决策具有不确定性。写出买主的期望效用函数

\[E(u_2)=M+\frac{3}{2}nE(q)=M+\frac{3}{2}n\mu \]

其中\(\mu=E(q)\)是质量的均值，假定买主知道二手车市场的平均质量是\(\mu\)，代入预算约束得

\[E(u_2)=y_2+[\frac{3}{2}\mu-p]n \Rightarrow p \leq\frac{3}{2}\mu \]

时潜在的购买者会选择购买二手车。
②卖者的决策
卖主的效用函数\(u_1=M+nq\)，预算约束\(y_1=M+pn\)，注意这里卖主对二手车的“评价系数”，也即\(qn\)项前的系数，要低于买者的系数，说明买者的需求相比卖者的需求更为迫切，所以如果\(q\)的信息公开，\(p\)处在1到\(3/2\)之间时，双方是双赢的局面，但是问题在于\(q\)的信息是隐蔽的，妨碍了有效率的资源配置实现。
卖者的决策分析：\(q\)对卖者是明确的，所以卖者并不需要取期望效用，直接代入预算约束有

\[u_1=y_1+(q-p)n \Rightarrow q>p \]

时卖者不卖，\(q\leq p\)时卖者会选择出手。
③逆向选择的发生过程
假设：市场上的车质量服从\(U[0,2]\)的均匀分布，0表示质量最差的车，2表示质量最好的车。买主知道这样的分布立即得到\(\mu=1\)，所以按照前面的结论，买主能给出的最高出价是\(p=\frac{3}{2}\)。卖主知道买主最高只能出价到\(p=\frac{3}{2}\)，所以质量较好的车必然退出市场，所以市场上的车变为了\(U[0,\frac{3}{2}]\)。买主知道市场上好的车会因为出价低而退出，所以得到\(\mu=\frac{3}{4}\)，买主现在能给出的最高出价只有 \(\frac{9}{8}\)。
以此类推.....，卖主第\(n\)次退出后市场上的车变为

\[U[0,2\cdot(\frac{3}{4})^n]，\quad \lim_{n\rightarrow\infty}2\cdot(\frac{3}{4})^n=0 \]

意味着最后所有车都将退出市场，完全没有交易，市场彻底萎缩！
④Akerlof模型中市场失灵的根源来自于价格充当了双重功能：一方面，价格决定了供货者产品的平均质量，另一方面价格又决定了二手车质量在供求之间的均衡。解决逆向选择问题的办法是：需求方的出价适当提高，以及买者与卖者互相信任，通过合约或者法律对双方的行为做出约束，从而降低质量的不确定性，以提高分配的效率。

三、信息甄别模型

在信息不对称的情况下，Screening（筛选）和 Signaling（信号传递）是两种常见的机制设计方法，用于解决逆向选择问题。
Screening 是指信息不对称的“无信息方”设计合同或机制，以便从对方获得私人信息。通常是卖方（或合同提供方）不知道买方（或参与者）的私人信息，但通过设计合同或定价方案，迫使买方根据其类型作出不同的选择，从而揭示其信息。例如，卖方可能提供不同的产品或服务套餐（例如，定价和数量），以筛选出不同类型的消费者。通过这种方式，卖方可以推测买方的类型，并根据买方的选择来调整合同内容，从而减少信息不对称。
与此相对，Signaling 是指“有信息方”通过选择特定的行为或策略来向对方传递自己的私人信息。在这种情况下，信息较为充分的一方（通常是买方）主动向对方（通常是卖方）发出信号，以证明其类型。例如，求职者可能通过提供高学历、工作经验或专业证书等方式来向雇主传递自己的能力，雇主根据这些信号做出招聘决策。信号的选择和展示往往具有成本，确保信号的可靠性和价值。
Screening 是无信息的一方通过合同设计筛选信息，而 Signaling 是有信息的一方主动传递信息。两者都是应对信息不对称的有效手段，旨在减少逆向选择带来的不利影响。

在逆向选择模型中，卖家无法直接知道买家的类型，只能通过其行为（如购买数量或支付的金额）来推测买家的类型。本模型引入了信息甄别机制，通过设计价格、产品数量或入门费等方式，使得卖家能够通过买家的选择来甄别其类型。

3.1 基本假设

买家的效用可以表示为：

\[U(q, T, \theta) = \theta v(q) - T \]

其中：

• $ q $ 是买家购买的商品数量，
• $ T $ 是支付给卖家的总金额，
• $ v(q) $ 是买家在 $ q $ 单位商品中获得的效用，
• $ \theta $ 是买家的类型，且为买家的私有信息，卖家只知道 $ \theta $ 的分布 $ F $。

假设 $ v(q) = q^2 $，且 $ v(0) = 0 $。

卖家的效用为：

\[\pi = T - cq \]

其中 $ c $ 是商品的成本。

3.2 卖家的最优化问题

卖家的目标是设计合适的价格 $ T(q) $ 和商品数量 $ q $，以便最大化其效用，同时通过价格和数量的选择来迫使买家透露其类型。卖家要考虑的约束包括：

• 买家参与的约束（买家不愿意参与的情况下，卖家没有收入），
• 激励相容约束（保证买家选择他们的真实类型，即通过购买数量或支付价格来传递类型信息）。

参与约束保证了每个买家都愿意参与交易：

\[\theta_i v(q_i) - T_i \ge 0 \]

这一约束要求买家的效用至少为零，即买家不会在支付费用 $ T_i $ 后感到亏损。

激励相容约束确保了不同类型的买家根据其类型选择不同的购买数量 $ q_i $，即高需求类型的买家不会伪装成低需求类型的买家，反之亦然。卖家通过价格和数量的设置使得不同类型的买家在参与时选择符合其真实类型的行为。

对于不同类型的买家 $ i $ 和 $ j $，我们要求：

\[\theta_i v(q_i) - T_i \ge \theta_i v(q_j) - T_j \quad (\text{for } i \neq j) \]

通过整理该约束，得到：

\[(\theta_i - \theta_j)(v(q_i) - v(q_j)) \ge 0 \]

即：

\[\theta_i \ge \theta_j \implies q_i \ge q_j \]

这意味着卖家需要确保较高类型的买家选择更高的购买数量。

3.3 信息甄别机制：价格与数量的选择

在信息甄别模型中，卖家设计的价格和购买数量成为买家类型的信号。卖家通过选择适当的定价和购买方案，迫使买家通过他们的选择透露其类型。例如，通过设置不同的价格、入门费或数量限制，卖家可以强制不同类型的买家做出不同的选择，从而揭示他们的真实类型。

卖家的目标是最大化其利润：

\[\text{max } \sum_{i=1}^{n} \beta_i (T_i - c q_i) \]

其中：

• $ T_i $ 是卖家为类型 $ \theta_i $ 的买家设置的价格，
• $ q_i $ 是类型为 $ \theta_i $ 的买家选择的购买数量，
• $ \beta_i $ 是类型 $ \theta_i $ 买家在市场中的比例，
• $ c $ 是商品的单位成本。

卖家的最优化问题受到参与约束和激励相容约束的限制。卖家通过调整 $ T_i $ 和 $ q_i $，实现信息的甄别，以确保不同类型的买家选择相应的购买行为。

通过整理这些约束，我们可以得到不同类型买家之间的效用差异，并根据这一差异设计价格和数量，从而使得每个买家根据其类型选择相应的购买数量。通过信息甄别机制，卖家可以通过设计价格和数量的组合来迫使买家透露其类型。这种方式避免了逆向选择问题，即高需求类型的买家不会伪装成低需求类型的买家，反之亦然。通过价格和数量的选择，卖家能够实现信息的甄别并最大化自身的利润。

四、健康保险市场中的逆向选择

在健康保险市场中，逆向选择主要发生在投保人和保险公司之间的信息不对称上。具体来说，投保人比保险公司更清楚自己的健康状况。健康状况是离散的，可以粗略地分为两类：健康（低风险）；不健康（高风险）。对于健康的个体来说，他们的预期医疗支出低，但统一的保费过高，因此健康的人更倾向于不购买保险（或者仅选择最低保障）。不健康的个体则知道自己生病的概率高，预期医疗支出大大高于保费，因此他们更倾向于购买保险，甚至购买全面保障。由于高风险的个体占据了市场，保险公司承担的赔付风险增加，迫使其进一步提高保费。保费上升后，更多健康个体退出市场，导致市场上风险个体比例进一步增加，保费再度上涨。这种恶性循环最终可能导致健康人群几乎完全退出保险市场，只有高风险人群留在市场，甚至可能导致市场崩溃。

模型假设

• 投保人可以分为两类：健康个体（低风险）和不健康个体（高风险）。假设健康个体的比例为 \(p_H\)，不健康个体的比例为 \(p_S = 1 - p_H\)。
• 健康个体生病的概率为 \(q_H\)，而不健康个体生病的概率为 \(q_S\)，且 \(q_S > q_H\)。
• 保险公司不知道个体的具体健康状况，只知道群体的平均生病概率，并根据该平均概率定价。

投保人

• 健康个体的预期成本：健康个体如果不购买保险，其预期医疗成本为 \(E_C^H = q_H \cdot L\)，其中 \(L\) 是生病时的医疗费用。
• 不健康个体的预期成本：不健康个体的预期医疗成本为 \(E_C^S = q_S \cdot L\)。

保险公司定价
由于保险公司不知道具体每个投保人的健康状况，因此只能基于平均概率来定价。保险公司的目标是通过保费 \(P\) 覆盖每个投保人预期的医疗成本。因此保费 \(P\) 可以表示为：$$P = p_H \cdot q_H \cdot L + p_S \cdot q_S \cdot L$$ 即保险公司根据健康个体和不健康个体的比例及其各自的生病概率，计算出平均预期医疗成本。

投保人的决策

• 健康个体的投保选择： 健康个体会选择投保当且仅当保费 \(P\) 低于其不投保时的预期医疗支出 \(E_C^H\)。即当以下条件成立时，健康个体会投保：$$P \leq q_H \cdot L$$
• 不健康个体的投保选择： 不健康个体会选择投保当且仅当保费 \(P\) 低于其不投保时的预期医疗支出 \(E_C^S\)。即当以下条件成立时，不健康个体会投保：$$P \leq q_S \cdot L$$

逆向选择的出现
由于 \(q_S > q_H\)，不健康个体的预期医疗支出高于健康个体。如果保险公司根据所有人的平均预期医疗支出设定保费 \(P\)，则该保费通常介于健康和不健康个体的预期成本之间：$$q_H \cdot L < P < q_S \cdot L$$ 这会导致以下结果：

• 健康个体的预期医疗支出低于保费 \(P\)，因此他们可能退出市场。
• 不健康个体的预期医疗支出高于保费 \(P\)，因此他们会选择留在市场并购买保险。

随着健康个体的退出，市场上高风险投保人占据主导地位，保险公司不得不再次提高保费。这种循环会导致越来越多的健康人群退出，最终导致逆向选择。

逆向选择的数学推导

• 首次定价时，假设保险公司预期健康个体和不健康个体均会购买保险，因此设定保费为：$$P_0 = p_H \cdot q_H \cdot L + p_S \cdot q_S \cdot L$$
• 健康个体退出市场：当保费 \(P_0\) 大于健康个体的预期医疗支出时，即当 \(P_0 > q_H \cdot L\)，健康个体会选择不购买保险。$$P_0 > q_H \cdot L$$
• 调整后的定价：健康个体退出后，保险公司面临的只有不健康个体，新的保费 \(P_1\) 将根据不健康个体的预期医疗成本设定：$$P_1 = q_S \cdot L$$
  此时，保费 \(P_1\) 完全基于高风险个体的医疗风险。

解决逆向选择的办法

• 强制保险：政府可以通过强制所有人购买保险来打破逆向选择的恶性循环。通过强制保险，即使健康个体不愿意支付较高的保费，也无法退出市场。这样可以保持市场的平衡。
• 风险分类：保险公司可以通过体检或其他信息获取渠道，对投保人进行风险分类，针对高风险和低风险人群定价。通过风险分类，保险公司可以设定不同的保费，避免统一保费造成健康人群退出的问题。

五、总结

逆向选择有这么几个特征：一是买卖双方信息不对称；二是信息劣势方只愿意支付一个平均价格，即保留价格；三是劣币驱逐良币。在信息充分透明的市场环境中，如果两个商品质量相同，人们会购买价格更低的那个，价格高的那个被淘汰；如果两个商品价格相同，人们会购买质量更高的那个，质量低的那个被淘汰，这是典型的正向选择，所以正向选择的前提假设是信息对称，买方可以分辨出孰优孰劣。然而现实中信息不对称的情况更常见，所以买方很难分辨哪个产品质高、价低，便只能根据理性预期给出“保留价格”，而保留价格的存在自然会导致劣币驱逐良币，最终形成逆向选择。
逆向选择这种行为对市场产生了严重的危害。首先，逆向选择破坏了市场的公平性和透明度。买卖双方的信息不对称导致了信息的不公平分配，使得某一方能够从中获益，而另一方则可能因此遭受损失。这种情况下，市场的运行就无法体现真实的供需关系，阻碍了资源的有效配置。其次，逆向选择削弱了市场的信任。当交易中存在虚假信息时，其他市场参与者会感到不安，因为他们很难判断信息的真实性。这样的情况下，人们可能会更加谨慎，甚至选择退出市场，从而降低了市场的活跃度和流动性。此外，逆向选择还可能导致市场崩溃。如果市场上充斥着虚假信息和劣质产品，消费者的信心将受到严重动摇，从而减少了消费意愿。当消费者不再相信市场中的产品和信息时，市场可能会面临崩溃的风险，造成整体经济损失。逆向选择对市场造成了严重的危害，破坏了市场的公平性、透明度和信任，甚至可能引发市场崩溃。为了解决这一问题，监管机构需要制定严格的法规来防止虚假信息的传播，并加强市场监管，以确保市场的正常运行和健康发展。

参考文献

1. 不完美信息动态博弈--逆向选择与道德风险
2. 浅析经济学中的逆向选择
3. 信息不对称问题（1）逆向选择

Akerloff's (1970) Model

对称信息

考虑一个二手车市场，其质量用 $ q $ 表示，其中 $ q \in U[0, Q] $，且 $ Q \in (1, 2) $。

• 买家将质量为 $ q $ 的车估值为 $ q $，而卖家则估值为 $ \frac{q}{Q} $。
• 由于 $ \frac{q}{Q} < q $，买家对车的估值高于卖家。
• 这使得双方可以以 $ p $ 介于 $ \frac{q}{Q} $ 和 $ q $ 之间的价格交换汽车，从而卖家获得利润，买家获得剩余。

如果质量为 $ q $ 的车以价格 $ p $ 进行交易，买家获得的效用为：

\[u(p, q) = q - p \]

卖家的利润为：

\[\pi(p, q, Q) = p - \frac{q}{Q} \]

假设有足够多的买家，使得所有的交易收益都被卖家获得。

当买家可以完美观察到车的质量 $ q $ 时，他只在以下情况下购买：

\[q - p \geq 0 \text{ or } p = q \]

也就是说，他从这样的交易中获得的效用是正的。

拥有质量为 $ q $ 的车的卖家预期买家会接受这种规则，并设置价格 $ p $ 使其解决：

\[\begin{aligned} & \max_{p \geq 0} p - \frac{q}{Q} \\ & \text{s.t. } p \leq q \end{aligned} \]

其中 $ p \leq q $ 是买家的参与约束（PC）。

卖家的目标函数可以表示为无约束问题：

\[\max_{p \geq 0} p - \frac{p}{Q} \]

对 $ p $ 求一阶导数（FOC）得到：

\[1 - \frac{1}{Q} > 0 \text{ or } \frac{Q - 1}{Q} > 0 \]

由于定义上 $ Q > 1 $，存在一个角解，即卖家将价格 $ p $ 尽可能提高：

\[p^{SI} = q \]

不对称信息

当买家无法观察到车的真实质量 $ q $ 时，他形成一个期望 $ E(q) $。

买家在车的要价 $ p $ 满足下式时接受交易：

\[p = E(q) \]

卖家预期买家会接受这种规则，并设置价格 $ p $ 使其解决：

\[\begin{aligned} & \max_{p \geq 0} p - \frac{q}{Q} \\ & \text{s.t. } p \leq E(q) \end{aligned} \]

其中 $ p \leq E(q) $ 是买家的参与约束（PC）。

由于条件（PC）必须是紧的，$ p = E(q) $，卖家设置的价格。

\[\begin{gathered} p - \frac{q}{Q} = E(q) - \frac{q}{Q} \geq 0 \\ q \leq Q \cdot E(q) \end{gathered} \]

当 $ q $ 服从均匀分布，即 $ q \sim U[0, Q] $ 时，其期望值为：

\[E(q) = \frac{Q - 0}{2} = \frac{Q}{2} \]

然后，$ Q \cdot E(q) = \frac{Q^2}{2} $。

笔记：卖家要保证自己的利润是正的，因此放在市场上的车的质量必须满足 $ q < \frac{Q^2}{2} $

因此，所有质量相对较低的汽车，$ q \leq \frac{Q^2}{2} $，由卖家以价格：

\[p = E(q) = \frac{Q}{2} \]

提供，卖家获得 $ \frac{Q}{2} - \frac{q}{2} $ 的利润，而买家由于 $ p = E(q) $ 获得的期望效用为零。

质量相对较高的汽车，$ q \geq \frac{Q^2}{2} $，卖家不提供，因为卖家向不知情买家能收取的最高价格 $ p = E(q) $ 无法弥补卖家的成本。

这存在问题。买家无法观察 $ q $ 导致好车（“桃子”）市场的不存在，而只有坏车（“柠檬”）存在于市场中。

恶性循环 - 市场消失

一个完全理性的买家会预期卖家的这种定价决策，即卖家认为只提供低质量的汽车 $ p \leq \frac{Q^2}{2} $ 是值得的。

在这种情况下，买家预期只提供质量为 \(q\in (0, \frac{Q^2}{2} )\) 的汽车。

那么，如果 $ q \sim U[0, Q] $，买家可以计算这些提供汽车的预期质量：

\[E\left[q \left| q \leq \frac{Q^2}{2}\right.\right] = \frac{\frac{Q^2}{2} - 0}{2} = \frac{Q^2}{4} \]

因此，买家只会购买价格满足 $ p = \frac{Q^2}{4} $ 的汽车。

然后，卖家会将价格定为 $ p = \frac{Q^2}{4} $，利润为：

\[p - \frac{q}{Q} = \frac{Q^2}{4} - \frac{q}{Q} \]

只有当质量 $ q $ 满足时才是正的：

\[q \leq \frac{Q^3}{4} \]

一个理性的买家现在会更新其预期汽车质量，满足 $ \frac{Q^3}{4} $，这仅产生期望质量为：

\[E\left[q \left| q \leq \frac{Q^3}{4}\right.\right] = \frac{\frac{Q^3}{4} - 0}{2} = \frac{Q^3}{8} \]

卖家提供那些带来正利润的汽车，即质量 $ q $ 满足：

\[p - \frac{q}{Q} = \frac{Q^3}{8} - \frac{q}{Q} \geq 0 \text{ or } q \leq \frac{Q^4}{8} \]

其接近零的界限比 $ \frac{Q^3}{4} $ 更低。

卖家会将提供的汽车集合进一步向质量线的左侧移动，朝向更差的汽车（接近零）。重复足够多次这个论点，我们发现市场“解体”。它只提供质量最差的汽车，即 $ q = 0 $。买家只愿意支付 $ p = 0 $ 的价格，导致所有其他类型的汽车未售出。