统计学(七)——抽样分布定理

抽样分布定理是数理统计中的基本定理之一，它为我们理解随机变量的分布以及后续的参数估计和假设检验奠定了坚实基础。通过这个定理，统计学家能够研究样本统计量（如样本均值、样本方差等）的分布，并根据样本推断总体特征。抽样分布定理特别重要，因为在实际应用中，我们往往无法获取总体数据，只能依赖于有限的样本来推测总体信息，而抽样分布定理为这种推测提供了理论支持。

一、常用的抽样分布

我们称统计量的概率分布为该统计量的抽样分布。抽样分布为整合来自不同总体的样本构建出统计量与统计量的分布。

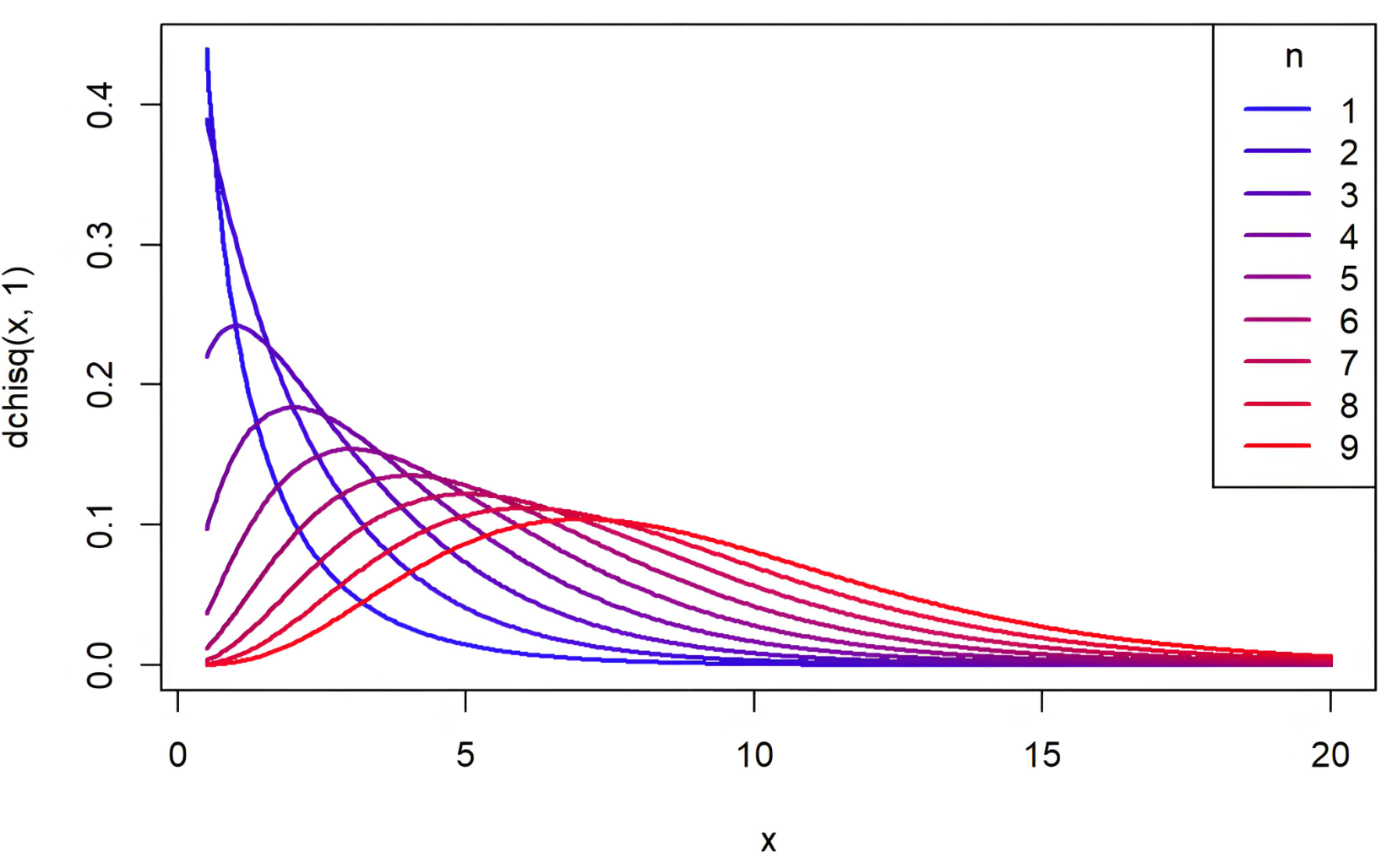
1.1 卡方分布（Chi-square Distribution）

设 $\left(X_1, X_2, \cdots, X_n\right)$ 是来自总体 $N(0,1)$ 的一个样本, 则称统计量

\[\mathrm{Y}=X_1^2+X_2^2+\cdots+X_n^2 \]

是服从自由度为 $n$ 的 $\chi^2$ 分布, 记为 $\mathrm{Y} \sim \chi^2(n)$。$\text {服从} \chi^2 \text {分布的随机变量，经常用 } \chi^2 \text { 来表示 }$
用 $\chi^2$ 表示卡方变量: 称满足

\[P\left\{\chi^2>\chi_\alpha^2(n)\right\}=\int_{\chi_\alpha^2(n)}^{\infty} f(x) d x=\alpha \]

的点 $\chi_\alpha^2(n)$ 为 $\chi^2(n)$ 分布的上侧 $\alpha$ 分位点。

分布图	上侧分位数图

R语言中对应函数：
   ** dchisq(x, df, ncp = 0, log = FALSE)**
   ** pchisq(q, df, ncp = 0, lower.tail = TRUE, log.p = FALSE)**
   ** qchisq(p, df, ncp = 0, lower.tail = TRUE, log.p = FALSE)**
   ** rchisq(n, df, ncp = 0) 其中df即为自由度n。**

1.2 学生t分布（Student t Distribution）

设 $X \sim N(0,1), \quad Y \sim \chi^2(n)$, 且 $X, Y$ 独立, 则称随机变量

\[T=\frac{X}{\sqrt{Y / n}} \]

服从自由度为 $\boldsymbol{n}$ 的 $t$ 分布, 记为 $T \sim t(n)$。
若 $T \sim t(n)$ ，概率密度是 $h(t)$, 则

\[\lim _{n \rightarrow \infty} h(t)=\frac{1}{\sqrt{2 \pi}} e^{-\frac{t^2}{2}} \]

当 $n \rightarrow \infty$ 时, $\mathrm{T}$ 分布的极限分布是标准正态分布，即从大数的意义视角看，$t$分布和正态分布是一样的。对于给定的 $\alpha, 0<\alpha<1$, 称满足条件

\[P\left\{t>t_\alpha(n)\right\}=\int_{t_\alpha(n)}^{+\infty} h(t) d t=\alpha \]

的点 $t_{\boldsymbol{\alpha}}(\boldsymbol{n})$ 为 $t(n)$ 分布的上侧 $\alpha$ 分位点。

分布图	上侧分位数图

R语言中对应函数：
    ** dt(x, df, ncp, log = FALSE)**
    ** pt(q, df, ncp, lower.tail = TRUE, log.p = FALSE)**
    ** qt(p, df, ncp, lower.tail = TRUE, log.p = FALSE)**
    ** rt(n, df, ncp)，其中df即为自由度n。**

1.3 F分布（F Distribution）

设 $X \sim \chi^2\left(n_1\right), Y \sim \chi^2\left(n_2\right)$, 且 $X, Y$ 相互独立, 则称

\[F=\frac{X / n_1}{Y / n_2} \]

服从自由度为 $\left(n_1, n_2\right)$ 的 $F$ 分布, 记为 $F \sim F\left(n_1, n_2\right)$。
对于给定的 $\alpha, 0<\alpha<1$, 称满足条件

\[P\left\{F>F_\alpha\left(n_1, n_2\right)\right\}=\int_{F_\alpha\left(n_1, n_2\right)}^{+\infty} \psi(y) d y=\alpha \]

\[F_{1-\alpha}\left(n_1, n_2\right)=\frac{1}{F_\alpha\left(n_2, n_1\right)} \]

的点 $F_\alpha\left(n_1, n_2\right)$ 为 $F\left(n_1, n_2\right)$ 分布的上侧 $\alpha$ 分位点。

分布图	上侧分位数图

R语言中对应函数：
    ** df(x, df1, df2, ncp, log = FALSE)**
    ** pf(q, df1, df2, ncp, lower.tail = TRUE, log.p = FALSE)**
    ** qf(p, df1, df2, ncp, lower.tail = TRUE, log.p = FALSE)**
    ** rf(n, df1, df2, ncp)，其中df1,df2即为自由度n1,n2。**

二、抽样分布定理

样本均值（Sample Mean）为：$$\bar{X} = \frac{1}{n} \sum_{i=1}^{n} x_i$$
其中：

$ \bar{X} $ 表示样本均值。
$ x_i $ 表示第 $ i $ 个样本值。
$ n $ 表示样本的总数。

样本方差（Sample Variance）为：$$S^2 = \frac{1}{n-1} \sum_{i=1}^{n} (x_i - \bar{X})^2$$
其中：

$ S^2 $ 表示样本方差。
$ x_i $ 表示第 $ i $ 个样本值。
$ \bar{X} $ 表示样本均值。
$ n $ 表示样本的总数。

假设 $X_1,X_2,\dots,X_n$是来自总体$N(\mu,\sigma^2)$的样本，$\bar{X}$和$S^2$分别为样本均值和样本方差，则有：
(1)$\bar{X}\backsim N(\mu,\frac{\sigma^2}{n})$;
(2)$\bar{X}$与$S^2$相互独立;
(3)$\frac{(n-1)S^2}{\sigma^2}\backsim \chi^2(n-1)$

样本均值的期望：

\[\begin{align*} E(\overline{X}) &= E\left(\frac{1}{n} \sum_{i=1}^n X_i\right) \\ &= \frac{1}{n} E\left(\sum_{i=1}^n X_i\right) \\ &= \frac{1}{n} \sum_{i=1}^n E(X_i) \\ &= \frac{1}{n} \times n \times \mu \\ &= \mu \end{align*}\]

样本均值的方差：

\[\begin{align*} D(\overline{X}) &= D\left(\frac{1}{n} \sum_{i=1}^n X_i\right) \\ &= \frac{1}{n^2} D\left(\sum_{i=1}^n X_i\right) \\ &= \frac{1}{n^2} \sum_{i=1}^n D(X_i) \\ &= \frac{1}{n^2} \times n \times \sigma^2 \\ &= \frac{\sigma^2}{n} \end{align*}\]

三、抽样分布的衍生分布

定理1（样本均值分布）

设 $X_1, X_2, \dots, X_n$ 是来自总体$N(\mu,\sigma^2)$的样本，样本均值 $\bar{X}$ 标准化后的分布为标准正态分布N(0,1)。

\[Z = \frac{\bar{X} - \mu}{\sigma / \sqrt{n}} \backsim N(0,1) \]

定理2（样本的均值与方差的联合分布）

设 $X_1,X_2,\dots,X_n$是来自总体$N(\mu,\sigma^2)$的样本，$\bar{X}$和$S^2$分别为样本均值和样本方差，则有

\[\frac{\bar{X}-\mu}{S/\sqrt{n}}\backsim t( n − 1 ) \]

定理3 （两总体样本均值差的分布）

设 $X\backsim N(\mu_1,\sigma^2)$，$ Y \backsim N(\mu_2,\sigma^2)$ ,且$X$与$Y$独立， $X_1,X_2,\dots,X_{n1}$是来自总体$N(\mu_1,\sigma^2)$的样本，$Y_1,Y_2,\dots,Y_{n2}$是来自总体$N(\mu_2,\sigma^2)$的样本，$S_1^2 $ 和 $S_2^2 $ 分别是这两个样本的样本方差，则有

\[\frac{\bar{X} −\bar{Y} − (\mu_1-\mu_2)}{\sqrt{\frac{(n1-1)S_1^2+(n2-1)S_2^2}{n1+n2-2}}\sqrt{\frac{1}{n1}+\frac{1}{n2}}} \backsim t ( n 1 + n 2 − 2 ) \]

定理4 （两总体样本方差比的分布）

设 $X\backsim N(\mu_1,\sigma_1^2)$，$ Y \backsim N(\mu_2,\sigma_2^2)$ ,且$X$与$Y$独立， $X_1,X_2,\dots,X_{n1}$是来自总体$N(\mu_1,\sigma_1^2)$的样本，$Y_1,Y_2,\dots,Y_{n2}$是来自总体$N(\mu_2,\sigma_2^2)$的样本，$S_1^2 $ 和 $S_2^2 $ 分别是这两个样本的样本方差，则有

\[{\frac{S_1^2}{\sigma_1^2}} / {\frac{S_2^2}{\sigma_2^2}} \backsim F(n1 − 1 , n2 −1) \]

定理5 （两总体t分布的相加性）

设 $ X_1, X_2, \cdots, X_m $ 服从正态分布 $\sim N(a_1, \sigma_1^2)$, $ Y_1, Y_2, \cdots, Y_n $ 服从正态分布$\sim N(a_2, \sigma_2^2)$, 且假定 $\sigma_1^2 = \sigma_2^2 = \sigma^2$, 样本 $ X_1, X_2, \cdots, X_m $ 与 $ Y_1, Y_2, \cdots, Y_n $ 独立，则

\[T = \frac{(\bar{X} - \bar{Y}) - (a_1 - a_2)}{S_w} \cdot \sqrt{\frac{mn}{n+m}} \sim t_{n+m-2} \]

此处 $(n+m-2)S_w^2 = (m-1)S_1^2 + (n-1)S_2^2$，其中

\[S_1^2 = \frac{1}{m-1} \sum_{i=1}^{m} (X_i - \bar{X})^2, \quad S_2^2 = \frac{1}{n-1} \sum_{j=1}^{n} (Y_j - \bar{Y})^2. \]

证明： 由抽样分布定理可知 $\bar{X} \sim N(a, \sigma^2/m), \bar{Y} \sim N(a_2, \sigma^2/n)$，故有 $\bar{X} - \bar{Y} \sim N(a_1 - a_2, (\frac{1}{m} + \frac{1}{n})\sigma^2) = N(a_1 - a_2, \frac{m+n}{mn}\sigma^2)$。将其标准化得

\[\frac{\bar{X} - \bar{Y} - (a_1 - a_2)}{\sigma} \sqrt{\frac{mn}{m+n}} \sim N(0, 1). \tag{1} \]

又 $(m-1)S_1^2/\sigma^2 \sim \chi^2_{m-1}, (n-1)S_2^2/\sigma^2 \sim \chi^2_{n-1}$，再利用 $\chi^2$ 分布的性质可知

\[\frac{(m-1)S_1^2 + (n-1)S_2^2}{\sigma^2} \sim \chi^2_{n+m-2}. \tag{2} \]

再由 (1) 和 (2) 中 $(\bar{X}, \bar{Y})$ 与 $(S_1^2, S_2^2)$ 相互独立，由定义可知

\[T = \frac{(\bar{X} - \bar{Y}) - (a_1 - a_2)}{\sigma} \sqrt{\frac{mn}{n+m}} / \sqrt{\frac{(m-1)S_1^2 + (n-1)S_2^2}{\sigma^2(n+m-2)}} \]

\[= \frac{(\bar{X} - \bar{Y}) - (a_1 - a_2)}{S_w} \sqrt{\frac{mn}{n+m}} \sim t_{n+m-2}. \]

总结

抽样分布定理的重要性体现在它为统计学中的推断理论提供了核心支撑。它帮助我们理解在重复抽样中，样本统计量的分布特征，并通过这种理解来构建有效的估计和检验方法。无论是在经济学、社会学、医学研究还是机器学习中，抽样分布定理都扮演着不可或缺的角色，使得基于有限样本对总体进行推断成为可能。掌握这个定理以及相关的数学证明，不仅有助于统计学的学习与应用，还能帮助我们在实际问题中做出更加科学和严谨的判断。

参考文献

posted @ 2022-08-02 19:24 郝hai 阅读(4368) 评论(1) 收藏举报

刷新页面返回顶部

haohai9309

格物致知，知行合一！