中心极限定理的模拟—R实现

中心极限定理（Central Limit Theorem，简称CLT）是概率论和统计学的基石之一。它揭示了一个极其重要的统计学现象：无论原始变量的分布形态如何，当大量独立随机变量的和或均值被标准化后，它们的分布都会趋向于正态分布。换句话说，只要样本量足够大，许多看似无规律的随机现象在总体上都会呈现出正态分布的模式，这也是为什么正态分布在实际统计分析中如此普遍的原因。
这一理论的建立历经两百余年，经历了多个阶段的演化。从1733年法国数学家德·穆阿夫尔（Abraham de Moivre）在研究二项分布时的初步发现，到18世纪末拉普拉斯（Pierre-Simon Laplace）对该理论的推广，再到19世纪切比雪夫（Pafnuty Chebyshev）、**马克洛夫（Andrey Markov）和李雅普诺夫（Aleksandr Lyapunov）的数学推进，最终由保罗·莱维（Paul Lévy）和威廉·费勒（William Feller）**在1937年给出严格的数学证明，中心极限定理才最终成为现代统计学的核心支柱之一。

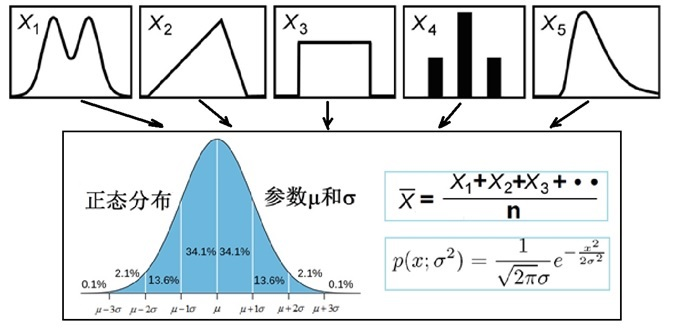
一、统计学理论根基——中心极限定理

中心极限定理有着有趣的历史。这个定理的第一版被法国数学家棣莫弗发现，他在1733年发表的卓越论文中使用正态分布去估计大量抛掷硬币出现正面次数的分布。这个超越时代的成果险些被历史遗忘，所幸著名法国数学家拉普拉斯在1812年发表的巨著Théorie Analytique des Probabilités中拯救了这个默默无名的理论。拉普拉斯扩展了棣莫弗的理论，指出二项分布可用正态分布逼近。但同棣莫弗一样，拉普拉斯的发现在当时并未引起很大反响。直到十九世纪末中心极限定理的重要性才被世人所知。1901年，俄国数学家里雅普诺夫用更普通的随机变量定义中心极限定理并在数学上进行了精确的证明。如今，中心极限定理被认为是(非正式地)概率论中的首席定理。

设随机变量\(X_1\)，\(X_2\)，...，\(X_n\)，...独立同分布，并且具有有限的数学期望和方差：\(E({X_i})=\mu\)，\(D({X_i})\)=\(\sigma^2(i=1，2，...)\)，则对任意\(x\)，分布函数

\[F_n(x)=P\left\{\frac{\sum_{i=1}^n X_i-n \mu}{\sigma \sqrt{n}} \leq x\right\} \]

满足

\[\lim _{n \rightarrow \infty} F_n(x)=\lim _{n \rightarrow \infty} P\left\{\frac{\sum_{i=1}^n X_i-n \mu}{\sqrt{n} \sigma} \leq x\right\}=\frac{1}{\sqrt{2 \pi}} \int_{-\infty}^x e^{-\frac{t^2}{2}} d t=\varnothing(x) \]

该定理说明，当很大时，随机变量

\[Y_n=\frac{\sum_{i=1}^n X_i-n \mu}{\sqrt{n} \sigma} \]

近似地服从标准正态分布N(0，1)。

从定理可知，期望为\(\mu\)，方差为\(\sigma^2\)的独立同分布随机变量序列 \(X_1\),\(X_2\),...,\(X_n\)之和$$\sum\limits_{k=1}^nX_k$$​的标准化变量，当\(n\)足够大时，近似服从标准正态分布，即$$ \frac{\sum\limits_{k=1}^nX_k-n\mu}{\sqrt{n}\sigma}\sim N(0,1) $$

由于

\[\frac{\sum_{\mathrm{k}=1}^{\mathrm{n}} \mathrm{X}_{\mathrm{k}}-\mathrm{n} \mu}{\sqrt{\mathrm{n}} \sigma}=\frac{\frac{1}{\mathrm{n}} \sum_{\mathrm{k}=1}^{\mathrm{n}} \mathrm{X}_{\mathrm{k}}-\mu}{\sigma / \sqrt{\mathrm{n}}}=\frac{\overline{\mathrm{X}}-\mu}{\sigma / \sqrt{\mathrm{n}}} \]

因此有$$ \frac{\overline X-\mu}{\sigma/\sqrt{n}}\sim N(0,1) \quad 或 \quad \overline X \sim N(\mu,\sigma^2/n)$$ 这是独立同分布的中心极限定理结果的另一个形式(Important!!!)。在实际工作中，只要n足够大，便可以把独立同分布的随机变量之和当作正态变量。

二、中心极限定理模拟

中心极限定理告诉我们，当样本量足够大时，样本均值的分布慢慢变成正态分布，如下图：

2.1 指数分布

library(moments)
options(digits = 3)
options(scipen = 200)

X = rexp(10000, rate=1)  # 原始分布，可以随便设置,这里为指数分布
X_mean = mean(X)         # 原始分布的均值
X_var= var(X)            # 原始分布的方差


m=5000 # 抽取的次数
par(new=TRUE)
par(mfrow=c(3,3)) 

for(n in c(1,5,10,20,30,50,100,500,1000))
  {
  # 每次从原始分布里随机抽取样本的个数
  s=c()
  
   for(j in 1:m) 
    {
    sample=sample(X,n)# 从原始分布里随机选取n个样本
    sample_mean = mean(sample)# 求样本的均值
    s[j]=sample_mean
    }
   hist(s,breaks = 50,xlab ="",main = paste('n = ',n,sep=''))
  }

2.2 二项分布

library(moments)
options(digits = 3)
options(scipen = 200)

X = rbinom (10000,size=1,prob =0.7)   # 原始分布，可以随便设置,这里为二项分布
X_mean = mean(X)                      # 原始分布的均值
X_var= var(X)                         # 原始分布的方差


m=1000 # 抽取的次数
par(new=TRUE)
par(mfrow=c(3,3)) 

for(n in c(1,5,10,20,30,50,100,500,1000))
  {
  # 每次从原始分布里随机抽取样本的个数
  s=c()
  
   for(j in 1:m) 
    {
    sample=sample(X,n)# 从原始分布里随机选取n个样本
    sample_mean = mean(sample)# 求样本的均值
    s[j]=sample_mean
    }
   hist(s,breaks = 50,xlab ="",main = paste('n = ',n,sep=''))
  }

2.3 均匀分布

library(moments)
options(digits = 3)
options(scipen = 200)

X = runif(10000, min=0,max = 2)    # 原始分布，可以随便设置,这里为均匀分布
X_mean = mean(X)                      # 原始分布的均值
X_var= var(X)                         # 原始分布的方差


m=5000 # 抽取的次数
par(new=TRUE)
par(mfrow=c(3,3)) 

for(n in c(1,5,10,20,30,50,100,500,1000))
{
  # 每次从原始分布里随机抽取样本的个数
  s=c()
  
  for(j in 1:m) 
  {
    sample=sample(X,n)# 从原始分布里随机选取n个样本
    sample_mean = mean(sample)# 求样本的均值
    s[j]=sample_mean
  }
  hist(s,breaks = 50,xlab ="",main = paste('n = ',n,sep=''))
}

三、总结

中心极限定理的提出和发展是统计学和概率论发展史上的重要里程碑。这一定理不仅在理论上奠定了统计推断的基础，也在现实世界的众多领域中发挥着至关重要的作用。中心极限定理解释了为什么正态分布在实际统计分析中如此普遍，现实世界中的很多现象，比如测量误差、股票价格变动、经济增长率、网络流量、机器学习中的数据分布等，都符合中心极限定理的结论，以下是几个重要应用领域：

• 统计推断：中心极限定理是置信区间和假设检验的理论基础，即使总体分布未知，我们仍然可以用样本均值来近似推断总体均值，并构造统计检验。
• 金融与经济学：在金融市场中，股票收益的变动通常可以近似为正态分布，中心极限定理为此提供了理论支持。此外，许多经济变量（如GDP增长率、通货膨胀率等）可以通过中心极限定理进行建模和分析。
• 数据科学与机器学习：许多机器学习算法（如线性回归、神经网络）依赖于数据的正态性假设，而中心极限定理使得这一假设在大样本情况下可以近似成立。
• 工程与物理科学：在信号处理、测量误差分析、质量控制等领域，许多数据的累积效应可以用中心极限定理来解释。例如，通信信号中的噪声通常服从正态分布，这使得许多滤波和检测方法都基于正态分布模型。

从18世纪的经验观察到20世纪的严格数学证明，中心极限定理经历了两百多年的演进，最终奠定了现代统计学的理论框架。它的广泛适用性和强大解释力，使其成为统计学、经济学、机器学习、工程学等多个领域的重要理论支柱。正如统计学家George E.P. Box 所言：

“统计学的所有理论都建立在中心极限定理之上。”
这一定理不仅是数学理论的核心，更是现实世界数据分析和推断的基石。

参考文献

1. R语言绘图：直方图——hist
2. R 语言与中心极限定理