图与网络分析(三)——最小树问题R和Python实现
最小生成树问题是图论中的经典优化问题,广泛应用于网络设计、交通规划、通信布线等领域。它的目标是在一个连通无向图中,选出一棵覆盖所有顶点的生成树,使得所选边的总权值最小。最小生成树不仅保证了图的连通性,还能有效降低构建成本,具有重要的现实意义。常见的求解算法包括Prim算法、Kruskal算法和Borůvka算法等,它们多采用贪心策略,在每一步选择当前最优边,逐步构建出一棵最优的生成树结构。
一、 最小生成树问题
树:树图是一个无回路且连通的无向图。它包含\(n\)个顶点和\(n-1\)条边,任意两个顶点之间有且仅有一条简单路径。
生成树:一个连通图的生成树是指一个连通子图,它含有图中全部\(n\)个顶点,但只有足以构成一棵树的\(n-1\)条边。一颗有\(n\)个顶点的生成树有且仅有\(n-1\)条边,如果生成树中再添加一条边,则必定成环。
最小生成树:在连通网的所有生成树中,所有边的权数和最小的生成树,称为最小生成树。
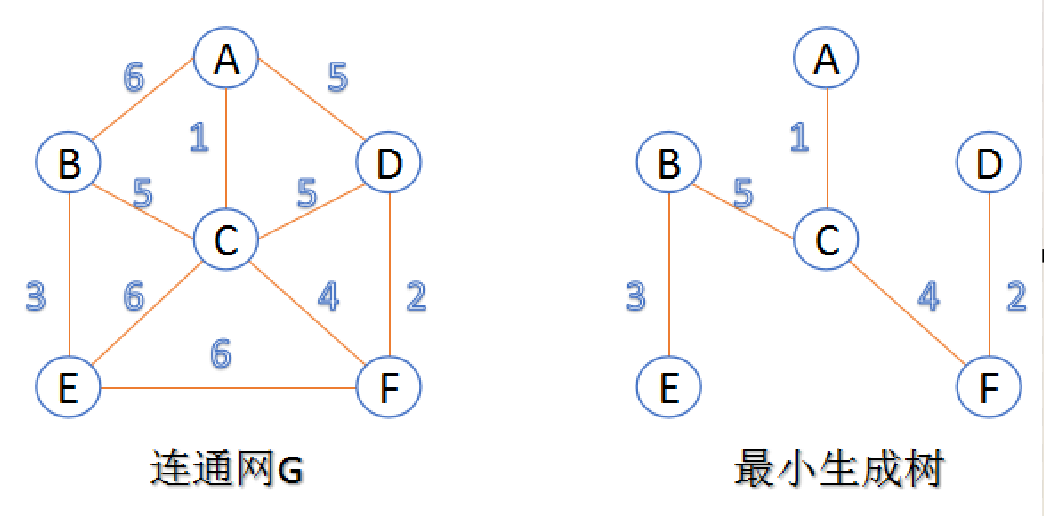
二、 最小生成树算法
2.1 Kruskal算法
此算法可以称为“加边法”,初始最小生成树边数为0,每迭代一次就选择一条满足条件的最小代价边,加入到最小生成树的边集合里。
- 把图中的所有边按权值从小到大排序;
- 把图中的\(n\)个顶点看成独立的\(n\)棵树组成的森林;
- 按权值从小到大选择边,所选的边连接的两个顶点\(u_i,v_i\),应属于两颗不同的树,则成为最小生成树的一条边,并将这两颗树合并作为一颗树。
- 重复(3),直到所有顶点都在一颗树内或者有\(n-1\)条边为止。

2.2 Prim算法
此算法可以称为“加点法”,每次迭代选择代价最小的边对应的点,加入到最小生成树中。算法从某一个顶点\(s\)开始,逐渐长大覆盖整个连通网的所有顶点。
图的所有顶点集合为V;初始令集合u={s},v=V−u;
在两个集合u,v能够组成的边中,选择一条代价最小的边\((u_0,v_0)\),加入到最小生成树中,并把\(u_0v_0\)并入到集合u中。
重复上述步骤,直到最小生成树有\(n-1\)条边或者\(n\)个顶点为止。

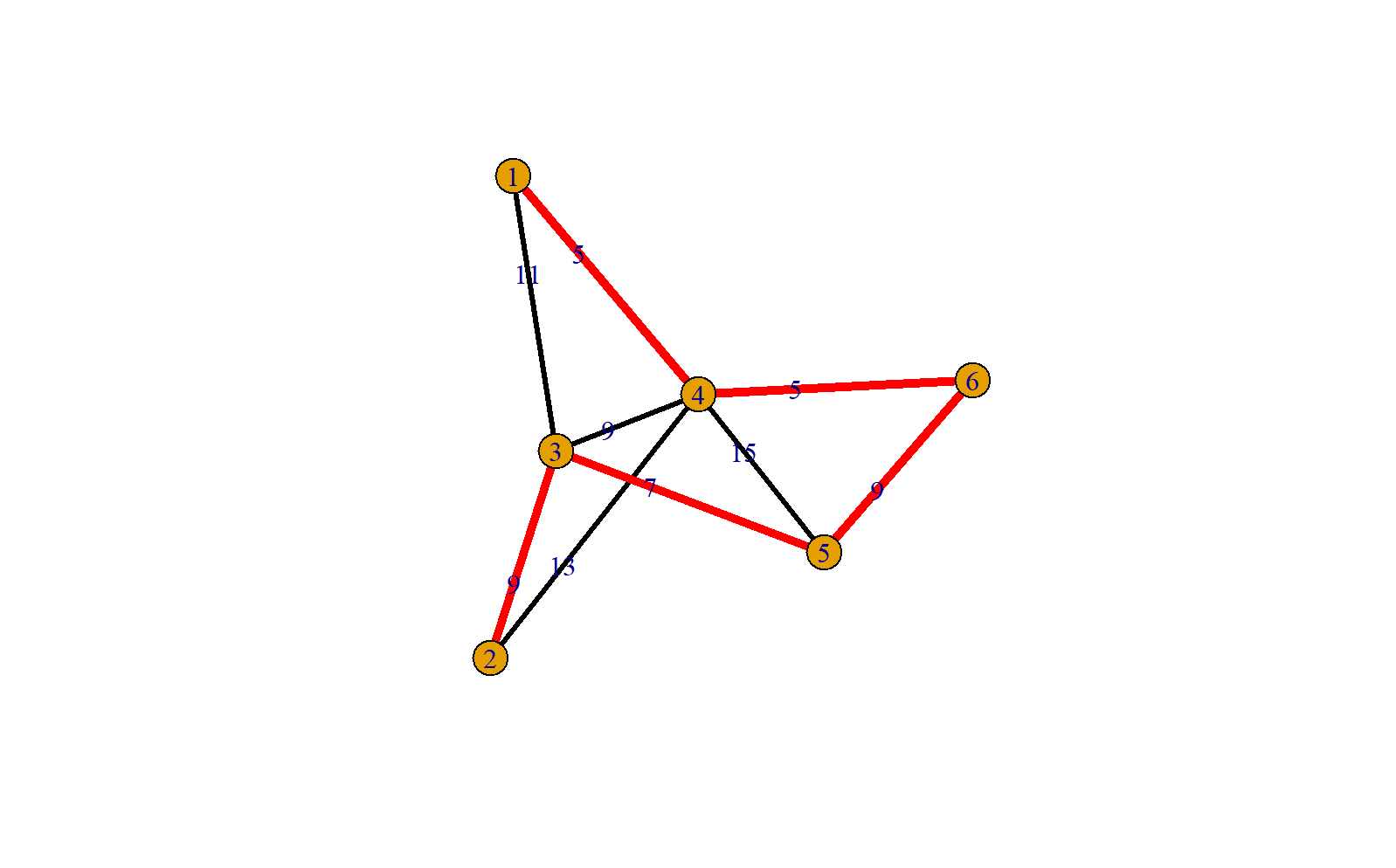
三、 最小生成树R程序
library("igraph")
#赋权图的构建
A = matrix(c(0, 0, 11, 5, 0, 0,0, 0, 9, 13, 0, 0,11, 9, 0, 9, 7, 0,5, 13, 9, 0, 15, 5,0, 0, 7, 15, 0, 9,0, 0, 0, 5, 9, 0),
nrow= 6 , ncol= 6 ,byrow = TRUE)
g<- graph.adjacency(A,weighted=TRUE, mode = c("undirected"))

#最小生成树的计算
tr= minimum.spanning.tree(g,weights = graph_attr(g,'weight'))
plot(tr,layout=layout.reingold.tilford,edge.label=E(tr)$weight)

#最小树合成图
library(dplyr)
ggg=get.data.frame(g)
tr1=get.data.frame(tr)
dd1=setdiff(ggg,tr1)
dd1$color="black"
dd1$width=3
tr1$color="red"
tr1$width=5
ee=union_all(dd1,tr1)
g <- make_graph(t(ee[,1:2]),directed = FALSE)
plot(g,edge.label = ee$weight,edge.color = ee$color,edge.width=ee$width)
四、最小生成树Pyhton程序
给定一个\(n\)阶简单的赋权图G,它的权函数 \(w\) 就决定了一个权矩阵 \(\left[w_{i j}\right]_{n \times n}\) ,其中 \(w_{i i}=\infty, i=1,2, \ldots, n\) ;若 \(v_i v_j \in E(G)\) ,则 \(w_{i j}=w\left(v_i v_j\right)\) ;若 \(v_i v_j \notin E(G)\) ,则 \(w_{i j}=\infty\) 。
可用权矩阵法计算最小树:
- Step0: 划掉矩阵 \(\left[w_{i j}\right]_{n \times n}\) 的第一列(即把第一列的所有元素都改为\(\times\)),并把第 1 行中剩下的每个元素画下划线。
- Step1: 在有下划线的元素中找一个最小的元素 \(w_{k i}\) 。若 \(w_{k i}=\infty\) ,停止,G中不存在支撑树; 否则,把 \(w_{k i}\) 圈起来,然后把第 \(i\) 列其他元素都改为 \(\times\) ,并把第 \(i\) 行没有划掉的元素画下划线。
- Step2: 若所有的元素或者被圈起来或者被划掉,则结束,圈起来的元素对应于最小树的边;否则转Step1。
求 \(G\) 的最小树的过程如下:

import sys
import networkx as nx
import matplotlib.pyplot as plt
# Number of vertices in the graph
V = 5
# Function to find the vertex with the minimum key value, from
# the set of vertices not yet included in the MST
def minKey(key, mstSet):
min = sys.maxsize
min_index = -1
# Search for the vertex not in mstSet that has the smallest key
for v in range(V):
if key[v] < min and not mstSet[v]:
min = key[v]
min_index = v
return min_index
# Function to construct and print MST using adjacency matrix representation
def primMST(graph):
# Array to store the constructed MST
parent = [None] * V
# Key values used to pick the minimum weight edge in cut
key = [sys.maxsize] * V
# To represent the set of vertices included in MST
mstSet = [False] * V
# Always include the first vertex in MST
key[0] = 0
parent[0] = -1 # First node is always the root of the MST
for _ in range(V):
# Pick the minimum key vertex from the set of vertices not yet included in MST
u = minKey(key, mstSet)
# Add the picked vertex to the MST set
mstSet[u] = True
# Update the key value and parent index of the adjacent vertices of the picked vertex
for v in range(V):
# Update the key only if graph[u][v] is smaller than key[v]
if graph[u][v] != float('inf') and not mstSet[v] and graph[u][v] < key[v]:
key[v] = graph[u][v]
parent[v] = u
# Collect the edges of the MST
mst_edges = []
for i in range(1, V):
mst_edges.append((parent[i], i, graph[i][parent[i]]))
return mst_edges
# Adjacency matrix representation of the graph
graph = [
[float('inf'), 50, 30, 40, 25],
[50, float('inf'), 15, 20, float('inf')],
[30, 15, float('inf'), 10, 20],
[40, 20, 10, float('inf'), 10],
[25, float('inf'), 20, 10, float('inf')]
]
# Get the edges of the MST
mst_edges = primMST(graph)
# Create a graph using networkx
G = nx.Graph()
# Add edges to the graph
for i in range(V):
for j in range(V):
if graph[i][j] != float('inf'):
G.add_edge(i, j, weight=graph[i][j])
# Define positions of nodes, adjusting node 0 upwards
pos = nx.spring_layout(G)
pos[0][1] += 0.2 # Move node 0 upwards by 0.2 units
edge_labels = nx.get_edge_attributes(G, 'weight')
plt.figure(figsize=(12, 6))
# Draw the original graph
plt.subplot(121)
nx.draw(G, pos, with_labels=True, node_color='lightblue', node_size=700, font_size=10, font_weight='bold')
nx.draw_networkx_edge_labels(G, pos, edge_labels=edge_labels)
plt.title('Original Graph')
# Create MST graph
MST = nx.Graph()
MST.add_weighted_edges_from(mst_edges)
# Draw the MST graph
plt.subplot(122)
nx.draw(MST, pos, with_labels=True, node_color='lightgreen', node_size=700, font_size=10, font_weight='bold')
nx.draw_networkx_edge_labels(MST, pos, edge_labels={(u, v): d for u, v, d in mst_edges})
plt.title('Minimum Spanning Tree (MST)')
plt.show()
五、最小生成树问题的应用
在实际工程与生活中,许多问题可以抽象为图论中的最小生成树问题。设有一个通信网络\(𝐺\),用于表示\(𝑛\)个城市之间的通信线路连接情况。其中,每个顶点代表一座城市,每条边表示两座城市之间的通信线路,边的权值则表示线路的长度、造价或其他建设成本。在这样的图结构中,寻找一棵连接所有城市、且总权值最小的生成树,就能得到构建通信网络的最优方案。该方案不仅能确保所有城市互相连通,还能使通信线路的总造价最小,从而大大降低建设成本。
这种最小生成树的思想可以广泛应用于各类基础设施优化问题。例如:(1)矿井通风管道设计问题中,需要在复杂的矿井通道中布置通风管道,使得空气能够覆盖所有工作面,并尽可能减少管道的总长度,从而降低施工和材料成本;(2)城市道路规划问题中,几个城市之间修建公路,要求在保证任意城市可达的前提下,使得所建道路总长度最短,以节约资源和提升效率;(3)在城市基础设施设计中,如供水系统、煤气管网、供电线路等的布局,也常常借助最小生成树模型,规划出一条最短路径网络,实现对所有用户的全面覆盖并降低维护成本。

参考文献
[最小生成树的两种方法(Kruskal算法和Prim算法)](https://blog.csdn.net/a2392008643/article/details/81781766/)



 浙公网安备 33010602011771号
浙公网安备 33010602011771号