激活函数之线性整流单元ReLU

线性整流单元(Rectified Linear Unit，ReLU) 是深度学习中最广泛使用的激活函数之一。它因其简单、高效的特性，成为大多数现代神经网络（特别是卷积神经网络 CNN）隐藏层的默认选择。

1. 原理与定义

ReLU 激活函数的作用是给神经网络引入非线性，使其能够学习和逼近复杂的数据模式。

其数学表达式非常简单：𝑓(𝑥)=max(0,𝑥)

这意味着：

• 如果输入值𝑥大于 0，输出就是输入值本身 ( 𝑓(𝑥)=𝑥 )。
  
• 如果输入值𝑥小于或等于 0，输出就是 0 ( 𝑓(𝑥)=0 )。
  

2. 主要特点与优势

ReLU 之所以被广泛采用，主要得益于以下几个显著优势：

• 计算高效： 相比于 Sigmoid 或 Tanh 函数涉及复杂的指数运算，ReLU 只需要进行简单的阈值判断（取最大值），计算速度非常快，有助于加速训练和推理过程。
• 解决梯度消失问题： 对于正数输入 (𝑥>0)，ReLU 的导数恒定为 1。这确保了在反向传播过程中，梯度可以有效地流动到网络的更深层，从而缓解了深层网络中常见的梯度消失问题。
• 引入稀疏性： 由于负值输入会被直接置为 0，网络中的部分神经元处于非激活状态。这种稀疏激活（Sparse Activation）有助于生成稀疏表示，减少计算量，并且具有正则化的效果，有助于防止过拟合。
  

3. 缺点与改进

尽管 ReLU 优点突出，但也存在一个主要的缺点：

• 「死亡 ReLU」问题 (Dying ReLU)： 如果一个神经元在训练过程中持续接收到负输入，那么它的输出将永远是 0，导致反向传播时梯度也永远是 0。这个神经元将永远无法被激活，即「死亡」了。
  

为了解决这个问题，研究人员提出了多种 ReLU 的变体，例如：

• Leaky ReLU： 允许负值输入有一个非常小的非零斜率（例如 0.01x），而不是直接归零，从而避免神经元彻底死亡。

• PReLU (Parametric ReLU)： 将 Leaky ReLU 中的固定斜率 0.01 变成一个可学习的参数𝛼。
• ELU 等其他现代激活函数也在不断发展中。

 

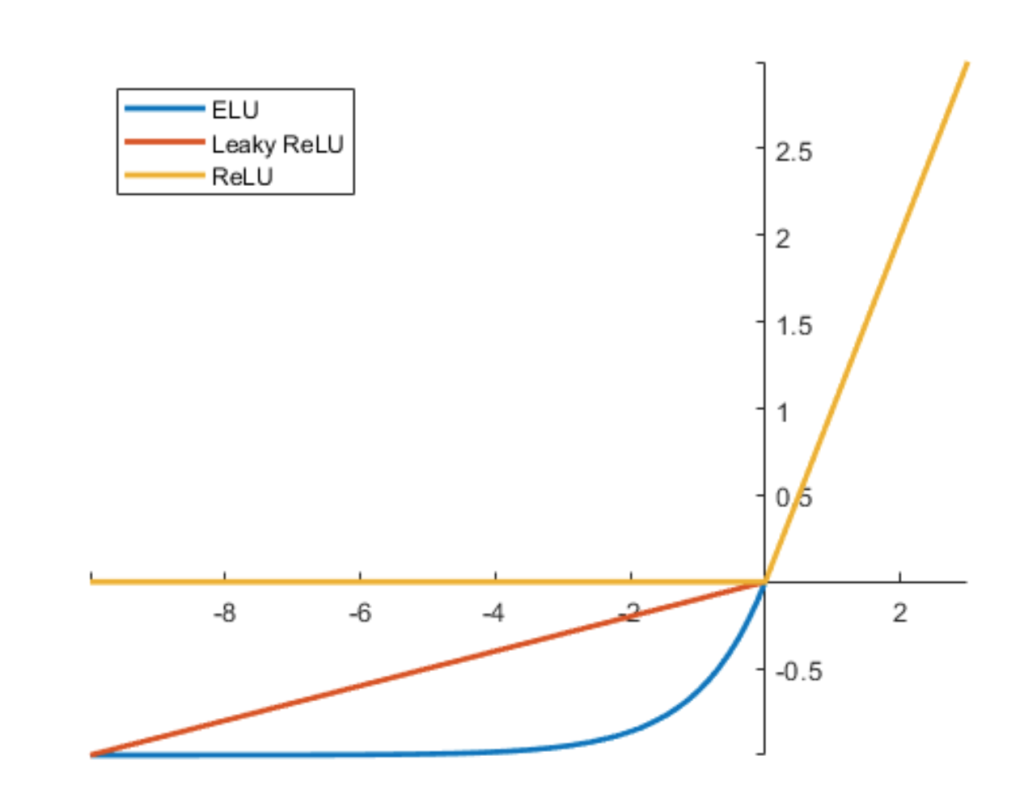
 图1-ReLU,leaky ReLU,ELU图形

总体而言，ReLU 凭借其卓越的性能和计算效率，是目前深度学习模型隐藏层激活函数的首选。 通过图一可以看出，这些函数都是半线性激活函数。还有Softplus.