激活函数之Sigmoid

Sigmoid 激活函数，也称为逻辑函数（Logistic Function），是人工神经网络历史上一个非常重要的激活函数。它因其独特的“S”形曲线而得名，能够将任何实数值输入压缩到一个介于 0 和 1 之间的范围。

1. 数学表达式

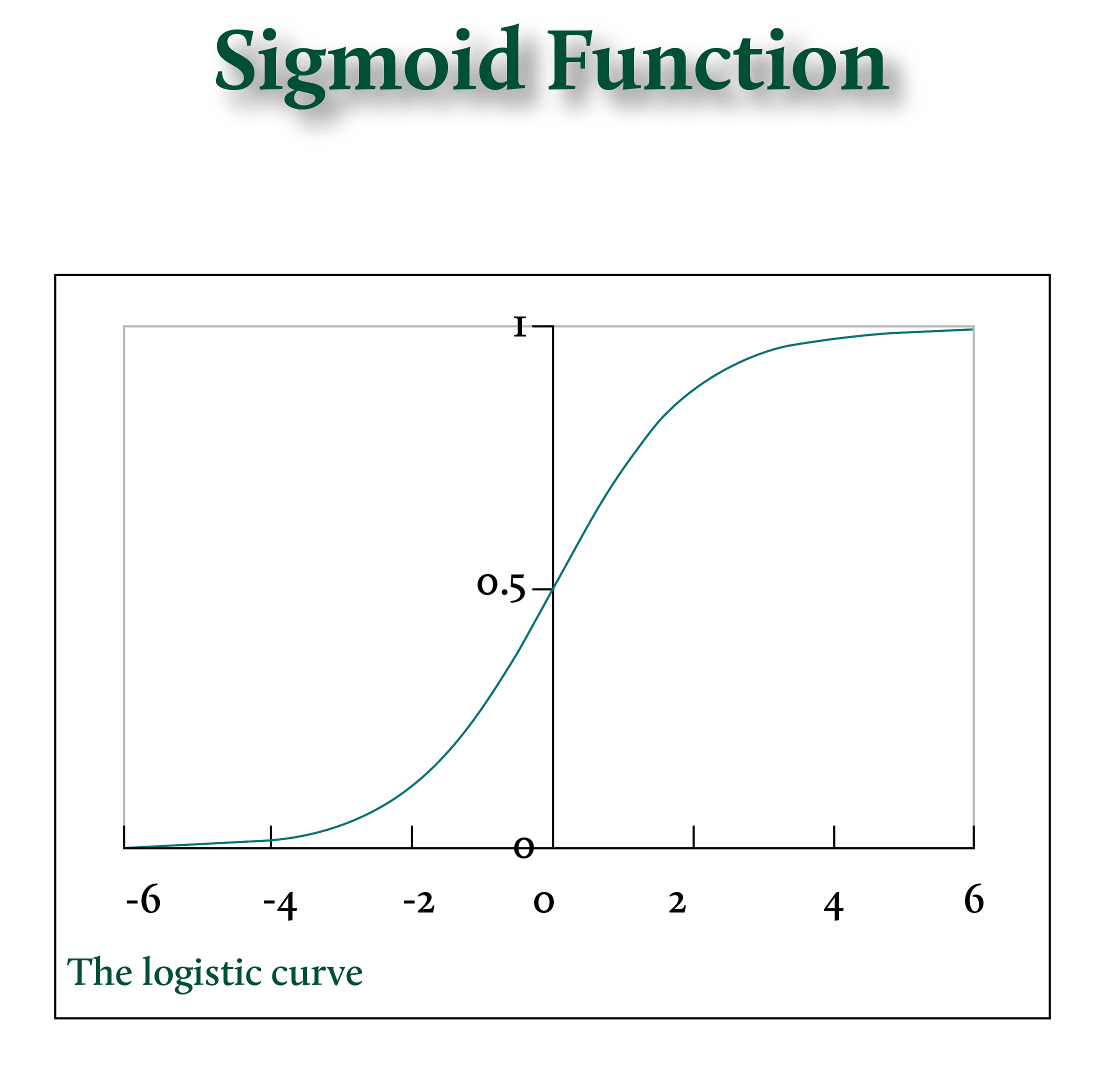
Sigmoid 函数的数学公式如下：𝜎(𝑥)=1 / ( 1 + 𝑒^−𝑥 )

其中，𝑒是自然对数的底数（约等于 2.71828），x是神经元的加权输入总和。

2. 关键特性

• 输出范围 (0, 1)：这是 Sigmoid 最显著的特点。无论输入𝑥是多大或多小（从负无穷大到正无穷大），输出值始终落在 0 到 1 之间。
• 非线性：Sigmoid 是一个非线性函数，使得神经网络能够学习和逼近复杂的非线性决策边界。
• 平滑连续、可微：该函数处处可导，具有平滑的梯度。这对于基于梯度的优化算法（如反向传播）至关重要，因为它允许平稳地计算和更新权重。
• 单调递增：函数值随着输入值的增大而增大。
  

优点

• 概率解释：由于输出范围在 0 到 1 之间，Sigmoid 函数的输出可以被自然地解释为概率。这使得它非常适合用于二元分类问题的输出层。
• 归一化：它可以将具有不同尺度或范围的原始输入值“挤压”到一个标准化的范围内。
  

缺点 (导致其在深层网络中被 ReLU 取代的主要原因)

• 梯度消失问题 (Vanishing Gradient Problem)：当输入值
  
  𝑥非常大（接近 1）或非常小（接近 0）时，Sigmoid 函数的曲线变得非常平坦，即导数（梯度）接近于零。在深层网络中进行反向传播时，这些接近零的梯度在逐层传递过程中会不断相乘，导致前几层的梯度极其微小，使得网络权重无法有效更新，学习过程停滞。
• 输出非零中心化：Sigmoid 的输出值都在 0 以上。这会导致在训练过程中，权重更新的效率降低，使得模型收敛速度变慢。
• 指数运算耗时：Sigmoid 函数涉及指数运算，计算成本相对较高。
  

3. 应用场景

• 二元分类输出层：Sigmoid 函数最主要的现代用途是在处理二元分类任务时，作为输出层的激活函数，用于输出样本属于正向类别的概率。
• 循环神经网络 (RNN/LSTM) 的门控机制：在 LSTM 等网络结构中，Sigmoid 函数常被用作“门”（如遗忘门、输入门）的激活函数，用于控制信息的流动（决定哪些信息应该保留，哪些应该忘记），因为它能提供一个 0 到 1 之间的权重或概率值。
  

在大多数现代深度神经网络的隐藏层中，Sigmoid 函数已经被 ReLU（Rectified Linear Unit）或其变体（如 Leaky ReLU、ELU）所取代，以解决梯度消失问题并加速训练，但 Sigmoid 仍然是二分类问题输出层的标准选择，即在输出层，作为分类函数。

 附言：

不论你叫狗蛋还是毛蛋儿，都是对你的叫法，对于Logistic Function的翻译，这里总结一下，以飨读者分清概念，不至于颠三倒四。

在大多数情况下，尤其是在涉及计算机科学和机器学习的讨论中：

推荐使用“逻辑函数”，因为它更为通用和大众所知。

如果你在进行严格的统计学分析或强调其数学背景，使用“对数几率函数”也是准确的。