电路基础：戴维南定理、诺顿定理

目录

• 戴维南定理
  • 概念
  • 示例
• 诺顿定理
  • 概念
  • 例题
• 参考

戴维南定理

概念

对于一个复杂电路，如下图，如果仅利用基尔霍夫定律，关注电路环、节点，不仅很麻烦，列出大量方程求解，可能有时还无法得出解.

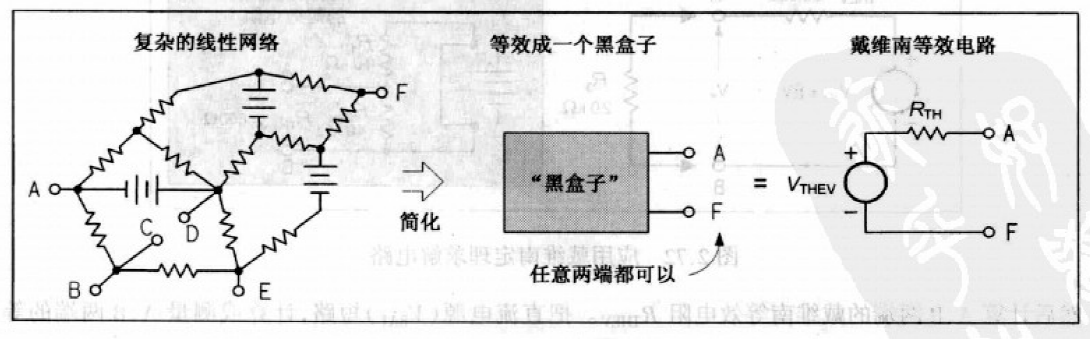
from 参考文献[1]

戴维南提出一种简单方法：
仅关注电路中2个端子之间所连支路的量值，先将端子间这条支路从电路断开，剩余部分看成一个伸出2端子的“黑盒子”，该“黑盒子”，或称线性两端直流网络，可用一个 电压源 + 电阻 串联支路替换.

这个方法，就称为戴维南定理.

适用于复杂二端网络.

串联支路中，电压源叫戴维南等效电压\(V_{THEV}\)，电阻叫戴维南等效电阻\(R_{THEV}\)，整个串联支路叫戴维南等效电路.

该等效电路，再应用欧姆定律， 容易算出与等效电路相连的负载电流：

\[I=V_{THEV}/(R_{THEV}+R_{LOAD}) \]

其中，\(R_{LOAD}\)是端子间负载电阻.

注意：“黑盒子”并不真实存在，而是一个等效电路（即戴维南等效电路）.

要分析复杂电路上的负载电流、电压，就要先去掉负载电阻形成两端电路，然后求戴维南电路等效电路；再将负载电阻与戴维南电路连接，应用欧姆定律，求出负载电流.

戴维南等效电压\(V_{THEV}\)，等效电阻\(R_{THEV}\)物理意义是什么？如何求出？

\(V_{THEV}\)是黑盒子两端电压，可测量或计算得到.

\(R_{THEV}\)是把黑盒子中所有直流电源置0（电压源短路，电流源开路）后，端子间等效电阻，也可以测量或计算得到.

戴维南等效方法本质是叠加原理.

戴维南定理，是应用叠加原理，一次将所有直流电源置0，求出戴维南等效电阻；而叠加原理是每次将一个电源置0，计算部分电流，然后叠加到一起，进而求出戴维南电阻.

示例

例：如下图，如何求出负载电阻\(R_3\)的电压、电流？

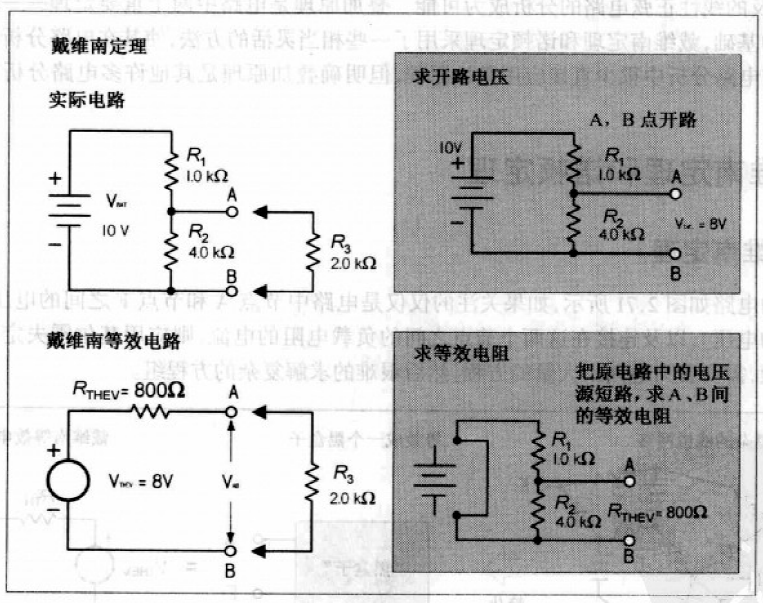
应用戴维南定理，步骤：

1. 计算A、B两端的戴维南等效电压\(V_{THEV}\)

将负载电阻\(R_3\)断开，即A、B端断开，然后求出黑盒子两端A、B电压，即\(V_{THEV}\)（如右上图）：
\(V_{AB}\)是\(R_2\)的两端电压，应用分压公式，

\[V_{THEV}=V_{AB}=\frac{R_2}{R_1+R_2}V_{BAT}=\frac{40}{10+40}10V=8V \]

2. 计算A、B两端的戴维南等效电阻\(R_{THEV}\)

将黑盒子直流电源置0（电压源短路，电流源开路），A、B两端电阻是\(R_1,R_2\)的并联等效电阻（如右下图）

\[R_{THEV}=\frac{R_1R_2}{R_1+R_2}=800Ω \]

注意：分析戴维南电路时，尚未将负载电阻\(R_3\)与黑盒子接上

3. 计算负载电阻上的电压、电流

应用A、B两端的戴维南等效电压、等效电阻求解（如左下图），此时将负载电阻\(R_3\)接入电路，\(R_3\)与等效电阻串联

\[\begin{aligned} V_3 &= \frac{R_3}{R_{THEV}+R_3}V_{THEV}=\frac{2000}{800+2000}8V=5.7V\\ I_3 &= \frac{V_{THEV}}{R_{THEV}+R_3}=\frac{8}{2800}A=0.003A \end{aligned} \]

诺顿定理

概念

类似于戴维南定理，诺顿定理也是用一个复杂的二端网络用一个简单的等效电路替代.

不同点：诺顿等效电路，由一个 电流源 + 电阻 并联而成.
戴维南等效电路，有一个 电压源 + 电阻 串联而成.

诺顿等效电路的 等效电阻 = 戴维南等效电路的电阻

∴ 需要额外计算出等效电流，这个电流称为 诺顿等效电流\(I_{NORTON}\)

诺顿等效电路与戴维南等效电路 可相互转换，本质都是叠加原理.

以上面戴维南定理的例题为例，

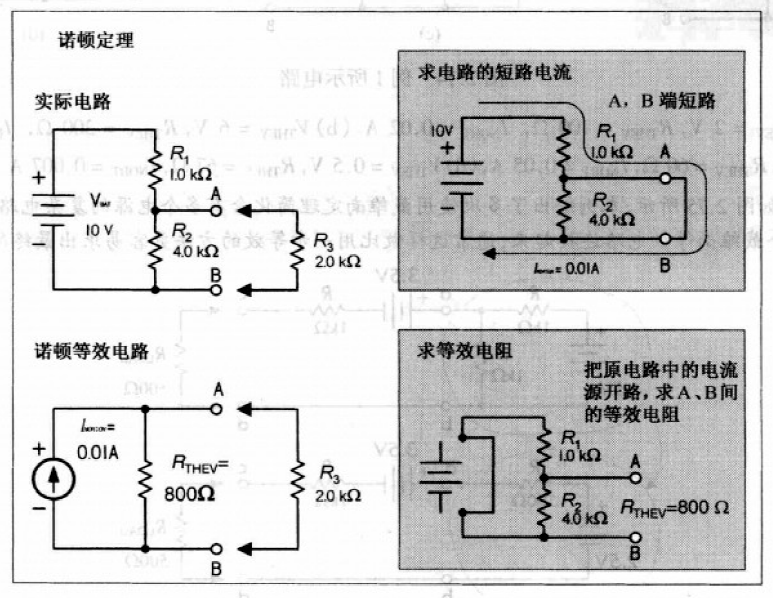
1. 计算诺顿等效电流\(I_{NORTON}\)

去掉负载电阻\(R_3\)，将A、B两端短接，那么\(R_2\)被短路. 应用欧姆定律，

\[I_{NORTON}=\frac{V_{AB}}{R_1}=\frac{10}{1000}A=0.01A \]

2. 计算诺顿等效电阻\(R_{NORTON}\)，同戴维南等效电阻

如右下图，诺顿等效电阻是\(R_1,R_2\)并联的等效电阻

\[R_{NORTON}=800Ω \]

3. 计算负载电流、负载电压

如左下图，将负载\(R_3\)接入，与诺顿等效电阻并联，

\[\begin{aligned} I_3 &= \frac{R_{THEV}}{R_{THEV}+R_3}I_{NORTON}=\frac{800}{800+2000}0.01A=0.003A\\ V_3 &= I_{THEV}\frac{R_{THEV}R_3}{R_{THEV}+R_3}=5.7V \end{aligned} \]

可以发现，跟应用戴维南定理得到结果一样.

例题

例1，求出下面4个电路中，A、B点之间的戴维南等效电压、等效电阻，诺顿等效电流

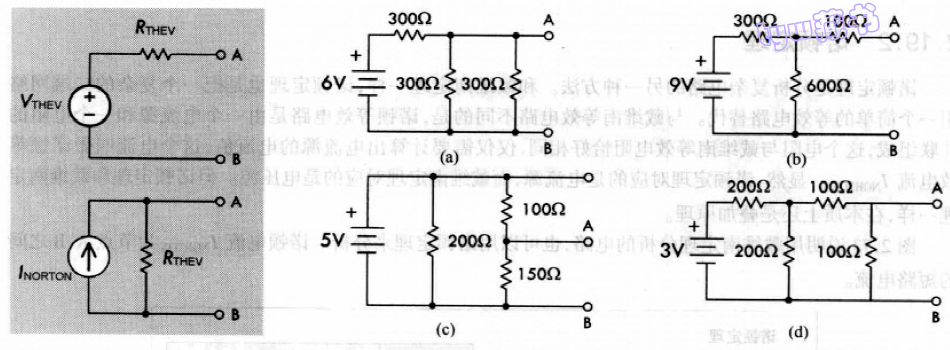
注意：
求戴维南等效电压时，需要先断开负载；
求A、B两端戴维南等效电阻，是在原电路基础上，将电压源置0（短路）；
求诺顿等效电流时，需要断开负载，然后短接A、B；

a）\(V_{THEV}=2V, R_{THEV}=100Ω, I_{NORT}=0.02A\)
计算R时，需要短接电压源，等效电压作为A、B端电压

b）\(V_{THEV}=6V, R_{THEV}=300Ω, I_{NORT}=0.02A\)

c）\(V_{THEV}=3V, R_{THEV}=60Ω, I_{NORT}=0.05A\)
计算R时，等效电阻：电压源短路，100Ω与150Ω电阻并联
计算\(I_{NORT}\)时，150Ω被短路；

d）\(V_{THEV}=0.5V, R_{THEV}= 66.7Ω, I_{NORT}=0.0075A\)

参考

[1]美 舍茨 Scherz, Paul.实用电子元器件与电路基础[M].电子工业出版社,2009.