电路基础：基尔霍夫定律

目录

• 基尔霍夫定律
  • 基尔霍夫电压定律
  • 基尔霍夫电流定律
• 参考

基尔霍夫定律

基尔霍夫电压定律

基尔霍夫电压定律（回路定律）：电路中沿任一回路的所有电压的代数和为0：

\[\sum_{close \ path}\Delta V = V_1+V_2+...+V_N \]

本质：能量守恒定律
<=> 一个电荷从电路任一点出发，沿任一回路绕行一周回到出发点，电荷电势变化量为0

可应用于任何含有线性或非线性元件的电路，包括含电阻、电感、电容、非线性二极管、正弦电压源的电路.

基尔霍夫电流定律

基尔霍夫电流定律（节点定律）：流入一个节点的所有电流之和等于流出该节点的所有电流之和：

\[\sum I_{in}=\sum I_{out} \]

本质：电荷守恒定律
<=> 流过电路的电荷，绝不会凭空产生、消失

• 例题

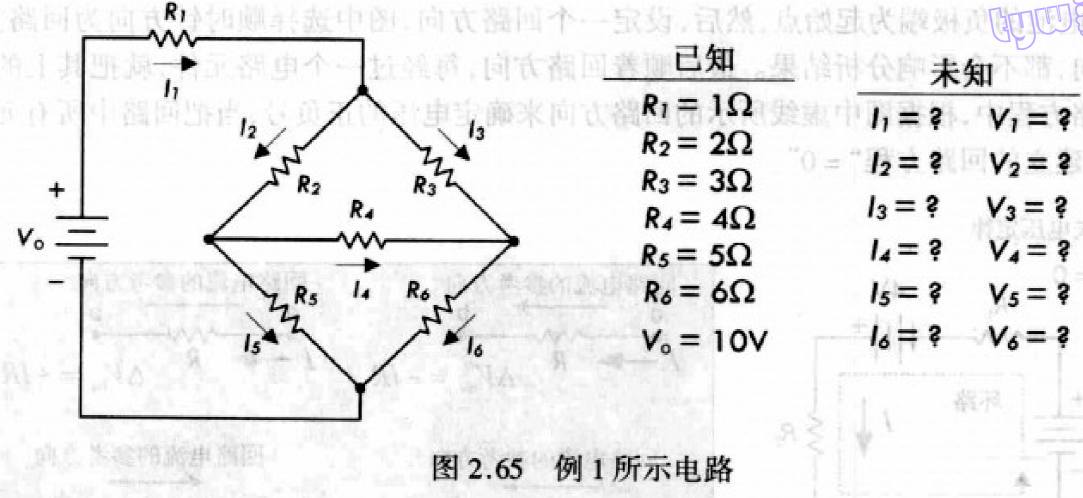
如下图电路，已知电阻\(R_1,R_2,R_3,R_4,R_5,R_6\)、电源电压\(V_o\). 应用基尔霍夫电流定律求流过各电阻电流：\(I_1,I_2,I_3,I_4,I_5,I_6\)，并应用欧姆定律：\(V_n=I_nR_n\)，求各电阻上的电压\(V_1,V_2,V_3,V_4,V_5,V_6\).

解：基尔霍夫电压定律需要找回路，电流定律需要找节点. 然后，建立 方程数 = 未知数数量的 方程组

如下图，分别找3个回路、3个节点，建立方程组：

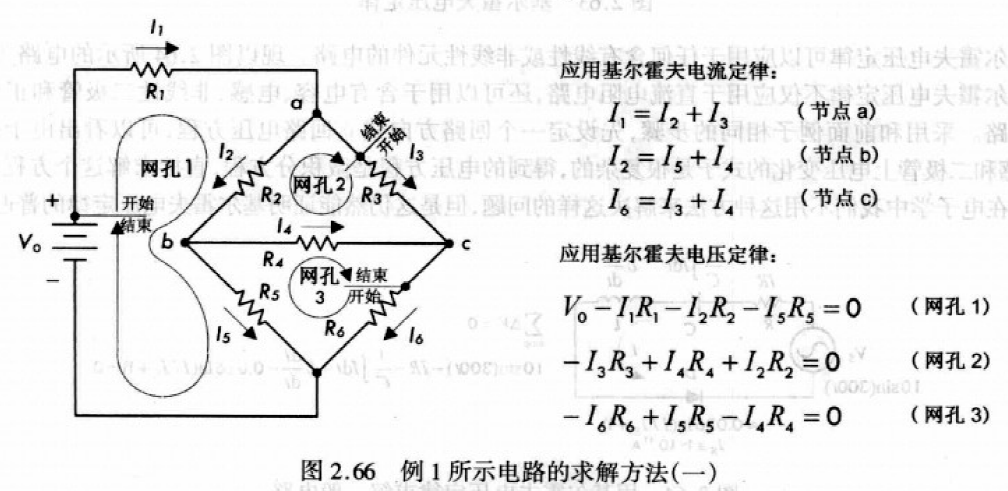
可以解出：

\[V_1=2.027V, I_1=2.027A\\ V_2=2.351V, I_1=1.175A\\ V_3=2.555V, I_1=0.852A\\ V_1=0.204V, I_1=0.051A\\ V_1=5.622V, I_1=1.124A\\ V_1=5.417V, I_1=0.903A\\ \]

手算这个方程组很麻烦，可以用行列式来求解. 行列式可以用LU分解，或\(A^{-1}=A*/|A|\)结合计算机快速求解.

方程组：

\[\begin{aligned} I_1 - I_2 - I_3 &= 0\\ I_2 - I_4 - I_5 &= 0\\ -I_4 - I_5 + I_6 &= 0\\ I_1 + 2I_2 + 5I_5 &= 10\\ 2I_2 -3I_3 + 4I_4 &= 0\\ -4I_4 + 5I_5 - 6I_6 &= 0 \end{aligned} \]

系数行列式A, 常数向量b：

\[A= \begin{vmatrix} 1 & -1 & -1 & 0 & 0 & 0\\ 0 & 1 & 0 & -1 & -1 & 0\\ 0 & 0 & -1 & -1 & 0 & 1\\ 1 & 2 & 0 & 0 & 5 & 0\\ 0 & 2 & -3 & 4 & 0 & 0\\ 0 & 0 & 0 & -4 & 5 & -6 \end{vmatrix}, b= \begin{vmatrix} 0\\ 0\\ 1\\ 0 \\ 0\\ -6 \end{vmatrix} \]

可求得\(A=-587\)

根据克莱姆法则，\(A\neq 0\)，方程组有唯一解：

\[\begin{aligned} (I_1,I_2,I_3,I_4,I_5,I_6) &= (x_1,x_2,x_3,x_4,x_5,x_6)\\ &= (\frac{|B_1|}{|A|},\frac{|B_2|}{|A|},\frac{|B_3|}{|A|},\frac{|B_4|}{|A|},\frac{|B_5|}{|A|},\frac{|B_6|}{|A|}) \end{aligned} \]

而\(|B_i|\)是系数行列式\(|A|\)的第i列用常数向量b替换，而得到的行列式，例如：

\[|B_5|= \begin{vmatrix} 1 & -1 & -1 & 0 & \bm{0} & 0\\ 0 & 1 & 0 & -1 & \bm{0} & 0\\ 0 & 0 & -1 & -1 & \bm{0} & 1\\ 1 & 2 & 0 & 0 & \bm{10} & 0\\ 0 & 2 & -3 & 4 & \bm{0} & 0\\ 0 & 0 & 0 & -4 & \bm{0} & -6 \end{vmatrix} =-660 \]

∴\(I_5=x_5=\frac{|B_5|}{|A|}=1.124A\)
∴\(V_5=I_5R_5=1.124A*5Ω=5.62V\)

参考

[1]美 舍茨 Scherz, Paul.实用电子元器件与电路基础[M].电子工业出版社,2009.