SoftGLRender源码：轨道控制器（OrbitController）

目录

• 特性
• 轨道控制器模型
• OrbitController类
  • 类声明
  • 构造与析构
  • 更新相机的观察者信息
  • 平移控制
  • 旋转控制
  • 缩放控制
  • 控制参数
• SmoothOrbitController类
  • 类声明
  • 构造与析构
  • 实现平滑效果
  • 重置控制器
• 参考

特性

文件：OrbitController.h, OrbitController.cpp

这部分负责视角切换，改变相机在空间坐标系中的位置、朝向，方便从不同角度观察物体. 我们把这部分称为观察者信息，用于构建相机的观察坐标系.

• 轨道控制器能响应鼠标事件：按住鼠标左键移动鼠标，松开左键移动鼠标，滑动滚轮(main.cpp中注册回调)
• 调整相机在世界坐标系中的位置
• 更新相机坐标后，重新渲染画面

观察者信息，通常由用户指定，包含：

1）眼睛位置\(\bm{e}\)；
2）观察方向\(\bm{g}\)；
3）初始观察向上向量\(\bm{t}\)

通过2个类实现：

1）OrbitController（基础轨道控制器），管理相机的观察者信息.

\[\begin{aligned} \bm{e} &=eye\_\\ \bm{g} &=center\_ - eye\_\\ \bm{t} &= up\_ \end{aligned} \]

2）SmoothOrbitController（平滑轨道控制器），提供平滑的过渡效果（如惯性衰减）

轨道控制器模型

轨道控制器原理框图：

相机变换（视图变换），参见：计算机图形：mvp变换（模型、视图、投影变换）

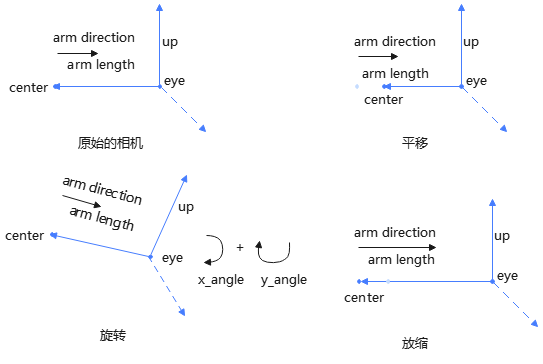
轨道控制器如何通过捕获的UI事件来控制观察者信息的呢？

主要通过鼠标事件，控制center位置、手臂方向（arm direction）、手臂长度（arm length），进而控制相机的位置（eye）、观察点（center）、观察向上向量（up）等.

OrbitController类

类声明

class OrbitController {
public:
	explicit OrbitController(Camera& camera);
	void update();
	void panByPixels(double dx, double dy);
	void rotateByPixels(double dx, double dy);
	void zoomByPixels(double dx, double dy);
	void reset();

private:
	Camera& camera_;

	glm::vec3 eye_{};    // 摄像机位置
	glm::vec3 center_{}; // 目标点
	glm::vec3 up_{};     // 观察向上向量

	float armLength_ = 0.f; // arm length, 手臂长度
	glm::vec3 armDir_{};    // arm direction, 手臂方向

	float panSensitivity_    = 0.1f;
	float zoomSensitivity_   = 0.2f;
	float rotateSensitivity_ = 0.2f;
};

主要数据成员：

• camera_ 负责维护相机，用于透视投影
• eye_ 眼镜位置
• center_ 目标点，眼睛看向的物体中心位置，决定了观察方向
• up_ 相机向上向量
• armLength_ 轨道控制器的手臂长度
• armDir_ 轨道控制器的手臂方向
• panSensitivity_ 平移系数
• zoomSensitivity_ 放缩系数
• rotateSensitivity_ 旋转系数

问题：Camera类中，也有eye_、center_、up_属性，为什么这里要多添加一份，而不是直接控制Camera对应属性？

答：这是一种缓存机制. 能确保：
1）封装性. 随意访问Camera属性，可能导致控制逻辑混乱. 用Camera提供的固定接口(Camera::lookAt）设置相机属性，更安全.

2）数据一致性. 用户可能会在短时间内多次调整相机属性（回调），而相机需要在每帧绘制时（主循环），确保相机属性是一个完整的状态.

核心函数：

• panByPixels 平移相机
• rotateByPixels 绕x轴、y轴旋转
• zoomByPixels 缩放（推近/拉远相机）
• reset 重置相机和轨道控制器

构造与析构

OrbitController构造函数中，主要干2件事：
1）利用调用者（ViewManager）传入的Camera对象，初始化camera_属性；
2）重置轨道控制器中的相机属性、手臂长、方向.

注意：OrbitController中缓存的相机模型的属性，跟传入的Camera对象对应的相机模型的属性并不一致. 但只需要在帧绘制（update()）时，（调用Camera::lookAt）保持一致即可.

这也是OrbitController设计得一个比较巧妙的地方，能很好的与Camera类解耦，同时能很好控制Camera属性.

static const glm::vec3 init_eye_   (-1.5, 3, 3);
static const glm::vec3 init_center_(   0, 1, 0);
static const glm::vec3 init_up_    (   0, 1, 0);

OrbitController::OrbitController(Camera& camera) : camera_(camera) {
	reset();
}

void OrbitController::reset() {
	eye_          = init_eye_;
	center_       = init_center_;
	up_           = init_up_;

	glm::vec3 dir = eye_ - center_;
	armDir_       = glm::normalize(dir);
	armLength_    = glm::length(dir);
}

更新相机的观察者信息

OrbitController最终目的：接收用户输入，控制相机空间位置、朝向，便于以不同视角观察场景. 相机在每一帧中都需要用到观察者信息，更新观察坐标系，进而计算投影矩阵.

在ViewManager::drawFrame中调用.

void OrbitController::update() {
	eye_ = center_ + armDir_ * armLength_;
	camera_.lookAt(eye_, center_, up_);
}

平移控制

我们要平移什么？

平移相机（eye），但不平移注视点（center），那么会形成旋转效果；

平移注视点（center），但不平移相机（eye），同样会形成旋转效果.

因此，相机、注视点需要同时平移，不过需要遵守一个原则：

\[eye = center + armDir * armLength \]

∴可以先平移center，然后计算出eye.

通过鼠标滑动回调，能得到鼠标平移信息\((dx,dy)\)，即沿着屏幕x、y轴移动的距离（单位：像素）. 可将其当做center在观察坐标系下的平移.

因为center是一个世界坐标，所以需要先将\((dx,dy)\)转换为世界坐标，再更新center. 等每一帧绘制时，再重新计算相机的观察者信息(eye,center,up).

// 平移控制
// 根据鼠标移动距离(dx, dy)平移center_，实现场景的左右/上下拖动
void OrbitController::panByPixels(double dx, double dy) {
	// 1. 将屏幕像素偏移 (dx, -dy) 转换为世界空间偏移
	glm::vec3 world_offset = camera_.getWorldPositionFromView(glm::vec3(dx, -dy, 0));
	glm::vec3 world_origin = camera_.getWorldPositionFromView(glm::vec3(0));

	// 2. 计算世界空间中的实际移动量
	glm::vec3 delta = (world_origin - world_offset) * armLength_ * panSensitivity_;

	// 3. 更新center_
	center_        += delta;
}

注意：-dy是为了反转竖直方向的平移方向.

旋转控制

我们需要旋转什么？

在旋转控制中，我们需要的是旋转相机，但不改变注视点（center），也无需改变相机与注视点距离（arm length，即手臂长度）.

根据相机位置计算规则：

\[eye = center + armDir * armLength \]

我们能控制的，就是arm direction（手臂方向），即相机的方向向量(Camera Direction Vector).

// 旋转控制
// 根据鼠标移动距离(dx, dy)旋转相机，实现围绕目标点 center_ 的轨道旋转
void OrbitController::rotateByPixels(double dx, double dy) {
	// 1. 计算旋转角度（灵敏度调整）
	float x_angle = (float)dx * rotateSensitivity_;
	float y_angle = (float)dy * rotateSensitivity_;

	// 2. 构造旋转四元数（绕 X 和 Y 轴旋转）
	// glm::qua 代表四元数，表示3D旋转，绕Z->Y->X顺序的旋转（GLM默认顺序）
	glm::qua<float> q = glm::qua<float>(glm::radians(glm::vec3(-y_angle, -x_angle, 0)));

	// 3. 旋转相机的方向向量 armDir_
	// 将方向向量 armDir_，通过四元数q进行旋转，得到新的方向向量
	glm::vec3 new_dir = glm::mat4_cast(q) * glm::vec4(armDir_, 1.0f);
	armDir_           = glm::normalize(new_dir);
}

其中，四元数glm::qua(vec<3, T, Q> const& eulerAngle)代表绕x、y、z轴分别进行旋转（Tait–Bryan角），三个旋转角度分别为\((α,β,γ)\).

缩放控制

我们需要缩放什么？

实践中，我们缩放场景中物体时，并不是直接改变物体尺寸，因为这不符合现实世界逻辑，而是通过靠近、远离目标物体而实现视觉效果上的放大、缩小. 这其实利用了近大远小的效果.

也就是说，我们控制armLength（手臂长度），但不改变center，从而实现靠近、远离目标物体的效果.

// 缩放控制
// 处理鼠标滚轮输入，控制相机与目标点（center_）的距离
void OrbitController::zoomByPixels(double dx, double dy) {
	// 1. 更新相机到目标的距离（armLength_）
	armLength_ += -(float)dy * zoomSensitivity_;

	// 2. 限制最小距离（避免相机穿过目标点或距离过近）
	if (armLength_ < MIN_ORBIT_ARM_LENGTH) {
		armLength_ = MIN_ORBIT_ARM_LENGTH;
	}

	// 3. 重新计算相机位置（eye_）
	eye_ = center_ + armDir_ * armLength_;
}

个人认为，没有必要在这里马上更新eye，可以等到每一帧绘制时统一更新.

控制参数

panSensitivity_，rotateSensitivity_ ，zoomSensitivity_ 分别在平移控制、旋转控制、放缩控制中，在将输入转化为控制参数时，起比例系数的作用.

关于作为谁的比例系数，有2类做法：

1）输入参数乘以对应系数，从输入参数上控制参数的敏感性；
2）在计算结果乘以对应系数，从控制效果上控制参数的敏感性.

SmoothOrbitController类

考虑这样一种场景：我们快速滑动鼠标跨过整个屏幕（如dx=dy=1024 pixels），可能不到0.1秒，但是如果在一帧内相机（如方向向量、到目标的距离）变化幅度太大，可能导致画面切换突兀.

SmoothOrbitController就是这样一个类，在OrbitController基础上，逐帧实现运动效果，类似于惯性，以达到平滑过渡效果.

类声明

// 平滑轨道控制器
// 对 OrbitController 进行封装，提供平滑的过渡效果（如惯性衰减）
class SmoothOrbitController {
public:
	explicit SmoothOrbitController(std::shared_ptr<OrbitController> orbit_controller)
		: orbitController_(std::move(orbit_controller)) {}

	// 每帧调用，处理未完成的运动（缩放、旋转、平移），并逐步衰减输入值（实现平滑效果）
	void update();

	inline void reset() {
		orbitController_->reset();
	}

	// 由外部事件回调传入这些值
	double zoomX   = 0;
	double zoomY   = 0;
	double rotateX = 0;
	double rotateY = 0;
	double panX    = 0;
	double panY    = 0;

private:
	const double motionEps         = 0.001f; // 运动停止的阈值（< 该值, 则停止）
	const double motionSensitivity = 1.2f;   // 运动衰减的敏感度（值越大，停止越快）
	std::shared_ptr<OrbitController> orbitController_;
};

数据成员：

• panX x轴方向平移距离
• panY y轴方向平移距离
• rotateX 绕x轴旋转角度
• rotateY 绕y轴旋转角度
• zoomX x轴方向放缩距离
• zoomY y轴方向放缩距离
• motionEps 运动停止的阈值，当输入数据的某个方向运动距离 < 该阈值时，表示停止运动
• motionSensitivity 运动衰减系数，每帧运动都会在上一次基础上衰减
• orbitController_ Impl惯用法.

impl参见C++ Pimpl惯用法（桥接模式特例） 

这些输入成员，由外部鼠标、键盘事件传入原始数据值(raw value).

核心函数：

• reset() 重置控制器状态
• update() 处理未完成运动，每帧调用.

构造与析构

SmoothOrbitController 只有构造，没有（自定义）析构. 其构造函数很简单，只是将外部传入的shared_ptr管理的OrbitController对象控制权移交给orbitController_成员.

为什么要用std::move，而不是直接赋值？

个人认为都可以，代价都不大. 不过，用std::move剥夺客户对OrbitController对象控制权后，会更安全，避免客户意外调用，从而导致非预期问题.

	explicit SmoothOrbitController(std::shared_ptr<OrbitController> orbit_controller)
		: orbitController_(std::move(orbit_controller)) {}

实现平滑效果

SmoothOrbitController的核心，就是利用update实现鼠标运动控制相机观察的平滑效果.

注意：SmoothOrbitController通过每帧对运动数据的衰减，实现平滑效果，而非直接控制相机的运动. 相机的运动，还是由OrbitController控制.

	// 每帧调用
	void update() {

		// 放缩
		// 只有 > 运动阈值的运动量，才处理
		if (std::abs(zoomX) > motionEps || std::abs(zoomY) > motionEps) {
			// 每次处理后，运动量都要进行衰减
			zoomX /= motionSensitivity;
			zoomY /= motionSensitivity;
			orbitController_->zoomByPixels(zoomX, zoomY);
		}
		else { // < 阈值的运动，直接清0
			zoomX = 0;
			zoomY = 0;
		}

		// 旋转
		if (std::abs(rotateX) > motionEps || std::abs(rotateY) > motionEps) {
			// 衰减
			rotateX /= motionSensitivity;
			rotateY /= motionSensitivity;
			orbitController_->rotateByPixels(rotateX, rotateY);
		}
		else {
			rotateX = 0;
			rotateY = 0;
		}

		// 平移
		if (std::abs(panX) > motionEps || std::abs(panY) > motionEps) {
			orbitController_->panByPixels(panX, panY);
			panX = 0;
			panY = 0;
		}
		// 同步计算并更新相机的观察者信息
		orbitController_->update();
	}

由于每帧都调用update，因此可包含orbitController_的同步更新.

平移运动并没有做衰减处理，为什么？

个人认为：因为相机、目标点同时移动，平移时，场景内容的切换速度尚能接受.

重置控制器

什么时候需要重置控制器？

如果重置了相机，例如客户希望恢复到原始相机位置，那么就需要重置控制器. APP在配置面板UI上（configPanel_），提供了重置相机的reset按钮，因此，在该按钮的回调（resetCameraFunc_）中，会调用reset().

重置什么？

如果能将所有属性都重置，当然没问题；但SoftGLRender只重置了orbitController_.

	inline void reset() {
		// 转发给orbitController_
		orbitController_->reset();
	}

参考

[1] 计算机图形：mvp变换（模型、视图、投影变换）

[2] Marschner S, Shirley P. Fundamentals of computer graphics. 4th edition.[J].World Scientific Publishers Singapore, 2009, 9(1):29-51.DOI:doi:10.1021/i160033a008.

[3] 三维旋转、欧拉角、四元数