计算机图形：光照模型

目录

• 基本概念
• 光源
  • 彩色光源
  • 点光源
  • 无穷远光源
  • 环境光
  • 辐射强度衰减
  • 方向光源、投射效果
  • 角强度衰减
• 表面光照效果
• 基本光照模型
  • 环境光
  • Lambert漫反射模型
  • 镜面反射模型
    • Phong模型
    • Blinn-Phong模型
  • 综合光照模型（OpenGL）
  • 光强与RGB颜色
  • 亮度
• 透明表面
  • 光折射
  • 简单透明模型
• 雾气效果
• OpenGL函数
  • 点光源函数
  • 指定光源位置、类型
  • 指定光源颜色
  • 指定光源的辐射强度衰减系数
  • 方向光源（投射光源）
  • 全局光照参数
  • 表面特性
  • OpenGL光照模型
  • OpenGL雾气效果
  • 透明性函数
• 参考

基本概念

光照明模型（illumination model）：对场景的对象进行透视投影后，用该模型在可见面上产生自然光效果，实现场景的真实感展示. 又称光照模型（lighting model），主要用于对象表面某光照位置的颜色计算.

表面绘制方法（surface rendering method）：使用光照模型为对象的所有投影位置确定像素颜色. 有2种方式确定像素颜色：

1）对每一投影位置应用光照模型；
2）先对表面少数点应用光照模型，然后颜色插值.

明暗模型（shading model）：面绘制过程，也称明暗方法，用于计算表面颜色. 与光照模型区别：表面上单个点的光强度计算模型，称为光照模型；应用光照模型求所有投影的表面位置的像素颜色的计算模型，称为明暗模型.

真实感成像包含2部分：

1）表面特性的精确表示，如透视效果；
2）场景中光照效果的物理描述，如光照模型；

表面光照效果：光的反射、透明性、表面纹理和阴影.

光源

光源（light source：任意发出辐射能量的对象，称为一个光源，它对场景中其他对象的光照效果有贡献.

仅发光的物体，称为光照源；应用中，可能希望建立既是光源又是光反射体的对象，如塑料球内放置一个灯泡，这样球表面既发光也反射光.

彩色光源

人眼对三色值敏感，可将光源建模成红、绿、蓝3个分量的彩色光源. 三元组描述：

\[I=\begin{bmatrix} I_r\\ I_g\\ I_b \end{bmatrix} \]

点光源

点光源（point lighting source）：用RGB 3个分量指定单个颜色的发光体模型，最简单的光源模型. 点光源由位置、发光颜色定义.

常用于：
1）比场景对象小得多的光源；
2）离场景不是很近的大光源；

从点光源发出的光线路径示意图：

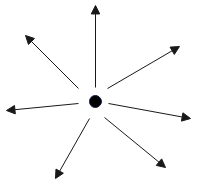
无穷远光源

离场景非常远的大型光源，称为无穷远光源，如太阳，常用作环境光.

远距离光源，仅在一个方向照明场景. 从远距离光源到场景中任意位置的光线路径接近不变.

环境光

环境光（ambient light）：均匀的照明. 如通过安装散光器，让房间内的照明均匀，这种光源就是环境光.
环境光由光照强度三元组\(I_a\)表征，场景中任意一点\(I_a\)相同.
环境光强度有R、G、B 3个分量：

\[I_a=\begin{bmatrix} I_{ar}\\ I_{ag}\\ I_{ab} \end{bmatrix} \]

三个分量分别代表红、绿、蓝分量强度.

tips：场景每个位置的环境光照强度相同，但不同表面的反射不一样，因为材质不同.

辐射强度衰减

辐射光线从一点光源发出，并在空间中传播，距离光源为\(d_l\)时，其振幅按因子\(1/d_l^2\). 含义：接近光源的表面入射光强度更高，远离的更低.

光照模型中，必须考虑光强度衰减，否则难以得到真实感光照效果.

实际应用中，由于靠近点光源时，\(1/d_i^2\)变化幅度大，而远离光源时，变化很小，从而导致不能产生真实感图形. 因此，常用d的2次多项式计算衰减因子：

\[\tag{1} f_{l,radatten}(d_l)= \begin{cases} 1, & 光源在无穷远处\\ {1\over a_0+a_1d_l+a_2d_l^2}, & 光源是局部光源 \end{cases} \]

用户可调整常数\(a_0, a_1, a_2\)的值，得到不同光照效果. i.g. 当\(d_l\)非常小时，可赋予\(a_0\)大值来防止\(f_{l,radatten}(d_l)\)值变得太大.

方向光源、投射效果

对局部光源修改，可得到方向光源或投影光束.

建立方向光源（或称投影光源）：除了位置、颜色外，还需一个向量方向+角度范围\(θ_t\). 这将定义以光源向量方向为轴的一个圆周.

记\(V_{light}\)为光源方向的单位向量，且记\(V_{obj}\)为从光源位置到一个对象位置的方向上的单位向量. 则，

\[\tag{2} \bm{V_{obj}}\cdot \bm{V_{light}}=\cos \alpha \]

其中，α是光方向向量到对象的角距离.

如果将光圆锥角度限制为\(\theta_l \in (0°, 90°]\)，当\(\cos \alpha >= \cos \theta_l\)时，则对象位于光锥体内；否则，则对象位于光锥体外.

方向点光源：

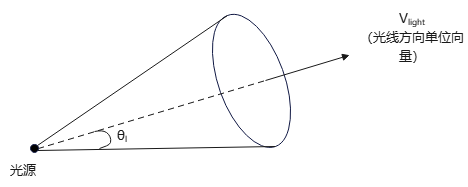
方向点光源照明对象（三棱锥）：

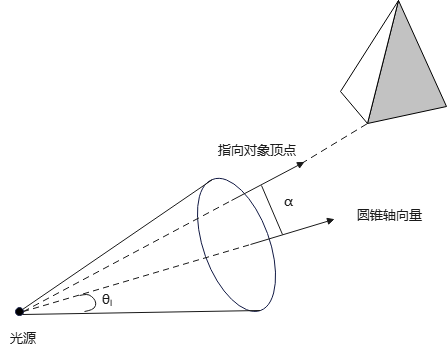
角强度衰减

方向光源按光强度角度计算衰减. 衰减函数：

\[\tag{3} f_{angatten}(\varPhi)=\cos ^{a_l}\varPhi, 0°\le \varPhi \le \theta \]

其中，衰减指数\(a_l\)赋以某个正值；角\(\varPhi\)从圆锥轴开始计算，圆锥轴上，\(\varPhi=0\).

光强度函数要考虑几个特殊情况：
1）如果光源不是方向光源（即不是投影光源），则没有角强度衰减；
2）如果对象位于投影光圆锥体外，则得不到该光源的光照.

角强度衰减一般公式：

\[\tag{4} f_{l,angatten}=\begin{cases} 1.0, & 光源不是投影光源\\ 0.0, & 对象位于投射圆锥外(\bm{V_{obj}}\cdot \bm{V_{light}}=\cos \varPhi < \cos \theta) \\ (\bm{V_{obj}}\cdot \bm{V_{light}})^{a_l}, & 其他 \end{cases} \]

其中，\(\bm{V_{obj}}\)是光源到对象位置的方向的单位向量；\(\bm{V_{light}}\)是（投影）光源的方向的单位向量，且平行于光圆锥体轴线. \(\bm{V_{obj}}\cdot \bm{V_{light}}\)相当于\(\cos \varPhi\).

表面光照效果

光照模型使用为表面设定的各种光学特性计算表面的光照效果，特性包括：透明度、颜色反射系数、各种表面纹理参数.

• 特性对光照效果的影响

不透明度：当光入射到不透明表面时，一部分被反射，另一部分被吸收. 入射光反射量取决于材料类型. 光亮表面反射光较多，灰暗表面吸收光较多.

漫反射（diffuse reflection）：粗糙或颗粒状表面会将反射光向各方向散去的现象. 粗糙、不光滑的表面，主要产生漫反射，因而各角度看表面亮度相同. 对象漫反射光的颜色，称为该对象的颜色，如物体表现为黑色，是因为所有入射光被吸收.

镜面反射（specular reflection）：有些反射光会集中成醒目的或明亮的一个点. 表面光亮比灰暗发生得更多，如抛光的金属.

背景光（background light）或环境光（ambient light）：场景中各表面的反射光生成的光照效果，致使对象不暴露在光源下也仍可见.

基本光照模型

用光照效果的物理过程近似表示，可简化计算.

光照模型中，发光体一般限于点光源. 不过，很多图形软件包也提供处理方向光源（投射光源）的函数.

环境光

用参数\(I_a\)表示环境光层次.
设定场景一般亮度级 => 背景光 => 各照明表面全局漫反射

Lambert漫反射模型

理想漫反射体（ideal diffuse reflectors）：假设入射光在各个方向以相同强度发散而与观察位置无关，这样的表面称为理想漫反射体.
朗伯余弦定律（Lambert's cosine law）：也称朗伯反射体（Lambertian reflectors），描述光散射的一种定律，表明光散射强度与观察角的余弦成正比，即：

\[\tag{5} I(\theta)=I_N\cos \theta \]

其中，\(I(\theta)\)指与法向量成\(\theta\)角的散射强度，\(I_N\)指观察角度为0（法线方向）处的散射强度，\(\theta\)指观察角度（与入射点处物体表面的法向量角度），范围[0, 1].

对于朗伯反射，（同一物体）所有观察方向的光强度都相同.

由于物体表面粗糙程度、材质不同，对光的反射效果也不同，确定一个参数\(k_d\)作为物体表面反射率，称为漫反射系数（diffuse reflection coefficient）或漫反射率（diffuse reflectivity）.

对于环境光\(I_a\)，其漫反射光强为：

\[\tag{6} I_{ambdiff}=k_dI_a \]

其中，\(k_d\)为漫反射系数.

当入射光l⊥物体表面时，得到最多光照；当入射光与法线方向成一定角度θ（即入射角）时，得到更少光照，此时，强度为\(I_l\)的光源的有效入射光为：

\[\tag{7} I_{l,incident}=I_l\cos\theta \]

相当于入射光垂直于物体表面的分量，才是有效光照.

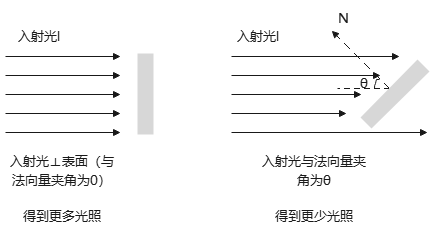
于是，物体表面对光源\(I_l\)的漫反射光强度为：

\[\tag{8} \begin{aligned} I_{l,diff}&=k_dI_{l,incident}\\ &=k_dI_l\cos\theta \end{aligned} \]

记\(\bm{N}\)法线方向单位向量，\(\bm{L}\)入射光反向的单位向量. 一个点光源漫反射可表示为：

\[\tag{9} I_{l,diff}=\begin{cases} k_dI_l(\bm{N}\cdot \bm{L}), & \bm{N}\cdot \bm{L} >0（光源位于表面前）\\ 0.0, & \bm{N}\cdot \bm{L} \le 0 （光源位于表面后） \end{cases} \]

如果是环境光和点光源的组合，则漫反射可表示为：

\[\tag{10} I_{diff}=\begin{cases} k_aI_a+k_dI_l(\bm{N}\cdot \bm{L}), & \bm{N}\cdot \bm{L} > 0\\ k_aI_a, & \bm{N}\cdot \bm{L} \le 0 \end{cases} \]

其中，\(k_a、k_d\)分别表示表面对环境光、点光源的漫反射率，取决于表面材质.

如果点光源考虑距离衰减，Lambert漫反射模型可写为：

\[\tag{11} \begin{aligned} I_{diff}&=\begin{cases} k_aI_a+fk_dI_l(\bm{N}\cdot \bm{L}), & \bm{N}\cdot \bm{L} > 0\\ k_aI_a, & \bm{N}\cdot \bm{L} \le 0 \end{cases}\\ f&=max({1\over c_1+c_2d+c_3d^2},1) \end{aligned} \]

其中，f为光强衰减因子，\(c_1,c_2,c_3\)为用户确定的常数.

镜面反射模型

反射=漫反射+镜面反射

光滑表面上看到的高光或镜面反射，是由接近镜面反射角（specular-reflection angle）的一个汇聚区域内，入射光全部或绝大部分被反射导致.

特点：镜面反射角=入射角.

镜面反射示意图：

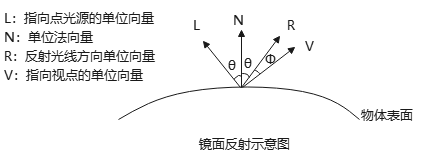
其中，\(\bm{L}\)是入射光线反方向，\(\bm{N}\)是法向量方向，\(\bm{R}\)是反射光线方向，\(\bm{V}\)是观察方向的反方向. 入射角=反射镜=θ.

对于理想镜面反射，当\(\bm{V}\)与\(\bm{R}\)重合时（Φ=0），才能观察到反射光线；
对于非理想镜面反射，反射光线分布在向量R周围.

Phong模型

Phong镜面反射模型（Phong specular-reflection model）：简称Phong模型（Phong model），镜面反射光强度与\(\cos^nΦ\)成正比. 其中，\(Φ\in [0°, 90°]\).

Phong模型镜面反射可表示为：

\[\tag{12} I_{l,spec}=W(\theta)I_l\cos^{n_{s}} Φ \]

其中，\(I_l\)为光源强度，Φ为观察方向与镜面反射方向R的夹角.
W(θ)（θ入射角）为镜面反射系数（specular-reflection coefficient），近似表示单色镜面反射光强度的变化，因为镜面反射的光强主要由表面材质、入射角及其他属性（极性、入射光颜色等）决定. 范围\([0,1]\).
\(n_s\)为镜面反射参数（specular-reflection exponent），由表面材质决定：表面越光滑，值越大；越粗糙，值越小（到1）. 理想反射器\(n=+∞\).

对于透明材质（如玻璃），θ接近90°时才表现出镜面反射；
对于不透明材质（如粉笔），几乎所有入射角的镜面反射均为常量，可用常数\(k_s\)替代W(θ). 而\(cos Φ\)能用向量内积\(V·R\)得到，因此，式(12)对应点光源的镜面反射可写成：

\[\tag{13} I_{l,spec}=\begin{cases} k_sI_l(\bm{V}\cdot \bm{R})^{n_s}, & \bm{V}\cdot \bm{R} > 0\space and\space \bm{N}\cdot \bm{L} > 0\\ 0.0, & \bm{V}\cdot \bm{R} \le 0 \space or \space \bm{N}\cdot \bm{L} \le 0 \end{cases} \]

\(\bm{V}\cdot \bm{R}>0\)：视点在表面前方；\(\bm{V}\cdot \bm{R}\le0\)：视点在表面后方.

\(\bm{N}\cdot \bm{L}>0\)：光源在表面前方；\(\bm{N}\cdot \bm{L}<0\)：光源在表面后方.

如何得到向量\(\bm{R}\)？

\(\bm{N}·\bm{L}=|\bm{N}||\bm{L}|cosθ=|\bm{N}||\bm{L}'|=|\bm{L}'|\), \(\bm{L}'\)是\(\bm{L}\)在\(\bm{N}\)上投影

∴\(\bm{R}+\bm{L}=2\bm{N}(\bm{N}·\bm{L})\)

∴\(\bm{R}=2\bm{N}(\bm{N}·\bm{L})-\bm{L}\)

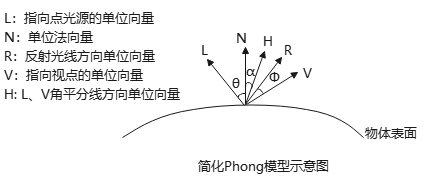
Blinn-Phong模型

Blinnn-Phong模型是简化的Phong模型，而Phong模型是纯几何模型. 因为求解向量\(\bm{R}\)麻烦，因此，实践中常用Blinn-Phong模型，用半角向量（halfway vector），又称半程向量（half vector），\(\bm{H}={\bm{L}+\bm{V}\over |\bm{L}+\bm{V}|}\)计算镜面反射范围，用点积\(\bm{N}\cdot \bm{H}\)替代\(\bm{V}\cdot \bm{R}\)，经验值\(cos α\)替代\(cos Φ\). 当向量V与\(L、R\)共面时，\(α=Φ/2\)；否则，\(α>Φ/2\).
事实上，可以推导出\(Φ=α/2\)（证明很简单，略）.

\[I_{l,spec}=\begin{cases} k_s\cdot I_l \cdot (\bm{N}\cdot \bm{H})^{n_s}, & \bm{N}\cdot \bm{H}>0 \space and\space \bm{N}\cdot \bm{L} > 0\\ 0 & \bm{N}\cdot \bm{H}\le 0\space or \space \space \bm{N}\cdot \bm{L}\le 0 \end{cases} \]

• 漫反射结合镜面反射

对于单点光源，如果表面某点结合漫反射、镜面反射，光照模型可写为：

\[\tag{14} \begin{aligned} I&=I_{diff}+I_{spec}\\ &=k_aI_a+k_dI_l(\bm{N}\cdot \bm{L})+k_sI_l(\bm{N}\cdot \bm{H})^{n_s} \end{aligned} \]

当然，如果光源位于表面后面，则只有环境光，其他反射光为0.

• 多点光源的漫反射和镜像反射

对于多个点光源，在任一表面点叠加各光源效果（环境光反射、漫反射、镜面反射）：

\[\tag{15} \begin{aligned} I&=I_{ambdiff}+\sum_{l=1}^n[I_{l,diff}+I_{l,spec}]\\ &=k_aI_a+\sum_{l=1}^n I_l[k_d(\bm{N}\cdot \bm{L})+k_s(\bm{N}\cdot \bm{H})^{n_s}] \end{aligned} \]

如果考虑衰减（距离衰减、角度衰减），就要在光强上乘以对应衰减因子.

综合光照模型（OpenGL）

OpenGL使用这一基本模型.

考虑多光源、（距离、角度）衰减因子、方向光效果（高光）、无穷远光源、发光表面的表面反射的照明模型（适用单色、多色）：

\[\tag{16} I=I_{surfemission}+I_{ambdiff}+\sum_{l=1}^nf_{l,radatten}f_{l,angatten}(I_{l,diff}+I_{l,spec}) \]

其中，\(I_{surfemission}\)表示表面光发射光强，是材质本身发射的光，但不参与其他对象的照明；\(I_{ambdiff}\)是环境光光强；n代表光源个数；\(f_{l,radatten}\)表示光源的距离衰减因子；\(f_{l,angatten}\)表示光源的角度衰减因子；\(I_{l,diff}\)表示漫反射光强；\(I_{l,spec}\)表示镜面反射光强.

\(I_{ambdiff}\)计算：

\[I_{ambdiff}=k_aI_a \]

其中，\(k_a\)是环境光反射系数，\(I_a\)是环境光光强.

\(f_{l,radatten}\)计算：

\[f_{l,radatten}=\begin{cases} 1, & 光源在无穷远处\\ \frac{1}{a_0+a_1d_l+a_2d_l^2}, & 光源是局部光源 \end{cases} \]

其中，\(a_0,a_1,a_2\)是常数，用户可调整；\(d_l\)是对象到光源距离.

\(f_{l,angatten}\)计算：

\[f_{l,angatten}=\begin{cases} 1.0, & 光源不是投影光源（方向光源）\\ 0.0, & 对象位于投射光圆锥体外 \\ (V_{obj}\cdot V_{light})^{a_l}, & 其他 \end{cases} \]

其中，\(V_{obj}\)是光源到对象位置的单位向量；\(V_{light}\)是投影光源方向的单位向量.

\(I_{l,diff}\)计算：

\[I_{l,diff}=\begin{cases} 0.0, & \bm{N}\cdot \bm{L_l}\le 0.0(光源在对象后面)\\ k_dI_l(\bm{N}\cdot \bm{L_l}), & 其他 \end{cases} \]

其中，\(k_d\)是漫反射系数，\(I_l\)是光源在表面的入射光强，\(\bm{N}\)是表面单位法向量，\(\bm{L}\)是入射点到光源方向的单位向量. \(\bm{N}\cdot \bm{L_l}\)相当于\(\cos θ\)，而\(θ\)是法向量和到光源方向的夹角.

\(I_{l,spec}\)计算：

\[I_{l,spec}=\begin{cases} 0.0, & \bm{V}\cdot \bm{R}\le 0\space or \space \bm{N}\cdot \bm{L} \le 0\\ k_sI_l(\bm{N}\cdot \bm{H})^{n_s}, & \bm{V}\cdot \bm{R}>0 \space and \space \bm{N}\cdot \bm{L} > 0 \end{cases} \]

其中，\(k_s\)是镜面反射系数；\(I_l\)是对象入射光强；\(n_s\)是镜面反射指数，由表面材质决定；\(\bm{V}、\bm{R}\)分别是入射点到视点方向的单位向量、反射光线的单位向量；\(\bm{N}、\bm{L}\)分别是单位法向量、对象到光源方向的单位向量.

\(\bm{V}\cdot \bm{R}\le 0\)代表视点在对象表面后方；反之，代表视点在对象表面前方.
\(\bm{N}\cdot \bm{L} \le 0\)代表光源在对象表面后方；反之，代表光源在对象表面前方.

光强与RGB颜色

光照模型中，
对于每个光源，每个光照强度包含红、绿、蓝3分量，可表示为

\[\tag{17} I_l=(I_{lR},I_{lG},I_{lB}) \]

• 反射系数

对于反射系数，也可用分量表示. 环境光反射：\(k_a=(k_{aR},k_{aG},k_{aB})\)，漫反射：\(k_d=(k_{dR},k_{dG},k_{dB})\)，镜面反射：\(k_s=(k_{sR},k_{sG},k_{sB})\).

例如，一个点光源的漫反射模型可写为：

\[I_{lR,diff}=k_{dR}I_{lR}(\bm{N}\cdot \bm{L_l})\\ I_{lG,diff}=k_{dG}I_{lG}(\bm{N}\cdot \bm{L_l})\\ I_{lB,diff}=k_{dB}I_{lB}(\bm{N}\cdot \bm{L_l}) \]

模型为什么要针对不同颜色设计不同反射系数？
因为如果各种颜色反射相同，即与颜色无关，镜面反射光线与入射光线相同（白色），会使物品看起来像塑料，而实际不同颜色物体对不同颜色光反射不同.

• 反射的颜色分量

也可将反射参数固定为常数，为每个表面定义漫反射、镜面反射的颜色向量. 漫反射的表面颜色向量：\((S_{dR},S_{dG},S_{dB})\)，镜面反射的表面颜色向量：\((S_{sR},S_{sG},S_{sB})\).
例如，一个点光源的蓝色漫反射模型可写为：

\[I_{lB,diff}=k_{d}S_{dB}I_{lB}(\bm{N}\cdot \bm{L_l}) \]

亮度

亮度（luminance）是颜色的一种特征，也称光能量，给出了颜色亮或暗的程度信息.

物理上，颜色用可见辐射能（光）的频率范围来描述，而亮度按在特定照明中的强度成分的加权总和来计算. 实际光照包含连续范围的波长，亮度可表示为：

\[\tag{18} 亮度=\int_{visible \space f}p(f)I(f)df \]

其中，f表示光频率，I(f)表示在特定方向辐射的波长为f的光成分；p(f)表示按经验确定的比例函数，按频率和光照程度而变化.

对于RGB光源的亮度，绿色分量贡献最大，蓝色最小，因此亮度计算：

\[\tag{19} 亮度=0.299R+0.587G+0.114B \]

透明表面

透明的（transparent）：透过对象，能看到后面的东西. 只有折射.
不透明的（opaque）：不能透过对象看到后面的东西. 只有反射.
半透明的（translucent）：介于两者之间. 同时有折射和反射.

光折射

光折射（refraction）：当光线入射到一个透明对象表面时，一部分光线被反射，另一部分被折射. 可模拟真实透明效果.

Snell定律，即光的折射定律：

\[\sin \theta_r={\eta_i\over \eta_r}\sin \theta_i \]

其中，\(\theta_i\)是入射角，也是反射角；\(\eta_i\)是入射材料的折射率，\(\eta_r\)是折射材料的折射率.

• 折射率

折射率取决于材质、温度、入射光波长等参数. 白光的各种彩色成分（波长不同），会以不同角度折射. 通常用平均折射率描述材料的折射率. 空气的折射率常设为1.

如何得到折射方向单位向量\(\bm{T}\)？
结论：

\[\tag{20} \bm{T}=({\eta_i\over \eta_r}\cos \theta_i - \cos \theta_r)\bm{N}-{\eta_i\over \eta_r}\bm{L} \]

证明：

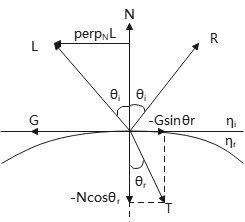
向量L中与向量N垂直的分量\(perp_NL=\bm{L}-\bm{N}(\bm{L}\cdot \bm{N})\)（即L沿方向N的外射影），而在L为斜边的直角三角形中，模\(|perp_NL|=|\bm{L}|\sin \theta_i=\sin \theta_i\)

\(\bm{G}\)⊥\(\bm{N}\)，有\(\bm{G}//{perp_NL}\)
因此，

\[\bm{G}={perp_NL\over |perp_NL|}={\bm{L}-\bm{N}(\bm{L}\cdot \bm{N})\over \sin \theta_i} \]

\(\bm{T}\)可分解为\(\bm{N},\bm{G}\)方向上的2个分量：\(perp_GT=-\bm{N}\cos\theta_r, perp_NT= -\bm{G}\sin\theta_r\)
因此，

\[\begin{aligned} \bm{T}&=perp_GT+perp_NT\\ &=(-\bm{N}\cos\theta_r)*1+(-\bm{G}\sin\theta_r)*1\\ &=({\sin\theta_r\over \sin\theta_i}\cos\theta_i-\cos\theta_r)\bm{N}-{\sin\theta_r\over \sin\theta_i}\bm{L}\\ &=({\eta_i\over \eta_r}\cos \theta_i - \cos \theta_r)\bm{N}-{\eta_i\over \eta_r}\bm{L} (由Snell定律) \end{aligned} \]

注意：\(\bm{T}\)是单位向量，因此\(|\bm{T}|=1\)；\(perp_GT\)是\(\bm{T}\)沿着\(\bm{G}\)方向的外射影（也是向量），因此与\(\bm{N}\)同向；\(perp_NT\)是\(\bm{T}\)沿着\(\bm{N}\)的外射影，因此与\(\bm{G}\)同向.

简单透明模型

不考虑折射导致的路径平移，假定：各对象折射率不变、折射角=入射角.

对象表面总光强：

\[\tag{21} I=(1-k_t)I_{refl}+k_tI_{trans} \]

其中，\(k_t、(1-k_t)\)分别为透明系数、不透明因子（opacity factor），范围0~1.

通过深度优先（从后到前），可混合任意多透明和不透明对象的光照效果.

雾气效果

雾气效果是光照模型有时会考虑的一个因素. 雾气使颜色变淡、对象变模糊.

指数衰减函数模拟雾气效果：

\[\tag{22} f_{atmo}(d)=e^{-ρd} \]

或者，

\[\tag{23} f_{atmo}(d)=e^{-(ρd)^2} \]

其中，d表示观察位置到对象的距离；ρ表示雾气的正密度，较大ρ值，对应稠密的雾气且表面柔和.

有时需要混合雾气颜色、对象颜色：

\[\tag{24} I=f_{atom}(d)I_{obj}+[1-f_{atom}(d)]I_{atom} \]

其中，\(f_{atom}\)表示指数衰减或线性雾气衰减函数，\(I_{obj}\)表示对象颜色，\(I_{atom}\)表示雾气颜色.

OpenGL函数

OpenGL函数支持基本光照模型中的设置点光源、选择表面反射系数、选择其他参数等功能. 还支持模拟透明性、平面绘制、Gouroud表面绘制显示对象.

点光源函数

设置一个点光源特性（位置、类型、颜色、衰减、投射效率等）：

// lightName 标识一个光源
// lightProperty 指定要设置的光源属性
// propertyValue 指定要设置的光源属性值
glLight*(lightName, lightProperty, propertyValue);

后缀码i或f表示参数的数据类型，向量+v，此时propertyValue是一个指向数组的指针.
每个光源用一个标识符引用，参数lightName用8个OpenGL符号标识（GL_LIGHT0,1...7）（有的实现支持>8个光源）.
lightProperty可用10个OpenGL符号属性常数赋值.

• 点亮光源

相当于指定光源的开关.

glEnable(lightName);

• 激活OpenGL光源

相当于全局光源开关.

glEnable(GL_LIGHTING);

光源激活后，对象表面就会用每个光源的光照贡献进行绘制.

指定光源位置、类型

光源属性lightProperty=GL_POSITION，可设置光源2个特性：光源位置、光源类型（light-source type）.
对应属性值propertyValue用一个四元数浮点数的向量表示，前3个元素给出世界坐标位置，第4个指定光源类型. 第4个元素值为0.0，代表无穷远光源（即方向光源）；值为1.0，代表局部光源（即位置光源）.

例，设置2个光源位置、类型：光源1是位置(2.0,0.0,3.0)的局部光源，光源2是位置(2.0,0.0,3.0)的一个在-y方向发射的远光源.

GLfloat light1PosType[] = {2.0,0.0,3.0,1.0};
GLfloat light2PosType[] = {0.0,1.0,0.0,0.0};

glLightfv(GL_LIGHT1, GL_POSITION, light1PosType);
glEnable(GL_LIGHT1);

glLightfv(GL_LIGHT2, GL_POSITION, light2PosType);
glEnable(GL_LIGHT2);

如果不设置光源位置、类型，则默认值(0.0,0.0,1.0,0.0)，即在-z方向发射的光线的远光源.

指定光源颜色

OpenGL光源有三个不同的RGBA颜色特性（用符号颜色特性常量表示）：

1）GL_AMBIENT 对场景环境光有贡献；
2）GL_DIFFUSE 用于漫发射光照计算；
3）GL_SPECULAR 用于镜面反射光照计算；

虽然一个光源只有一种颜色，但可用三个OpenGL光源颜色建立各种光照效果.
注意：alpha分量（不透明因子）只有激活了颜色混合函数激活后才有效.

例，设定一个局部光源的环境光为黑色，标号GL_LIGHT3，且光源的漫反射、镜面反射颜色为白色

GLfloat blackColor[] = {0.0, 0.0, 0.0, 1.0};
GLfloat whiteColor[] = {1.0, 1.0, 1.0, 1.0};

glLightfv(GL_LIGHT3, GL_AMBIENT, blackColor);
glLightfv(GL_LIGHT3, GL_DIFFUSE, whiteColor);
glLightfv(GL_LIGHT3, GL_SPECULAR, whiteColor);

指定光源的辐射强度衰减系数

设置局部光源的距离衰减系数.

例，设置局部光源6的距离衰减系数

glLightfv(GL_LIGHT6, GL_CONSTANT_ATTENUATION, 1.5);
glLightfv(GL_LIGHT6, GL_LINEAR_ATTENUATION, 0.75);
glLightfv(GL_LIGHT6, GL_QUADRATIC_ATTENUATION, 0.4);

常数GL_CONSTANT_ATTENUATION对应下式\(a_0\), GL_LINEAR_ATTENUATION对应\(a_1\), GL_QUADRATIC_ATTENUATION对应\(a_2\).

光源的距离衰减系数计算公式：

\[f_{l,radatten}(d_l)=\begin{cases} 1, & 光源在无穷远处\\ \frac{1}{a_0+a_1d_l+a_2d_l^2}, & 光源是局部光源 \end{cases} \]

如果不指定，默认值\(a_0=1.0, a_1=0.0, a_2=0.0\)

方向光源（投射光源）

对于局部光源（非无穷远处），还能指定方向或投射效果，将光线限制在一个圆锥体空间，即方向光源. 前面（参见计算机图形：光照模型）讲过，方向光源由一个代表圆锥轴线方向的向量+一个从轴线开始的空间角度的范围最大值\(θ_l\)即圆锥角决定，由角衰减指数\(a_1\)和轴线到对象入射光线的角度α决定衰减因子\(\cos^{a_1}α\).

当\(α>θ_l\)时，对象位于光锥体之外，光照为0；
当\(α<=θ_l\)时，对象位于光锥体内，光照为光源强度*衰减因子，即\(I_{light}*\cos^{a_1}α\).

GL_SPOT_DIRECTION指定光源的方向，向量的数据类型可以是整型或浮点型.

GL_SPOT_CUTOFF指定最大角度范围\(θ_l\)，可以是180°或0°到90°范围内的任意值.

GL_SPOT_EXPONENT指定衰减指数\(a_1\).

例，设定方向光源GL_LIGHT3的方向（向量）、最大角度范围\(θ_l\)为30°，衰减指数\(a_1\)为2.5.

GLfloat dirVector[] = {1.0, 0.0, 0.0};

glLightfv(GL_LIGHT3, GL_SPOT_DIRECTION, dirVector);
glLightfv(GL_LIGHT3, GL_SPOT_CUTOFF, 30.0);
glLightfv(GL_LIGHT3, GL_SPOT_EXPONENT, 2.5);

如果不指定，默认方向为平行于-z轴方向，即\((0.0, 0.0, -1.0)\)；圆锥角\(θ_l\)默认180°；各个方向光线没有衰减，即没有角衰减.

全局光照参数

glLight*是设置单个光源参数，OpenGL支持设置全局级光源参数，如设置全局环境光的等级、如何计算镜面高光及选择应用于多边形后向面的光照模型.

glLightModel*(paramName, paramValue);

后缀码可为i或f，表明参数值的数据类型，向量+v.

• 全局背景光

glLight + GL_AMBIENT指定单个局部光源的环境光，而glLightModelfv + GL_LIGHT_MODEL_AMBIENT能设置全局的背景光.

例，将场景的总背景光设置为低强度（暗）蓝色，alpha值为1.0.

globalAmbient[] = {0.0, 0.0, 0.3, 1.0};

glLightModelfv(GL_LIGHT_MODEL_AMBIENT, globalAmbient);

如果不设置，默认低强度白色\((0.2, 0.2, 0.2, 1.0)\)（暗灰色）.

• 观察方向向量

镜面反射计算需要确定从表面入射点到观察位置的向量\(\bm{V}\)，该常数单位向量为+z方向，即(0.0, 0.0, 1.0)，是默认方向. 如果不想用默认方向，可以使用位于观察坐标原点实际观察位置来计算\(\bm{V}\)，调用：

glLightModeli(GL_LIGHT_MODEL_LOCAL_VIEWER, GL_TRUE);

实际观察位置计算\(\bm{V}\)会花费较多时间，但也会带来更真实感显示.

而第二个参数使用GL_FALSE（默认）时，不再计算表面的向量\(\bm{V}\).

• 镜面反射颜色和非镜面反射颜色

将每个顶点的光照计算分为两个颜色项：非镜面反射颜色和镜面反射颜色（也叫主颜色和辅助颜色）. 非镜面反射项包括环境光、表面散射和漫反射，纹理图案和非镜面反射颜色先混合，然后和镜面反射颜色混合.

tips: 表面高光叠加上去，镜面反射可能使纹理图案变样.

glLightModeli(GL_LIGHT_MODEL_COLOR_CONTROL, GL_SEPARATE_SPECULAR_COLOR);

如果不用纹理图案，则不必将颜色分开，光照计算效率更高. 默认值（第二个参数）GL_SINGLE_COLOR，即不分开颜色.

• 前向面和后向面

有时需要对象的后向面，但与前向面的光照不同，此时，可调用下面函数对前向面、后向面用2种不同材质进行光照计算.

glLightModeli(GL_LIGHT_MODEL_TWO_SIDE, GL_TRUE);

如果不设置，后向面默认使用前向面材质计算光照.

表面特性

设置表面的反射系数和其他特性：

glMaterial*(surfFace, surfProperty, propertyValue);

后缀码i或f，表示特性值参数的数据类型，向量+v.

1）surfFace可选值：GL_FRONT, GL_BACK, GL_FRONT_AND_BACK；

2）surfProperty：标识表面参数，如\(I_{surf}\)（表面光强），\(k_a\)（环境光反射系数），\(k_d\)（漫反射系数），\(k_s\)（镜面反射系数），\(n_s\)（镜面反射指数）的符号常量. 除\(n_s\)，其他特性均用向量值指定（RGBA分量）.

3）propertyValue：参数surfProperty对应的值.

在描述几何数据前，需要使用一系列glMaterial函数，指定该对象的所有光照特性.

• 表面散射颜色

表面散射颜色RGBA值\(I_{surf}\)用GL_EMISSION表示.

例，将前向面的表面散射颜色设置为浅灰色（白色）.

surfEmissionColor[] = {0.8, 0.8, 0.8, 1.0};

glMaterialfv(GL_FRONT, GL_EMISSION, surfEmissionColor);

如果不设置，默认散射颜色是黑色(0.0, 0.0, 0.0, 1.0).

tips: 表面散射颜色被认为是材质本身的颜色，并不照明其他对象.

• 表面反射系数

GL_AMBIENT、GL_DIFFUSE、GL_SPECULAR分别表示环境光反射系数、漫反射系数、镜面反射系数.

实践中，常将环境光和漫反射系数设置为相同向量值，此时可用GL_AMBIENT_AND_DIFFUSE.

GL_SHININESS表示镜面反射指数，值可设范围为0~128. 默认值0.

例，设置环境光和漫反射系数为相同值，镜面反射系数为另一值，镜面反射指数为25.0

diffuseCoeff[] = {0.2, 0.4, 0.9, 1.0};
specularCoeff[] = {1.0, 1.0, 1.0, 1.0};

glMaterialfv(GL_FRONT_AND_BACK, GL_AMBIENT_AND_DIFFUSE, diffuseCoeff);
glMaterialfv(GL_FRONT_AND_BACK, GL_SPECULAR, specularCoeff);
glMaterialf(GL_FRONT_AND_BACK, GL_SHININESS, 25.0);

如果不设置，环境光反射系数默认\((0.2, 0.2, 0.2, 1.0)\)，漫反射\((0.8, 0.8, 0.8, 1.0)\)，镜面反射\((1.0, 1.0, 1.0, 1.0)\).

除了RGBA，反射系数也支持用颜色表值设定，特性常量GL_COLOR_INDEXES.

OpenGL光照模型

使用考虑衰减、高光的综合光照模型（见式(16)），但设定参数方面有不同：

1）环境光等级是光源的环境光分量 + 设定的全局环境光分量；
2）漫反射使用光源的漫反射分量计算；
3）镜面反射使用每一个光源的反射分量计算；
4）如果不用局部观察选项，则指定从表面但观察位置（视点）的单位向量V为常数\((0.0, 0.0, 0.0)\).

OpenGL雾气效果

用光照模型计算出表面颜色后，可设定场景中空气的颜色并将表面颜色和雾气颜色混合，然后用雾气强度衰减函数模拟雾气效果.

glEnable(GL_FOG);

glFog*(atmoParameter, paramValue);

后缀码i或f，表示数据类型，向量+v.

• 雾气颜色

atmoParameter=GL_FOG_COLOR 设置一种雾气颜色.

例，将雾气设为蓝灰色

GLfloat atmoColor[4] = {0.8, 0.8, 1.0, 1.0};

glFogfv(GL_FOG_COLOR, atmoColor);

如果不设置，默认黑色\((0.0, 0.0, 0.0, 0.0)\).

• 混合对象颜色、雾气颜色

atmoParameter = GL_FOG_MODE，用雾气的衰减函数混合对象颜色和雾气颜色，即雾气模式.

glFogi(GL_FOG_MODE, atmoAttenFunc);

atmoAttenFunc取值：

1）如果为GL_EXP（默认值），则使用雾气衰减函数式(22)；

2）如果为GL_EXP2，则使用雾气衰减函数式(23)；

3）如果为GL_LINEAR，则使用雾气衰减公式：

\[f=\frac{end-z}{end-start} \]

z表示以观察位置为原点，到对象的距离，即fragment的深度，用户可设定. GL_FOG_START设定雾气距离屏幕多近开始，即start，GL_FOG_END设定雾特效持续到距屏幕多远，即start.

EXP和EXP2雾气，只与GL_FOG_DENSITY有关.

• 雾气密度ρ

计算雾气衰减因子时用. 范围[0,1].

glFogf(GL_FOG_DENSITY, atmoDensity);

默认密度1.0.

透明性函数

• 颜色调和

原理参见简单透明模型（式(21)）.

颜色调和能模拟某些透明效果，但忽略了折射，在多种光照条件或复杂场景下，不能模拟真实透明效果. 如果要实现半透明表面或折射光效，则需要另写子程序.

• 设置alpha值

使用glMaterial和glColor等表面颜色函数时，alpha参数可指定对象为透明的.

例，指定一个透明表面的颜色：

glColor4f(R,G,B,A);

完全透明表面，alpha值即A=1.0；完全不透明，A=0.0.

设置透明值后，激活OpenGL颜色调和功能，并从离观察位置由远到近的次序处理表面.

如果按深度次序处理所有对象，则处理每个透明表面时可关掉深度缓存的写模式，并在处理完后再打开. 可将对象分2类，按如下处理：

glEnable(GL_DEPTH_TEST);
/* 处理所有不透明表面 */

glEnable(GL_BLEND);
glDepthMask(GL_FALSE);
glBlendFunc(GL_ONE_MINUS_SRC_ALPHA, GL_SRC_ALPHA);
/* 处理所有透明表面 */

glDepthMask(GL_FALSE);
glDisable(GL_BLEND);

glutSwapBuffers();

参考

计算机图形学（一）——辐照度学概述 | 博客园

第八章 光照 | ​知乎

[伦吉尔,E.).3D游戏与计算机图形学中的数学方法第3版.清华大学出版社,2016.](https://book.douban.com/subject/26864861/)

glFogi 函数文档 | MSDN