几何体变换到屏幕坐标一般步骤:

观察变换
观察变换(View Transformation):指3D->2D的变换,包括相机变换、投影变换及规范化、视口变换. 主要任务:将3D位置(世界坐标\((x,y,z)\))映射到2D图像坐标(pixel).
而模型变换指设置对象位置、大小、方向.
观察变换包含的3部分:
- 相机变换(Camera Transformation)或眼睛变换(Eye Transformation): 将对象从世界坐标(世界空间)转换到相机的观察坐标(相机空间). 取决于相机位置和方向/姿势.
- 投影变换(Orthographic Projection Transformation): 将相机空间的投影点转换到观察平面(投影平面),进行规范化和裁剪.
- 视口变换(Viewport Transformation)或窗口变换(Windowing Transformation): 将单位图像矩形映射到屏幕空间中的像素矩形.
前面计算机图形:mvp变换(模型、视图、投影变换)讲过MVP变换,包括模型变换、相机变换(视图变换)、投影变换及规范化. 本文主要讲视口变换.
从观察变换角度,物体由原始坐标变换到屏幕空间的示意图:
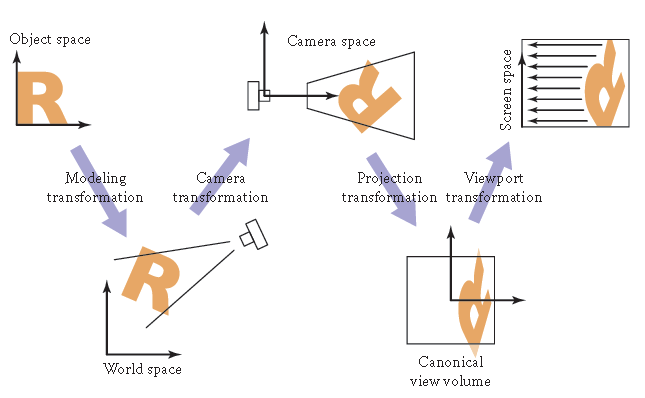
视口变换
几何体经投影变换及规范化后,得到规范化观察体,如何得到屏幕上的图像?
规范化观察体(NDC view volume):将投影观察体中所有点变换成矩形平行管道观察体中的位置,该观察体是坐标范围\((x,y,z)\in [-1,1]^3\)的立方体.
tips: 规范化观察体中物体用NDC坐标(Normalized Device Coordinates, 标准设备坐标)描述.
规范化立方体示意图:

视口变换(Viewport Transformation):将规范化观察体中所有点变换到屏幕上.
规范化观察体与屏幕映射关系:
\[\begin{aligned}
x=-1&\xrightarrow{}屏幕左边,
x=+1\xrightarrow{}屏幕右边\\
y=-1&\xrightarrow{}屏幕下边, y=+1\xrightarrow{}屏幕上边\\
z=-1&\xrightarrow{}深度缓冲0, z=+1\xrightarrow{}深度缓冲1
\end{aligned}
\]
考虑像素宽度
对于拥有\(n_x\times n_y\)像素的屏幕,需将NDC的矩形\([-1,1]^2\)映射到屏幕矩形\([-0.5,n_x-0.5]\times [-0.5,n_y-0.5]\)上. 其中,视口左下角像素坐标\((0, 0)\)
e.g. \(4\times 3\)像素屏幕坐标示意图:
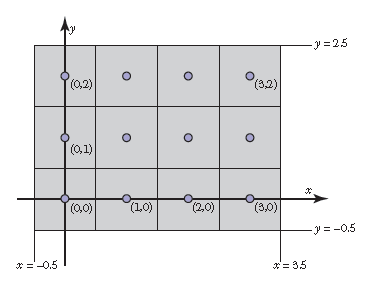
可以看到,像素中心点位于整数坐标值,而像素边界却并没有.
要将规范化观察体上矩形的任一点\((x_{NDC},y_{NDC})\)变换到屏幕\((x_{screen}\\y_{screen})\)位置,可根据点占的横纵比例不变原则计算:
\[\begin{aligned}
\frac{x_{screen}-(-0.5)}{n_x-0.5-(-0.5)}&=\frac{x_{NDC}-(-1)}{1-(-1)}\\
\frac{y_{screen}-(-0.5)}{n_y-0.5-(-0.5)}&=\frac{y_{NDC}-(-1)}{1-(-1)}
\end{aligned}
\]
于是,可得到视口变换:
\[\begin{pmatrix}
x_{screen}\\y_{screen}\\1
\end{pmatrix}
=\begin{pmatrix}
\frac{n_x}{2} & 0 & \frac{n_x-1}{2}\\
0 & \frac{n_y}{2} & \frac{n_y-1}{2}\\
0 & 0 & 1
\end{pmatrix}
\begin{pmatrix}
x_{NDC}\\y_{NDC}\\1
\end{pmatrix}
\]
3D空间下,视口变换矩阵:
\[M_{vp}=\begin{pmatrix}
\frac{n_x}{2} & 0 & 0 & \frac{n_x-1}{2}\\
0 & \frac{n_y}{2} & 0 & \frac{n_y-1}{2}\\
0 & 0 & 1 & 0\\
0 & 0 & 0 & 1
\end{pmatrix}
\]
如果视口左下角坐标不是\((0,0)\), 而是\((x_0,y_0)\),矩形宽高\(n_x\times n_y\). 那么,需将NDC空间\([-1,1]^2\)映射到屏幕空间\([x_0-0.5,x_0+n_x-0.5]\times [y_0-0.5, y_0+n_y-0.5]\)
则视口变换为:
\[\begin{aligned}
\frac{x_{screen}-(x_0-0.5)}{n_x} &= \frac{x_{NDC}-(-1)}{1-(-1)}\\
\frac{y_{screen}-(y_0-0.5)}{n_y} &= \frac{y_{NDC}-(-1)}{1-(-1)}\\
\implies \begin{pmatrix}
x_{screen}\\ y_{screen}\\ 1
\end{pmatrix} &=
\begin{pmatrix}
\frac{n_x}{2} & 0 & x_0 + \frac{n_x - 1}{2}\\
0 & \frac{n_y}{2} & y_0 + \frac{n_y - 1}{2}\\
0 & 0 & 1\\
\end{pmatrix}
\begin{pmatrix} x_{NDC}\\y_{NDC}\\1 \end{pmatrix}
\end{aligned}
\]
不考虑像素速宽度
如果不考虑像素宽度,即认为像素上所有细分点与像素中心在同一屏幕坐标,那么,需将NDC空间\([-1,1]^2\)映射到屏幕空间\([x_0,x_0+n_x]\times [y_0,y_0+n_y]\)
则视口变换为:
\[\begin{aligned}
\frac{x_{screen}-x_0}{x_0+n_x-x_0}&=\frac{x_{NDC}-(-1)}{1-(-1)}\\
\frac{y_{screen}-y_0}{y_0+n_y-y_0}&=\frac{y_{NDC}-(-1)}{1-(-1)}\\
\implies \begin{pmatrix}
x_{screen}\\y_{screen}\\1
\end{pmatrix}
&=\begin{pmatrix}
\frac{n_x}{2} & 0 & x_0+\frac{n_x}{2}\\
0 & \frac{n_y}{2} & y_0+\frac{n_y}{2}\\
0 & 0 & 1
\end{pmatrix}
\begin{pmatrix}
x_{NDC}\\y_{NDC}\\1
\end{pmatrix}
\end{aligned}
\]
其中:
- \((x_0,y_0)\):视口左下角在屏幕中的像素坐标;
- \(n_x,n_y\):视口的宽度和高度(像素);
考虑屏幕深度
不考虑像素宽度情况下,如果我们考虑屏幕的深度值,那么,观察变换又该是什么呢?
设\(depth_{near}, depth_{far}\) 分别是屏幕的近平面和远平面的深度值.
\[z:[-1,1]\ in\ NDC\to depth_{near}, depth_{far}\ in \ Screen \ Space
\]
∴
\[\frac{z_{NDC}-(-1)}{1-(-1)} = \frac{z_{screen}-depth_{near}}{z_{far}-z_{near}}\\
z_{screen} = \frac{depth_{far}-depth_{near}}{2}z_{NDC}+\frac{depth_{far}+depth_{near}}{2}
\]
∴
\[\begin{pmatrix}
x_{screen}\\y_{screen}\\z_{screen}\\1
\end{pmatrix}
=\begin{pmatrix}
\frac{n_x}{2} & 0 & 0 & x_0+\frac{n_x}{2}\\
0 & \frac{n_y}{2} & 0 & y_0+\frac{n_y}{2}\\
0 & 0 & \frac{depth_{far}-depth_{near}}{2} & \frac{depth_{far}+depth_{near}}{2}\\
0 & 0 & 0 & 1
\end{pmatrix}
\begin{pmatrix}
x_{NDC}\\y_{NDC}\\z_{NDC} \\1
\end{pmatrix}
\]
参考
[1] Marschner S , Shirley P .Fundamentals of computer graphics. 4th edition.[J].World Scientific Publishers Singapore, 2009, 9(1):29-51.DOI:doi:10.1021/i160033a008.
[2] 计算机图形:mvp变换(模型、视图、投影变换)







 浙公网安备 33010602011771号
浙公网安备 33010602011771号