【实变函数】01 - 更合理的积分
【本系列目录】
博客总目录
1. 源起
在整理博客之初,我打算从数学最基础的学科开始,逐渐往上建立完整的学科分支。即便不能做到有多细致深入、面面俱到,也要能逻辑自洽、涵盖最核心的脉络。所以整个系列以《集合论》开篇,而后向代数、分析、几何三个方向推进,代数后续包括《实数系统》和《微积分》,以及偏应用的《概率论》和《数理统计》。但想要学习更进阶的随机数学和分析理论,就会碰到许多陌生而基础的障碍,这就是所谓“走得越远,知道的越少”。回头才明白,科学学科的成长犹如一棵大树,要想地上枝繁叶茂,就要根系能绝地三尺。
在任何随机数学的分支里,都会提到其基本定义需要测度论来定义。即便不会真的出现测度论的概念,这样的描述总让我感觉,后面再看下去也只是空中楼阁,所以我们又回到了这样的基础学科。直观上我们能明白测度所讨论内容,大概是对数轴上复杂的集合也定义出“长度”的概念。至于为什么要这样做,还得从我们已经熟悉的积分说起,也就是前面微积分里那个黎曼(Riemann)积分。黎曼积分是对面积的推广,它将图形沿自变量x轴分割成若干条,然后用长方形近似条形的面积。只要条形和长方形的长度随着分割无限逼近(这是非常重要的条件),就可以用长方形面积的极限表示图形面积。
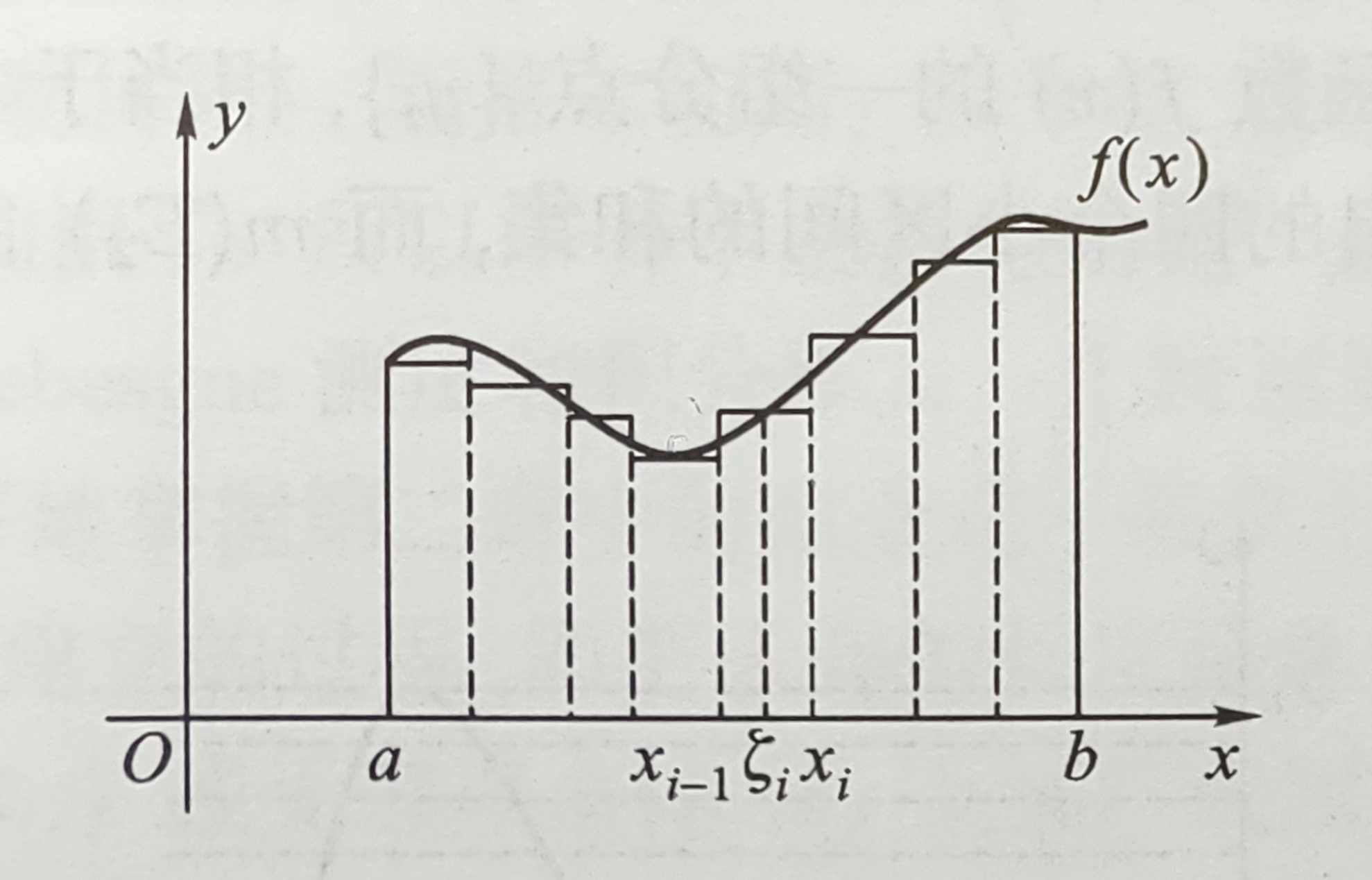
但随着积分使用范围的扩大,尤其在函数项级数的讨论中,这个从面积引出的定义使用并不方便,并且可积条件过于严苛,限制了讨论范围(比如函数项级数中的一致收敛)。相信大家对积分都有过这样一个直观“定义”:它是无数长度为\(f(x)\)的线段的堆叠。这一个不严谨的印象和黎曼积分非常相似,但却有着更宽广的想象空间,因为堆叠的面积与线段的顺序无关(这是合理的假定),从而不必像黎曼积分那样关心\(f(x_0)\)领域的值。更合理的计算面积的方法应该是:把长度差不多的线段放在一起,长度乘以这些线段的“厚度”就得到一片面积,最后再累加这些面积。
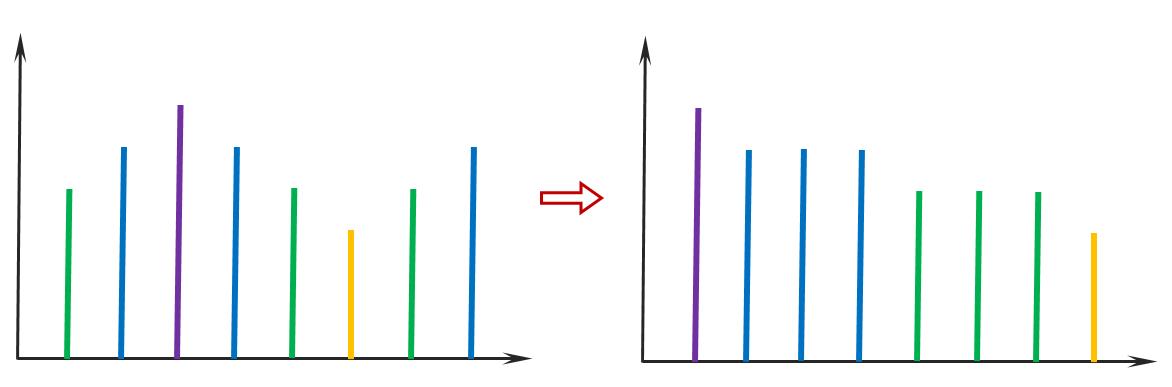
因为起初就把长度相近的放在一起,在极限意义下累积的误差一定趋于零(同黎曼积分的论证),而在此过程中我们完全不必讨论\(f(x_0)\)的领域。这样朴素的想法,如何用严谨的数学语言描述呢?有了黎曼积分的基础,其实也不难:将函数的值域分割成若干小区间\([y_i,y_i+\Delta_i)\),计算每段区间原象的“长度”\(m_i\),面积有近似值\(\Sigma_i y_im_i\),\(\Delta_i\to 0\)时的极限值就是积分。看样子要大功告成了,但其实这样的描述离“严谨”还有相当的距离。首先区间的原象可能是很复杂的点集,如何定义它们的长度?其次定义中隐含要求了,对任意的区间分割,原象的长度要都能被定义,也就是要定义“可积函数”。最后还要讨论这种积分的计算和性质,以及它和黎曼积分的关系。
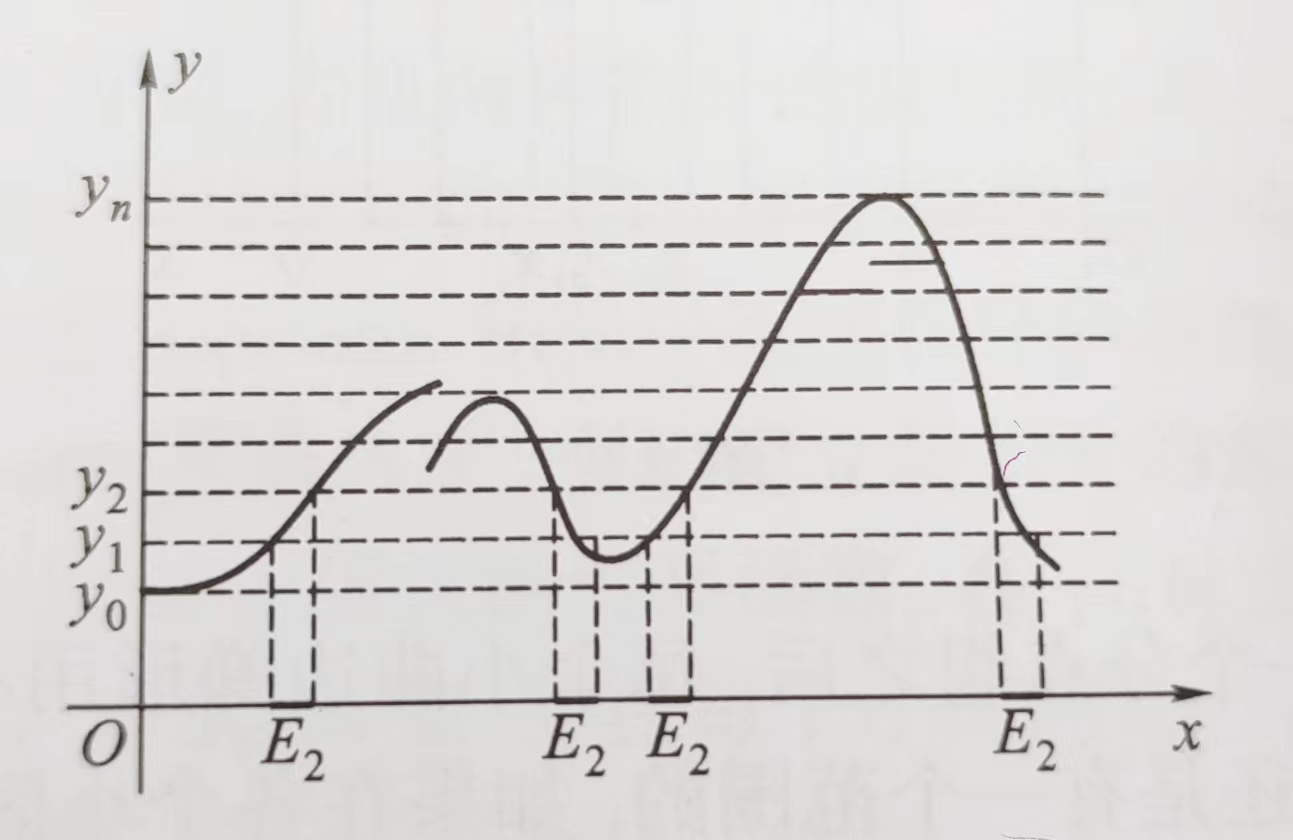
勒贝格(Lebesgue)积分就提供了一套上述问题的完整方案(勒贝格测度、勒贝格可积函数、勒贝格积分的性质),这也将是《实变函数》或《实分析》的主要内容。所以到这里我们就知道了实变函数的主要目标,它是基于测度理论的积分理论,是对传统积分的一种扩展定义,有着更好的性质和更广泛的应用场景。下一篇我们将详细讨论测度,由于要使用到复杂的集合(尤其实数集)及其度量,这里有必要补充一些集合与欧氏空间的结论(更基础的知识请移步《集合论》和《实数系统》)。
2. 集合补充
首先,测度论是要对全集的某些子集建立度量,这种度量既要满足一般的运算律(交或并),又要能兼容简单子集。比较自然的想法是从简单子集生成复杂子集,而有限次运算得到的仍然是简单子集,太过复杂的无限运算又难成理论,最值得讨论的就是可列无限次运算(式(1)中最左和最右)。使用数学归纳法,可列交和可列并(如果极限存在)有很多有限次运算的性质,而且又能产生足够复杂的子集,它们将是测度论的关键思想。
\[\bigcap_{n=1}^\infty A_n\subseteq\underset{n\to\infty}{\underline\lim}A_n\subseteq\underset{n\to\infty}{\overline\lim}A_n\subseteq\bigcup_{n=1}^\infty A_n\tag{1}\]
可列交和可列并的组合叫上限集(式(2))、下限集(式(3)),它们也是测度论中比较重要的集合。直观地讲,上限集由出现在无数个\(\{A_n\}\)中的点组成,下限集由终将一直出现在\(\{A_n\}\)后续集中的点组成,它们显然有式(1)的包含关系。当上限集和下限集都存在且相等时,就说集列\(\{A_n\}\)收敛,单调集列是典型的收敛集列(式(4,5))。
\[\underset{n\to\infty}{\overline\lim}A_n=\bigcap_{n=1}^\infty\bigcup_{m=n}^\infty A_m\tag{2}\]
\[\underset{n\to\infty}{\underline\lim}A_n=\bigcup_{n=1}^\infty\bigcap_{m=n}^\infty A_m\tag{3}\]
\[A_n\subseteq A_{n+1}\;\Rightarrow\;\lim_{n\to\infty}A_n=\bigcup_{n=1}^\infty A_n\tag{4}\]
\[A_n\supseteq A_{n+1}\;\Rightarrow\;\lim_{n\to\infty}A_n=\bigcap_{n=1}^\infty A_n\tag{5}\]
3. 欧氏空间补充
欧氏空间定义了点与点之间的距离,在这样特定的集合上(也是最常用的集合),按点之间的距离关系,可以分类出很多特殊的子集(数集)。有些集合的复杂程度甚至超出了直觉的理解,只能用定义和特征来描述,它们是抽象思维的绝好素材。需要提醒的是,以下讨论如无特殊说明,是针对一般欧氏空间的(可以是多维)。
对于给定的点集\(G\)以及点\(x_0\)(\(x_0\)不一定属于\(G\)),\(x_0\)与\(G\)的距离关系,可以简单分为3大类:(1)\(x_0\)的\(\varepsilon-\)领域都在\(A\)中,这时\(x_0\)称为\(A\)的内点;(2)\(x_0\)的任何\(\varepsilon-\)领域内都有\(A\)的点(不包含\(x_0\)),这样的\(x_0\)称为\(A\)的极限点;(3)\(x_0\)的某个\(\varepsilon-\)领域内没有\(A\)的点,\(x_0\)就叫\(A\)的孤立点。基于这3种关系,下面来定义几个特殊的点集。
先从内点的角度看,如果\(A\)的所有点都是内点,则它称为开集。空集和整个欧氏空间都是开集,还容易证明:任意一族开集的并、有限开集的交都还是开集。在直线上(一维欧式空间),开区间\((a,b)\)(可以是\(\infty\))、以及可列个不相交开区间的并,都是开集。反之对于直线上的一般开集\(A\)先证明任何点都属于一个构成区间(所有内点属于而端点不属于\(A\)的开集),再根据有理数的可列性,得到直线上的开集总是由有限或可列个不相交的开区间组成。结论看似很简单,但提醒你考虑一下有理数的分布,这些构成区间在直线上也绝不是“一字排开”那么简单的。
从极限点的角度,有3个不同的定义集合的思路,现在一一说来。首先如果\(A\)的极限点都在\(A\)中,它被称为闭集,而任意集合\(A\)添加极限点后称为闭包\(\bar{A}\),容易证明闭包也是闭集(想一下)。类似地有,空集和整个欧氏空间都是闭集,任意一族闭集的交、有限闭集的并都还是闭集。另外比较有意思的是,闭集和开集有着紧密的内在联系。通过反证法能得到:\(A\)为闭集的充要条件是补集\(E-A\)为开集,或者说闭集的补集是开集、开集的补集是闭集。从而直线上的闭集总可以通过挖去有限或可列个不相交的开区间构成,注意这里并没有说由闭区间组成,同样是因为开集构成区间的复杂布局。
• 求证:\(\{\cos n\}\)的闭包是\([-1,1]\)。
第2种思路,如果\(A\)中点都是极限点,则\(A\)称为自密集。更特殊地,既是自密又封闭(注意两者的差异)的集称为完全集(自密闭集)。自密集中没有孤立点,从而直线上的完全集是这样的闭集:它的补集没有相邻的构成区间。
最后第3种思路,研究\(A\)的极限点集\(A'\)与另一个集合\(B\)的关系。如果\(B\subseteq A'\),则称\(A\)在\(B\)中稠密,它表示\(B\)中的点总是被\(A\)“包围”。当然,一般在连续的空间中,才更能体现出“稠密”的字面意思。为此一般把整个欧氏空间选作\(B\),这时的\(A\)被称为稠密集。相反地,如果\(A'\)不包含非零开集,它就叫无处稠密集或疏朗集(注意强调的是开区间)。疏朗集中自然不能包含任何非空开集,不包含非空开集的闭集(必须是闭集)也一定是疏朗集。另外,如果\(A'\)不包含整个空间,其余集必包含非空开集,使用反证法可知,疏朗集的余集一定是稠密集,稠密集的余集如果是闭集也一定是疏朗集(自行证明)。
直观上讲,完全集的点很“密集”,疏朗集很“稀疏”,然而这里的“密集”描述的是离散点,“稀疏”强调的则是连续性,所以他们并不对立,甚至是可以并存的。原本有理数是阐述这种“密集”和“稀疏”的绝好素材,无耐它不是闭集,这使得它与完全集和疏朗集都无缘。但其实只要对它稍作修改,就可以两个条件都满足,我们下面就来构造这样的集合。
抓住两种集合的核心特征,完全集的补集没有相邻的构成区间,疏朗闭集不能连城片。不妨在\([0,1]\)上(直线也可以先分割为无数个线段)考虑这样的集合:先挖去中间的\([\dfrac{1}{3},\dfrac{2}{3}]\),然后在剩下的两段上持续挖去中间的\(\dfrac{1}{3}\)开区间。这个集合\(C\)的余集是可列个互不相交的开区间,所以\(C\)是闭集;另外这些开区间都不相邻,所以\(C\)是完全集。最后由于会被一直挖下去,\(C\)不会包含任何非空开集(开集有长度),所以\(C\)又是疏朗集。
这个集合就是康托尔集,根据构造过程不难发现,它其实是三进制小数中只有0和2表达的小数(注意\(0.1=0.0\dot{2}\)),当然你也可以模仿构造十进制小数的康托尔集。比较有意思的是,康托尔集被挖去的部分,总长度正好是1,也就是说在一个合理的测度定义下,康托尔集的测度是0!然而它却又与实数集是等势的(考虑实数的二进制表示),这就说明等势的两个集合测度未必都大于0或等于0。

【前序学科】集合论、实数系统、微积分
【参考资料】
[1] 《实变函数论和泛函分析(上)》,夏道行,2010
本博客的主要参考课本,教材从直接从一般的测度讲起,穿插讲述Lebesgue测度,使得理论更通用更系统。
[2] 《实变函数论》,周民强,2016
国内难得的一本经典教材,以欧氏空间的Lebesgue测度为对象,内容丰富全面、穿插历史典故,可做教材或查阅资料。
[3] 《陶哲轩实分析》,陶哲轩,2008
从零开始学习分析学,完整阐述了数系、集合、函数、度量、测度等基本概念,使读者建立起严谨的数学意识,为深入学习分析学打好基础。




 浙公网安备 33010602011771号
浙公网安备 33010602011771号