题解：P6782 [Ynoi2008] rplexq

更差的阅读体验

---

假设树的点数为 \(n\)，询问数量为 \(q\)。

首先考虑一个复杂度和度数有关的做法。

这个是比较简单的。假设一个广义的 \(sz_u\) 表示一次询问的时候 \(u\) 子树在 \([l, r]\) 的点数。那么一次询问的答案就是，\(u\) 子树内的点对数量，减去 \(u\) 每个儿子子树的点对数量，即

\[{sz_u \choose 2} - \sum_{v \isin son_u} {sz_v \choose 2} \]

至于 \(sz_u\) 怎么求，可以扔到二维平面上。一个点 \(i\) 的坐标有两维，为 \((i, dfn_i)\)。由于在一个子树内的点 \(dfn\) 是一个区间，又因为我们查询的节点编号也是一个区间，所以是一个矩形数点。我们可以离线把每个子树的查询离线下来，扫描线。

我们对度数根号分治。假设阈值 \(B\)，我们对度数 \(\le B\) 的结点做上面那个过程。然后我们发现我们有 \(O(n)\) 个点，但是有 \(O(nB)\) 次查询，所以我们可以用一个 \(O(\sqrt n)\) 修改 \(O(1)\) 查询的分块来平衡复杂度。

这一部分在 \(O(nB + n \sqrt n)\) 的时间内得到解决。

接下来考虑度数 \(> B\) 的点。我们把 \(u\) 的每个子树内的点分别染成一种颜色，如图。

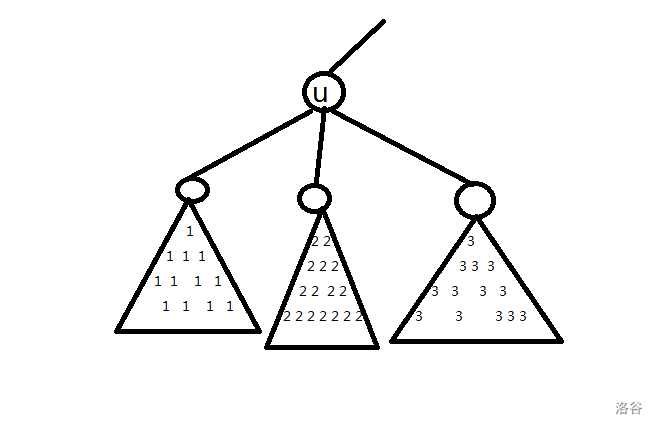
发现 LCA 为 \(u\) 的点对，就是颜色不同的点对数量！求颜色不同的点对数量，我们可以用总数减去颜色相同的点对数量得到。

看起来比较对的一个做法就是莫队。这样度数大的点数量不会超过 \(\frac{n}{B}\) 个。假设我们现在正在处理点 \(u\)，那么我们对它的每一个子树染色，把这个 \(u\) 的所有询问做一个莫队，数同色数对个个数，单次可以做到莫队的复杂度也就是 \(O(n \sqrt q)\)。

到这里我们发现寄完了。因为 \(n\) 是在根号外面，如果对每个度数 \(>B\) 的点都做一遍的话那么复杂度就变成 \(O(\frac{n^2 \sqrt q}{B})\)。由于莫队的总点数没有保证，所以直接莫队的复杂度是错的。

但是我们发现，我们可以把大度点的前 \(B\) 大的子树拎出来去做上面的二维数点过程，剩下的子树莫队，就对了。

考虑证明这个事情。假设一个点与它前 \(B\) 大的子树的根的连边是重边，其余边是轻边。前 \(B\) 大子树的根是重儿子，其余是轻儿子。

对于一个大小为 \(sz_u\) 的子树 \(u\)（这里 \(sz\) 和上面 \(sz\) 的意思不一样，这里指的就是子树内的点数），假如它是一个轻儿子，那么它父亲的子树大小至少是 \(O(B sz_u)\)。所以我们从一个点往上跳 \(x\) 次轻边，子树大小至少是 \(O(B^x)\)，容易发现在 \(B\) 取得恰当的时候，\(x = O(1)\)，也就是一个点只会被莫队处理 \(O(1)\) 次。

这样莫队的总点数就是 \(O(n)\) 了！

到这里我们可能会发现，一开始对度数进行根号分治已经不必要了。我们可以直接取阈值 \(B\)，然后假设点 \(u\) 的儿子数量为 \(deg_u\)，那么我们直接取它前 \(\min(deg_u, B)\) 的子树进行二维数点，如果还有剩下的子树，我们再跑莫队。

至此，问题在 \(O(n \sqrt n + q \sqrt n + n \sqrt q)\) 的时间内得到解决。

---

在实现中，我们发现，我们 \(O(\sqrt n) - O(1)\) 的分块中的根号跑的是极其满的，而我们莫队的常数看起来非常小。所以我们可以把 \(B\) 取小一点，少跑几次分块，多跑几次莫队，这样就很快。

实际操作中 \(B = 3\)，太疯狂了。由于我们的 \(B\) 很小，我们甚至可以直接开 \(O(nB)\) 的空间，就没有被卡空间的问题了。

#include<bits/stdc++.h>
#define endl '\n'
#define N 500006
#define M 5006
using namespace std;
using i64=long long;
int n,B,q,rt,bn,b[N],co[N],dfs_clock,f[N],dfn[N],sz[N],sum[N][4],c[N];
i64 ans[N],cnt;
vector<int> G[N],t[N]; vector<pair<int,int> > vec[N];
struct Ask {int l,r,u;} ask[N];
bool operator <(Ask x,Ask y)
{
    int blx=(x.l-1)/B+1,bly=(y.l-1)/B+1;
    return blx!=bly?blx<bly:(blx&1?x.r<y.r:x.r>y.r);
}
struct Block {
    int tag[M],val[N];
    void update(int l,int r,int x)
    {
        int bl=(l-1)/B+1,br=(r-1)/B+1;
        if(bl==br){for(int i=l;i<=r;i++)val[i]+=x; return;}
        int rb_l=min(n,bl*B),lb_r=(br-1)*B+1;
        for(int i=bl+1;i<br;i++)tag[i]+=x;
        for(int i=l;i<=rb_l;i++)val[i]+=x;
        for(int i=lb_r;i<=r;i++)val[i]+=x;
    }
    int query(int k){return val[k]+tag[(k-1)/B+1];}
    inline void update(int k,int x){update(k,n,x);}
    inline int query(int l,int r){return query(r)-query(l-1);}
} ds;
void dfs1(int u,int fa)
{
    sz[u]=1,f[u]=fa; vector<int> son;
    for(int v:G[u])if(v!=fa)dfs1(v,u),sz[u]+=sz[v],son.push_back(v);
    sort(son.begin(),son.end(),[](int x,int y) {
         return sz[x]>sz[y];
    });
    G[u].swap(son);
}
void dfs2(int u){dfn[u]=++dfs_clock; for(int v:G[u])dfs2(v);}
void dfs3(int u,int col){b[++bn]=u,co[u]=col; for(int v:G[u])dfs3(v,col);}
inline i64 binom2(int x){return 1ll*x*(x-1)/2;}
inline int calc(int u){return ds.query(dfn[u],dfn[u]+sz[u]-1);}
inline void mo_add(int x){if(x)cnt+=c[x]++;}
inline void mo_del(int x){if(x)cnt-=--c[x];}
void solve_small()
{
    for(int i=1;i<=n;i++)
    {
        ds.update(dfn[i],1);
        for(auto [j,opt]:vec[i])
        {
            int u=ask[j].u,sz=G[u].size(); ans[j]+=opt*calc(u);
            for(int k=0;k<3&&k<sz;k++)sum[j][k]+=opt*calc(G[u][k]);
        }
    }
    for(int i=1;i<=q;i++)
    {
        ans[i]=binom2(ans[i]); int sz=G[ask[i].u].size();
        for(int j=0;j<3&&j<sz;j++)ans[i]-=binom2(sum[i][j]);
    }
}
void solve_big()
{
    for(int i=1;i<=q;i++)
        if(G[ask[i].u].size()>3)t[ask[i].u].push_back(i);
    for(int u=1;u<=n;u++)if(t[u].size())
    {
        bn=0; int sz=G[u].size();
        for(int i=3;i<sz;i++)dfs3(G[u][i],G[u][i]);
        sort(b+1,b+1+bn);
        for(int i:t[u])
        {
            auto &[l,r,_]=ask[i];
            l=lower_bound(b+1,b+1+bn,l)-b,r=upper_bound(b+1,b+1+bn,r)-b-1;
        }
        sort(t[u].begin(),t[u].end(),[](int x,int y) {
             return ask[x]<ask[y];
        }),cnt=0; int lb=1,rb=0;
        for(int i:t[u])
        {
            auto [l,r,_]=ask[i];
            for(;lb>l;mo_add(co[b[--lb]])); for(;lb<l;mo_del(co[b[lb++]]));
            for(;rb<r;mo_add(co[b[++rb]])); for(;rb>r;mo_del(co[b[rb--]]));
            ans[i]-=cnt;
        }
    }
}
main()
{
    scanf("%d%d%d",&n,&q,&rt),B=pow(n,0.5);
    for(int i=1,u,v;i<n;i++)
        scanf("%d%d",&u,&v),G[u].push_back(v),G[v].push_back(u);
    dfs1(rt,0),dfs2(rt);
    for(int i=1;i<=q;i++)
        scanf("%d%d%d",&ask[i].l,&ask[i].r,&ask[i].u),
        vec[ask[i].l-1].push_back({i,-1}),vec[ask[i].r].push_back({i,1});
    solve_small(),solve_big();
    for(int i=1;i<=q;i++)printf("%lld\n",ans[i]);
    return 0;
}