题解：P11425 [清华集训 2024] 路南柯

更差的阅读体验

---

深刻啊。

这个拓扑序看着很奇怪，我们把它变成一个我们熟悉的东西，dfs 序。注意到把 dfs 序 reverse 一下就可以得到一个剥叶子的序列。所以接下来构造的都是 dfs 序，最后倒着输出就可以。

首先考虑菊花的情况，因为这个情况可能给我们后续的讨论捣乱。假设以 \(1\) 为根，那么显然一个排列确定不了这棵树，所以两个排列就是最优的了。我们构造 \(\{1, 2, 3, \cdots, n\}\)，还有 \(\{1, n, n-1, \cdots, 2\}\)，那么由这两个排列我们可以知道 \(2 \sim n\) 两两不存在父子关系，所以一定都是 \(1\) 的儿子。我们就构造好了。

对于一般树，我们发现这个 dfs 序有用的性质也不多，也就是一个点的父亲一定在这个点前面出现。

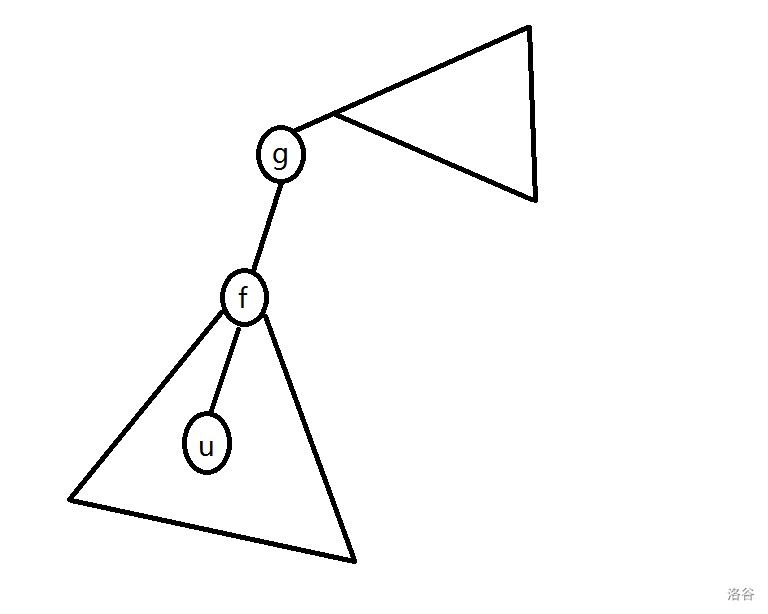
考虑图示情况，我们希望分辨结点 \(u\) 的父亲 \(f\) 和爷爷 \(g\)。我们需要找到一个根开始 dfs。

不难发现，如果根在 \(g\) 子树外，那么一定是先遍历到 \(g\) 再遍历到 \(u\)；如果在 \(f\) 子树内，那么一定是先遍历到 \(f\) 再遍历到 \(g\)。那么如果我们可以在两个区域内各自选择一个点开始跑 dfs，就可以从遍历顺序相反的一对点中找到这一对父子。

考虑极端情况：我们希望分辨一个叶子和他的父亲。那么我们要从叶子的父亲子树之外选点 dfs，也要从叶子本身开始选点 dfs。有个很显然的事情，那就是对于每个点子树内和子树外一定都有叶子。所以我们可以直接从每个叶子开始 dfs，记录下 dfs 序输出。

然而这不是最优的。我们发现分辨叶子和父亲其实不需要对每个叶子进行 dfs。

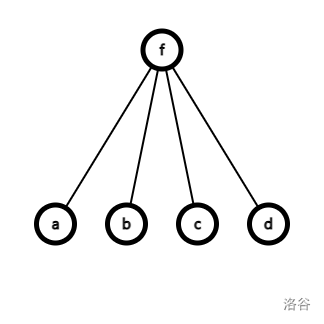
发现这个局部长得很像一个菊花。所以我们可以在这里沿用菊花的做法，就是我们不分别从 \(a, b, c, d\) 开始 dfs，而是只从 \(f\) 开始 dfs 一遍。但是这样就无法分辨 \(a, b, c, d\) 和 \(f\) 的父亲。根据菊花的做法，我们可以在第一次遍历到 \(f\) 的时候以 \(a, b, c, d\) 的顺序遍历其儿子，第二次遍历的时候就以 \(d, c, b, a\) 的顺序遍历其儿子。这样 \(a, b, c, d\) 必没有父子关系，都是 \(f\) 的儿子。如此就可以分辨了。

答案就是叶子的父亲个数。为啥这个是答案下界呢？因为如果对于一个叶子，它不选，它的父亲也不选，那么永远无法分辨它和它父亲了。

按照如上方法构造，复杂度 \(O(n^2)\)。

#include<bits/stdc++.h>
#define endl '\n'
#define N 106
using namespace std;
int n,ans,ord[N],vis[N],dfs_clock; vector<int> G[N];
void dfs(int u,int fa,int rt)
{
	ord[++dfs_clock]=u; vector<int> leaf;
	for(int v:G[u])
		if(v!=fa&&G[v].size()==1)leaf.push_back(v);
	if(vis[u])reverse(leaf.begin(),leaf.end()); vis[u]=1;
	for(int v:leaf)ord[++dfs_clock]=v;
	for(int v:G[u])
		if(v!=fa&&G[v].size()>1)dfs(v,u,rt);
}
void solve()
{
	scanf("%d",&n),ans=0;
	for(int i=1;i<=n;i++)G[i].clear(),vis[i]=0;
	for(int i=1,u,v;i<n;i++)
		scanf("%d%d",&u,&v),G[u].push_back(v),G[v].push_back(u);
	for(int i=1;i<=n;i++)if(G[i].size()==n-1)
	{
		printf("2\n");
		for(int j=1;j<=n;j++)if(j!=i)printf("%d ",j);
		printf("%d\n",i);
		for(int j=n;j;j--)if(j!=i)printf("%d ",j);
		return printf("%d\n",i),(void)0;
	}
	for(int i=1;i<=n;i++)if(G[i].size()>1)
	{
		int cnt=0;
		for(int j:G[i])if(G[j].size()>1)cnt++;
		ans+=(cnt==1);
	}
	printf("%d\n",ans);
	for(int i=1;i<=n;i++)if(G[i].size()>1)
	{
		int cnt=0;
		for(int j:G[i])if(G[j].size()>1)cnt++;
		if(cnt^1)continue; dfs_clock=0,dfs(i,0,i);
		for(int j=n;j;j--)printf("%d%c",ord[j]," \n"[j==1]);
	}
}
main()
{
	int T; scanf("%d",&T);
	while(T--)solve();
	return 0;
}