从经典动力学理解勒让德变换

技术背景

勒让德变换在经典力学和统计力学中是非常常用的一个数学工具，其变换了一个函数的所有（或部分）自变量，也改变了函数的形式，最终却不改变函数所表征的意义。最典型的案例是从拉格朗日动力学到哈密顿动力学的勒让德变换的应用，最终证明了两种力学框架的一致性。但是勒让德变换作为一个数学工具，光看形式的话很容易让人不明所以，这里我们代入一个经典动力学的案例，来看看勒让德变换的真实物理含义是什么。

场景假设

假定某一个白天，勒让德正在一个操场上自南向北走过，突然他向右一转头，发现一个自东向西飞过来的足球，砸中了自己的脑袋。勒让德并没有看清楚球的具体轨迹，但是离勒让德不远的足球场上正站着三个人，一个人在勒让德的正东方，一个人在勒让德的东南方，一个人在勒让德的东北方。那么问题来了，是谁踢中了勒让德的脑袋呢？此时勒让德想起来球在砸到你的脑袋的一瞬间，是自东向西飞的，于是勒让德笃定就是在正东方的那个人踢过来的球【后人称之为勒让德变换】，然后勒让德跑过去把他打了一顿。但是勒让德不仅没打得过他，还被告知自己找错人了，这是怎么一回事呢？

动力学与勒让德变换

我们首先给定一个经典动力学中的直线匀速运动方程：

\[s(t)=vt+s_0 \]

其中\(s(t)\)为\(t\)时刻的位置，\(s_0\)为\(t=0\)时刻的位置，\(v\)表示速度，并且是一个常量。则该方程的全微分形式为：

\[ds=vdt \]

而此时我们看着等式右边的表达式，想到了\(vdt\)可能是另外一个全微分形式的一部分：\(d(vt)=vdt+tdv\)，将这个全微分形式移项再代入到上述的全微分表达式中有：

\[ds=d(vt)-tdv\\ d(vt-s)=tdv \]

则，令函数\(g(v)=vt-s\)就称之为\(s(t)\)的勒让德变换，需要注意的有：\(\frac{\partial g}{\partial v}=t\)。类似的道理，我们也可以对\(g(v)\)再度做勒让德变换：

\[dg=tdv=d(vt)-vdt\\ d(vt-g)=vdt \]

于是我们发现，\(s=vt-g\)又变回来了，因此\(s(t)\)和\(g(v)\)互为勒让德变换。那么在这种假定的前提条件下，上一个章节的场景假设中，勒让德应该没打错人，那是怎么一回事呢？我们考虑一个马格努斯力的场景：在流体中运动的球体，如果本身带有自旋，会受到一个前进速度与角速度平面法向的作用力，称之为马格努斯力，其形式为：

\[F=\frac{4}{3}(4\pi^2r^3\rho\omega v) \]

其中\(r\)是球体半径，\(\rho\)是空气密度，\(\omega\)是球体自旋的角速度，\(v\)是球体前进的速度。相关的马格努力作用下的球体轨迹如下图所示：

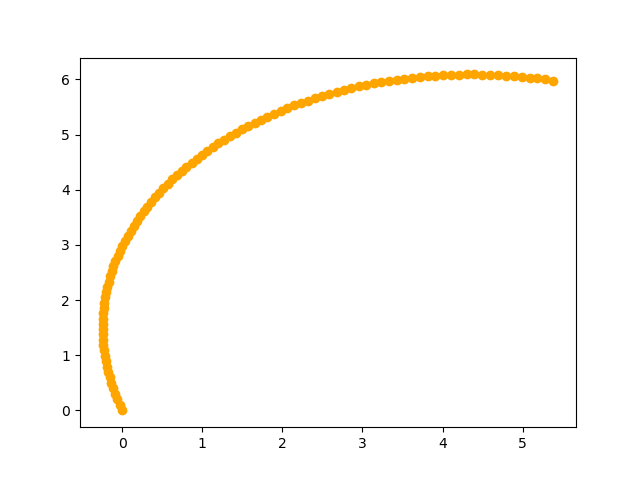
因此马格努斯力对球体直线运动造成的偏移量为：

\[s(t)=vt+s_0+\frac{8}{3m}\pi^2r^3\rho\omega vt^2 \]

全微分形式变成了：

\[ds=vdt+\frac{16}{3m}\pi^2r^3\rho\omega vtdt=vdt+a(v)tdt \]

这里为了简写，假定了一个新的函数\(a(v)=\frac{16}{3m}\pi^2r^3\rho\omega v\)，那么代入以下的两个变换：

\[vdt=d(vt)-tdv\\ atdt=d(\frac{1}{2}at^2)-\frac{1}{2}t^2da \]

就可以得到：

\[ds=d(vt)-tdv+d(\frac{1}{2}at^2)-\frac{1}{2}t^2da\\ d(vt+\frac{1}{2}at^2-s)=tdv+\frac{1}{2}t^2da \]

新的勒让德变换函数为：\(g^*(v)=vt+\frac{8}{3m}\pi^2r^3\rho\omega vt^2-s\neq vt-s=g(v)\)。通过这两个变换，我们逐渐发现了勒让德变换在这个案例中的物理含义：每一个时间点\(\tau\)都会有一个对应的矢量速度\(v_{\tau}\)，由于\(s(t)\)是连续函数，因此我们可以假设\(\tau+\delta t\)的小量时间内做匀速直线运动，那么勒让德变换就是一个扩展的假设，把整段\([0,\tau+\delta t]\)时间内的运动看做是匀速直线运动。不论是\(g^*(v)\)还是\(g(v)\)，都有：

\[s^*(t)=(v_{\tau}+\frac{16}{3m}\pi^2r^3\rho\omega v_{\tau}\tau)t-g^*(v_{\tau}) \]

这个公式所表示的是\(s(t)\approx s^*(t),t\in[0,\tau+\delta t]\)，而\(g^*(v_{\tau})=s^*(0)\)，即：勒让德变换表示的是在\(\tau\)时刻的球体轨迹切线方程在\(t=0\)时刻的值\(s^*(0)\)，也就是勒让德以为的肇事者所在的位置，而实际上真正的肇事者在\(g^*(v_0)=s(0)\neq s^*(0)\)，这就是勒让德找错肇事者的原因。而上一个章节中，只有在踢出来的球没有侧旋，即表达式中的\(\omega=0\)时，运动轨迹变成了一个匀速直线运动（即：\(s_{\omega=0}(0)=s^*_{\omega=0}(0)\)），此时勒让德对肇事者的判断才是准确的。

可能看到这里还是会有人对于勒让德变换的物理含义表示不解，这里再做一下简单总结：勒让德变换在动力学过程中表示物体近似运动过程的出发点，对于凸函数，只有在初始的时刻才有勒让德变换的函数值与物体真实运动过程的出发点重合。

勒让德变换图像

如下图片来自于参考链接3，用\(y^*=f'(x_0)x-f^*\)的形式近似\(y=f(x)\)在\(x_0\)处的值，其中对应的\(x=0\)处的\(y^*\)的值\(f^*\)就是勒让德变换的函数值：

下图来自于参考链接1，其表述的内容与上图一致，但是需要注意的是，对于每一个函数\(y=f(x)\)的点，都有一个对应的勒让德变换的函数值，新的自变量与这些函数值共同构成了勒让德变换的函数形式：

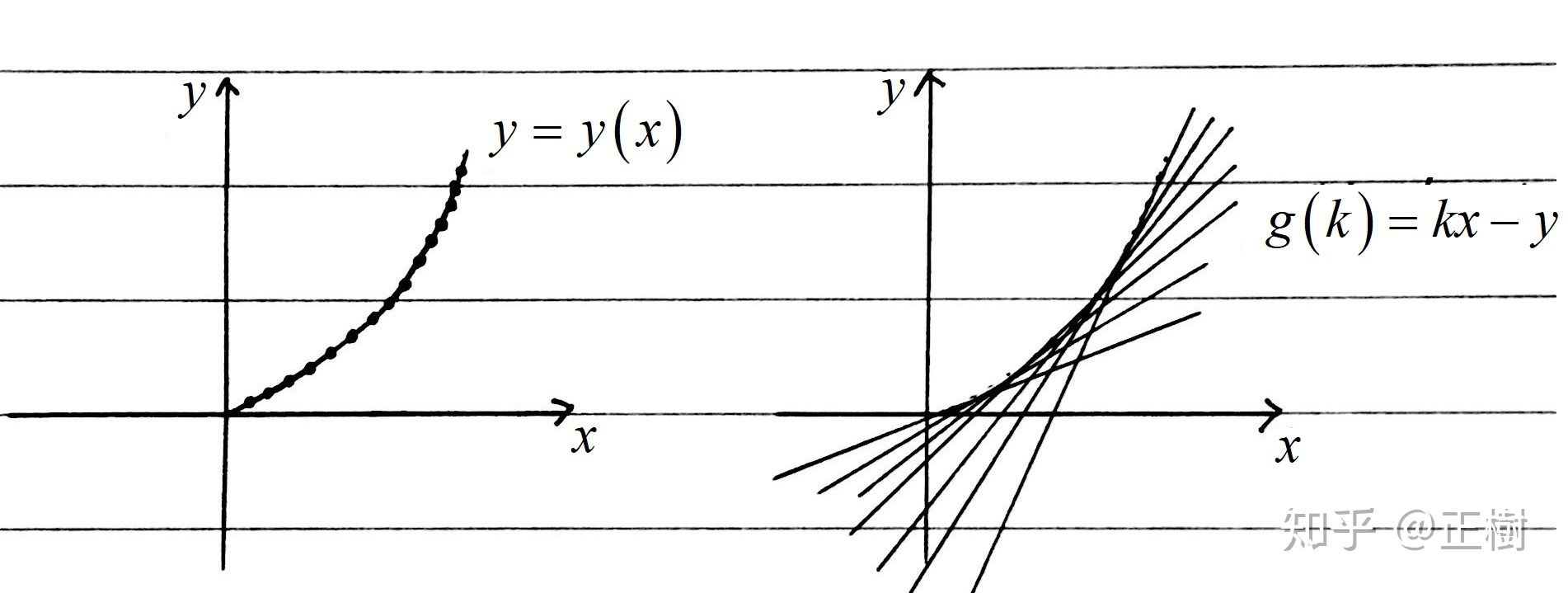
多变量勒让德变换

上述的案例主要是针对单变量和双变量的特殊勒让德变换的形式进行讲解，这里我们把勒让德变换写成更加一般的多变量形式，首先给定一个多变量函数\(f(x_1,x_2,...,x_n)\)的全微分形式：

\[df=\sum_{i=1}^n\frac{\partial f}{\partial x_i}dx_i=\sum_{i=1}^ny_idx_i \]

然后将\(y_idx_i=d(y_ix_i)-x_idy_i\)代入，得到：

\[df=d\left(\sum_{i=1}^ny_ix_i\right)-\sum_{i=1}^nx_idy_i\\ d\left(-f+\sum_{i=1}^ny_ix_i\right)=\sum_{i=1}^nx_idy_i \]

则函数\(g=-f+\sum_{i=1}^ny_ix_i\)称为函数\(f\)的勒让德变换，并且，勒让德变换还具备如下的关系：

\[\frac{\partial g}{\partial y_i}=x_i \]

以上就是勒让德变换的多变量形式，变换本身并不是很复杂，重点关注一下在具体问题中的应用。

拉格朗日力学与哈密顿力学

在拉格朗日力学中，我们一般用广义坐标\(q\)和广义速度\(\dot{q}\)来表征物体的动力学状态，对于每一个系统，动力学过程可以用拉格朗日量\(L(q,\dot{q},t)=T-V\)来描述，其中\(T\)表示系统动能，\(V\)表示系统势能。根据保守系的欧拉-拉格朗日方程有：

\[\frac{\partial L}{\partial q}=\frac{d}{dt}\frac{\partial L}{\partial \dot{q}} \]

由于拉格朗日量中只有动能项显含广义速度，因此可以得到一个新的参数，系统动量\(p\)与\(q\)的相互关系（此时注意我们的目标是把\((q,\dot{q})\)的表象变换到\((p,q)\)的表象）:

\[p=\frac{\partial L}{\partial \dot{q}},\dot{p}=\frac{\partial L}{\partial q} \]

则可得到拉格朗日量的全微分形式：

\[\begin{align*} dL&=\frac{\partial L}{\partial q}dq+\frac{\partial L}{\partial \dot{q}}d\dot{q}+\frac{\partial L}{\partial t}dt\\ &=\dot{p}dq+pd\dot{q}+\frac{\partial L}{\partial t}dt\\ &=\dot{p}dq+d(p\dot{q})-\dot{q}dp+\frac{\partial L}{\partial t}dt \end{align*} \]

等式左右交替位置，整理可得：

\[dH=d(p\dot{q}-L)=\dot{q}dp-\dot{p}dq-\frac{\partial L}{\partial t}dt \]

其中\(H=p\dot{q}-L\)是拉格朗日量的一个勒让德变换，也被称为哈密顿量。同时由该哈密顿量，可以推导出哈密顿-正则运动方程：

\[\frac{\partial H}{\partial p}=\frac{dq}{dt}\\ \frac{\partial H}{\partial q}=-\frac{\partial L}{\partial q}=-\frac{dp}{dt} \]

同时，我们也可以通过勒让德变换的函数形式推断出哈密顿量的物理含义：\(H=p\dot{q}-L=T+V\)，也就表示着系统总能量。就这样通过勒让德变换，就可以证明拉格朗日力学跟哈密顿力学的等价性。

勒让德变换与统计力学

热力学的基本方程，是内能的全微分：

\[dU=-PdV+TdS \]

代入\(PdV=d(PV)-VdP\)做勒让德变换得：

\[dU=VdP-d(PV)+TdS\\ dH=d(U+PV)=VdP+TdS \]

其中\(H=U+PV\)是热力学焓。类似的方法，对内能全微分代入\(TdS=d(TS)-SdT\)做勒让德变换得：

\[dU=-PdV+d(TS)-SdT\\ dF=d(U-TS)=-PdV-SdT \]

其中\(F=U-TS\)是亥姆赫兹自由能。接下来对焓的全微分代入\(TdS=d(TS)-SdT\)做勒让德变换得：

\[dH=VdP+d(TS)-SdT\\ dG=d(H-TS)=VdP-SdT \]

其中\(G=H-TS=U+PV-TS\)是热力学系统的吉布斯自由能。并且由上述的四个\(U,H,F,G\)的表达式，可以推导出麦克斯韦关系式：

\[dU=-PdV+TdS=\frac{\partial U}{\partial V}dV+\frac{\partial U}{\partial S}dS\\ T=\frac{\partial U}{\partial S},P=-\frac{\partial U}{\partial V}\\ \frac{\partial T}{\partial V}=\frac{\partial^2 U}{\partial S\partial V}=-\frac{\partial P}{\partial S} \]

同理可以计算得：

\[\frac{\partial T}{\partial P}=\frac{\partial V}{\partial S}\\ \frac{\partial S}{\partial V}=\frac{\partial P}{\partial T}\\ \frac{\partial S}{\partial P}=-\frac{\partial V}{\partial T} \]

这样，就可以通过勒让德变换，从热力学基本方程推导到麦克斯韦关系式。

总结概要

为了通过一些实际问题来理解勒让德变换，我们假定了这样的一个场景：一个叫勒让德的人在足球场边上被不知来源的球砸中了脑袋，只能够判断足球砸到脑袋的一瞬间的速度方向。而通过勒让德变换的函数值，结合足球旋转的角速度，我们就可以得出足球的真实来源。同时，通过勒让德变换，我们还可以从拉格朗日力学推导到哈密顿力学。而且勒让德变换在热力学系统也有非常重要的应用场景。