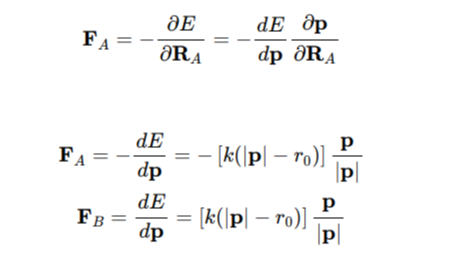
本文通过一个简单的微分计算,说明了为什么弹簧对两头的作用力方向总是沿着弹簧方向的。虽然是一个固有的认知,但其实也可以通过简单的计算来进行论证。
问题背景
虽然这个问题听起来有点奇怪,弹簧的弹力不就应该沿着弹簧吗?——是的,没错。大家中学阶段都学过的,胡克定律,\(F=k(x-x_0)\),并且这个作用力,在拉伸状态是向内收的,挤压状态,作用力是向外的。还有弹性势能\(E=\frac{1}{2}k(x-x_0)^2\)。是的,这些都没错,但是有没有人想过为什么?这个问题,其实还得从一个简单的微分说起。
关于谐振势的微分
我们都知道力是能量对空间坐标的一个导数,例如如下形式:
\[\textbf{F}=-\frac{d E}{d \textbf{r}}
\]
那么对于一个简单的谐振子体系:
我们分析其中一个物体的受力时,有:
\[\textbf{F}_A=-\frac{\partial E}{\partial \textbf{r}_A},\textbf{F}_B=-\frac{\partial E}{\partial \textbf{r}_B}
\]
那么这里比较通用的一个势能表达式为:
\[E=\frac{1}{2}k\left[\sqrt{\left(\textbf{r}_A-\textbf{r}_B\right)^2}-r_0\right]^2
\]
可以假定一个向量\(\textbf{q}=\textbf{r}_A-\textbf{r}_B\),原式可以变换为:
\[E=\frac{1}{2}k\left[\sqrt{q_x^2+q_y^2+q_z^2}-r_0\right]^2
\]
那么就有:
\[\frac{\partial E}{\partial q_x}=k(|\textbf{q}|-r_0)\cdot\frac{1}{2}|\textbf{q}|^{-1}\cdot 2q_x=\left[k(|\textbf{q}|-r_0)\right]\frac{q_x}{|\textbf{q}|}
\]
类似的还有:
\[\frac{\partial E}{\partial q_y}=\left[k(|\textbf{q}|-r_0)\right]\frac{q_y}{|\textbf{q}|}\\
\frac{\partial E}{\partial q_z}=\left[k(|\textbf{q}|-r_0)\right]\frac{q_z}{|\textbf{q}|}
\]
那么其实,对于整个向量\(\textbf{q}\)的求导来说就是:
\[\frac{d E}{d \textbf{q}}=\left[k(|\textbf{q}|-r_0)\right]\frac{\textbf{q}}{|\textbf{q}|}
\]
该式子的前面一项是标量,表示作用力的大小,也就是胡克定律中的计算公式,后边这一项\(\frac{\textbf{q}}{|\textbf{q}|}\)表示A和B之间的单位向量。那么就可以分别去计算两个物体的作用力:
\[\textbf{F}_A=-\frac{\partial E}{\partial \textbf{R}_A}=-\frac{d E}{d \textbf{q}}\frac{\partial \textbf{q}}{\partial \textbf{R}_A}
\]
后边这个雅克比矩阵其实就是一个带正负号的单位矩阵,所以简化就是:
\[\textbf{F}_A=-\frac{d E}{d \textbf{q}}=-\left[k(|\textbf{q}|-r_0)\right]\frac{\textbf{q}}{|\textbf{q}|}\\
\textbf{F}_B=\frac{d E}{d \textbf{q}}=\left[k(|\textbf{q}|-r_0)\right]\frac{\textbf{q}}{|\textbf{q}|}
\]
此时再论证一下两个作用力的方向性问题。当\(|\textbf{q}|>r_0\)时,\(\textbf{F}_A\)是沿着\(-\textbf{q}\)的方向,\(\textbf{F}_B\)是沿着\(\textbf{q}\)的方向,也就是两个力都向内收。同样的,也可以论证在\(|\textbf{q}|<r_0\)时,两个作用力是沿着弹簧方向向外拉的。
总结概要
本文通过一个简单的微分计算,说明了为什么弹簧对两头的作用力方向总是沿着弹簧方向的。虽然是一个固有的认知,但其实也可以通过简单的计算来进行论证。
版权声明
本文首发链接为:https://www.cnblogs.com/dechinphy/p/spring-force.html
作者ID:DechinPhy
更多原著文章:https://www.cnblogs.com/dechinphy/
请博主喝咖啡:https://www.cnblogs.com/dechinphy/gallery/image/379634.html



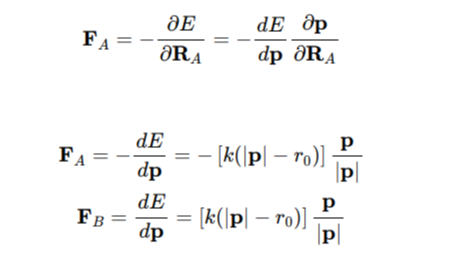 本文通过一个简单的微分计算,说明了为什么弹簧对两头的作用力方向总是沿着弹簧方向的。虽然是一个固有的认知,但其实也可以通过简单的计算来进行论证。
本文通过一个简单的微分计算,说明了为什么弹簧对两头的作用力方向总是沿着弹簧方向的。虽然是一个固有的认知,但其实也可以通过简单的计算来进行论证。

 浙公网安备 33010602011771号
浙公网安备 33010602011771号