99-Flagstone Walk

The main hall of UESTC is far from the dormitory. However, poor Hongshu has to go there every day to talk with his teachers. This is the most unhappy thing on the earth. However, Hongshu is so optimistic that he still digs a lot of fun during that boring period.

There is a long flagstone walk on the way from the dormitory to the main hall. This flagstone walk has NN lines and four flagstones arranged in each line. Hongshu always start from rightmost flagstone of the first line. In order to make this walk funny, he would always step onto the left or right flagstone in the next line if there is. For example, if Hongshu stands at the second rightmost flagstone of the third line, he would choose to step to the first or third rightmost one of the forth line. Note that Hongshu has only one choice when he is at the corner of one line.

Because Hongshu has to go to the main hall every day, he wants to know how many different ways to step across the flagstone walk. Can you help him?

Standard Input

The first line of the input is an integer T (T≤20), which stands for the number of test cases you need to solve.
Each case consists of an integer N (1≤N≤20) on a single line, which stands for the length of the walk.

Standard Output

For each case, print the number of ways on a single line.

Samples

Input	Output
3 2 3 4	1 2 3

Note

Hongshu has 33 ways to choose when the length of walk is 44.

 

 

 

 

 

 

 

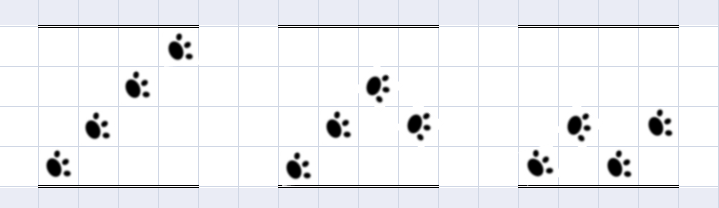
很有意思的一个题目。英文描述有问题，但看图应该能明白。最后发现是一个斐波拉契数列

#include <stdio.h>

int fib(int n);

int main() {
    setbuf(stdout, NULL);

    int T, N, result;

    scanf("%d", &T);
    while (T--) {
        scanf("%d", &N);
        result = fib(N - 1);
        printf("%d\n", result);
    }
    return 0;
}

int fib(int n) {
    int a = 1;  
    int b = 2;  
    int c = 0;  
    int i;
    if (n == 0) return 1;
    if (n == 1) return 1;
    if (n == 2) return 2;
    while (n > 2) {
        for (i = 0; i < n - 2; i++) {
            c = a + b;  
            a = b;
            b = c;
            n--;
        }
    }
    return c;
}