信息论基础 | 第七章 信道容量

2025-11-19 10:51:01 星期三
姨妈痛的要死...现在就是特别后悔选这个课，学数学的学这个，教材的符号看着超级难受

7.1 信道容量的例子

定义（信道容量）：离散无记忆信道的信息信道容量 (channel capacity) 定义为 \(C = \max_{p(x)} I(X; Y)\)，这里的最大值取自所有可能的输入分布 \(p(x)\)。

进一步：给出信道容量一个可操作的定义
定义（信道容量）：信道容量是信道的最高可达码率（单位：比特/信道使用），在此码率下，信息能够以任意小的差错概率传输。这即是香农第二定理的核心结论。

1. 离散信道 数学模型：\(\{X,p(y|x),Y\}\)
   如果输出概率仅依赖于输入符号，与以前的输入、输出均无关，这种信道称为无记忆信道(memoryless channel).

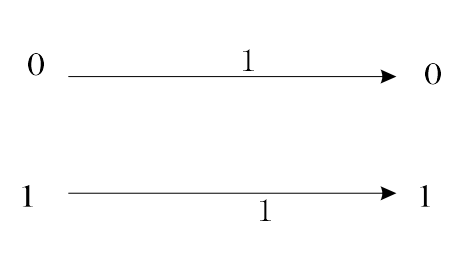
2. 无噪声二元信道
   传输比特无误接收，该信道一次可以传输1比特。可以简单通过信道容量的定义计算：在p(x)=(0.5, 0.5)时，有C=maxI(X;Y)=1 bit
   简单计算过程：设p(x=0)=p, p(x=1)=1-p , 下面计算\(I(X;Y)=H(Y)-H(Y|X)\), 因为是无噪声信道，所以传过去x就得到y，没有损失，所以\(H(Y)=H(X)\), \(H(Y|X)=0\), 对H(X)求max就有C=maxI(X;Y)=1 bit
   

3. 无重叠输出的有噪声信道
   

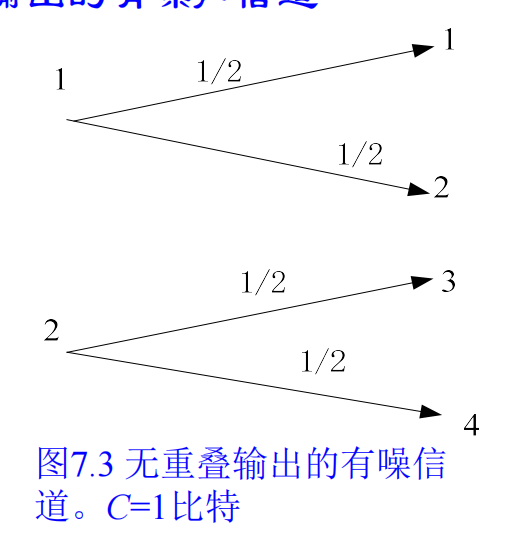
   尽管信道看起来有“噪声”（输入到输出的映射是随机的），但接收端能无错误地解码原始比特，因为输出集合被划分为两个不相交的子集 {1,2} 和 {3,4}，分别对应输入 0 和 1。
   下面我们来计算这个信道容量：\(I(X;Y)=H(Y)-H(Y|X)\), 假设\(p(X=0)=\omega,\quad p(X=1)=1-\omega\)

   • 计算\(H(Y|X)=H(Y|X=0)+H(Y|X=1)=\omega\cdot1+(1-\omega)\cdot1=1\)
   • 计算\(H(Y)\),Y的分布是\(\left(\frac{\omega}{2},\frac{\omega}{2},\frac{1-\omega}{2},\frac{1-\omega}{2}\right)\), 那么直接计算就有\(\begin{gathered} H(Y)=-2\cdot\frac{\omega}{2}\log\frac{\omega}{2}-2\cdot\frac{1-\omega}{2}\log\frac{1-\omega}{2} \\ =-\omega\log\frac{\omega}{2}-(1-\omega)\log\frac{1-\omega}{2} \\ =-\omega(\log\omega-1)-(1-\omega)(\log(1-\omega)-1) \\ =-\omega\log\omega-(1-\omega)\log(1-\omega)+\omega+(1-\omega) \\ =-\omega\log\omega-(1-\omega)\log(1-\omega)+1 \end{gathered}\)

   所以\(I(X;Y)=H(Y)-H(Y|X)=-\omega\log\omega-(1-\omega)\log(1-\omega)+1-1=-\omega\log\omega-(1-\omega)\log(1-\omega)\)， 在\(\omega=0.5\)时取最大值 1 比特。

4. 二元对称信道
   

\[\begin{aligned} I(X ; Y) & = H(Y) - H(Y \mid X) \\ & = H(Y) - \sum p(x) H(Y \mid X = x) \\ & = H(Y) - \sum p(x) H(p) \\ & = H(Y) - H(p) \\ & \leqslant 1 - H(p) \end{aligned} \]

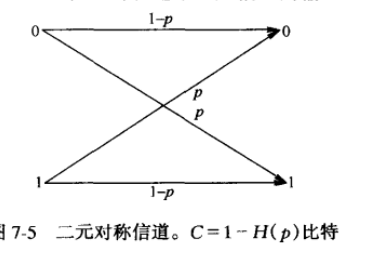
最后一个不等号是因为Y为二元随机变量。

4. 离散无记忆信道
   \(p(y^n| x^n)=\prod_{i=1}^{n} p(y_i|x_i)\)

5. 字母信道
   C=\log 13
   \begin{pmatrix}
   1/2& 1/2 & & & \
   0& 1/2 & 1/2 & & \
   & & 1/2& & \
   & & & & \
   1/2& & & &1/2
   \end

6. 二元删除信道
   二元删除信道(Binary Erasure Channel, BEC)。该二元信道的输入字符以概率α被删除。在接收端收到e，不能确定发送端比特。可以通过简单的计算，得出参数为α的二元删除信道的信道容量为C=1- α比特。计算过程如下：
   信道容量公式推导
   互信息定义为：

\[I(X;Y) = H(X) - H(X|Y) \]

• 输入 \(X\) 的最大熵 \(H(X)\) 在等概分布时达到，即 \(H(X) = 1\) 比特。

• 条件熵 \(H(X|Y)\) 的计算：
  - 若 \(Y=0\)：可确定 \(X=0\)，故 \(H(X|Y=0) = 0\)
  - 若 \(Y=1\)：可确定 \(X=1\)，故 \(H(X|Y=1) = 0\)
  - 若 \(Y=e\)：完全不知道 \(X\) 是 0 还是 1，故 \(H(X|Y=e) = H(X)\)

  出现 \(Y=e\) 的概率为 \(\alpha\)，因此：

  \[H(X|Y) = \alpha \cdot H(X) \]
  \[I(X;Y) = H(X) - \alpha H(X) = (1-\alpha) H(X) \]

  取max\(I(X;Y)\) ，取 \(H(X) = 1\)，得到信道容量：
  $$
  C = 1 - \alpha
  $$

练习：差错概率计算，二元对称信道(Binary Symmetric Channel, BSC)。该二元信道的输入字符以概率p=0.1互补。设X为等概二元信源，采用(3,1)重复码编码。计算平均误差概率\(P_{e}^{(3)}\)

sol. (3,1)重复码的意思是：把信息0编为000，信息1为111. **按多数表决译码 **， 比如0 的位数比1多，就译为0（比如001就代表信息0，110就代表1）。错误概率p=0.1。 信息源0 或1是等概率出现的。
下面计算：当信息为0的时候，收到的编码错两位或三位，那么译码结果就为1了，信息就错了，这个概率是\(p^'=C_3^2 0.1*0.1*0.9+0.1^3=0.028\), 而信息源等概率，那么平均误差概率就是20.5p^'=0.028

7.2 对称信道

定义 如果信道转移矩阵 \(p(y|x)\)的任何两行互相置换；任何两列也互相置换，那么称该信道是对称的(syrmmetric)。如果转移矩阵的每一行 \(p(\cdot|x)\)都是其他每行的置换，而所有列的元素和\(\sum_{x}p(y\mid x)\)相等，则称这个信道是弱对称的(weakly symmetric)。

定理7.2.1 对于弱对称信道，\(C=\log|\mathcal{Y}|-H(\)转移矩阵的行). 当输入字母表上的分布为均匀时达到该容量。

7.3 信道容量的性质

1. 由于\(I(X;Y)\geqslant0\),所以\(C\geqslant0\)。
2. 由于 \(C=\max I(X;Y)\leqslant\max H(X)\leqslant\log|\mathcal{X}|\),所以 \(C\leqslant\log|\mathcal{X}|\)。
3. \(C\leqslant \log | \mathcal{Y} |\),理由同上。
4. \(I( X; Y)\)是关于\(p(x)\)的一个连续函数。
5. \(I(X;Y)\)是关于 \(p(x)\)的凹函数(定理 2.7.4)。由于 \(I(X;Y)\)是闭凸集上的凹函数，因而局部最大值也是全局最大值。由上述性质 2 和 3 可以看出，最大值是有限的，这证实了在容量的定义中使用 max 而不用 sup 记号是合理的。

7.4 信道编码定理预览

Aim ：为什么我们能在有噪声的信道上，几乎无错误地传输信息，而且最高速率就是信道容量C？

采用分组编码：将信息打包成长序列( 长度为\(n\) ）发送。由于信道是离散无记忆的，序列的转移概率是每个符号独立转移概率的乘积。

• 固定发送一个典型输入序列 \(\mathbf{x}^n\)

• 由于噪声，接收端可能得到的输出序列 \(\mathbf{y}^n\)约有 \(2^{nH(Y|X)}\) 个典型结果，且它们等概出现。

• 不考虑发送什么，接收端所有可能出现的典型序列 \(\mathbf{y}^n\) 总数约为 \(2^{nH(Y)}\)

• 目标：使不同码字（不同 \(\mathbf{x}^n\)）对应的输出序列集合互不相交。

• 这样，收到任何 \(\mathbf{y}^n\) 都能唯一确定其对应的发送码字。

• 最大可区分的码字数量上限为：

  \[\frac{\text{总输出序列数}}{\text{每个输入对应的输出序列数}} = \frac{2^{nH(Y)}}{2^{nH(Y|X)}} = 2^{n[H(Y)-H(Y|X)]} = 2^{nI(X;Y)} \]

  那么，

  • 最大可区分码字数 \(M \leq 2^{nI(X;Y)}\)
  • 可传输信息比特数 \(k = \log_2 M\)
  • 码率 \(R = k/n \leq I(X;Y)\)
  • 对所有输入分布取最大值，即得信道容量 \(C = \max I(X;Y)\)
  • 因此，可靠传输的码率上限为 \(C\)

---

7.5 定义

1. 通信流程

• 消息 (Message): 需要传输的信息，记为 \(W\)，从有限集合 \(\{1, 2, \cdots, M\}\) 中均匀选取。
• 编码函数 (Encoding Function): 映射 \(X^{n}: \{1,2, \cdots, M\} \rightarrow \mathcal{X}^{n}\)，将每个消息 \(i\) 映射为码字 \(x^{n}(i)\)。
• 信道 (Channel): 由三元组 \((\mathcal{X}, p(y | x), \mathcal{Y})\) 表示，描述信号传输的统计特性。
• 译码函数 (Decoding Function): 确定性规则 \(g: \mathcal{Y}^{n} \rightarrow \{1,2, \cdots, M\}\)，为接收序列指定猜测消息 \(\hat{W}\)。

2. 离散无记忆信道 (DMC)

• 定义: 信道的 \(n\) 次扩展 \((\mathcal{X}^{n}, p(y^{n} | x^{n}), \mathcal{Y}^{n})\) 满足：
  \[p(y_k | x^{k}, y^{k-1}) = p(y_k | x_k), \quad k=1,2,\cdots,n \]

• 无反馈情形: 当输入不依赖过去输出时，转移概率简化为：
  \[p(y^{n} | x^{n}) = \prod_{i=1}^{n} p(y_i | x_i) \]

3. 误差概率

• 条件误差概率:
  \[\lambda_i = \Pr(g(Y^{n}) \neq i | X^{n} = x^{n}(i)) \]

• 最大误差概率:
  \[\lambda^{(n)} = \max_{i \in \{1,2,\cdots,M\}} \lambda_i \]

• 平均误差概率:
  \[P_e^{(n)} = \frac{1}{M} \sum_{i=1}^{M} \lambda_i \]
  当消息均匀分布时，\(P_e^{(n)} = \Pr(W \neq g(Y^{n}))\)。

4. 码率与容量

• 码率 (Rate):
  \[R = \frac{\log M}{n} \]

• 可达码率 (Achievable Rate): 存在 \(( \lceil 2^{nR} \rceil, n )\) 码序列，使得 \(n \rightarrow \infty\) 时 \(\lambda^{(n)} \rightarrow 0\)。
• 信道容量 (Channel Capacity): 所有可达码率的上确界，记为 \(C\)。

---

7.6 联合典型序列

先回顾以前的典型序列的定义：

设 \(X_1, X_2, \cdotp \cdotp \cdotp , X_n\) 是 概 率 密 度 函 数 为 \(p( x)\)的 i. i. d随机序列，满足下列条件：

\[\left|\frac{\log p(x_1,x_2,\cdots,x_n)}n+H(X)\right|<\varepsilon \]

或\(2^{-n(H(X)+\varepsilon)}\leq p(x_1,x_2,\cdots,x_n)\leq2^{-n(H(X)-\varepsilon)}\)

则称该源字母序列为典型序列，记为\(A_\mathrm{\varepsilon}^{(n)}\)

定义 服从分布 \(p(x,y)\) 的联合典型序列 \(\{(x^n,y^n)\}\) 所构成的集合 \(A_\epsilon^{(n)}\) 是指其经验熵与真实熵 \(\epsilon\) 接近的 \(n\) 长序列构成的集合，即：

\[A_\epsilon^{(n)}=\{(x^n,y^n)\in\mathcal{X}^n\times\mathcal{Y}^n: \]

\[\left|-\frac{1}{n}\log p(x^n)-H(X)\right|<\epsilon\]

\[\left|-\frac{1}{n}\log p(y^n)-H(Y)\right|<\epsilon \]

\[\left|-\frac{1}{n}\log p(x^n,y^n)-H(X,Y)\right|<\epsilon\}\]

其中

\[p(x^n,y^n)=\prod_{i=1}^{n}p(x_i,y_i) \]

---

回顾：
本章我们考虑编码问题，对于\({X , p(y|x), Y}\)的\((M,n)\)码：

1. 消息{1,...,M},
2. 编码\(X^n : {1,...,M} \to X^n\)
3. 译码 \(g:y^n \to {1,...,M}\)
   为了评估编码的效果，我们定义
4. 条件误差概率 \(\lambda _i =P(g(y^n)\neq i |X^n(i))\)
5. 最大误差概率 $\lambda=\max \lambda _i $
6. 码率 \(R=(log M )/n\) bit

为了介绍香农编码定理，我们引入联合典型序列的概念：序列对 \((x^n, y^n)\) 是联合典型的，如果它满足：

1. \(|-\frac{1}{n} \log p(x^n) - H(X)| < \varepsilon\)
2. \(|-\frac{1}{n} \log p(y^n) - H(Y)| < \varepsilon\)
3. \(|-\frac{1}{n} \log p(x^n, y^n) - H(X, Y)| < \varepsilon\)

---

7.11 汉明码

1. 核心思想：冗余与纠错

核心问题：如何在不可靠信道中可靠传输信息。

基本方法：通过增加冗余，使接收方能检测和纠正错误。

简单例子：重复码（如1→11111），通过多次传输同一信息提高可靠性，但代价是码率低（1/5比特/字符）。

2. 奇偶校验码

现在信息发出方和接收方约定一种特殊的编码，我们在编码的最后加上一位“奇偶校验码”，用来判断接收方收到的码字是否有错。我们举例说明：

• 接收方收到码字101010，校验码是最后一位1，校验码定义是（在模2加法下)将前面的数字加起来1+0+1+0+1=1，但这个结果不等于校验码1，说明这个码字出错了。

3. 奇偶校验码的推广：汉明码

在2中我们介绍了奇偶校验码的思想，但只有一位奇偶校验码是不够的，无法检测偶数次错误。下面我们就推广奇偶校验码，希望码字里面多一些位数作为校验码！

我们先举一个例子：

• 以下运算都是模2加法，我们在\(F_2\)上讨论
• 考虑所有长度为3的非0二元向量的集合（这样的向量一共有\(2^3-1\)个），我们将这些向量作为列向量排在一起，作为一个矩阵：

\[H = \left[\begin{array}{lllllll} 0 & 0 & 0 & 1 & 1 & 1 & 1 \\ 0 & 1 & 1 & 0 & 0 & 1 & 1 \\ 1 & 0 & 1 & 0 & 1 & 0 & 1 \end{array}\right] \]

• 现在考虑\(H\)的零空间：即所有满足\(H c^T = 0\)的向量\(c\)的集合。写成方程组的形式：

\[\begin{cases} 0\cdot c_1 + 0\cdot c_2 + 0\cdot c_3 + 1\cdot c_4 + 1\cdot c_5 + 1\cdot c_6 + 1\cdot c_7 = 0 \quad (\text{mod } 2) \\ 0\cdot c_1 + 1\cdot c_2 + 1\cdot c_3 + 0\cdot c_4 + 0\cdot c_5 + 1\cdot c_6 + 1\cdot c_7 = 0 \quad (\text{mod } 2) \\ 1\cdot c_1 + 0\cdot c_2 + 1\cdot c_3 + 0\cdot c_4 + 1\cdot c_5 + 0\cdot c_6 + 1\cdot c_7 = 0 \quad (\text{mod } 2) \end{cases} \]

• 由于\(H\)的秩为3，那么零空间的维数为4，用线性方程组的理论，也就是说，只有四个变量是自由的，其他三个变量被约束了，这三个变量就是校验码！
• \(Hx=0\)解空间的维数为4，那么有\(2^4\)个向量满足该方程，这些是合法码字，剩余的\(2^7-2^4\)个码字都不能满足\(Hx=0\)，是非法码字（即有错误）

下面我们总结汉明码的性质

1. 线性性 任意两个码字相加还是码字
2. 最小重量与最小距离
   • 最小重量：除全零码字外，码字中“1”的最小个数（本例中为3）
   • 最小距离：任意两个不同码字之间不同的最小位数（本例中为3）
   • 关系：对于线性码而言，两者相等（我们以定理的形式给出证明）

定理：对于任意线性码 \(C\)，有 \(d_{\min}(C) = w_{\min}(C)\)。

证明：设 \(C\) 是一个定义在二元域 \(F_2\) 上的线性码。\(d_{\min}(C)\) 表示 \(C\) 的最小距离，\(w_{\min}(C)\) 表示 \(C\) 的最小重量。
对于 \(C\) 中任意两个不同的码字 \(c_1, c_2 \in C\)，由于 \(C\) 是线性子空间，它们的差 \(c_1 - c_2\)（在模2运算下等价于 \(c_1 + c_2\)）仍然属于 \(C\)。两个码字之间的汉明距离定义为它们在不同位置上的个数，这正好等于它们的差的汉明重量，即：

\[d(c_1, c_2) = w(c_1 - c_2) \]

设 \(c_0\) 是 \(C\) 中一个重量最小的非零码字，即 \(w(c_0) = w_{\min}(C)\)。考虑 \(c_0\) 与零码字 \(0\)（零码字总是属于线性码 \(C\)）这一对码字：

\[d(c_0, 0) = w(c_0 - 0) = w(c_0) = w_{\min}(C) \]

因为 \(d_{\min}(C)\) 是所有不同码字对距离的最小值，而 \(d(c_0, 0)\) 是其中一个具体的距离值，所以有：

\[d_{\min}(C) \leq w_{\min}(C) \]

设 \(c_1, c_2 \in C\) 是一对使得距离达到最小值的码字，即 \(d(c_1, c_2) = d_{\min}(C)\)。令 \(c = c_1 - c_2\)，则 \(c \in C\) 且 \(c \neq 0\)（因为 \(c_1 \neq c_2\)）。根据距离与重量的关系：

\[w(c) = w(c_1 - c_2) = d(c_1, c_2) = d_{\min}(C) \]

因为 \(w_{\min}(C)\) 是所有非零码字重量的最小值，而 \(w(c)\) 是其中一个具体的重量值，所以有：

\[w_{\min}(C) \leq d_{\min}(C) \]

这就完成了证明。

4. 汉明码纠错分析

1. 例子
   考虑(7,4)汉明码，最小距离 \(d_{\min} = 3\)。
   假设两个码字：

   • \(c_1 = 0100101\)（原始发送码字）
   • \(c_2 = 1000011\)（另一个码字）
     这两个码字之间的距离为3（在3个位置上不同）。

2. 出错情况
   发送 \(c_1 = 0\ 1\ 0\ 0\ 1\ 0\ 1\)
   假设第3位出错：\(0 \rightarrow 1\)
   接收序列：\(r = 0\ 1\ \mathbf{1}\ 0\ 1\ 0\ 1\)

3. 距离比较

   • \(r\) 与 \(c_1\) 的距离：只有第3位不同 → \(d(r, c_1) = 1\)
   • \(r\) 与 \(c_2\) 的距离：比较所有位，发现第1,2,3,5,6位不同 → \(d(r, c_2) = 5\)

4. 一般情况的证明
   设原始码字为 \(c\)，另一个任意码字为 \(c'\) (\(c' \neq c\))，接收序列 \(r\) 由 \(c\) 仅错1位得到：

   • \(d(r, c) = 1\)
   • 由三角不等式：\(d(c, c') \leq d(c, r) + d(r, c')\)
   • 代入：\(3 \leq 1 + d(r, c')\)，得 \(d(r, c') \geq 2\)

   结论：\(r\) 与原始码字 \(c\) 的距离为1，与其他任何码字的距离至少为2。因此 \(c\) 是距离 \(r\) 最近的码字，可以唯一确定地纠错。

5. 练习
   依然考虑本节的矩阵H，设接收端收到
   \(\boldsymbol{r}_1=(1000011)\)
   \(\boldsymbol{r}_2=(0000011)\)
   \(\boldsymbol{r}_3=(0100011)\)
   求相应的译码码字。
   Sol. 计算Hr_i是否为0，

• 对于\(r_1\)满足，说明正确，译码码字就是\(\boldsymbol{r}_1=(1000011)\)。
• 对于\(r_2\)，计算结果为\((0,0,1)^T\), 我们去找\((0,0,1)^T\)在H的位置，是第1列，说明码字错误发生在第一位，我们为了得到正确的码字，需要将第一位翻转，于是正确的码字是1000011, 我们将新的码字带入\(Hx\)进行计算，得到的结果为0，说明该码字确实只错了一位。
• 对于\(r_3\), 计算结果为\((0,1,1)^T\)，对应H的第2列，翻转第二位bit，得到0000011，但这个码字只有2个1（去看最小重量那里的知识点），不可能是合法码字

---

回顾：
汉明码（7，4）

• 校验矩阵H: 将\(2^{7-4}-1\)个非零向量排列为\((P|I_3)_{3*7}\)的形式
• 生成矩阵G: \(G=(I_4|P^T)_{4*7}\)
• 编码：输入\(u=(u1,...,u_4)\), 输出\(c=uG=(u|uP^T)\)
  概念与性质
• 线性码：由1-3构成的码
• 零空间：码空间是H的零空间，由于\(r(H)=3\), 所以零空间的维数为4
• 重量： \(w(c)\)表示向量c中非零分量的个数，本例子中最小重量为3
• 距离：\(d(x,y)\)为两个向量不同分量的个数
• 在线性码中，\(d(x,y)=w(x+y)\)
• 性质：该编码可以纠正一位错误.

---

6. 系统码

7. Venn图解释汉明码工作原理

8. 汉明码的推广

7.12 反馈容量

反馈容量\(C_{FB}\)为反馈信道可达的上确界
性质： \(C_{FB}=C\)
信源信道编码定理：\(H<C\)是\(P_e \to 0\)的充要条件