【字符串】总结 6:AC 自动机
问题:给定 \(n\) 个模式串和 \(1\) 个文本串,求解有多少个模式串在文本串中出现过。
朴素的想法是做 \(n\) 次 KMP,但时间复杂度太高,难以接受,这时就要用到 AC 自动机了。
AC 自动机的基本思想
假设现在的文本串为 \(s=\text{abcdbc}\),模式串为 \(t_1=\text{abc},t_2=\text{bd},t_3=\text{bcd},t_4=\text{c}\),我们对所有的模式串 \(t_i\) 建立一棵 Trie:
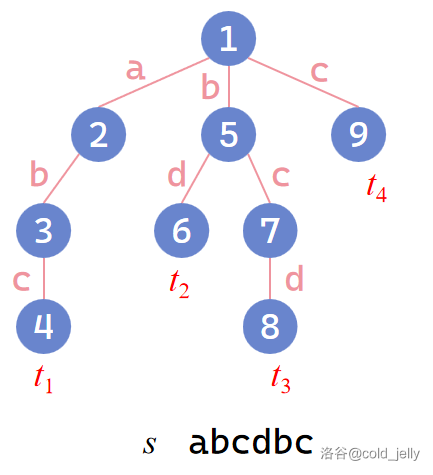
我们用文本串 \(s\) 在 Trie 上匹配,先在 \(1\to 2\to 3\to 4\) 路径上匹配,成功匹配到 \(t_1\),然后就不能继续匹配了(如下图),此时难道要从根节点重新开始匹配吗?
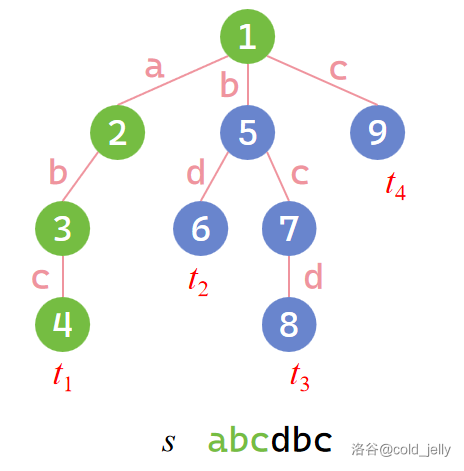
我们发现此时在 Trie 上,我们珂以跳到 \(7\) 号点上继续匹配,然后匹配到 \(8\) 号点:
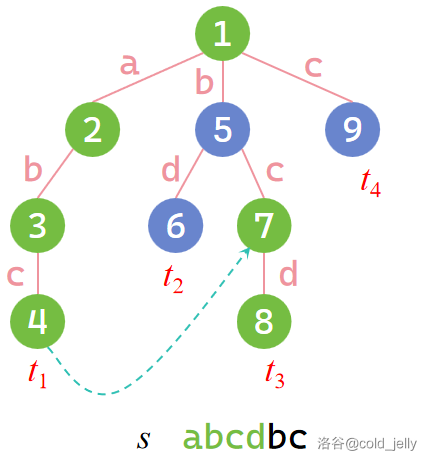
也就是说,AC 自动机的基本思想就是用类似 KMP 算法的思想达到“聪明”地“跳”的目的。
问题来了,我们该如何确定我们要“跳”到哪个点呢?类似与 KMP 算法的 \(nxt\) 数组,我们采用 fail 指针,即若在 \(i\) 号点匹配失败后跳到 \(j\) 号点匹配,称 \(j\) 是 \(i\) 的 fail 指针,我们把它记作 \(fail(i)=j\)。
fail 指针的意义是:如果 \(fail(i)=j\),那么在 Trie 上,根节点到 \(j\) 对应的字符串是根节点到 \(i\) 对应的字符串的后缀,并且这个后缀是 Trie 上所有满足条件的后缀中最长的(也就是深度最大的 \(j\)),例如就上面的例子而言,路径 \(1\to i(i=4)\) 对应的字符串为 \(\text{abc}\),其在 Trie 上的后缀有 \(1\to 7\) 对应的 \(\text{bc}\) 和 \(1\to 9\) 对应的 \(\text{c}\),但前者的长度更大,因此 \(fail(4)=7\)。
fail 指针的求法
首先,因为后缀指针对应路径的字符串是后缀,所以 \(fail(i)\) 的深度一定小于 \(i\)。故与根节点的子节点的 fail 指针一定指向根节点。
点 \(i\) 的父节点为 \(fa[i]\),如果 \(fail(fa[i])\) 有与到 \(i\) 字符指针一样的节点 \(j\),那么必定有 \(fail(i)=j\)。具体可结合下面的图示理解。在下图中,我们要求 \(fail(i)\),我们观察知道其对应的字符串为 \(\text{xabc}\) 的最长后缀是 \(\text{abc}\)。而 \(fa[i]\) 对应的字符串为 \(\text{xab}\),又已知 \(fail(fa[i])\) 对应的最长后缀为 \(\text{ab}\),并且 \(fail(fa[i])\) 到其中一个子节点的字符指针为 \(\text{c}\),恰与 \(fa[i]\) 到 \(i\) 的字符指针相同,故该子节点对应的字符串 \(\text{abc}\) 一定是我们要求的最长后缀。(可能有点绕哈,多看几遍图就行了)
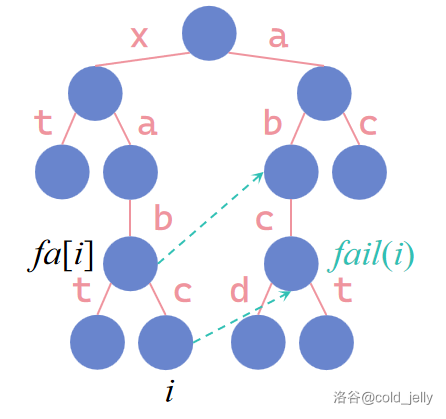
因此我们珂以采用 BFS 来求 fail 指针。
const int N = _______;
int tr[N][26];//Trie,默认 Σ 为小写字母集
int fail[N];
void getfail()
{
queue<int> q;
for(int i = 0; i < 26; i ++) tr[0][i] = 1;
fail[1] = 0;
// 建立一个虚拟的 0 号节点
// 将 0 的所有子节点全部指向 1(根节点)
// 再将 1 指向 0 号节点
// 这样效果等价于上述第一种情况
q.push(1);//根压入队列
while(q.size())//广搜
{
int u = q.front();
q.pop();
for(int i = 0; i < 26; i ++)
{
int v = tr[u][i];
// fail[u] 即为 fail(fa[u])
// tr[fail[u]][i] 和 v 字符指针相同
if(!v)
{
tr[u][i] = tr[fail[u]][i];
continue;
}
fail[v] = tr[fail[u]][i];
q.push(v);
}
}
}
问题求解
求出了 fail 指针,我们便珂以在原先 Trie 的基础上添加跳 fail 的操作了。
为了避免重复计算,我们每经过一个点就打个标记,下一次经过就不重复计算了。
const int N = _______;
int tr[N][2];
int fail[N], st[N];
int search(char* s)
{
int res = 0;
int len = strlen(s), p = 1;
for(int i = 0; i < len; i ++)
{
int c = s[i] - 'a';
int k = tr[p][c];
while(k > 1 && st[k] != -1)
{
ans += st[k];//累计模式串个数
st[k] = -1;//打标记
k = fail[k];//跳 fail
}
p = tr[p][c];
}
}
再回看问题:
问题:给定 \(n\) 个模式串和 \(1\) 个文本串,求解有多少个模式串在文本串中出现过。
我们利用 AC 自动机,可以写出代码了:
#include<bits/stdc++.h>
using namespace std;
const int N = 1e6 + 10;
int n, ans = 0;
struct AC
{
int cnt = 1;//编号从 1 开始
int tr[N][26];
int fail[N], st[N];
void getfail()
{
queue<int> q;
for(int i = 0; i < 26; i ++) tr[0][i] = 1;
fail[1] = 0;
// 建立一个虚拟的 0 号节点
// 将 0 的所有子节点全部指向 1(根节点)
// 再将 1 指向 0 号节点
// 这样效果等价于上述第一种情况
q.push(1);//根压入队列
while(q.size())//广搜
{
int u = q.front();
q.pop();
for(int i = 0; i < 26; i ++)
{
int v = tr[u][i];
// fail[u] 即为 fail(fa[u])
// tr[fail[u]][i] 和 v 字符指针相同
if(!v)
{
tr[u][i] = tr[fail[u]][i];
continue;
}
fail[v] = tr[fail[u]][i];
q.push(v);
}
}
}
void insert(char* s)
{
int len = strlen(s), p = 1;
for(int i = 0; i < len; i ++)
{
int c = s[i] - 'a';
if(tr[p][c] == 0) tr[p][c] = ++ cnt;
p = tr[p][c];
}
st[p] ++;
}
void search(char* s)
{
int len = strlen(s), p = 1;
for(int i = 0; i < len; i ++)
{
int c = s[i] - 'a';
int k = tr[p][c];
while(k > 1 && st[k] != -1)
{
ans += st[k];//累计模式串个数
st[k] = -1;//打标记
k = fail[k];//跳 fail
}
p = tr[p][c];
}
}
}T;
char s[N];
int main()
{
cin >> n;
for(int i = 1; i <= n; i ++)
{
scanf("%s", s);//模式串
T.insert(s);
}
T.getfail();
scanf("%s", s);//文本串
T.search(s);
cout << ans;
return 0;
}
模板题
- P3808 AC 自动机(简单版)(就是上面的例题);
- P3796 AC 自动机(简单版 II)(求在文本串中出现最多次的模式串);
- P5357 【模板】AC 自动机。
这里给出 P3796 的代码实现,大致与例题一样:
#include<bits/stdc++.h>
using namespace std;
const int N = 1e6 + 10;
int n, ans = 0;
int num[N];
struct AC
{
int cnt = 1;//编号从 1 开始
int tr[N][26];
int fail[N], st[N];
void init()
{
cnt = 1, ans = 0;
memset(tr, 0, sizeof tr);
memset(fail, 0, sizeof fail);
memset(st, 0, sizeof st);
memset(num, 0, sizeof num);
}
void getfail()
{
queue<int> q;
for(int i = 0; i < 26; i ++) tr[0][i] = 1;
fail[1] = 0;
// 建立一个虚拟的 0 号节点
// 将 0 的所有子节点全部指向 1(根节点)
// 再将 1 指向 0 号节点
// 这样效果等价于上述第一种情况
q.push(1);//根压入队列
while(q.size())//广搜
{
int u = q.front();
q.pop();
for(int i = 0; i < 26; i ++)
{
int v = tr[u][i];
// fail[u] 即为 fail(fa[u])
// tr[fail[u]][i] 和 v 字符指针相同
if(!v)
{
tr[u][i] = tr[fail[u]][i];
continue;
}
fail[v] = tr[fail[u]][i];
q.push(v);
}
}
}
void insert(char* s, int m)
{
int len = strlen(s), p = 1;
for(int i = 0; i < len; i ++)
{
int c = s[i] - 'a';
if(tr[p][c] == 0) tr[p][c] = ++ cnt;
p = tr[p][c];
}
st[p] = m;
}
void search(char* s)
{
int len = strlen(s), p = 1;
for(int i = 0; i < len; i ++)
{
int c = s[i] - 'a';
int k = tr[p][c];
while(k > 1)
{
if(st[k]) num[st[k]] ++;
k = fail[k];
}
p = tr[p][c];
}
}
}T;
char s[151][N], t[N];
int main()
{
while(1)
{
scanf("%d", &n);
if(!n) break;
T.init();
for(int i = 1; i <= n; i ++)
{
scanf("%s", s[i]);//模式串
T.insert(s[i], i);
}
T.getfail();
scanf("%s", t);//文本串
T.search(t);
for(int i = 1; i <= n; i ++) ans = max(num[i], ans);
printf("%d\n", ans);
for(int i = 1; i <= n; i ++)
if(num[i] == ans) printf("%s\n", s[i]);
}
return 0;
}


 浙公网安备 33010602011771号
浙公网安备 33010602011771号