【字符串】总结 3：字典树（Trie）基础

顾名思义，字典树就是一棵功能很像字典的一棵树。

我们在查单词时，往往是先按照首字母，再按照第二个字母，以此类推地查询我们想要的单词的。字典树通过将树的边赋为一个个字符，从而使我们能够一层层像查单词一样得到字符串的。

Trie 的基本结构

先放图哈：

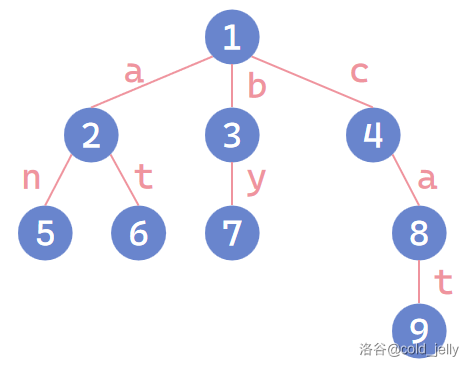
在上图所示的 Trie 中，通过对于从根节点到叶子节点的一条路径，我们可以得到 \(\text{an},\text{at},\text{by},\text{cat}\) 四个字符串。

因此，Trie 的每个节点都拥有若干字符指针，通过字符指针的不断指向，直到叶子节点，我们可以得到 Trie 中存储的字符串。

Trie 的插入操作

Trie 的插入操作（insert），即将一个字符串 \(s\) 插入 Trie 中。此时我们令一个指针 \(p\) 指向根节点，然后依次扫描 \(s\) 中的每个字符 \(c\)，分类讨论：

• 若 \(p\) 的 \(c\) 字符指针已指向节点 \(q\)，则令 \(p=q\)；
• 否则即指向空，则新建节点 \(q\)，并令 \(p\) 的 \(c\) 字符指针指向 \(q\)，然后令 \(p=q\)。

扫描完毕后，在当前节点上标记其是该插入字符串的末尾。

代码实现时，我们通常使用二维数组 \(tr\) 存储 Trie 的信息，其中 \(tr(i,x)\) 代表节点 \(i\) 的 \(x\) 字符指针指向的节点编号，其中 \(x\in\Sigma\)。也就是说，Trie 的空间复杂度为 \(O(n|\Sigma|)\)，\(n\) 为节点个数。

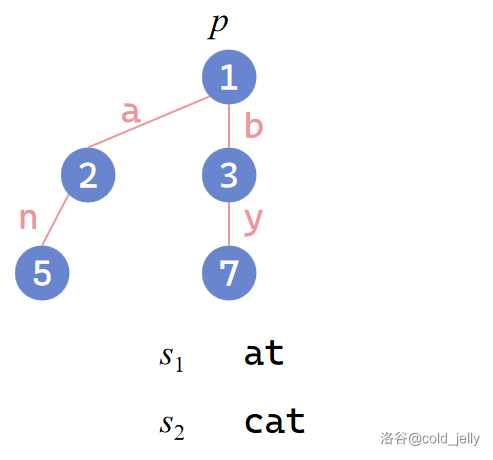
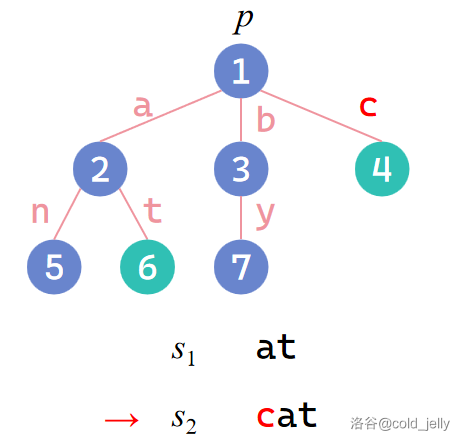
具体可通过图示理解（要在 Trie 中插入 \(s_1=\text{at}\) 和 \(s_2=\text{cat}\)）：

插入 \(s_1\)：

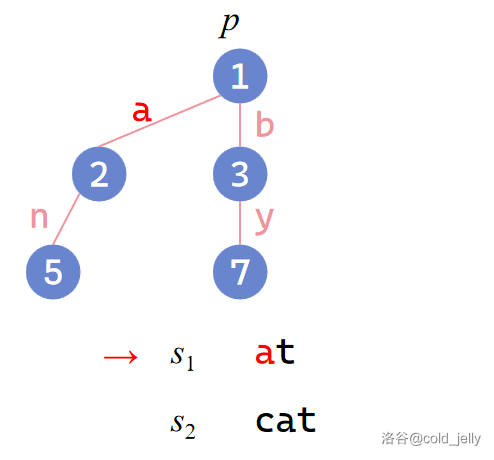
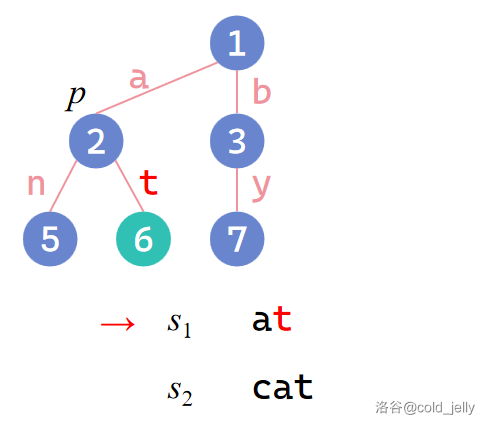
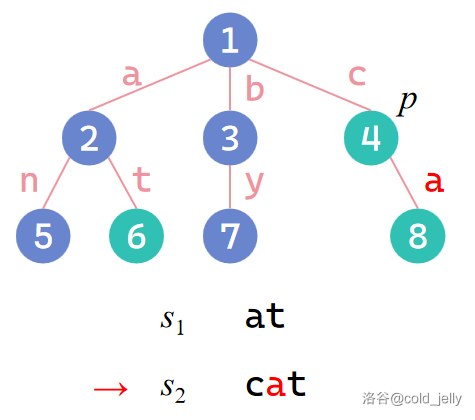
插入 \(s_2\)：

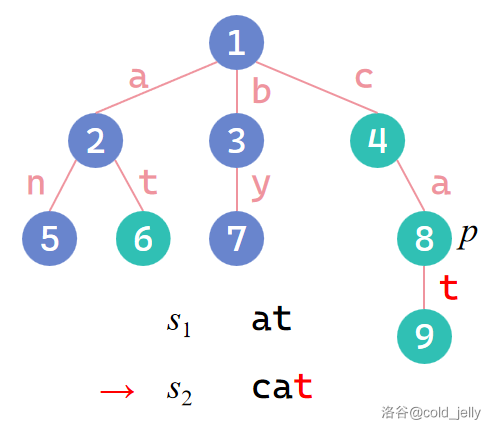
Trie 的查询操作

Trie 的查询操作（search），即在 Trie 中查询是否存储有字符串 \(s\)。其操作方法与插入类似。我们令一个指针 \(p\) 指向根节点，然后依次扫描 \(s\) 中的每个字符 \(c\)，分类讨论：

• 若 \(p\) 的 \(c\) 字符指针指向空，则说明 \(s\) 不在 Trie 中；
• 否则其指向节点 \(q\)，令 \(p=q\)。

若扫描完毕，若 \(p\) 被标记为某个字符串的末尾，则证明 \(s\) 在 Trie 中。

Trie 的代码实现

这里是结构体封装的 Trie 实现：

struct Trie
{
	int tr[N][26], cnt;
	bool st[N];
	void insert(char* s)
	{
		int len = strlen(s), p = 1;
		for(int i = 0; i < len; i ++)
		{
			int c = s[i] - 'a';
			if(tr[p][c] == 0) tr[p][c] = ++ cnt;
			p = tr[p][c];
		}
		st[p] = true;
	}
	bool search(char* s)
	{
		int len = strlen(s), p = 1;
		for(int i = 0; i < len; i ++)
		{
			int c = s[i] - 'a';
			p = tr[p][c];
			if(p == 0) return false;
		}
		return st[p];
	}
}T;