【字符串】总结 2：KMP 算法

字符串匹配

字符串匹配问题可以总结为下面这个问题：

给定字符串 \(s\) 和 \(t\)，在 \(s\) 中寻找 \(t\)（这个子串）。

KMP 算法可以在 \(O(|s|+|t|)\) 的复杂度内求解该问题。

BF 算法

在 KMP 算法前，先看看暴力做法（BF 算法）。

不妨令问题中的 \(s=\text{AAABAAAC},t=\text{AAAC}\)。

BF 算法的思路就是，每次以 \(s[i]\) 为起点开始与 \(t[j]\) 匹配，如果 \(s[i]=t[j]\)，则 \(j\) 加 \(1\)，继续匹配；如果 \(s[i]\ne t[j]\)，则 \(i\) 加 \(1\)，\(j\) 被置为 \(t\) 的起始下标。直到某次匹配发现所有字符均成功匹配时结束。

对于例子而言，可用下面的图示解释：

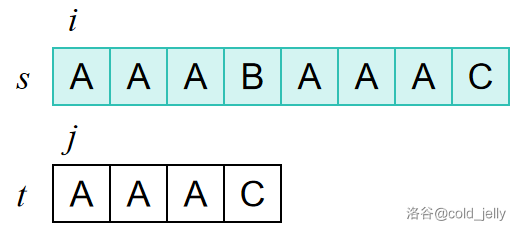
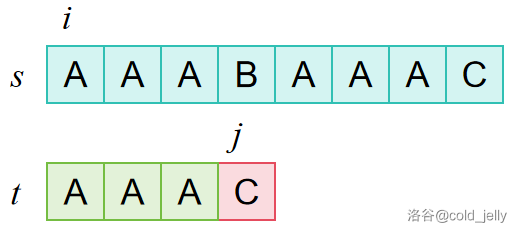
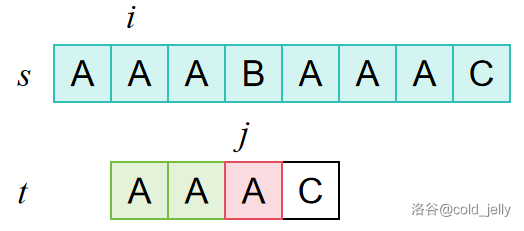
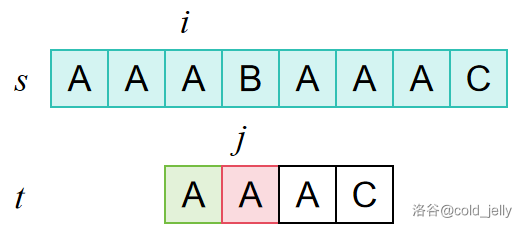
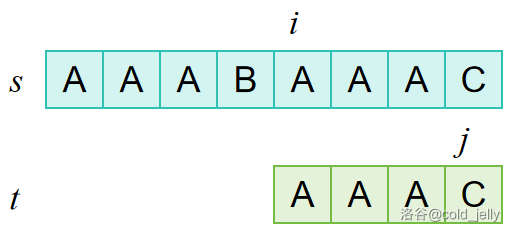
最坏情况下，BF 算法的时间复杂度为 \(O(|s||t|)\)。

我们发现，BF 算法中 \(j\) 在每次“失配”时都会跳回到初始状态，但很显然在例子中我们得知在 \(i=1,j=4\) 的这次匹配中前三个字符均匹配，那么之后在 \(i\in[2,4]\) 的匹配中一定会失配，因此这些匹配是多余的。

KMP 算法通过 \(nxt\) 数组，使 \(j\)“聪明”地回退，从而让时间复杂度降为线性。

\(nxt\) 数组的求法

\(nxt\) 数组的本质是寻找子串中相同前后缀的长度，并且一定是最长的前后缀，而且该前后缀不能为字符串本身。即一般地，对于字符串 \(s\)，\(nxt[i]=\max\{|pre(s[1\sim i])|\},pre(s[1\sim i])=suf(s[1\sim i])\)，且 \(nxt[i]\ne |s|\)，其中符号 \(pre(u)\) 与 \(suf(u)\) 分别代表 \(u\) 的前缀与后缀。

例如对于字符串 \(s=\text{ABABC}\)：

• \(nxt[1]\)：直接为 \(0\)；
• \(nxt[2]\)：没有相同的前后缀，故为 \(0\)；
• \(nxt[3]\)：拥有 \(\text{A}\) 这个相同的前后缀，故为 \(1\)；
• \(nxt[4]\)：拥有 \(\text{AB}\) 这个相同的前后缀，故为 \(2\)；
• \(nxt[5]\)：不存在相同的前后缀，故为 \(0\)。

如何求解 \(nxt\) 数组呢？我们可以先看看这样一个暴力做法。

例如对于字符串 \(u=\text{ABACABAB}\)，我们希望求其 \(nxt\) 数组：

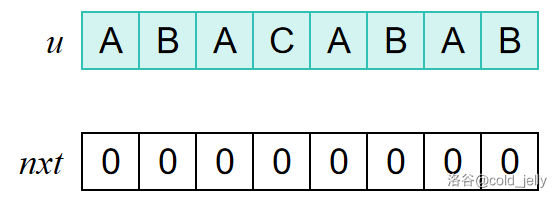
首先我们考虑递推求解 \(nxt\) 数组，即用已知的 \(nxt\) 值得出要求的 \(nxt\) 值。

不妨假设此时已得到 \(nxt[6]\) 的值：

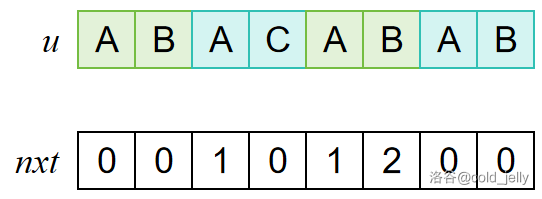
接下来又有下面一位的字符相同，因此构成了更长的相同前后缀，其长度为之前加 \(1\)，即有 \(nxt[7]=3\)：

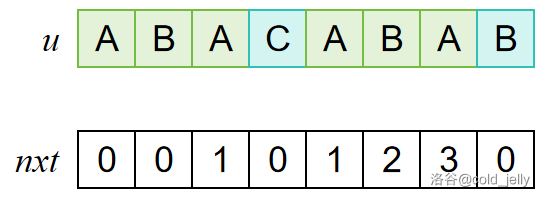
但是当到再下一位时，发现匹配失败了：

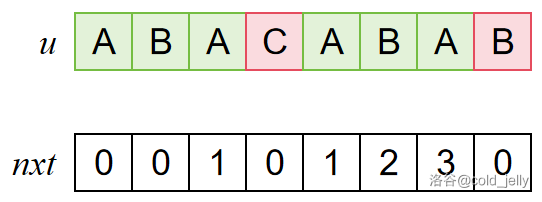
此时暴力做法发现 \(\text{ABAC}\ne \text{ABAB}\)，它将会尝试寻找更短的答案，下一步将缩短，比较出 \(\text{ABA}\ne \text{BAB}\)，继续缩短得到 \(\text{AB}=\text{AB}\)，则得到 \(nxt[8]=2\)。上述步骤可用下面的图示解释：

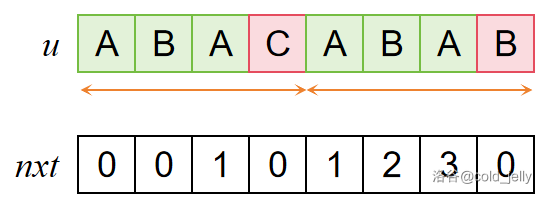
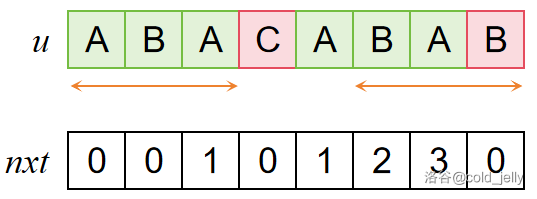
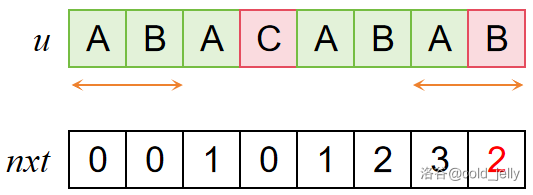
暴力做法明显不优。我们考虑到之前已经知道 \(u[1\sim 3]=u[5\sim 7]\)，且我们已知 \(nxt[3]=1\)，因此我们可以直接从 \(pre(u[1\sim 3])=suf(u[5\sim 7])\) 的位置开始重新比较：

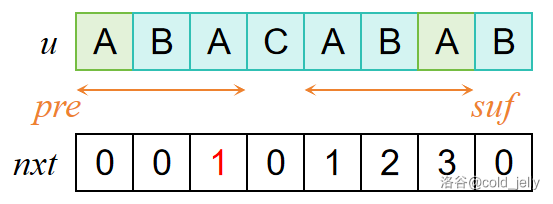
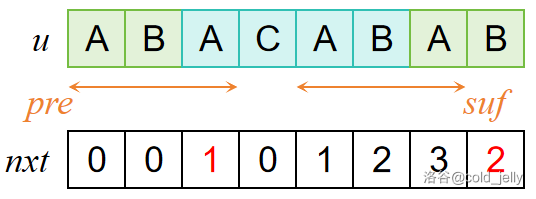
得到了 \(nxt[8]=2\)。这样的思路就是计算 \(nxt\) 数组的思路了：

const int N = _______;
int n;
char s[N];
int nxt[N];
void init()
{
	for(int i = 2, j = -1; i <= n; i ++)
	{
		while(j != -1 && s[i] != s[j + 1]) j = nxt[j];
		if(s[i] == s[j + 1]) j ++;
		nxt[i] = j;
	}
}

这样可以在线性复杂度内求得 \(nxt\) 数组。

KMP 算法

理解了 \(nxt\) 数组的求解方法，我们便可以通过 \(nxt\) 数组快速解决字符串匹配问题。

还是以 \(s=\text{AAABAAAC},t=\text{AAAC}\) 为例，此时我们可以求得 \(t\) 的 \(nxt\) 数组，如图所示：

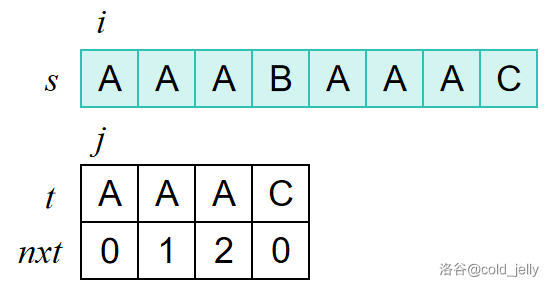
然后匹配：

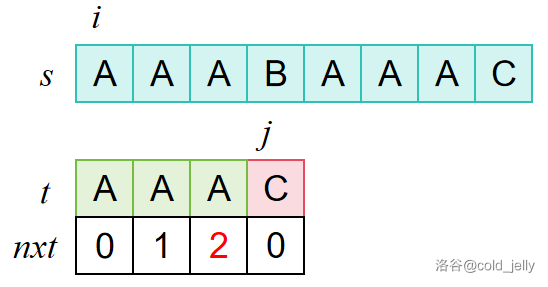
“失配”后，查找上一个位置的 \(nxt\) 值，发现值为 \(2\)，因此我们跳过两个字符：

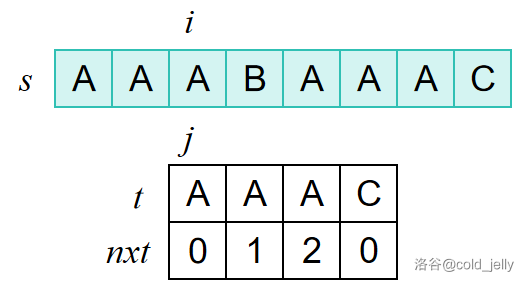
继续匹配：

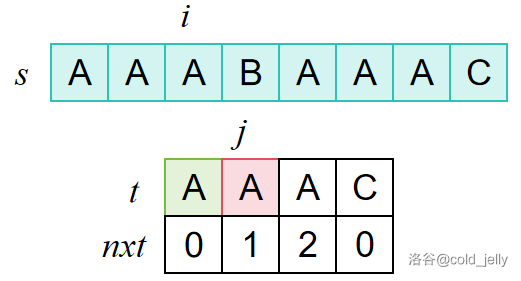
以此类推，直到匹配成功：

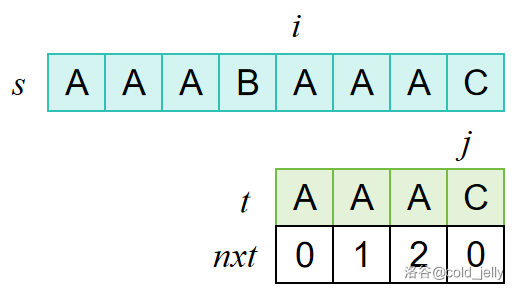
相应地，我们可以写出 KMP 算法的代码：

int kmp(char* s, char* t)
{
	int i = 0, j = 0;//这里下标从 0 开始 
	int n = strlen(s), m = strlen(t);
	while(i < n && j < m)
	{
		if(j == -1 || s[i] == t[j]) i ++, j ++;
		else j = nxt[j];
	}
	if(j == m) return i - j;//返回 t 在 s 中的位置 
	else return -1;//未匹配到 t 
}