大家好~本文推导全连接层的前向传播、后向传播、更新权重和偏移的数学公式，其中包括两种全连接层：作为输出层的全连接层、作为隐藏层的全连接层。
神经网络前向和后向传播推导（一）：前向传播和梯度下降
神经网络前向和后向传播推导（二）：全连接层
构建神经网络
我们构建一个三层神经网络，由一层输入层+两层全连接层组成：
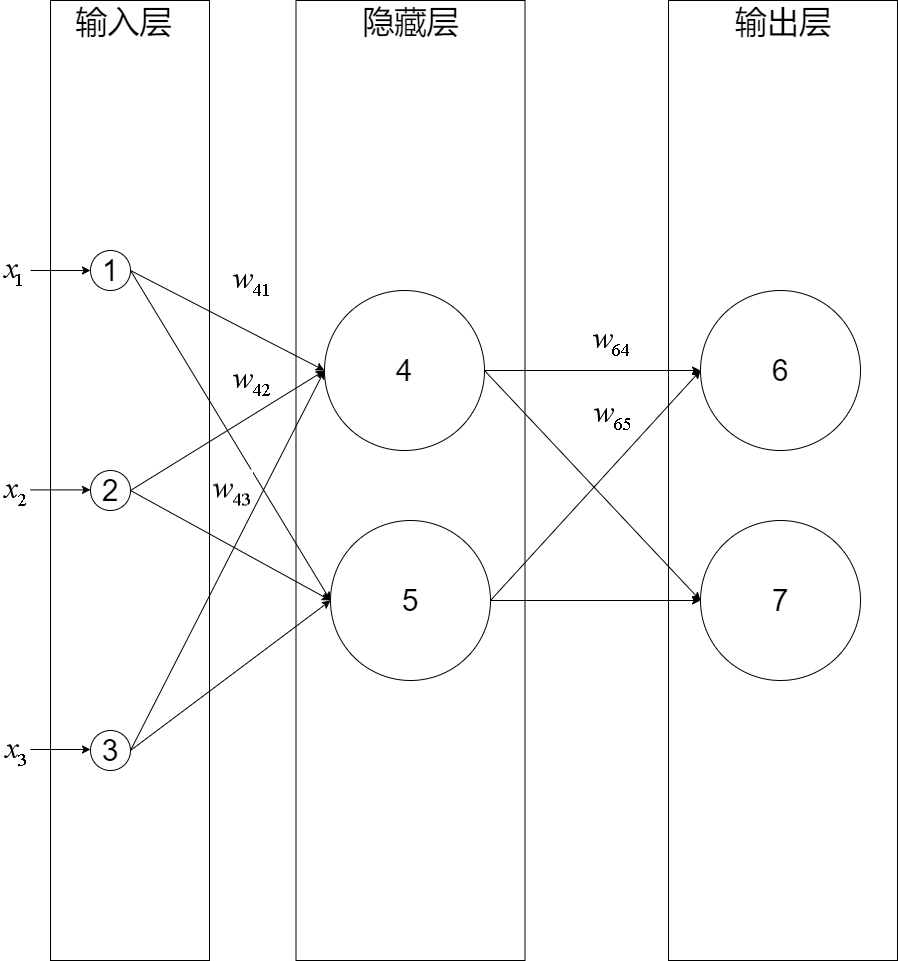
输入层有三个节点，我们将其依次编号为1、2、3；隐藏层的两个节点，编号依次为4、5；输出层的两个节点编号为6、7。因为我们这个神经网络是全连接网络，所以可以看到每个节点都和上一层的所有节点有连接。比如，我们可以看到隐藏层的节点4，它和输入层的三个节点1、2、3之间都有连接，其连接上的权重分别为\(w_{41}, w_{42}, w_{43}\)
（注意：权重的序号的命名规则是下一层的序号在上一层的序号之前，如为\(w_{41}\)而不是\(w_{14}\)）
推导前向传播
节点4的输出值\(y_4\)的计算公式为：
\[y_4=f(\vec{w_4}^T\cdot\vec{x})
\]
其中：
\[\vec{w_4} = [w_{41}, w_{42}, w_{43}, w_{b_4}]
\]
\[\vec{x} =
\begin{bmatrix}
x_1\\
x_2\\
x_3\\
1 \\
\end{bmatrix}
\]
\[f为激活函数
\]
推导隐藏层的前向传播
我们把隐藏层的权重向量组合在一起成为矩阵，就推导出隐藏层的前向传播计算公式了：
\[\overrightarrow{y_{隐藏层}}=f(W_{隐藏层}\cdot\vec{x})
\]
其中：
\[W_{隐藏层} = \begin{bmatrix}
\vec{w_4} \\
\vec{w_5} \\
\end{bmatrix} =\begin{bmatrix}
w_{41}, w_{42}, w_{43}, w_{b_4} \\
w_{51}, w_{52}, w_{53}, w_{b_5} \\
\end{bmatrix}
\]
\[\vec{x} =
\begin{bmatrix}
x_1\\
x_2\\
x_3\\
1 \\
\end{bmatrix}
\]
\[\overrightarrow{y_{隐藏层}}=\begin{bmatrix}
y_4 \\
y_5 \\
\end{bmatrix}
\]
推导输出层的前向传播
同理，可推出输出层的前向传播计算公式：
\[\overrightarrow{y_{输出层}}=f(W_{输出层}\cdot\overrightarrow{y_{隐藏层}})
\]
其中：
\[W_{输出层} = \begin{bmatrix}
\vec{w_6} \\
\vec{w_7} \\
\end{bmatrix} =\begin{bmatrix}
w_{64}, w_{65}, w_{b_6} \\
w_{74}, w_{75}, w_{b_7} \\
\end{bmatrix}
\]
\[\overrightarrow{y_{隐藏层}} =
\begin{bmatrix}
y_4 \\
y_5 \\
1 \\
\end{bmatrix}
\]
\[\overrightarrow{y_{输出层}}=\begin{bmatrix}
y_6 \\
y_7 \\
\end{bmatrix}
\]
推导后向传播
我们先来看下输出层的梯度下降算法公式：
\[w_{kj}=w_{kj}-\eta\frac{dE}{dw_{kj}}
\]
其中：\(k\)是输出层的节点序号，\(j\)是隐藏层的节点序号，\(w_{kj}\)是输出层的权重矩阵\(W_{输出层}\)的权重值，\(\frac{dE}{dw_{kj}}\)是节点k的梯度
设\(net_k\)函数是节点k的加权输入：
\[net_k=\overrightarrow{w_k}^T\cdot\overrightarrow{y_{隐藏层}} = \sum_{j} w_{kj}y_j
\]
因为\(E\)是\(\overrightarrow{y_{输出层}}\)的函数，\(\overrightarrow{y_{输出层}}\)是\(net_k\)的函数，\(net_k\)是\(w_{kj}\)的函数，所以根据链式求导法则，可以得到：
\[\begin{aligned}
\frac{dE}{dw_{kj}} & = \frac{dE}{dnet_k}\frac{dnet_k}{dw_{kj}} \\
& = \frac{dE}{dnet_k}\frac{d\sum_{j} w_{kj}y_{j}}{dw_{kj}} \\
& = \frac{dE}{dnet_k}y_{j} \\
\end{aligned}
\]
定义节点k的误差项\(\delta_k\)为：
\[\delta_k = \frac{dE}{dnet_k}
\]
因为\(y_{j}\)已知，所以只要求出\(\delta_k\)，就能计算出节点k的梯度
同理，对于隐藏层，可以得到下面的公式：
\[w_{ji}=w_{ji}-\eta\frac{dE}{dw_{ji}} \\
\frac{dE}{dw_{ji}} = \frac{dE}{dnet_j}x_{i} \\
\delta_j = \frac{dE}{dnet_j}
\]
其中：\(j\)是隐藏层的节点序号，\(i\)是输入层的节点序号，\(w_{ji}\)是隐藏层的权重矩阵\(W_{隐藏层}\)的权重值，\(\frac{dE}{dw_{ji}}\)是节点j的梯度
因为\(x_{i}\)已知，所以只要求出\(\delta_j\)，就能计算出节点j的梯度
推导输出层的\(\delta_k\)
因为节点k的输出值\(y_k\)作为\(\overrightarrow{y_{输出层}}\)的一个值，并没有影响\(\overrightarrow{y_{输出层}}\)的其它值，所以节点k直接影响了\(E\)。也就说
因为\(E\)是\(y_k\)的函数，\(y_k\)是\(net_k\)的函数，所以根据链式求导法则，可以得到：
\[\delta_k=\frac{dE}{dnet_k} = \frac{dE}{dy_k}\frac{dy_k}{dnet_k}
\]
上式的第一项等于：
\[\frac{dE}{dy_k} = \frac{dE(\overrightarrow{y_{输出层}})}{dy_k}
\]
上式的第二项即为求激活函数\(f\)的导数：
\[\frac{dy_k}{dnet_k} = \frac{df(net_k)}{dnet_k}
\]
将第一项和第二项带入\(\frac{dE}{dnet_k}\)，得到：
\[\delta_k = \frac{dE(\overrightarrow{y_{输出层}})}{dy_k}\frac{df(net_k)}{dnet_k}
\]
只要确定了\(E\)和激活函数\(f\)，就可以求出\(\delta_k\)
一般来说，\(E\)可以为\(softmax\)，\(f\)可以为\(relu\)
推导隐藏层的\(\delta_j\)
因为节点j的输出值\(y_j\)作为输出层所有节点的一个输入值，影响了\(\overrightarrow{y_{输出层}}\)的每个值，所以节点j通过输出层所有节点影响了\(E\)。也就说\(E\)是输出层所有节点的\(net\)的函数，每个\(net\)函数\(net_k\)都是\(net_j\)的函数，所以根据全导数公式，可以得到：
\[\begin{aligned}
\delta_j =\frac{dE}{dnet_j} & = \sum_{k\in{输出层}} \quad\frac{dE}{dnet_k}\frac{dnet_k}{dnet_j} \\
& = \sum_{k\in{输出层}} \quad\delta_k\frac{dnet_k}{dnet_j}
\end{aligned}
\]
因为\(net_k\)是\(y_{j}\)的函数，\(y_{j}\)是\(net_j\)的函数，所以根据链式求导法则，可以得到：
\[\begin{aligned}
\frac{dnet_k}{dnet_j} & = \frac{dnet_k}{dy_{j}}\frac{dy_{j}}{dnet_j} \\
& = \frac{d\sum_{j} w_{kj}y_{j}}{dy_{j}}\frac{dy_{j}}{dnet_j} \\
& = w_{kj}\frac{dy_{j}}{dnet_j} \\
& = w_{kj}\frac{df(net_j)}{dnet_j} \\
\end{aligned}
\]
代入，得：
\[\delta_j = \sum_{k\in{输出层}} \quad\delta_k w_{kj}\frac{df(net_j)}{dnet_j}
\]
只要确定了激活函数\(f\)和得到了每个\(\delta_k\)，就可以求出\(\delta_j\)
后向传播算法
通过上面的推导，得知要推导隐藏层的\(\delta_j\)，需要先得到出下一层（也就是输出层）每个节点的误差项\(\delta_k\)
这就是反向传播算法：需要先计算输出层的误差项，然后反向依次计算每层的误差项，直到与输入层相连的层
推导权重和偏移更新
经过上面的推导，可以得出输出层的更新公式为：
\[\begin{aligned}
w_{kj} =w_{kj}-\eta\delta_k y_j
\end{aligned}
\]
隐藏层的更新公式为：
\[\begin{aligned}
w_{ji} & =w_{ji}-\eta\delta_j x_i
\end{aligned}
\]
总结
我们在推导隐藏层的误差项时，应用了全导数公式，这是一个难点
参考资料
零基础入门深度学习 | 第三章：神经网络和反向传播算法
大家好~本文推导全连接层的前向传播、后向传播、更新权重和偏移的数学公式，其中包括两种全连接层：作为输出层的全连接层、作为隐藏层的全连接层
