多变量微积分笔记19——直角坐标系和柱坐标系下的三重积分
三重积分
三重积分由平面转到了空间，但本质上与二重积分一致。f(x,y,z)是空间函数，对应的三重积分是：
其中R区域是f在定义域范围内的图形的体积，dv是体积积元。在二重积分中，面积积元dA = dydx，三重积分的体积积元dv = dzdydx。
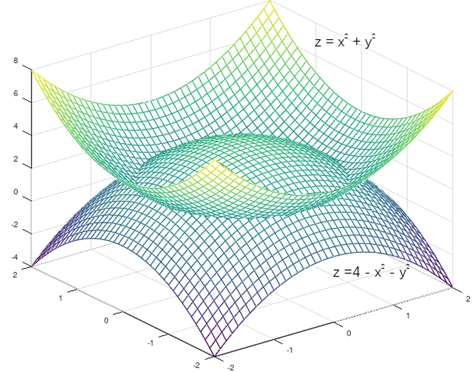
考虑计算两个曲面z = x2 + y2 和z = 4 – x2 – y2 围成的图形的体积。注意这里没有给出被积函数，两个曲面表示了积分域。
用三重积分表示所求体积，并用z作为最内层积分：
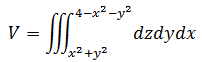
上式处理了z轴，剩下的是dydx，这就和二重积分一样了。现在需要关注的是所求曲面在xy轴上的投影，找出投影的边界值。
从两个曲面的方程可知，投影是圆，x和y的取值范围就是圆内的所有点，问题是如何求得圆的方程？
还是从所求曲面的图形入手，在这个曲面中z的范围已知，就是z轴的积分域：
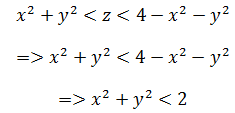
这就是x,y的取值范围，也就是半径为sqrt(2)的圆内的所有点。用二重积分表示圆的面积：
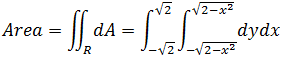
将Area和并到三重积分中：
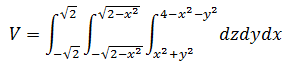
实际上对dz的积分是曲面的高度，dydx是面积，三重积分可以看做二者的乘法。
计算过程和二重积分类似，由内而外逐一计算：
柱坐标系
继续计算上一节的三重积分将得到复杂的式子，更好的方法是使用极坐标。首先保持dz不变，将dydx替换成极坐标（可参考《多变量微积分笔记9——极坐标下的二重积分》）：
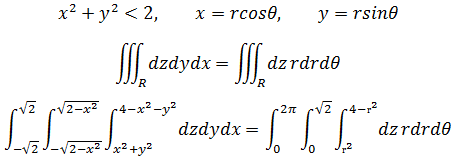
这种更简单的方法就称为柱坐标法。柱坐标的基本思想是在空间中建立一个点，用极坐标代替它的xy坐标，(r, θ, z)代替(x, y, z)，如下图所示：
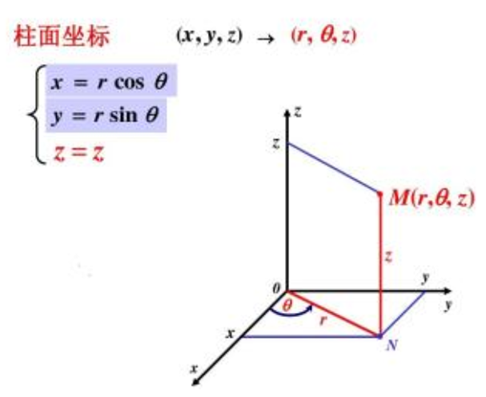
在柱坐标系中，积分将转换成：
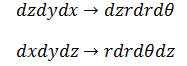
综合示例
示例1
计算单位球和z > 1 – y所围的曲面的体积。
将上图转换为“简笔画”——转换为平面坐标系：
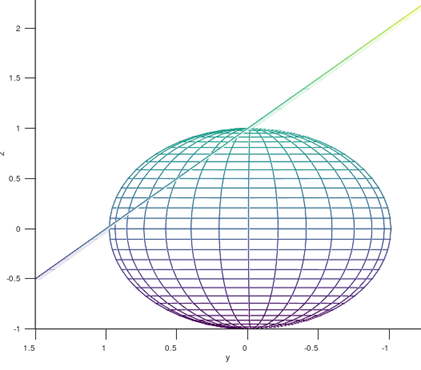
yz坐标系
容易得到z的积分域：
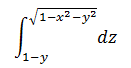
现在的问题是xy轴的投影是什么，即xy的积分域是多少？
由z的积分域可以得到不等式方程：
已知0 < y < 1，所以：
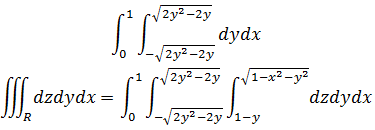
示例2
计算z = x2 + y2 和z = 2y所围的曲面的体积。
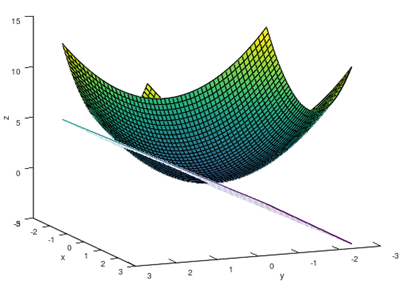
Z的积分域：
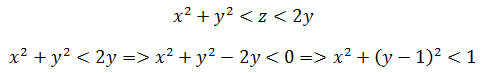
可见xy轴的投影是圆。由此可以使用柱坐标系：
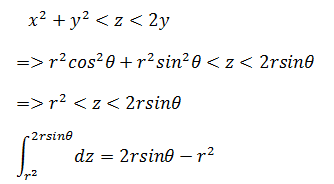
xy转换为极坐标后，0 ≤ θ ≤ π，rmin = 0，rmax是r关于θ的函数。
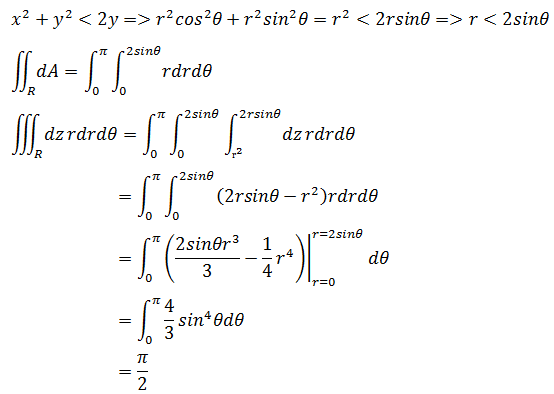
关于三角函数的积分计算可参考《数学笔记20——三角替换1（sin和cos）》
作者：我是8位的
