多变量微积分笔记8——二重积分

　　二重积分是二元函数在空间上的积分，同定积分类似，是某种特定形式的和的极限。本质是求曲顶柱体体积。重积分有着广泛的应用，可以用来计算曲面的面积，平面薄片重心等。平面区域的二重积分可以推广为在高维空间中的（有向）曲面上进行积分，称为曲面积分。

　　本篇涉及到的单变量积分的知识可参考《数学笔记13——定积分》

二重积分的意义

　　一元积分的被积函数是二维空间的曲线，其几何意义是计算曲线与x轴围成的面积；二重积分的被积函数是空间中的一个曲面，其几何意义是计算该曲面在xy平面的投影与该曲面围成的曲项柱体的体积。

　　一元函数y = f(x)，  ：

 

　　二元函数z= f(x,y)的积分：

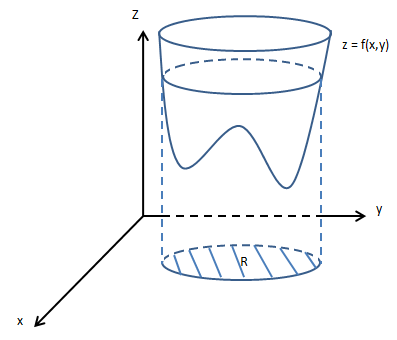
　　f(x,y)在xy平面的投影的区域是R，其二重积分称之为区域R上f(x,y)dA的二重积分，表示为：

 

　　dA表示R上的一小块面积。

用黎曼和计算体积

　　一元积分采用黎曼和分块，二重积分也是类似的思路，如下图所示：

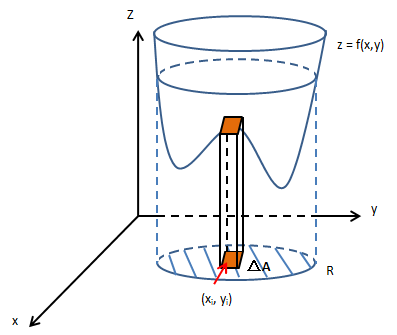
　　R区域分成了多个小块，每块的面积是ΔA。设第i块的面积是ΔA_i，ΔA_i中心点在xy平面对应的值是(x_i, y_i)，那么第i小块的高是f(x_i, y_i)，面积是f(x_i, y_i)ΔA_i：

 

　　这个式子对应三维空间中函数图像下方R区域内所有小柱体的体积之和。如果取积分，就是对所有小块面积ΔA取极限，使其趋近于0，就得到了二重积分：

 

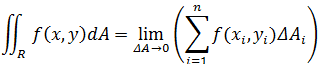
计算二重积分

计算方法的来源

　　在计算二重积分时，需要将一个二重积分的计算简化为两个单变量积分的计算，因此对于二重积分，所有在一元积分中的计算方法都适用。

 

　　如上图所示，平面T与xz平面垂直且与y轴平行，S(x₀)是绿色阴影部分的面积。如果将T沿x轴垂直方向前后移动（但不能超过R区域），将会得到不同的面积S(x)，将这些S(x)相加（做积分），就会得到柱体的体积：

 

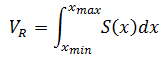
　　积分上下限就是平面T与R区域的切点。

　　现在的问题是如何计算S(x)？还是利用黎曼和的思想，将面积切割成小块，如下图所示：

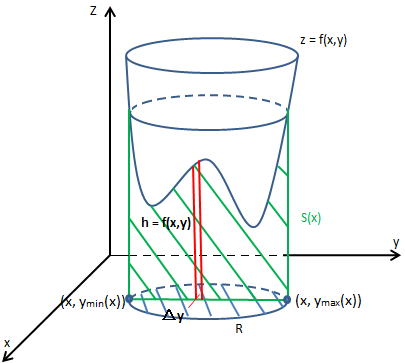
　　小矩形的宽度是Δy，高度是f(x,y)，对于给定的x来说，S(x) 实际上是关于变量y的积分：

 

　　积分域表示对于给定的切面S(x)，x是定值，y是随着x变化的。

　　现在把两个积分式合并在一起，就得到了二重积分：

 

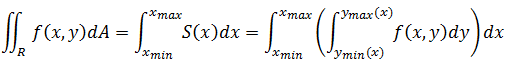
　　通常将最后一步的括号省略：

 

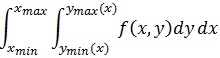
　　实际上二重积分就是累次积分，它做了两次积分，先固定x，对y积分（计算切面面积S(x)）；再固定y，对x积分（计算R区域的体积）。

　　在这里dA最终变成了dydx，这是因为将R区域的面积分成了无数个小矩形，矩形的长和宽就是dy和dx，小矩形面积dA = dydx，由此看来先对x积分和先对y积分是一样的。

计算的一般过程

　　计算二重积分的一般过程就是分步积分，下面是一个示例。

　　计算z = 1 – x² – y²在0 ≤ x ≤ 1，0 ≤ y ≤ 1上的积分。

　　重积分表达式是：

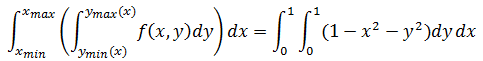
　　第一步是计算内积分，将x看作固定值，对y做积分：

 

　　经过第一步后，y将从结果中消失。接下来计算外积分：

 

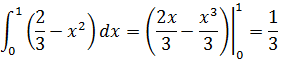
　　这就是最终答案了。

积分的边界

　　现在修改一下函数的定义域，如果约束 x² + y² ≤ 1且x ≥ 0，y ≥ 0，那么z的二重积分是什么？

　　如下图所示，R区域实际上是1/4圆：

　　现在以y为内积分，x为外积分，判断积分域。容易知道x的取值范围是 0 ≤ x ≤ 1，而y是受x约束的：

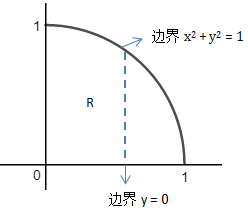
　　在虚线上，x是定值，y的边界是y = 0和x² + y² = 1，用x表示y就得到了内积分的边界值：

 

　　

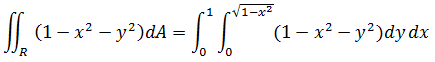
　　外积分使用三角替换（积分的三角替换可参考《数学笔记20——三角替换1（sin和cos）》），令x = sinθ，0 ≤ θ ≤ π/2，dx = cosθdθ：

 

 

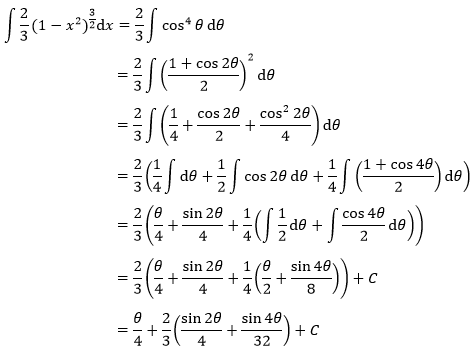
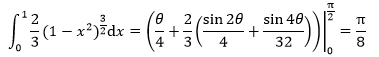
　　最终答案是π/8

改变内外积分的顺序

　　由于先对x积分和先对y积分是一样，所以在某些情况下可以通过改变内外积分的顺序来使计算更加简单。需要注意的是，交换后内外积分的积分域也要随之改变：

 

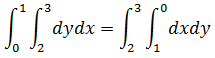
　　示例

　　 

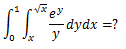
　　如果先计算内部积分，会发现很难，你会在第一步就卡住，无法继续计算，在这种情况下可以尝试改变内外积分的顺序。

　　改变顺序的时候要同时改变积分域，从原积分域中0 < x < 1,  x < y < x^1/2可以看出，0 < y < 1，所以：

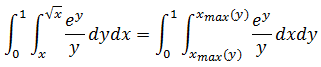
　　现在的问题是x如何受到y的影响？如下图所示，结合积分域，R区域就是y = x和y = x^1/2这两条曲线所围成的部分：

　　在图中容易看出x的两个边界，右边界（x上限）是y = x，左边界（x下限）是y = x^1/2。如果改写成x关于y的表达式，则右边界x = y，左边界x = y²，所以：

　　现在可以计算内部积分：

 

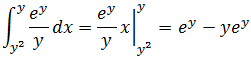
　　外部积分：

 

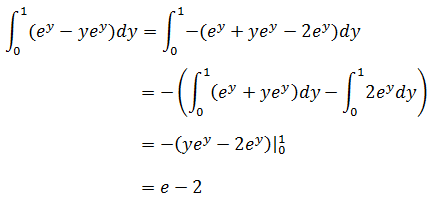
综合示例

示例1

　　如果R区域是(0,0), (0,2) , (-1,2)三点围成的三角形，求∫∫_Rdxdy和∫∫_Rdydx的积分域。

　　直角三角形就是R区域。

 

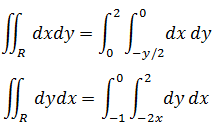
示例2

　　如果R区域是圆心在原点，半径为2的圆，直线y=x的下方， x轴的上方共同围成的，求∫∫_Rdxdy和∫∫_Rdydx的积分域。

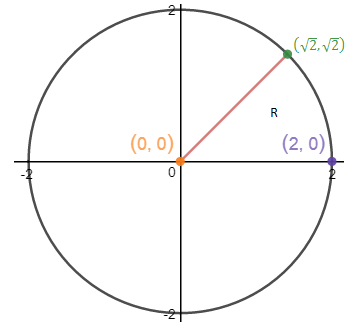
　　以y为外积分，dy的上下边界是0，2^1/2；需要思考的是内积分的上下边界。

　　如上图所示，在虚线上，y值固定，虚线上的左边界是y = x，右边界是圆x² + y² = 4，所以在虚线上，y < x < (4 - y²)^1/2，这就是内积分的边界。

 

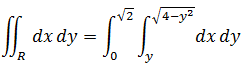
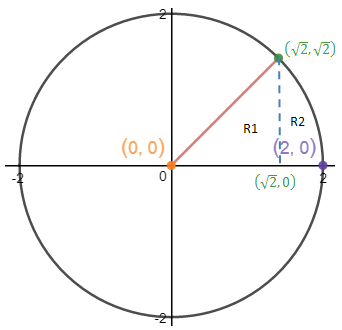
　　以x为外积分看起来似乎没那么容易，此时R区域需要分成两个部分，每个部分的内积分边界值是不同的：

 

示例3

　　计算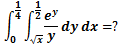

　　改变积分顺序可以简化问题。

　　R区域如下图所示：

 

 

 

---

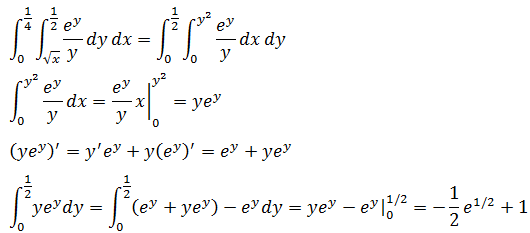
　　作者：我是8位的

　　出处：http://www.cnblogs.com/bigmonkey

　　本文以学习、研究和分享为主，如需转载，请联系本人，标明作者和出处，非商业用途！ 

　　扫描二维码关注公众号“我是8位的”