多变量微积分笔记6——拉格朗日乘数法
基本的拉格朗日乘子法(又称为拉格朗日乘数法)，就是求函数 f(x1,x2,...) 在 g(x1,x2,...)=C 的约束条件下的极值的方法。其主要思想是引入一个新的参数 λ （即拉格朗日乘子），将约束条件函数与原函数联系到一起，使能配成与变量数量相等的等式方程，从而求出得到原函数极值的各个变量的解。拉格朗日乘子是数学分析中同一名词的推广。
什么是拉格朗日乘数法
简单地说，拉格朗日乘数法是用来最小化或最大化多元函数的。如果有一个方程f(x,y,z)，在这个方程里的变量之间不是独立的，也就是说这些变量之间是有联系的，这个联系可能是某个方程g(x,y,z) = C；也就是g(x,y,z) = C定义了x,y,z之间的关系，这个关系对变量做出了一定的的限制，我们需要在这个限制下来最小化或最大化f(x,y,z)。
这里的最值不能简单地使用临界点，因为临界点通常不满足关系方程g。如何解决这个问题呢？当这个限制g(x,y,z)非常简单的时候，我们可以解出其中一个变量的表达式，把这个表达式代入f(x,y,z)后求得最值，这也是中学阶段常用的方法。但问题是，很多时候我们并不能解出x,y,z，因为关系方程g太复杂了，这就需要一个全新的方法求解，拉格朗日乘数法就是其中一种。
寻找最值
示例：找出双曲线xy = 3上离原点最近的点。
如果(x, y)是曲线上的点，原点到该点的距离是：
求离原点最近的点实际上是求f(x,y)的最小值。可以使用一个更容易的方程去掉根号：
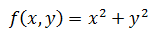
在计算最小值时候有一个限制是：
把这个较为简单的例子用等高线图表示：
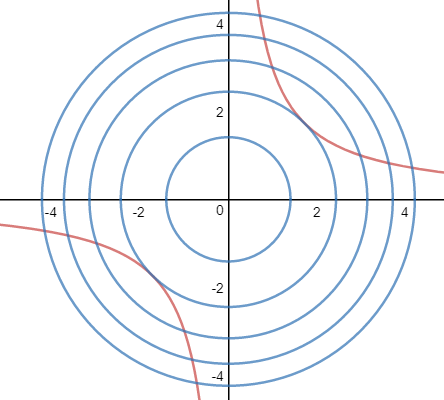
很明显，当f和g相切的时候，能得到f的最小值。如果把双曲线看作自身的等高线，那么当f的等高线和g的等高线相切时，f值最小。实际上这也是找到最值的一般情形。
如果两个等高线相切，则二者在切点处的切线也相同，也就是说它们的梯度向量平行，即：
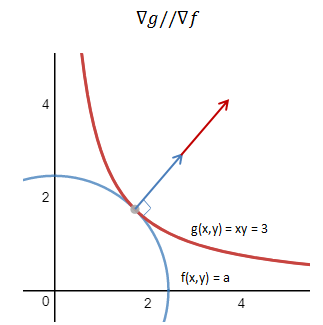
如果两个向量平行，则其中一个向量是另一个向量的倍数，由此得到：
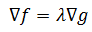
这里的λ是一个常数，我们需要做的是找到这个λ和特定的(x,y)使得上式成立。这实际上是把2个变量加一个关系限制的最值问题转换为一个含有3个变量的方程组。
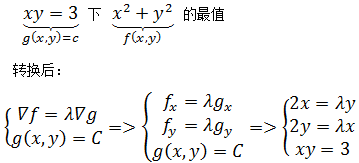
现在已经通过梯度向量平行，将原来的最值问题转换为一般的方程组，这个方程组被称为拉格朗日方程组，它的解就是最值点。
接下来就是解方程组，可以将其看作是关于xy的矩阵方程：
一个满足方程组的解是x = 0, y = 0，但这个解不满约束条件g(x,y) = xy = 3；此外，只有当系数行列式的值是0时，方程才有多个解：
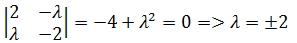
把两个值分别代入方程组：
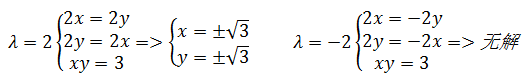
现在可以回答原问题，双曲线xy = 3距离原点最近的点有两个：(31/2, 31/2)和(-31/2, -31/2)。
在这个例子中，λ就是拉格朗日乘子。
最小值和最大值
拉格朗日乘数法并不会告诉我们最值的类型，结果可能是最大值、最小值或鞍点，由于存在限制条件，这里也不能像《多变量微积分3——二元函数的极值》那样使用二阶导数判断。那么如何判断是最大值还是最小值呢？只能通过将拉格朗日方程组的解代入问题方程f来判断。举例来说，如果有三组解，代入f后分别是4,6,9，在不存在边界值时，4就是最小值，9就是最大值；如果存在边界，还需要比较边界值。在双曲线的例子中，由于能够确定边界在无穷远处，所以其结果就是最小值。
表面积最小的金字塔
给定金字塔的体积和底面积（底面的三边确定，分别是a1,a2,a3），如何建造一个表面积最小的金字塔？
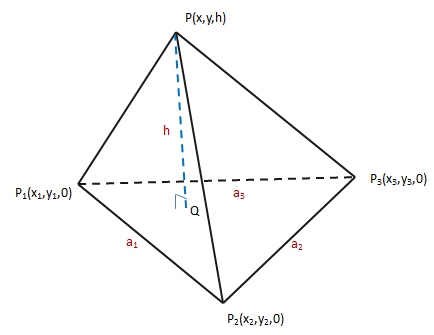
如上图所示，将金字塔模型放入三维坐标系中，底面对应xy轴。由于体积和底面积已知，根据体积公式，高也是定值，那么实际问题就是回答Q点的位置。一种思路是利用向量的叉积计算三角形的面积（参考《线性代数笔记4——向量3（叉积）》）：
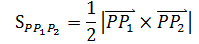
展开后将得到一个很长的式子，看起来并不是什么好方法。现在换一种思路，利用三角形面积的几何公式，如下图所示：
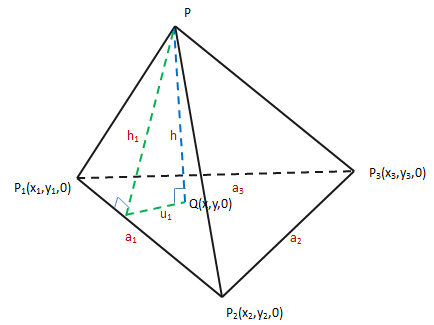
h1是三角形PP1P2的高，设点Q是(x,y,0)，则：
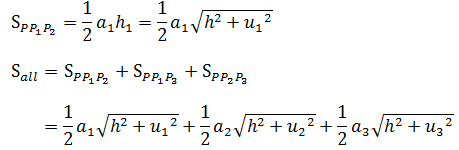
这就转换成了有三个变量的函数，目标是求得f的最小值：
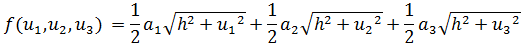
接下来需要寻找约束条件g。由于a1⊥h1且a1⊥h，所以a1垂直于h1和h所在的平面，a1⊥u1。
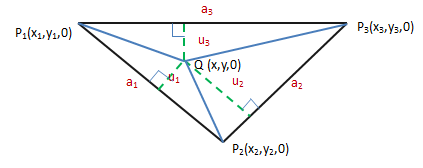
上图可知：
这就是约束条件g：
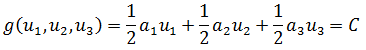
知道了f和g，就可以使用拉格朗日乘数法：
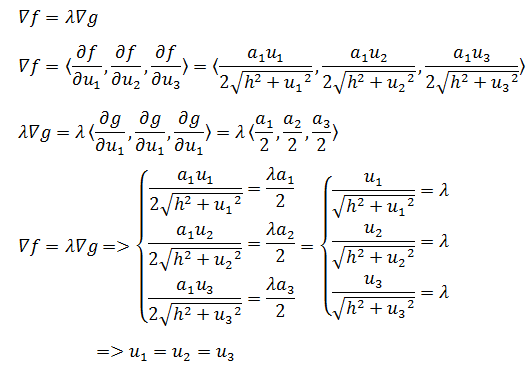
当Q点的位置距离三边距离相等时，金字塔的表面积最小。
备注：
f对u1偏导将u2和u3看作常数，这相当于求f(u)的导数，
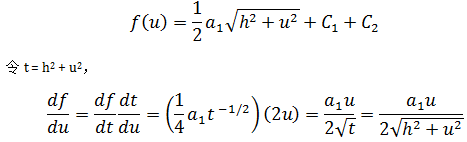
综合示例
示例1
在椭圆x2 + 4y2 = 4中有内接的矩形，该矩形的边平行于x轴和y轴，找出这些矩形中周长最大的一个。
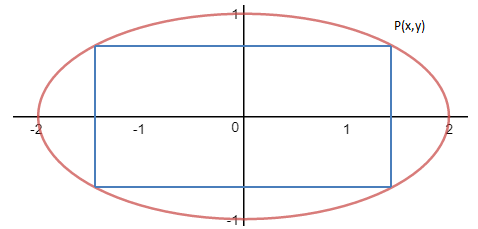
如上图所示，长方形的周长函数是f(x,y) = 4x + 4y，约束函数g(x,y) = x2 + 4y2 = 4
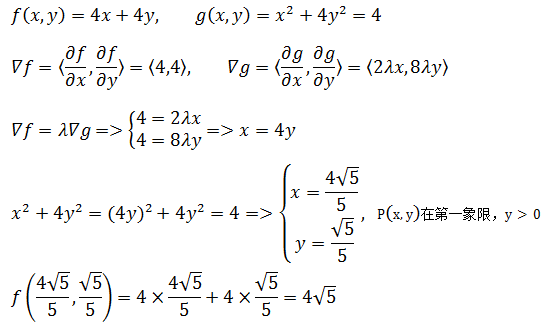
由于拉格朗日乘数法无法确定最值的类型，所以还要对函数边界进行计算。当P在椭圆上移动时，如果正好落在x轴上，则长方形退化成直线，此时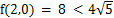 
；另一个极值是
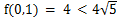，所以判定
是最大值，此时长方形的一点的坐标是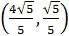
示例2
计算f(x,y,z)= x2 + x + 2y2 + 3z2在约束条件x2 + y2 + z2 = 1下的最值。
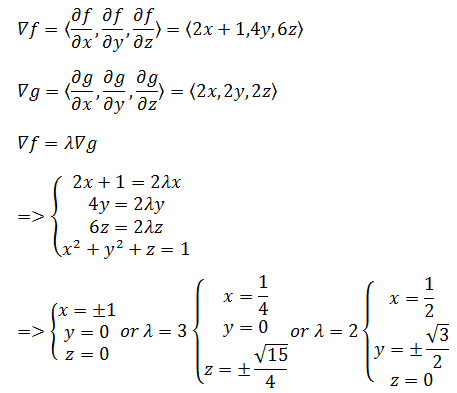
由于约束条件是球体，所以不存在边界，只需把这些解导入f即可。当点在(-1,0,0)时，f最小，f = 0；当点在(1/4,0,±151/2/4)时f最大，f = 25/8
出处：微信公众号 "我是8位的"
本文以学习、研究和分享为主，如需转载，请联系本人，标明作者和出处，非商业用途！
扫描二维码关注作者公众号“我是8位的”
