闲话复数(1) | 不现实的虚数 i 为什么虚?它长成什么样?
原文 | https://mp.weixin.qq.com/s/y-Nb3S508UZuf_0GtRuNaQ
复数的英文是complex number,直译是复杂的数。最早接触复数大概是在高中时期,只知道复数由实部和虚部组成,虚部用i表示,i2=-1。天啊,无限不循环的无理数勉强可以接受,这个i到底是个什么东西?相比实数而言,这个不现实的虚数为什么虚?它长成什么样?
虚数的诞生
当年老师并没有拿出某个东西说:“看,这就是虚数!”当然拿不出来,我们很难形象化地表现这些不现实的虚数。
16世纪意大利米兰数学家卡尔达诺(Jerome Cardan,1501—1576)曾经讨论过一个问题:是否可能把10分成两个数,使它们通过各种数学运算得到40(我真是很难理解数学家的大脑,究竟是基于什么原因让他们思考这个问题?为了是打赌吗?)。卡尔达诺把答案写成:
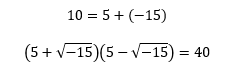
尽管卡尔达诺认为-15的平方根是没有意义的、想象的、虚无飘渺的,但他还是这么写了,他也因此成为第一个把负数的平方根写到公式中的数学家。真正给出“虚数”这一名称的是法国数学家笛卡尔(1596—1650),他在《几何学》(1637年发表)中使“虚的数”与“实的数”相对应,从此,虚数才流传开来。
在求解x2=2的过程中,人们定义了无理数√2,这个从有理数扩展的来的概念让我们能够在更广的范围内进行代数运算。同样,x2=-1也提出了一个类似的问题。不过由于没有任何实数的平方等于-1,所以早期的数学家都认为这个方程是没有意义的,把它和除数不能等于0一样处理。随着时间的推移,这种方程出现的越来越多,人们逐渐意识到,让这类方能够继续计算下去是有意义的,于是定义了一种超自然的符号解,对于实数(Real number)来说,这个数是虚拟的,是想象中的,它就是虚数(imaginary number)i。
有了虚数,就可以对一个负数开平方,这使得“把一个数开根号再平方”可以运用在更大的范围上,卡尔达诺把答案也就成立了:
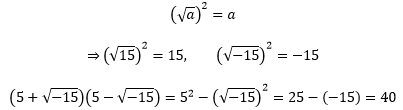
复数
在数学上,虚数和实数有着同等地位,二者合在一起成为复数。一个复数由实部和虚部组成,用z=a+bi表示,其中a,b是任意实数。如果一个复数只有虚数部分,则称这个复数是纯虚数。很多时候复数和虚数会互相混用,有很多资料把z=a+bi (a≠0)叫做虚数。如果较真一点,a+bi是复数,a是复数的实部,b是复数的虚部,i是虚数。
实数中的交换律、结合律、分配律可以很自然地扩展到复数的加法和乘法上,于是一种符合情理的计算方式被定义出来了:
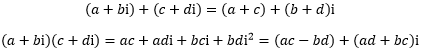
上面的一切还较为自然,但是面对除法时,问题出现了:两个纯虚数的除法可以很容易计算,但是两个同时存在实部和虚部的复数又怎么计算除法呢?接着计算的办法就是继续定义新的概念。
共轭复数
先解释一下共轭复数(conjugate complex number)。“轭”的本意是两头牛背上的架子,”轭“使两头牛同步行走。共轭是指按一定的规律相配的一对东西,一个架子上的两头牛互为共轭牛,来个共轭看看:

两个实部相等,虚部互为相反数的复数互为共轭复数。当虚部不为零时,它的共轭复数就是实部相等,虚部相反;如果虚部为零,其共轭复数就是自身。复数z的共轭复数用z上面加一横表示。
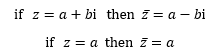
这个奇怪的共轭复数来自复平面,有很多非常好的性质(在介绍复平面时会再次讨论),其中一个性质是,互为共轭的两个复数的乘积是实数:
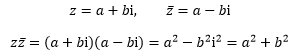
是不是跟“负负得正”有点像(这里是”复复得实“)?
复数的除法
有了共轭复数,就可以定义两个复数的除法运算规则:将分子和分母同时乘以分母的共轭复数。
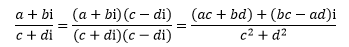
乘法和除法互为逆运算,复数也一样:
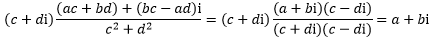
复数的大小
给出两个实数,我们总是能比较它们的大小,然而对于复数来说,比较大小并没有想象的那么简单,事实上,复数无法进行除了相等外的大小比较。
比较关系是和加法或乘法相容的,比如有3个实数a,b,c,如果a > b,一定有a+c > b+c;如果c >=0,一定有ac > bc。可是到了复数这里完全不是这么回事,以虚数 i 为例,我们只知道它的平方等于-1,但是这玩意到底和0有什么关系?如果定义i > 0,好了,两个大于0的数相乘应该还是大于0,但 i2 却等于-1;如果定义i < 0,负负得正,i2却偏偏不得正;如果定义 i = 0,那要它何用,直接用0不就好了,干嘛还要定义这玩意?既然虚数比较不了大小,那么包含虚部的复数也一样比较不了大小:一个实数加上一个不知道谁大谁小的虚部,天知道得出的结果究竟是比原来大还是比原来小!
现在思路切换。
(1,1)和(2,2)是平面上的两个向量,我们知道向量是表示大小和方向的量,但从来没写过(1, 1) < (2, 2),向量的模才有大小:
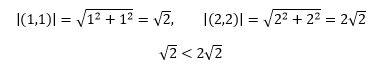
这似乎在告诉我们,超过一维的东西没法直接比较大小,想要比较大小的话,必须通过某种方式转换成一维。你可能会产生疑问了,两个平面几何图形我一眼就能看出谁大谁小,怎么说二维的东西不能比较呢?没错,很多时候确实能够一眼看出来谁大谁小,确切地说是看出面积谁大谁小,A = <a1, a2>,B = <b1, b2>,A、B围成的面积咋算?
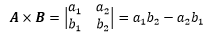
这是叉积对吧?等于一个行列式对吧?行列式最终能算出一个数值对吧?这个数值是一维的对吧?
空间图形也一样,我们可以度量以三个向量为临边的平行六面体的体积,最终还是能算出一个数值,A = <a1, a2, a3>,B = <b1, b2, b3>,C = <c1, c2, c3>:
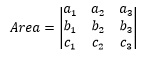
n维空间也一样,我们可以度量n维图形在n维空间中的n维体积。
回到复数问题上,复数之所以没法比较大小,是因为复数跟实数本来就不在一个维度,复数本身就是一个二维的数。
复平面
笛卡尔发明了坐标系,从此之后让代数和几何联系在一起。既然复数是一个二维的数,我们就可以考虑用一个平面来表示它,这个特殊的平面就是复平面。在复平面中,z=a+bi 对应的坐标为(a,b) 。其中a表示的是复平面内的横坐标,在x轴(实轴)上;b表示的是复平面内的纵坐标,在y轴(虚轴)上;y轴上有且仅有的一个实点是原点。
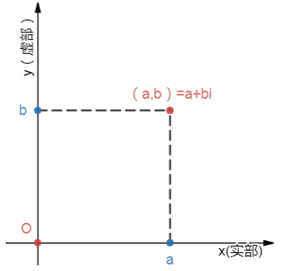
复数的模
平面向量有模长,复数是二维的,同样可以定义模长。对于z=a+bi来说,它的模长是:
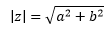
这跟向量没啥区别,几何意义就是复平面上点到原点的距离:
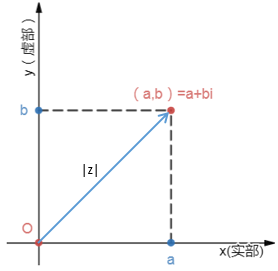
再看共轭复数
前面说过,a+bi 的共轭复数是a-bi,现在把共轭复数放到复平面内:
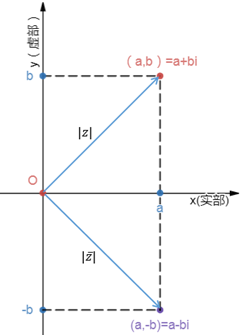
还真像一根棍子上的两头牛。
模是标量,两个互为共轭的数的模相等,两个共轭数相乘的结果是其中一个数的模的平方:
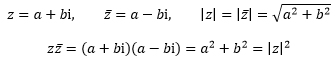
乘法的意义
我们很容易在复平面上定义复数的加法和数乘,它们都和向量类似。如果复平面上有两个复数(x1, y1)和(x2, y2),二者相加的结果是(x1 + x2, y1 + y2)。对于复数的乘法,我们先给出代数结果:
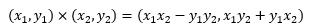
其实这个公式的来源就是两个复数的乘法运算:
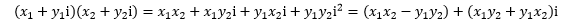
它的好处在于把所有关于 i 的信息都去掉了,或者说把 i 当成了普通的实数,确切地说是二维的实数:
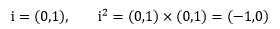
i2最终变成了(-1,0),在复平面上是一个点,该点的实轴坐标是-1,虚轴坐标是0,因此我们可以说 i=(0,1), -1=(-1, 0)。这个规则同样适应于实数:
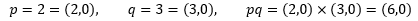
现在问题是,如何在复平面表示两个复数的乘法?
先简单一点,用一个复数乘以一个实数:
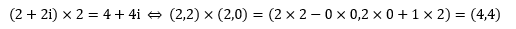
它的几何意义是把原复数沿着原来的方向延伸2倍:

同理,如果乘以-2,相当于把原复数沿着原来的相反方向延伸2倍,或者说绕源点逆时针旋转180°:
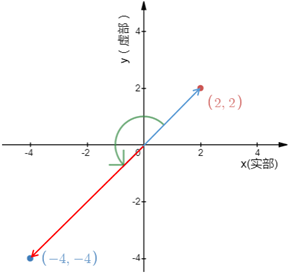
接下来用一个复数乘以一个纯虚数:
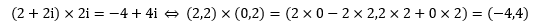
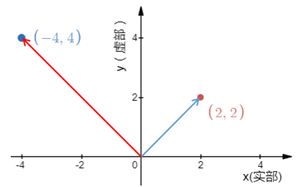
这是把(2, 2i)沿着原点逆时针旋转90°,然后再拉长2倍。
旋转告诉我们,用极坐标表示复数也许更为简单。在极坐标下,用模长和角度表示一个点:
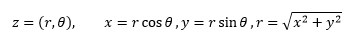
再看两个复数的乘法:
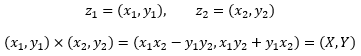
现在把结果转换成极坐标,这里利用一点三角函数的和差角公式:

这就又回到了极坐标和直角坐标的转换公式,因此,两个复数相乘是z1z2=(X,Y),用极坐标表示的话:
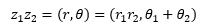
上式翻译成人话是说,在极坐标下,一个复数乘以另一个复数(r, θ),那么原复数的模长将拉伸r倍(r可以小于1,也可以是0或负值),并且逆时针旋转θ(θ可以是0也可以是负值,如果是负值的话就变成了顺时针旋转θ),这就是两个复数相乘的几何意义。
现在来看一个乘法:
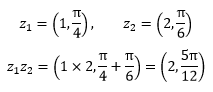
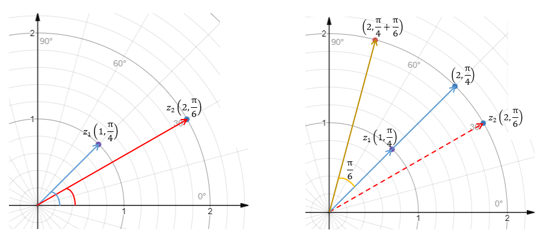
左图是极坐标下两个原始的复数,右图表示z1先拉伸2倍,再逆时针旋转π/6,得到z1z2。注意极坐标的两个箭头代表的是方向,而不是实部或虚部。
复平面使得复数变得简单,用笛卡尔坐标系表示复数加法的意义,用极坐标系表示复数乘法的意义,这为我们进一步探索复数打下了基础。
好吧,现在知道了复平面,这有什么用呢?且看下回分解。
作者:我是8位的
出处:https://mp.weixin.qq.com/s/y-Nb3S508UZuf_0GtRuNaQ
本文以学习、研究和分享为主,如需转载,请联系本人,标明作者和出处,非商业用途!
扫描二维码关注作者公众号“我是8位的”



 浙公网安备 33010602011771号
浙公网安备 33010602011771号