概率笔记7——数学期望
如果知道一个随机变量的分布函数，就能知道这个随机变量体现出的随机性的客观规律。但是很多时候我们不清楚分布函数是什么。有些时候，对于一批数据来说，未必一定要关心分布函数。比如一批产品，我们可能只关心这批产品的平均使用寿命，这里的平均使用寿命是随机变量的某个数字指标，称为随机变量的数字特征。数字特征与“随机”没有任何关系，确切地说是通过一系列计算方法将变量的随机性消除了。
数学期望的概念
数学期望是一种重要的数字特征，它反映随机变量平均取值的大小，是试验中每次可能结果的概率乘以其结果的总和。这里的“期望”一词来源于赌博，大概意思是当你下注时，期望赢得多少钱。
简单地说，数学期望就是均值，我们以一个例子来说明数学期望。
有一个射击比赛，分为大、中、小三类目标，其分值和命中率如下：
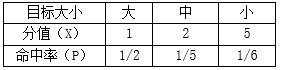
如果一个选手射击了三次，假设它一定会命中目标，那么期望的平均分是多少？
这个“期望的平均分”就是一个数学期望，看起来挺简单：
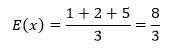
很遗憾，这是错误的结果，它忽略的命中率。正确的均值是：
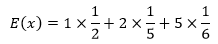
命中率相当于计算机算法中常说的权重（权重等同于概率论中的概率），通过加权平均才能得到合理的均值。因此说，数学期望就是合理的加权平均值，期望体现在合理二字上，期望值并不一定包含在变量的输出值集合里。
离散型和连续型随机变量的数学期望
离散型的数学期望容易理解，离散事件的每个取值都对应一个概率：
可以把xi看作得分，pi相当于得到该分值的概率，它的数学期望是所有变量的加权平均：
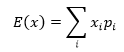
对于连续型事件来说，某一点的概率是没有意义的（详细说明参见上一章的内容），我们要关注的是某两个点之间的分布。实际上我们可以借助密度函数表达某一点上的概率。设f(x)是连续型事件的密度函数，那么P(x)=f(x)dx，虽然计算f(x)dx没有意义，也无法计算，但是并不妨碍用它来表达P(x)。现在知道了某一变量的值和该变量下事件发生的概率（权重），可以计算它的数学期望（加权平均）了：
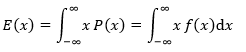
随机变量函数的数学期望
有一个随机变量X，Y=g(X)，Y的数学期望是什么？
g(X)是将随机变量包裹在一个函数内，这似乎有些令人迷惑，我们仍然以射击的例子说明。
之前的射击比赛得分太低，组织方打算提高分值，具体做法是在原来的分值基础上乘以100，即g(x) = 100x：
现在的目标是计算g(X)的数学期望。这次没那么难以理解了：
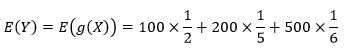
虽然得分变了，但命中率未变，也就是每个变量出现的概率没有变。将问题泛化，如果X是离散型随机变量，那么随机变量函数Y=g(X)的数学期望是：
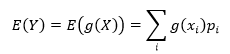
如果X是连续型随机变量，那么随机变量函数Y=g(X)的数学期望是：
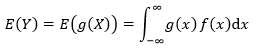
其中f(x)dx仍然相当于X=x时事件发生的概率P(x)。
数学期望的性质
设C为一个常数，X和Y是两个随机变量，则：
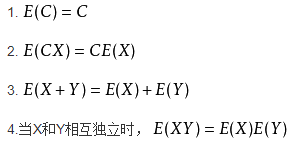
性质1是说期望是作用在随机变量上的，对常数无效；性质3和性质4可以推到到任意有限个相互独立的随机变量之和或之积的情况。
作者：我是8位的
