模拟赛第三学期

9.20

You have no egg！

9.21

100+100+100+0=300pts。

T1

给两个矩阵 \(A,B\)，对 \(A\) 的任意子方阵进行对称变换任意次，能否变成 \(B\)?

显然只需进行黑白染色即可，注意特判哦：）。

T2

给一个 01 串和一个字符串，第 \(i\) 个 1 会把 \(0-i\) 翻转，求最后的字符串。

自己维护一下后缀就行，当然可以用文艺平衡树。

T3

P10647

贪心即可，证明不会。

用大根堆即可优化到 \(O(n \log k)\)。

T4

P9000

扫码猎奇线段树。

9.25

0+0+0+0=0pts

评测事故，第一次爆零，纪念一下。

实际 100+20+100+0=220pts，rk1.

T1

纯爆搜，但是不好写，因为我太菜了。

T2

神秘 DP，只会暴力。

T3

P10065

结论题，猜到是平面图即可使用并查集通过。

T4

不会。

10.4

45+100+0+20=165pts，rk6。

怒挂 75pts，被所有人打爆。

T1

有三个罗盘，周期分别为 \(p_1,p_2,p_3\)，初始指针所处的位置分别为 \(r_1,r_2,r_3\)。
每次操作可以选择两个罗盘，将它们的指针同时向后挪移一位。当某个罗盘的指针位置达到它的周期时，它就
重新回到了位置 \(0\)。
求至少需要多少次操作才能将三个罗盘的指针都挪到 \(0\)。

若无法实现，报告无解。

列几个方程，然后爆搜，注意限制条件。

可以循环枚举的千万不要乱 bfs！千万不要乱特判！

#include<bits/stdc++.h>
#define int long long
#define gc getchar
#define pc putchar
#define rg register
#define LB lower_bound
#define UB upper_bound
#define PII pair<int, int>
#define PDI pair<double, int>
#define PID pair<int, double> 
#define fi first
#define se second
#define IOS ios::sync_with_stdio(0);cin.tie(0);cout.tie(0);
using db=double;using ll=long long;
using ull=unsigned long long;
using namespace std;
const ll INF=1e18;
const int inf=0x3f3f3f3f;
namespace IO{
	inline int read(){
		int x=0,f=1;
		char ch=gc();
		while(!isdigit(ch)){
			if(ch=='-') f=-f;
			ch=gc();
		}
		while(isdigit(ch)) x=(x<<3)+(x<<1)+ch-'0',ch=gc();
		return x*f;
	}
	inline void write(int x){
		if(x<0) pc('-'),x=-x;
		if(x>9) write(x/10);
		pc(x%10+'0');
	}
}using namespace IO;
int p1,r1,p2,r2,p3,r3;
int ans=inf;
inline int A(int x1, int x2, int x3){
	return p1*x1-p2*x2+p3*x3-(r1+r3-r2);
}
inline int B(int x1, int x2, int x3){
	return p1*x1+p2*x2-p3*x3-(r1-r3+r2);
}
inline int C(int x1, int x2, int x3){
	return -p1*x1+p2*x2+p3*x3-(r3+r2-r1);
}
signed main(){
//	freopen("114514.in","r",stdin);
//	freopen("114514.out","w",stdout);
	p1=read(),r1=read(),p2=read(),r2=read(),p3=read(),r3=read();
	for(rg int i=0;i<=500;i++){
		for(rg int j=0;j<=500;j++){
			for(rg int k=0;k<=500;k++){
				int a=A(i,j,k),b=B(i,j,k),c=C(i,j,k);
				if(a>=0&&b>=0&&c>=0&&a%2==0&&b%2==0&&c%2==0){
					ans=min(ans,(a+b+c)/2);
				}
			}
		}
	}
	if(ans==inf) puts("Help Me, Mr. ShenJun!");
	else write(ans);
	return 0;
}

T2

求

\[\sum_{k=0}^m \binom{n-k}{m-k} \binom{r+k}{k} \]

对 \(998244353\) 取模。

赛时猜出答案于是通过。

具体推导：

首先有（上指标翻转）：

\[\binom{r}{k}=(-1)^k \binom{k-r-1}{k} \]

于是：

\[\sum_{k=0}^m \binom{n-k}{m-k} \binom{r+k}{k} \]

\[=\sum_{k=0}^m (-1)^{m-k} \binom{m-n-1}{m-k} (-1)^{k} \binom{-r-1}{k} \]

\[=(-1)^m \sum_{k=0}^m \binom{m-n-1}{m-k}\binom{-r-1}{k} \]

根据范德蒙德卷积：

\[=(-1)^m \binom{m-(n+r+1)-1}{m} \]

翻转回来：

\[=\binom{n+r+1}{m} \]

T3

暴力 30pts 不写是人？

原题 P4757。

考虑 DP，设 \(f_i\) 为 \(i\) 子树最多能选的路径数，那么对于 \(LCA(u,v)=i\)，\(f_i=f_u+f_v+1\) 再加上路径内点的贡献。

但是并不好转移，因为还要考虑路径 \((u,v)\) 上的边没被选过，注意到一个点的度数最多为 \(10\)，于是考虑状压枚举选取边的集合，这个复杂度是 \(3^{10}\)。

然后再考虑路径内的点的贡献，可以考虑把 \(u \rightarrow i\) 的贡献加到 \(u\) 子树内，这样下次选取 \(u\) 子树内的起点，这些贡献也会被算进去，子树加单点查可以用树状数组维护。总时间复杂度为 \(O(3^{10}n+(m+n)\log n)\)。

#include<bits/stdc++.h>
#define int long long
#define gc getchar
#define pc putchar
#define rg register
#define LB lower_bound
#define UB upper_bound
#define PII pair<int, int> 
#define PDI pair<double, int>
#define fi first
#define se second
#define IOS ios::sync_with_stdio(0);cin.tie(0);cout.tie(0);
using db=double;using ll=long long;
using ull=unsigned long long;
using namespace std;
const ll INF=1e18;
const int inf=0x3f3f3f3f;
namespace IO{
	inline int read(){
		int x=0,f=1;
		char ch=gc();
		while(!isdigit(ch)){
			if(ch=='-')	f=-f;
			ch=gc();
		}
		while(isdigit(ch)) x=(x<<3)+(x<<1)+ch-'0',ch=gc();
		return x*f;
	}
	inline void write(int x){
		if(x<0) pc('-'),x=-x;
		if(x>9)	write(x/10);
		pc(x%10+'0');
	}
}
using namespace IO;
const int N=1e3+10;
const int M=(1<<10)+10;
int n,m,dp[N],g[M],id[N];
vector<int> e[N];
vector<PII> q[N];
int tim,f[N],dep[N],son[N],size[N],dfn[N],top[N];
namespace BIT{
	int tree[N];
	inline int lbt(int x){return x&-x;}
	inline void Clear(){for(rg int i=0;i<=n;i++) tree[i]=0;}
	inline void add(int x, int d){while(x<=n) tree[x]+=d,x+=lbt(x);}
	inline int query(int x){int res=0;while(x>0){res+=tree[x],x-=lbt(x);}return res;}
}using namespace BIT;
inline void init(){
	tim=0;
	for(rg int i=0;i<=n;i++){
		e[i].clear(),q[i].clear();
		dp[i]=f[i]=son[i]=dep[i]=0;
	}
	Clear();
}
inline void dfs1(int u, int fa){
	dep[u]=dep[fa]+1,size[u]=1,f[u]=fa;
	for(int v:e[u]){
		if(v==fa) continue;
		dfs1(v,u);size[u]+=size[v];
		if(!son[u]||size[son[u]]<size[v]) son[u]=v;
	}
}
inline void dfs2(int u, int tp){
	dfn[u]=++tim,top[u]=tp;
	if(!son[u]) return;
	dfs2(son[u],tp);
	for(int v:e[u]) if(v!=f[u]&&v!=son[u]) dfs2(v,v);
}
inline int LCA(int x, int y){
	while(top[x]!=top[y]){
		if(dep[top[x]]<dep[top[y]]) swap(x,y);
		x=f[top[x]];
	}
	return dep[x]<dep[y]?x:y;
}
inline void DP(int u, int fa){
	int tot=0;
	for(int v:e[u]) if(v^fa) DP(v,u);
	for(int v:e[u]) if(v^fa) id[v]=tot++;
	for(rg int i=0;i<(1<<tot);i++) g[i]=0;
	for(int v:e[u]) if(v^fa) g[1<<id[v]]=dp[v];
	for(auto p:q[u]){
		int qu=p.fi,qv=p.se;
		int zu=0,zv=0;
		if(qu^u){
			for(int v:e[u]){
				if(v==fa) continue;
				if(dfn[v]<=dfn[qu]&&dfn[qu]<=dfn[v]+size[v]-1) zu=(1<<id[v]);
				if(zu) break;
			}
		}
		if(qv^u){
			for(int v:e[u]){
				if(v==fa) continue;
				if(dfn[v]<=dfn[qv]&&dfn[qv]<=dfn[v]+size[v]-1) zv=(1<<id[v]);
				if(zv) break;
			}
		}
		g[zu|zv]=max(g[zu|zv],dp[qu]+dp[qv]+query(dfn[qu])+query(dfn[qv])+1);
	}
	for(rg int i=0;i<(1<<tot);i++)
		for(rg int j=i;j;j=(j-1)&i) g[i]=max(g[i],g[j]+g[i^j]);
	dp[u]=g[(1<<tot)-1];
	for(int v:e[u]){
		if(v==fa) continue;
		int sum=g[((1<<tot)-1)^(1<<id[v])];
		add(dfn[v],sum),add(dfn[v]+size[v],-sum);
	}
}
inline void Ruby(){
	n=read();init();
	for(rg int i=1;i<n;i++){
		int u=read(),v=read();
		e[u].push_back(v);
		e[v].push_back(u);
	}
	dfs1(1,0);dfs2(1,1);
	m=read();
	for(rg int i=1;i<=m;i++){
		int u=read(),v=read();
		q[LCA(u,v)].emplace_back(u,v);
	}
	DP(1,0);
	write(dp[1]),puts("");
}
signed main(){
//	freopen("114514.in","r",stdin);
//	freopen("114514.out","w",stdout);
	int T=read();
	while(T--) Ruby();
	return 0;
}

T4

20pts，写太史了，本来 40pts。

CF1601F。

10.5

100+100+20+0=220pts，rk3，罚时惨败 ycy 和 hlc。

rk3 为何 rating-503？看来他们 rating 都是从我这扣的。

T1

爆搜，难度大概 PJT3 左右。

T2

原题

是这个的简单版，只用算一个 \(k\)，不必使用 NTT。

考虑每个点对答案的贡献，钦定 \(1\) 为根，每个点对答案的贡献为：

\[\binom{n}{k}-\binom{n-size_u}{k}-\sum_{(u,v) \in E} \binom{size_v}{k} \]

这个东西 \(O(n)\) 就可以计算。

再看原题，现在考虑去统计每个点为根的情况，那么 \(u\) 对 \(f(k)\) 的贡献为:

\[\binom{n}{k}-\sum_{(u,v) \in E} \binom{size_v}{k} \]

于是

\[f(k)=n\binom{n}{k}-\sum_{u=1}^n \sum_{(u,v) \in E} \binom{size_v}{k} \]

拆贡献，设 \(c_i\) 为子树大小为 \(i\) 的子树的数量，

\[f(k)=n\binom{n}{k}-\sum_{i=1}^nc_i \binom{i}{k} \]

\[=n\binom{n}{k}-\frac{1}{k!}\sum_{i=1}^n\frac{c_i i!}{(i-k)!} \]

令 \(a_i=c_i i!\)，\(b_{n+k-i}=\frac{1}{(i-k)!}\)，原式变成：

\[=n\binom{n}{k}-\frac{1}{k!}\sum_{i=0}^{n+k}a_ib_{n+k-i} \]

后面变成了加法卷积的形式，NTT 即可，时间复杂度 \(O(n \log n)\)。

注意 \(c_0=0\)，算 \(c_i\) 时要特判。

#include<bits/stdc++.h>
#define int long long
#define gc getchar
#define pc putchar
#define rg register
#define LB lower_bound
#define UB upper_bound
#define PII pair<int, int> 
#define PDI pair<double, int>
#define fi first
#define se second
#define IOS ios::sync_with_stdio(0);cin.tie(0);cout.tie(0);
using db=double;using ll=long long;
using ull=unsigned long long;
using namespace std;
const ll INF=1e18;
const int inf=0x3f3f3f3f;
namespace IO{
	inline int read(){
		int x=0,f=1;
		char ch=gc();
		while(!isdigit(ch)){
			if(ch=='-')	f=-f;
			ch=gc();
		}
		while(isdigit(ch)) x=(x<<3)+(x<<1)+ch-'0',ch=gc();
		return x*f;
	}
	inline void write(int x){
		if(x<0) pc('-'),x=-x;
		if(x>9)	write(x/10);
		pc(x%10+'0');
	}
}
using namespace IO;
const int mod=924844033;
const int G=5,Gi=554906420;
const int N=2e5+10,M=6e5+10;
int n,a[M],b[M],sz[N];
int R[M],Lim=1,len;
int fac[N],inv[N];
vector<int> e[N];
inline int qpow(int x, int y){
	int res=1;
	while(y>0){
		if(y&1) res=res*x%mod;
		x=x*x%mod,y>>=1;
	}
	return res;
}
inline void dfs(int u, int fa){
	sz[u]=1;
	for(int v:e[u]) if(v^fa) dfs(v,u),sz[u]+=sz[v];
	if(fa) a[sz[u]]++,a[n-sz[u]]++;
}
inline void NTT(int *a, int flag){
	for(rg int i=0;i<Lim;i++) if(i<R[i]) swap(a[i],a[R[i]]);
	for(rg int h=1;h<Lim;h<<=1){
		int W=qpow((flag==1?G:Gi),(mod-1)/(h<<1))%mod;
		for(rg int j=0;j<Lim;j+=(h<<1)){
			int w=1;
			for(rg int k=j;k<j+h;k++){
				int x=a[k]%mod,y=w*a[k+h]%mod;
				a[k]=(x+y)%mod,a[k+h]=(x-y+mod)%mod;
				w=w*W%mod;
			}
		}
	}
	if(flag==-1){
		int in=qpow(Lim,mod-2)%mod;
		for(rg int i=0;i<Lim;i++) a[i]=a[i]%mod*in%mod;
	}
}
signed main(){
//	freopen("114514.in","r",stdin);
//	freopen("114514.out","w",stdout);
	n=read();
	for(rg int i=1;i<n;i++){
		int u=read(),v=read();
		e[u].push_back(v);
		e[v].push_back(u);
	}
	dfs(1,0);
	fac[0]=1;
	for(rg int i=1;i<=n;i++) fac[i]=fac[i-1]*i%mod;
	inv[n]=qpow(fac[n],mod-2)%mod;
	for(rg int i=n;i>=1;i--) inv[i-1]=inv[i]*i%mod;
	for(rg int i=1;i<=n;i++) a[i]=a[i]*fac[i]%mod;
	for(rg int i=0;i<=n;i++) b[n-i]=inv[i]%mod;
	while(Lim<=2*n) Lim<<=1,len++;
	for(rg int i=0;i<Lim;i++) R[i]=(R[i>>1]>>1)|((i&1)<<(len-1));
	NTT(a,1),NTT(b,1);
	for(rg int i=0;i<Lim;i++) a[i]=a[i]*b[i]%mod;
	NTT(a,-1);
	for(rg int i=1;i<=n;i++){
		int res1=fac[n]%mod*inv[i]%mod*inv[n-i]%mod*n%mod;
		int res2=a[n+i]%mod*inv[i]%mod;
		write((res1-res2+mod)%mod),puts("");
	}
	return 0;
}

T3

求有多少个长度为 \(n\) 的正整数序列 \(a\) 满足：

1.\(\forall i \in [1,n],a_i \in [1,A+B]\)

2.\(\forall a_i \in [1,A]\)，\(a_i\) 的个数为偶数，可以为 \(0\)。

考虑指数型生成函数：

\[f(x)=[1+\frac{1}{2!}x^2+...]^A(1+\frac{1}{1!}x...)^B \]

\[=(\frac{e^x+e^{-x}}{2})^Ae^{Bx} \]

\[=\frac{1}{2^A}\sum_i \binom{A}{i}e^{(A+B-2i)x} \]

\[=\frac{1}{2^A}\sum_i \binom{A}{i}(\sum_j \frac{(A+B-2i)^j}{j!}x^j) \]

于是 \(x^n\) 的系数为 \(\frac{1}{2^A}\sum_i \binom{A}{i}(A+B-2i)^n\)。

T4

原题

10.6

100+100+70+0=270pts，rk4

T1

你遇见了一只玩偶，它的肚子上有一个计数器。

这个计数器的计数上限是 \(m\)，因此当实际值 \(x\) 超过 \(m\) 之后，计数器就只会显示 \(x \bmod m\)。

你需要执行恰好 \(n\) 次操作，每次可以在两种动作中选择一种：轻轻拍它一下，效果为在 \([l_1,r_1]\) 中等概率随机一个整数 \(p\)，使计数器的值增加 \(p\)；狠狠重击，效果为在 \([l_2,r_2]\) 中等概率随机一个整数 \(q\)，使计数器的值增加 \(q\)。

值得注意的是，在每次操作之后，你都可以看到计数器当前的显示值。你的得分被定义为计数器最终的显示值，且你的目标是最大化这一得分。

求在最优策略下的期望得分。

一个期望 dp，设 \(f_{i,j}\) 为还剩 \(i\) 次操作机会，当前分数为 \(j\) 从 \(f_{i-1}\) 转移来的期望分数，边界条件为 \(f_{0,j}=j,j \in [0,m-1]\)。

然后考虑转移，枚举 \(j\)，令：

\[k_1=\frac{1}{r_1-l_1+1}\sum_{p=l_1}^{r_1}f_{i,(j+p) \bmod m} \]

\[k_2=\frac{1}{r_2-l_2+1}\sum_{p=l_2}^{r_2}f_{i,(j+p) \bmod m} \]

有：

\[f_{i,j}=\max\{k_1,k_2\} \]

时间复杂度 \(O(nm^2)\)，期望得分 80pts。注意到每次 \(j\) 加一对于 \(k_1,k_2\) 只有两个端点处的变化，于是可以优化到 \(O(nm)\)。

#include<bits/stdc++.h>
#define int long long
#define gc getchar
#define pc putchar
#define rg register
#define LB lower_bound
#define UB upper_bound
#define PII pair<int, int> 
#define PDI pair<double, int>
#define fi first
#define se second
#define IOS ios::sync_with_stdio(0);cin.tie(0);cout.tie(0);
using db=double;using ll=long long;
using ull=unsigned long long;
using namespace std;
const ll INF=1e18;
const int inf=0x3f3f3f3f;
namespace IO{
	inline int read(){
		int x=0,f=1;
		char ch=gc();
		while(!isdigit(ch)){
			if(ch=='-')	f=-f;
			ch=gc();
		}
		while(isdigit(ch)) x=(x<<3)+(x<<1)+ch-'0',ch=gc();
		return x*f;
	}
	inline void write(int x){
		if(x<0) pc('-'),x=-x;
		if(x>9)	write(x/10);
		pc(x%10+'0');
	}
}
using namespace IO;
const int N=1e5+10;
const int M=1e2+10;
int n,m,l1,l2,r1,r2;
db dp[N][M];
signed main(){
//	freopen("114514.in","r",stdin);
//	freopen("114514.out","w",stdout);
	n=read(),m=read(),l1=read(),r1=read(),l2=read(),r2=read();
	for(int i=0;i<m;i++) dp[0][i]=i;
	for(int i=1;i<=n;i++){
		db k1=0,k2=0;
		for(int k=l1;k<=r1;k++) k1+=dp[i-1][k%m];
		for(int k=l2;k<=r2;k++) k2+=dp[i-1][k%m];
		dp[i][0]=max(k1*1.0/(r1-l1+1),k2*1.0/(r2-l2+1));
		for(int j=1;j<m;j++){
			k1-=dp[i-1][(l1+j-1)%m];
			k1+=dp[i-1][(r1+j)%m];
			k2-=dp[i-1][(l2+j-1)%m];
			k2+=dp[i-1][(r2+j)%m];
			dp[i][j]=max(k1*1.0/(r1-l1+1),k2*1.0/(r2-l2+1));
		}
	}	
	printf("%.2lf",dp[n][0]);
	return 0;
}

T2

9.21 T3 原题。

T3

CF1305F

首先答案一定小于等于奇数个数，否则可以把奇数变成偶数。然后一定有一半及以上的元素加一、减一或不变，于是答案一定是这些元素或操作后元素的因数。

而每个数被加一、减一、不变的概率都大于等于二分之一，于是我们随机选 50 到 60 个数把它们及操作后数质因数分解，这样错误的概率是 \(\frac{1}{2^{50}}\)，可以接受。接着把分解得到的素数全探查一遍，可以给探查的时候加点剪枝，期望时间复杂度 \(O(能过)\)。

T4

原题

10.12

100+30+0+0=130pts

自我反思吧，为什么这么菜。

T1 乱写了个假然后过了，拼劲全力写的 T2T3 挂成一个钢，然后心态爆炸 T4 也没看，痛失 30pts。

T1

原题

T1 放紫是啥？

钦定排序后前一半都组合起来，后一半全单选，枚举断点然后直接做，这样复杂度是 \(O(n^2)\) 的，但是这个是假的，因为存在负数的情况。

考虑避免这种情况，可以发现取单个数相当于取这个数和 \(0\)，于是可以去枚举加入 \(0\) 的个数再排序，这样负数就不会去和负数配对，然后直接对这个序列最小与最大配对，以此类推，复杂度 \(O(n^2 \log n)\)。

#include<bits/stdc++.h>
#define int long long
#define gc getchar
#define pc putchar
#define rg register
#define LB lower_bound
#define UB upper_bound
#define PII pair<int, int> 
#define PDI pair<double, int>
#define fi first
#define se second
#define IOS ios::sync_with_stdio(0);cin.tie(0);cout.tie(0);
using db=double;using ll=long long;
using ull=unsigned long long;
using namespace std;
const ll INF=1e18;
const int inf=0x3f3f3f3f;
namespace IO{
	inline int read(){
		int x=0,f=1;
		char ch=gc();
		while(!isdigit(ch)){
			if(ch=='-')	f=-f;
			ch=gc();
		}
		while(isdigit(ch)) x=(x<<3)+(x<<1)+ch-'0',ch=gc();
		return x*f;
	}
	inline void write(int x){
		if(x<0) pc('-'),x=-x;
		if(x>9)	write(x/10);
		pc(x%10+'0');
	}
}
using namespace IO;
const int N=2e4+10;
int a[N],b[N],n;
signed main(){
//	freopen("114514.in","r",stdin);
//	freopen("114514.out","w",stdout);
	n=read();
	for(rg int i=1;i<=n;i++) b[i]=a[i]=read();
	int ans=INF;
	for(rg int len=n;len<=n*2;len++){
		for(rg int i=n+1;i<=len;i++) a[i]=0;
		sort(a+1,a+1+len);
		int mx=-INF,mi=INF;
		for(rg int i=1;i<=(len>>1);i++){
			mx=max(mx,a[i]+a[len-i+1]);
			mi=min(mi,a[i]+a[len-i+1]);
		}
		if(len&1){
			mx=max(mx,a[len/2+1]);
			mi=min(mi,a[len/2+1]);
		}
		ans=min(ans,mx-mi);
		for(rg int i=1;i<=n;i++) a[i]=b[i];
	}
	write(ans);
	return 0;
}

插排 \(O(n^2)\) 做法。

#include<bits/stdc++.h>
#define int long long
#define gc getchar
#define pc putchar
#define rg register
#define LB lower_bound
#define UB upper_bound
#define PII pair<int, int> 
#define PDI pair<double, int>
#define fi first
#define se second
#define IOS ios::sync_with_stdio(0);cin.tie(0);cout.tie(0);
using db=double;using ll=long long;
using ull=unsigned long long;
using namespace std;
const ll INF=1e18;
const int inf=0x3f3f3f3f;
namespace IO{
	inline int read(){
		int x=0,f=1;
		char ch=gc();
		while(!isdigit(ch)){
			if(ch=='-')	f=-f;
			ch=gc();
		}
		while(isdigit(ch)) x=(x<<3)+(x<<1)+ch-'0',ch=gc();
		return x*f;
	}
	inline void write(int x){
		if(x<0) pc('-'),x=-x;
		if(x>9)	write(x/10);
		pc(x%10+'0');
	}
}
using namespace IO;
const int N=4e4+10;
int a[N],b[N],n;
signed main(){
//	freopen("114514.in","r",stdin);
//	freopen("114514.out","w",stdout);
	n=read();
	for(rg int i=1;i<=n;i++) b[i]=a[i]=read();
	sort(a+1,a+1+n);
	int ans=INF,T=n+1;
	while(T--){
		int mi=inf,mx=-inf;
		for(rg int i=1;i<=(n>>1);i++){
			mi=min(mi,a[i]+a[n-i+1]);
			mx=max(mx,a[i]+a[n-i+1]);
		}
		if(n&1){
			mi=min(mi,a[n/2+1]);
			mx=max(mx,a[n/2+1]);
		}
		ans=min(ans,mx-mi);n++;
		for(rg int i=n;i>1&&a[i-1]>a[i];i--) swap(a[i-1],a[i]);
	}
	write(ans);
	return 0;
}

T2

给定一个字符串 \(S\)，你需要按这种方式生成 \(T\)：

1. \(T_1 = S_1\)。
2. 对于 \(\forall i \in [2,n],T_i = T_{i−1} +S_i +T_{i−1}\)。
   其中 \(+\) 表示拼接。
   求 \(T_n\) 所有子序列中与 \(P\) 相同的个数，答案对 \(998244353\) 取模。

未知原因挂 30pts。

60pts 做法，直接把最终串生成出来 dp，复杂度是 \(O(n2^n)\) 的。

考虑生成操作，每次生成是
\(T_{i-1}+S_i+T_{i-1}\)，如果 \(p[l,mid]\) 和 \(p[mid+1,r]\) 为 \(T_{i-1}\) 的子序列，则这是可以合并的，至于中间的 \(S_i\) 特判一下即可。

于是设 dp 状态 \(f_{i,l,r}\) 为 \(p[l,r]\) 在 \(T_i\) 中的出现次数，转移时枚举转移点 \(mid\)：

\[f_{i,l,r} \leftarrow f_{i,l,r}+f_{i-1,l,mid}*f_{i-1,mid+1,r} \]

每次转移再特判中间的 \(s_i\)，若 \(s_i=p_{mid}\)：

\[f_{i,l,r} \leftarrow f_{i,l,r}+f_{i-1,l,mid-1}*f_{i-1,mid+1,r} \]

复杂度 \(O(n^4)\)，\(100\) 能过。

#include<bits/stdc++.h>
#define int long long
#define gc getchar
#define pc putchar
#define rg register
#define LB lower_bound
#define UB upper_bound
#define PII pair<int, int> 
#define PDI pair<double, int>
#define fi first
#define se second
#define IOS ios::sync_with_stdio(0);cin.tie(0);cout.tie(0);
using db=double;using ll=long long;
using ull=unsigned long long;
using namespace std;
const ll INF=1e18;
const int inf=0x3f3f3f3f;
namespace IO{
	inline int read(){
		int x=0,f=1;
		char ch=gc();
		while(!isdigit(ch)){
			if(ch=='-')	f=-f;
			ch=gc();
		}
		while(isdigit(ch)) x=(x<<3)+(x<<1)+ch-'0',ch=gc();
		return x*f;
	}
	inline void write(int x){
		if(x<0) pc('-'),x=-x;
		if(x>9)	write(x/10);
		pc(x%10+'0');
	}
}
using namespace IO;
const int mod=998244353;
const int N=1e2+10;
char s[N],p[N];
int n,m,f[N][N][N];
signed main(){
//	freopen("114514.in","r",stdin);
//	freopen("114514.out","w",stdout);
	n=read(),m=read();
	scanf("%s",s+1);scanf("%s",p+1);
	for(rg int i=0;i<=n;i++) for(rg int l=1;l<=m+1;l++) f[i][l][l-1]=1;
	for(rg int i=1;i<=n;i++){
		for(rg int l=1;l<=m;l++){
			for(rg int r=l;r<=m;r++){
				for(rg int mid=l-1;mid<=r;mid++){
					f[i][l][r]=(f[i][l][r]+f[i-1][l][mid]*f[i-1][mid+1][r]%mod)%mod;
					if(mid!=l-1&&s[i]==p[mid])
						f[i][l][r]=(f[i][l][r]+f[i-1][l][mid-1]*f[i-1][mid+1][r]%mod)%mod;
				}
			}
		}
	}
	write(f[n][1][m]%mod);
	return 0;
}

T3

给定一个长度为n的数组 \(a_n\)，定义 \(f(s,k)\) 为将所有 \(a_i\) 异或 \(s\)后，\(a_n\)
数组第 \(k\) 小值。
对于每个询问 \((l,r,k)\)，求 \(\sum_{i=l}^r f(i,k)\)。答案对 \(998244353\) 取模。

字典树写炸并非人类。

密码的 60 个 bit 1ll<<bit 不加 ll 是人类吗？警钟撅烂。

首先 \(l=r\) 可以用 01-trie 维护第 k 小，然后 \(n=1\) 可以拆贡献，这样有 20pts。

可惜了，差点写出正解。

首先我们考虑对于一个询问区间 \(([l,r],k)\) 按位拆贡献，设当前位为 \(d\)。有以下两种情况：

• \([l,r]\) 的第 \(d\) 位全部相同，则全都会往一棵子树走。
• \([l,r]\) 的第 \(d\) 位不同，会分裂为两部分往两个子树走。

当前 \(k\) 值大于所相同位子树大小时会产生贡献，而这个是可以 \(O(1)\) 算的，于是我们可以写一个 dfs，但是由于存在分裂的情况，极端数据下复杂度会爆炸。

考虑把询问差分成 \([0,l-1]\) 和 \([0,r]\)，再考虑分裂的情况，注意到每次分裂一定是 \([0,2^d-1]\) 和 \([0.x-2^d]\)，于是我们可以把所有 \([0,2^d-1]\) 深度为 \(d\) 每个节点的每个 \(k\) 值都预处理出来，记为 \(f_{u,k}\)，可以用 vector 存以防止爆炸。这样时间复杂度就做到了 \(O(60(n+q))\)。

不过容易发现差分一下常数乘个 2，容易被卡，于是我们可以把这个过程当成线段树去做，区间取 \([0,2^{60}-1]\)，这样有一个好处就是递归产生的每个区间与 dfs 分裂得到的区间都是相同的，这样就不用差分。

写法上要注意很多细节问题，不然炸成钢，本人菜到调了 2d 最后在 Tyih 巨佬的帮助下调出来了，\bx\bx。

#include<bits/stdc++.h>
#define int long long
#define gc getchar
#define pc putchar
#define rg register
#define LB lower_bound
#define UB upper_bound
#define PII pair<int, int> 
#define PDI pair<double, int>
#define fi first
#define se second
#define IOS ios::sync_with_stdio(0);cin.tie(0);cout.tie(0);
using db=double;using ll=long long;
using ull=unsigned long long;
using namespace std;
const ll INF=1e18;
const int inf=0x3f3f3f3f;
namespace IO{
	inline int read(){
		int x=0,f=1;
		char ch=gc();
		while(!isdigit(ch)){
			if(ch=='-')	f=-f;
			ch=gc();
		}
		while(isdigit(ch)) x=(x<<3)+(x<<1)+ch-'0',ch=gc();
		return x*f;
	}
	inline void write(int x){
		if(x<0) pc('-'),x=-x;
		if(x>9)	write(x/10);
		pc(x%10+'0');
	}
}
using namespace IO;
const int mod=998244353;
const int N=1e5+10;
int n,q,a[N],bit[65],p[65];
vector<int> f[N<<6];
namespace Trie{
	int ch[N<<6][2],cnt=1,sz[N<<6],d[N<<6];
	inline void insert(int x){
		int u=1;sz[u]++;
		for(rg int i=59;i>=0;i--){
			int bit=(x>>i)&1;
			if(!ch[u][bit]) ch[u][bit]=++cnt;
			sz[u=ch[u][bit]]++;
		}
	}
	inline void build(int u, int dep){
		f[u].resize(sz[u]+1);d[u]=dep;
		int ls=ch[u][0],rs=ch[u][1];
		if(!ls&&!rs){
			for(rg int i=1;i<=sz[u];i++) f[u][i]=0;
			return;
		}
		if(ls) build(ls,dep-1);
		if(rs) build(rs,dep-1);
		for(rg int i=1;i<=sz[u];i++){
			int x=0,y=0;
			if(i<=sz[ls]) x=f[ls][i]%mod;
			else x=(f[rs][i-sz[ls]]+bit[dep-1]*bit[dep-1]%mod)%mod;
			if(i<=sz[rs]) y=f[rs][i]%mod;
			else y=(f[ls][i-sz[rs]]+bit[dep-1]*bit[dep-1]%mod)%mod;
			f[u][i]=(x+y)%mod;
		}
	}
	inline int solve(int u, int l, int r, int ql, int qr, int k){
		if(l>=ql&&r<=qr) return f[u][k];
		int mid=l+r>>1,ls=ch[u][0],rs=ch[u][1],ans=0;
		if(ql<=mid){
			if(sz[ls]>=k) ans=(ans+solve(ls,l,mid,ql,qr,k))%mod;
        	else ans=(ans+solve(rs,l,mid,ql,qr,k-sz[ls])+1ll*bit[d[u]-1]*((min(qr,mid)-max(l,ql)+1)%mod))%mod;
		}
		if(qr>mid){
			if(sz[rs]>=k) ans=(ans+solve(rs,mid+1,r,ql,qr,k))%mod;
        	else ans=(ans+solve(ls,mid+1,r,ql,qr,k-sz[rs])+1ll*bit[d[u]-1]*((min(qr,r)-max(mid+1,ql)+1)%mod))%mod;
		}
		return ans%mod;
	}
}using namespace Trie;
signed main(){
//	freopen("114514.in","r",stdin);
//	freopen("114514.out","w",stdout);
	n=read(),q=read();
	for(rg int i=1;i<=n;i++) insert(read());
	bit[0]=p[0]=1;
	for(rg int i=1;i<=61;i++) bit[i]=(bit[i-1]<<1)%mod,p[i]=p[i-1]<<1;
	build(1,60);
	while(q--){
		int l=read(),r=read(),k=read();
		write(solve(1,0,(1ll<<60)-1,l,r,k)%mod);
		puts("");
	}
	return 0;
}

10.19

100+100+0+20=220pts,rk10。

T3 int pushup(int i) 100pts->0pts。

警钟撅烂，写代码一定要开 -Wall。

T1

https://www.luogu.com.cn/article/1ns2c1tf

糖丸了。

T2

原题

考虑设状态 \(f_i\) 为前 \(i\) 个的最小代价，钦定 \(i\) 必选，于是给序列末尾加个 \(0\)。

考虑转移，非常朴素：

\[f_i= \min_j f_j+a_i \]

考虑 \(j\) 的限制条件，首先对于合法的转移，\((j,i)\) 间不能有一个完整的区间，否则这个区间就没法被考虑到，于是设 \(pre_i\) 为能转移到 \(i\) 的最小的 \(j\)，把 \(pre_i\) 预处理出来，然后上面转移是个经典的单调队列，当然想用线段树多个 log 也行。

考虑 \(pre_i\) 的转移，首先 \(pre_1=0\)，每个区间 \([l,r]\) 都有 \(pre_{r+1}=\max\{pre_{r+1},l\}\)，然后其他点有 \(pre_i=\max\{pre_i,pre_{i-1}\}\)。

时间复杂度 \(O(n+q)\)。

T3

原题

考虑设 \(f(l,r)\) 为 \([l,r]\) 的连通块数，考虑固定 \(l\)，从 \(f(l,r)\) 转移到 \(f(l,r+1)\) 时，枚举 \(r+1\) 相连的点 \(v\)，设 \(v \in [l,r]\) 的 \(v\) 有 \(num\) 个，那么有 \(f(l,r+1)=f(l,r)-(num-1)\)。

这是因为所有与 \(r+1\) 相连的 \(v\) 都各自在一个单独的连通块内，假设两个点处于相同连通块，它们又与 \(r+1\) 相连，那么存在两条路径可以互达，与树矛盾。

于是我们可以枚举 \(r\)，每次给 \(l \in [1,r]\) 的 \(f(l,r)\) 加一，给 \(\forall v \rightarrow r,l \in [1,v]\) 的 \(f(l,r)\) 减一，对每个 \(r\) 统计 \(l \in [1,r]\) 的 \(f(l,r)=1\) 的个数。这个东西显然是一个区间加区间 min 线段树板子，注意 pushup 要 void！

T4

给定两棵节点数为 \(n\) 的树 \(A,B\)，树上有边权。每次询问给定 \(a,b\)，求 \(\max_{i=1}^n dis_A(a,i)+dis_B(b,i)\)。

暴力有 40pts，可惜因为没写 RMQLCA 挂了 20pts，wssb。

10.22

100+100+40+0=240pts

T1

给定两张 \(n\) 个点的简单无向图 \(G_1,G_2\)。

每次可以交换两个点的编号，这样它们对应的边也会随之改变，求至少需要多少次操作才能将 \(G_1\) 变成 \(G_2\)。

定义两张图相同，当且仅当对于每条边在两张图中的存在性相同。

交换显然可以看成轮换，可以考虑爆搜，枚举全排列即可。

#include<bits/stdc++.h>
using namespace std;
using ll=long long;
const int N=11,INF=1e9;
int n,p[N],vis[N];
char a[N][N],b[N][N];
bool chk(){
	for(int i=1;i<=n;i++)for(int j=1;j<=n;j++){
		if(a[p[i]][p[j]]!=b[i][j])return 0;
	}
	return 1;
}
int main(){
	scanf("%d",&n);
	for(int i=1;i<=n;i++)scanf("%s",a[i]+1);
	for(int i=1;i<=n;i++)scanf("%s",b[i]+1);
	iota(p,p+1+n,0);
	int ans=INF;
	do{
		if(!chk())continue;
		int cnt=n;
		fill(vis,vis+1+n,0);
		for(int i=1;i<=n;i++)if(!vis[i]){
			for(int x=i;!vis[x];x=p[x])vis[x]=1;
			cnt--;
		}
		ans=min(ans,cnt);
	}while(next_permutation(p+1,p+1+n));
	cout<<ans;
	return 0;
}

T2

给定一个长度为 \(n\) 的序列。你可以将它划分成任意个非空连续段，但要求第 \(i\) 段中所有元素的 \(i\) 次方和是 \(i\) 的倍数。求方案数在模 \(998244353\) 意义下的值。

一个很典的 dp。

显然可以先预处理出每个前缀的 \(k\) 次和模 \(k\)，对于一个 \(k\)，有两个前缀模 \(k\) 相同，那么他们形成的区间可以做第 \(k\) 段。

设 \(f_{i,j}\) 为前 \(i\) 个数分成 \(j\) 段的方案数，有：

\[f_{i,j}= \sum_{k 符合条件} f_{k,j-1} \]

然后前缀和优化一下，转移的复杂度是 \(O(n^2)\) 的。

const int mod=998244353;
const int N=2e3+10;
int n,a[N],p[N][N],f[N][N],g[N][N];
inline int qpow(int x, int y, int p){
	int ans=1;
	while(y>0){
		if(y&1) ans=ans*x%p;
		x=x*x%p,y>>=1;
	}
	return ans%p;
}
signed main(){
//	freopen("114514.in","r",stdin);
//	freopen("114514.out","w",stdout);
	n=read();
	for(rg int i=1;i<=n;i++){
		a[i]=read();
		for(rg int j=1;j<=i;j++) 
			p[i][j]=(p[i-1][j]+qpow(a[i]%j,j,j))%j;
	}
	g[0][0]=1;
 	for(rg int j=1;j<=n;j++){
 		for(rg int i=1;i<=n;i++){
 			(f[i][j]+=g[p[i][j]%j][j-1])%=mod;
 			(g[p[i][j]%j][j-1]+=f[i][j-1])%=mod;
		}
	}
	int ans=0;
	for(rg int k=1;k<=n;k++) ans=(ans+f[n][k])%mod;
	write(ans);
	return 0;
}

T3

给定一张 \(n\) 个点 \(m\) 条边的无向图，你的任务是为每条边定向，将它变成一个有向图。
求定向后存在 \(a\) 使得从 \(1\) 号点和 \(2\) 号点出发都能够到达 \(a\) 号点的方案数。（特别地，\(a\) 可以是 \(1\) 或 \(2\)）

你只需求出答案在模 \(998244353\) 意义下的值。

很明显这是个状压 dp，考虑让这玩意变成 0-index。

考虑容斥，转换为不存在 \(a\) 使得 \(0,1\) 都能到达 \(a\) 的方案数，设 \(0\) 能到达的点集为 \(S\)，\(1\) 为 \(T\)，使得上述条件不成立，必须让 \(S\) 与 \(T\) 无连边，这样整个图会被分成 \(3\) 个集合， \(S,T\) 与中间部分 \(U \backslash S \backslash T\)。

于是答案会变成：

\[2^m-\sum_{0 \in S \subseteq U} \sum_{1 \in T \subseteq U} [S \cap T = \varnothing] [E(S \cup T)=E(S)+E(T)]f(S)g(T)2^{E(U \backslash S \backslash T)} \]

其中 \(f,g\) 表示包含 \(0/1\) 节点的集合内的连边方案，为什么不能乱连呢，因为要保证 \(0/1\) 可以到达集合内任意一个点。

\(E(S)\) 表示 \(S\) 集合内点的边数。

首先考虑这个 \(E\) 怎么转移，边界条件显然是：

\[E(\{u,v\})=1,(u \rightarrow v) \]

然后显然有一个很朴素的转移，倒着转移，有：

\[E(S)=\sum_{T \subset S} E(T) \]

这个复杂度 \(O(3^n)\)。

然后考虑 \(f,g\) 的转移，你会发现这两个转移是一样的，都用 \(f\) 代替，包含的起点设为 \(p\)，考虑容斥，显然如果不满足条件，则包含 \(p\) 的一个子集 \(T\) 没有向外连边，方案数为 \(f(T)\)，然后另外一部分 \(S \backslash T\) 可以随便连。

\[f(S)=2^{E(S)}-\sum_{p \in T \subset S}f(T)2^{E(S \backslash T)} \]

然后你就做完了，复杂度 \(O(3^n)\)。

const int N=20;
const int M=150;
const int mod=998244353;
int n,m,p[M],E[1<<N],f[1<<N],g[1<<N];
signed main(){
//	freopen("114514.in","r",stdin);
//	freopen("114514.out","w",stdout);
	n=read(),m=read();
	p[0]=1;
	for(rg int i=1;i<=m;i++){
		int u=read()-1,v=read()-1;
		E[(1<<u)|(1<<v)]=1,p[i]=(p[i-1]<<1)%mod;
	}
	int U=(1<<n)-1;
	for(rg int S=U;S;S--) for(rg int T=S&(S-1);T;T=(T-1)&S) E[S]+=E[T];
	if(E[3]) return write(p[m]%mod),0;
	f[1]=1;
	for(rg int S=5;S<=U;S+=4){
		if(!(S&1)) continue;
		for(rg int T=S&(S-1);T;T=(T-1)&S)  if(T&1) f[S]=(f[S]+f[T]*p[E[S^T]]%mod)%mod;
		f[S]=(p[E[S]]-f[S]+mod)%mod;
	}
	g[2]=1;
	for(rg int S=6;S<=U;S+=4){
		if(!(S&2)) continue;
		for(rg int T=S&(S-1);T;T=(T-1)&S)  if(T&2) g[S]=(g[S]+g[T]*p[E[S^T]]%mod)%mod;
		g[S]=(p[E[S]]-g[S]+mod)%mod;
	}
	int ans=0;
	for(rg int S=1;S<=U;S+=2){
		int P=U^S;
		for(rg int T=P;T;T=(T-1)&P){
			if(!(T&2)) continue;
			if(E[S|T]!=E[S]+E[T]) continue;
			ans=(ans+f[S]*g[T]%mod*p[E[U^S^T]]%mod)%mod;
		}
	}
	write((p[m]-ans+mod)%mod);
	return 0;
}

T4

某年 IOI 题，不会。

10.24

差点 AK。

T1

给定一个自然数 \(N\)，找出一个 \(M\)，使得 \(M > 0\) 且 \(M\) 是 \(N\) 的倍数，并且 \(M\) 的十进制表示只包含\(0\) 或 \(1\)。求最小的 \(M\)。如果无解，则输出 \(-1\)。

显然你可以打个广搜，直接输出路径即可，你会发现无解是不可能的，然后注意特判 \(n=1\)。

T2

定义两个 01 串的相似值为：如果两个串在第 \(i\) 位是一样的，那么他们的相似值要加上 \(w_i\)。

现在给你 \(m\) 个长度为 \(n\) 的 01 串，然后有 \(q\) 个询问，每一次给定一个长度为 \(n\) 的 01 串和一个值 \(k\) 求在这 \(m\) 个串中，有多少个串和他的相似值不超过 \(k\)。

怎么放 \(O(4^n)\) 暴力过了？

SOSdp 好题。

可转化为：把第 \(i\) 位取反的代价为 \(w_i\)，求在 \(k\) 的代价以内可以把串变成与文本串完全不同的文本串数量。

设 \(f_{i,S,k}\) 表示只考虑前 \(i\) 位把 \(S\) 变成与文本串不同的代价不超过 \(k\) 的文本串数量。

当 \(w_i>k\)，有 \(f_{i,S,k}=f_{i-1,S,k}\)；当 \(w_i \leq k\)，有 \(f_{i,S,k}=f_{i-1,S,k}+f_{i-1,S \backslash \{i\},k-w_i}\)，复杂度 \(O(2^nnk)\)。

T3

给出 \(t\) 个数字，其中包括一个 \(0\)，求是否存在一个 \(n \times m=t\) 的矩阵，在其中选定一个特殊格子 \((x,y)\)，然后把 \(t\) 个数字填到这个矩阵中，满足每个格子上的数字就是到特殊格子的曼哈顿距离。如果有多种方案，输出任意一种即可。如果无解，输出 \(-1\)。

你会发现满足距离相同的点是一圈菱形，它们的个数是距离的 \(4\) 倍，如果个数不足这个值，说明它被边界顶掉了，这样我们直接把 \(x\) 找出来了。

然后枚举 \(n,m\)，你会发现 \((n,m)\) 到 \((x,y)\) 的距离是序列 max，设为 \(b\)，于是 \(y=n+m-x-b\)，然后你就可以判断是否成立了。

const int N=1e6+10;
int t,cnt[N],a,b,m,n;
int p[N];
signed main(){
//	freopen("114514.in","r",stdin);
//	freopen("114514.out","w",stdout);
	t=read();
	for(rg int i=1;i<=t;i++){
		int x=read();
		cnt[x]++,b=max(b,x);
	}
	int x=0,y=0;
	for(rg int i=1;i<=t;i++){
		if(cnt[i]<i*4){
			x=i;
			break;
		}
	}
	for(rg int i=1;i<=t;i++){
		if(t%i) continue;
		n=i,m=t/i,y=n+m-x-b;
		memset(p,0,sizeof p);
		if(abs(n-x)+abs(m-y)==b){
			for(rg int j=1;j<=n;j++)
				for(rg int k=1;k<=m;k++)
					p[abs(j-x)+abs(k-y)]++;
			bool flag=1;
			for(rg int i=0;i<=b;i++) 
				if(cnt[i]!=p[i]){
					flag=0;
					break;
				}
			if(flag==1){
				write(n),pc(' '),write(m),puts("");
				write(x),pc(' '),write(y),puts("");
				return 0;
			}
		}
	}
	puts("-1");
	return 0;
}

T4

原题

依旧 SOSdp，你可以把 \(a_i\) 取反，求 \(a_j \subseteq a_i\)，然后很唐。

const int N=1e6+10;
const int M=22;
const int U=(1<<M)-1;
int n,a[N],f[1<<M];
signed main(){
//	freopen("114514.in","r",stdin);
//	freopen("114514.out","w",stdout);
	memset(f,-1,sizeof f);
	n=read();
	for(rg int i=1;i<=n;i++) a[i]=read(),f[a[i]]=a[i];
	for(rg int S=0;S<=U;S++){
		if(f[S]!=-1) continue;
		for(rg int i=0;i<22;i++){
			if(S&(1<<i)){
				if(f[S^(1<<i)]!=-1){
					f[S]=f[S^(1<<i)];
					break;
				}
			}
		}
	}
	for(rg int i=1;i<=n;i++) write((~f[U&(~a[i])])?1:0),pc(' ');
	return 0;
}

10.25

T1

给 \(n\) 个点，每个点 \(i\) 有 \(a_i,b_i\)，表示 \(i\) 向 \([a_i,i]\) 连 \(1\) 的边，\([i,b_i]\) 向 \(i\) 连 \(1\) 的边，求任意两点的最短路。

考虑一个起点 \(s\)。

对于 \(i>s\) 肯定是一直往右跳到某个 \(j\)，然后往左跳或者不跳，到 \(i\)。

对于 \(i<s\)，要么一直往左，要么按 \(j>s\) 的最优方案跳到一个 \(j\) 再一直往左。

dp 一下即可。

inline void solve(int s){
	fill(f+1,f+1+n,inf),f[s]=0;
	fill(pos+1,pos+1+n,n+1),pos[0]=s;
	for(rg int x=0,i=s+1;i<=n;i++){
		x++;
		while(x>0&&pos[x-1]>=b[i]) x--;
		pos[f[i]=x+1]=i;
	}
	fill(pos,pos+1+n,n+1);
	for(rg int i=n,x=inf;i>=1;i--){
		x=min(x+1,f[i]);
		while(x>0&&pos[x-1]<=i) x--;
		f[i]=min(f[i],x+1);
		pos[f[i]]=min(pos[f[i]],a[i]);
	}
	for(rg int i=1;i<=n;i++) ans^=f[i]*(i+s);
}

T2

有⼀棵 \(n\) 个节点的树，每条边⻓度为 \(1\)，颜⾊为⿊或⽩。 可以执⾏若⼲次如下操作：选择⼀条简单路径，反转路径上所有边的颜⾊。对于某些边，要求在操作结束时为某⼀种颜⾊。给定每条边的初始颜⾊，求最⼩操作数，以及满⾜操作数最⼩时，最⼩的操作路径⻓度和。

可通过将目标颜色和当前颜色的转化，将问题转化为：给定若干个点的颜色，其余点的颜色可以任意取，求答案。

树形 dp，设 \(f_{i,0/1}\) 表示 \(i\) 到它父亲的这条边为 \(0/1\) 这种颜色的最优答案。

可以将与 \(i\) 这个点连的边合并成一条路径，两个单独的路径合并可以使操作次数减 \(1\)。分别考虑奇数条边与偶数条边的转移即可。

#define mp make_pair 
const int N=1e5+10;
int n;
PII f[N][2];
vector<PII> e[N];
PII operator + (PII a, PII b){
	return mp(a.fi+b.fi,a.se+b.se);
}
inline void dfs(int u, int fa, int op){
	PII p1={inf,inf},p2={0,0};
	for(auto p:e[u]){
		int v=p.fi,o=p.se;
		if(v==fa) continue;
		dfs(v,u,o);
		PII l1=p1,l2=p2;
		p1=min(l1+f[v][0],l2+f[v][1]);
		p2=min(l2+f[v][0],l1+f[v][1]);
	}
	if(op==1||op==2) f[u][1]=min(mp(p1.fi,p1.se+1),mp(p2.fi+1,p2.se+1));
	else f[u][1]=mp(inf,inf);
	//
	if(op==0||op==2) f[u][0]=min(p2,mp(p1.fi+1,p1.se));
	else f[u][0]=mp(inf,inf);
}
signed main(){
//	freopen("114514.in","r",stdin);
//	freopen("114514.out","w",stdout);
	n=read();
	for(rg int i=1;i<n;i++){
		int u=read(),v=read(),c=read(),d=read();
		int op=(d==2)?2:((c^d)?1:0);
		e[u].emplace_back(v,op);
		e[v].emplace_back(u,op);
	}
	dfs(1,0,2);
	write(f[1][0].fi/2),pc(' '),write(f[1][0].se);
	return 0;
}

T3

初始时，在数轴上有⼀个线段，左端点在 \(0\)，⻓度为 \(l\)。
现在需要按顺序完成 \(n\) 个任务，第 \(i\) 个任务可以⽤ \(x_i\) 表示:当线段接触到点 \(x_i\) 时，视为完成任务，你可以任意平移线段，求依次完成任务所需要的最短的平移总距离。\(q\) 次询问，每次给出⼀个 \(l\)。

不会。

T4

给定一个序列 \(a\)，\(q\) 个操作，有两种，把一个点修改为 \(k\)，或者求区间 \([l,r]\) 选三个元素作为三角形边长，求三角形边长 max 或者报告不能组成三角形。

注意到最坏情况就是斐波那契数列，任意三项都不能组成三角形，但是这个东西增长很快，前 \(50\) 项就会超过 \(10^9\)，所以直接线段树维护区间前 \(50\) 大即可。

const int N=1e5+10;
int n,q,a[N];
namespace SGT{
	int tr[N<<2][65],cnt[N<<2];
	inline void pushup(int i){
		cnt[i]=0;int L=1,R=1;
		while(cnt[i]<=50){
			int l=(L<=cnt[i<<1])?tr[i<<1][L]:0;
			int r=(R<=cnt[i<<1|1])?tr[i<<1|1][R]:0;
			if(l==0&&r==0) break;
			if(l>r) tr[i][++cnt[i]]=l,L++;
			else tr[i][++cnt[i]]=r,R++;
		}
	}
	inline void build(int i, int l, int r){
		if(l==r){
			tr[i][1]=a[l],cnt[i]=1;
			return;
		}
		int mid=l+r>>1;
		build(i<<1,l,mid);
		build(i<<1|1,mid+1,r);
		pushup(i);
	}
	inline void modify(int i, int l, int r, int k, int d){
		if(l==r){
			tr[i][1]=d,cnt[i]=1;
			return;
		}
		int mid=l+r>>1;
		if(k<=mid) modify(i<<1,l,mid,k,d);
		else modify(i<<1|1,mid+1,r,k,d);
		pushup(i);
	}
	int ans[65],res[65],num;
	void merge(int i){
		memset(res,0,sizeof res);
		int L=1,R=1,tot=0;
		while(tot<=50){
			int l=(L<=cnt[i])?tr[i][L]:0;
			int r=(R<=num)?ans[R]:0;
			if(l>r) res[++tot]=l,L++;
			else res[++tot]=r,R++;
		}
		memcpy(ans,res,sizeof res);
		num=tot;
	}
	inline void query(int i, int l, int r, int ql, int qr){
		if(ql<=l&&qr>=r){
			merge(i);
			return;
		}
		int mid=l+r>>1;
		if(ql<=mid) query(i<<1,l,mid,ql,qr);
		if(qr>mid) query(i<<1|1,mid+1,r,ql,qr);
	}
	inline int solve(int l, int r){
		memset(ans,0,sizeof ans);num=0;
		query(1,1,n,l,r);
		if(num<3) return 0;
		for(rg int i=1;i+2<=num;i++)
			if(ans[i+1]+ans[i+2]>ans[i])
				return ans[i+1]+ans[i+2]+ans[i];
		return 0;
	}
}using namespace SGT;

10.26

T1

原题

神秘结论题。

你会发现如果有个 \(B\) 在一个 \(A\) 前面或者没有 \(B\) 答案就一定是 \(A\)，否则是 \(B\)，感性理解一下即可。

T2

原题

不会。

T3

密码的这不暑假原题吗？

给出了一个 \(N\) 个点 \(M\) 条边的有向图。求有多少个有序点对 \((a,b)\)，满足至少存在一个点 \(c\) 以及从 \(c\) 到 \(a\) 的一条路径 \(L_a\)，\(c\) 到 \(b\) 的一条路径 \(L_b\)，使得 \(L_a\) 的长度是 \(L_b\) 的两倍（长度指的经过的边的数目）（\(|L_a|,|L_b|\ge 0\)）。注意不一定是简单路径。

考虑 dp，设 \(f_{i,j}=1/0\) 为点对 \((i,j)\) 是否符合条件，初始 \(f_{i,i}=1\)，对于每个 \(i\) 可以沿边搜索，先对 \(i\) 走两步，再对 \(j\) 走一步，得到的两个点记录答案。

但我们还需记录状态，可以给 f 再加一维 \(f_{i,j,0/1/2}\) 表示状态对 \(j\) 走一步或初始状态、对 \(i\) 走一步、对 \(i\) 走两步，具体的状态转移如下：

\[(u,v,0) \rightarrow (u_1,v,1) \rightarrow (u_2,v,1) \rightarrow (u_2,v_1,0) \]

写个 bfs 扩展即可，时间复杂度为 \(O(nm)\)。

T4

原题

不会。

10.27

T1

Galen 花重金收购了一个停车场。共有一排车位，编号为 \(1 ∼ N\)。Galen 不希望自己的停车场看起来过于拥挤，因此，Galen 会给每个来停车的客户指定车位。

指定车位的规则是：

选择间隔最大的两辆车 (你可以认为 \(0\) 和 \(N + 1\) 也算一辆车，如果有多个间隔，则选择最靠左的)，然后把车停在两辆车的中间（如果两辆车中间的车位恰好是奇数，则停在正中间，否则停在正中间的左边车位）。

不巧的是，这些车主都是不好打搅的主，他们各自有一个心理底线 \(a_i\)，一旦有一辆车（不包括 \(0\) 和 \(N + 1\)）跟他的距离小于等于 \(a_i\) 时，他就会无法忍受，直接开车离去。同理，如果他被分配的车位一开始就不满足要求，他就不会在这个停车场停车。

Galen 希望在开业的第一天，所有客户都能在这停车，于是决定用钱收买他们。确切的说，Galen 每花 \(1\) 元，可以让一个客户的 \(a_i\) 减 \(1\)。现在的问题是，Galen 最少要花多少钱，才能使得所有客户都在他的停车场停车。

唐无边的贪心题，直接写个优先队列做一下就好了。

const int N=1e6+10;
struct node{
	int pos,w;
}a[N];
bool cmp(node x, node y){return x.pos<y.pos;}
struct seg{
	int l,r,len;
	bool operator < (const seg &A)const{
		if(A.len!=len) return A.len>len;
		return A.l<l;
	}
};
priority_queue<seg> q;
int n,m;
signed main(){
//	freopen("114514.in","r",stdin);
//	freopen("114514.out","w",stdout);
	n=read(),m=read();
	for(rg int i=1;i<=m;i++) a[i].w=read();
	q.push({1,n,n});
	for(rg int i=1;i<=m;i++){
		auto p=q.top();q.pop();
		int mid=(p.l+p.r)>>1;
		a[i].pos=mid;
		if(p.l<=mid-1) q.push({p.l,mid-1,mid-p.l});
		if(p.r>=mid+1) q.push({mid+1,p.r,p.r-mid});
	}
	sort(a+1,a+1+m,cmp);
	int ans=0;
	for(rg int i=1;i<=m;i++){
		if(i==1){
			int dis=a[i+1].pos-a[i].pos,w=a[i].w;
			ans+=(dis>w?0:w-dis+1);
		}else if(i==m){
			int dis=a[i].pos-a[i-1].pos,w=a[i].w;
			ans+=(dis>w?0:w-dis+1);
		}else{
			int d1=a[i].pos-a[i-1].pos,d2=a[i+1].pos-a[i].pos,w=a[i].w;
			int dis=min(d1,d2);
			ans+=(dis>w?0:w-dis+1);
		}
	}
	write(ans);
	return 0;
}

T2

打怪兽，地图上有 \(n\) 个点，构成一棵树形结构。
初始你在 \(1\) 号点，对于 \(2 ∼ n\) 中的每个点，上面都恰有一只怪兽。每只怪兽都可以用一个二元组 \((a_i,b_i)\) 表示。当你第一次碰到它时，它会与你开战，先对你造成 \(a_i\) 点伤害，战斗结束后你可以恢复 \(b_i\) 点血量。此后再次经过它所在节点不会产生任何影响。

你可以在地图上移动并决策打怪兽的顺序，但如果某一时刻你的血量变成负数，那么你就输了。求取得最终胜利，初始血量的最小值。

又是一个贪心，首先对于 \(b_i>a_i\) 的，肯定打 \(a_i\) 小的。然后再打 \(b_i<a_i\) 的，在这里面要先打 \(b_i\) 大的，因为你总共扣的血都是一样的，那肯定
加回来的越多越好。

于是考虑把所有怪加到优先队列里，但是还有个树的限制，于是考虑把怪物和它父节点合并，对于两个怪 \((a_1,b_1),(a_2,b_2)\)，若 \(b_1>a_2\)，变为 \((a_1,b_1-a_2+b_2)\)，反之变为 \((a_1-b_1+a_2,b_2)\)。

按顺序合并到最后剩一个节点即可。

const int N=1e5+10;
struct node{
	int a,b,id;
	bool operator <(const node& x)const{
		if(a>=b&&x.a<x.b) return 1;
		if(a<b&&x.a>=x.b) return 0;
		if(a>=b&&x.a>=x.b) return b<x.b;
		if(a<b&&x.a<x.b) return a>x.a;
	}
	void operator +=(const node &x){
		int A=max(a,a-b+x.a);
		int B=b-a+x.b-x.a+A;
		a=A,b=B;
	}
}p[N];
priority_queue<node> q;
vector<int> e[N];
int n,f[N];
inline void dfs(int u, int fa){f[u]=fa;for(int v:e[u]) if(v^fa) dfs(v,u);}
int fa[N];
bool vis[N];
inline int find(int x){return (fa[x]==x)?fa[x]:fa[x]=find(fa[x]);}
signed main(){
//	freopen("114514.in","r",stdin);
//	freopen("114514.out","w",stdout);
	n=read();
	for(rg int i=2;i<=n;i++){
		p[i].a=read(),p[i].b=read(),p[i].id=i;
		q.push(p[i]);
	}
	p[1]={0,0,1};
	for(rg int i=1;i<n;i++){
		int u=read(),v=read();
		e[u].push_back(v);
		e[v].push_back(u);
	}
	dfs(1,0);iota(fa+1,fa+1+n,1);
	while(!q.empty()){
		node u=q.top();q.pop();
		if(vis[u.id]) continue;
		vis[u.id]=1;int Fa=find(f[u.id]);fa[u.id]=Fa;
		p[Fa]+=p[u.id];
		if(Fa^1) q.push(p[Fa]);
	}
	write(p[1].a);
	return 0;
}

T3

原题

首先考虑全局异或 max 的两个点 \((x,y)\)，那么不在 \(x \rightarrow 1\) 和 \(y \rightarrow 1\) 两条链上的点的答案都是全局 max，这个显然是 01-trie 板子，复杂度 \(O(60n)\)。

然后考虑这两条链，你会发现其实可以从根开始往下加点，在这个过程中求答案，这玩意的复杂度还是 \(O(60n)\)。

然后就做完了，但并不是很好写。

T4

不会。

10.28

T1

给你一棵 \(n\) 个节点的树, 每次询问包含第 \(i\) 条边的树上最长路径长度。

换根 dp，非常唐，但是注意特判不然挂很惨。

const int N=1e6+10;
int n,dis[N],cnt,son[N];
int pre[N],suf[N],f[N],p[N];
vector<int> to[N];
PII e[N];
inline void dfs(int u, int fa){
	p[u]=fa;
	for(int v:to[u]){
		if(v==fa) continue;
		dfs(v,u);dis[u]=max(dis[u],dis[v]+1);
	}
}
inline void dp(int u, int fa){
	cnt=0;
	for(int v:to[u]) if(v^fa) son[++cnt]=v;
	pre[0]=suf[cnt+1]=0;
	for(rg int i=1;i<=cnt;i++) pre[i]=max(pre[i-1],dis[son[i]]);
	for(rg int i=cnt;i>=1;i--) suf[i]=max(suf[i+1],dis[son[i]]);
	for(rg int i=1;i<=cnt;i++) f[son[i]]=max({f[u],pre[i-1],suf[i+1]})+1;
	if(u==1&&cnt==1) f[to[u][0]]=0;
	for(int v:to[u]) if(v^fa) dp(v,u);
}
signed main(){
//	freopen("114514.in","r",stdin);
//	freopen("114514.out","w",stdout);
	n=read();
	for(rg int i=1;i<n;i++){
		int u=read(),v=read();e[i]={u,v};
		to[u].emplace_back(v);
		to[v].emplace_back(u);
	}
	dfs(1,0);
//	for(rg int i=1;i<=n;i++) write(dis[i]),pc(' ');
	dp(1,0);
	for(rg int i=1;i<n;i++){
		int u=e[i].fi,v=e[i].se;
		if(p[u]==v) swap(u,v);
		write(f[v]+dis[v]+1);puts("");
	}
	return 0;
}

T2

给出一个 \(n\) 个点，\(m\) 条边的无向图。接下来 \(Q\) 次询问，每次从图中删掉一个点 \(A\) 后，请问此时点 \(B\) 到点 \(C\) 的最短路长度，询问独立。

Floyd 支持 \(O(n^3)\) 加入一个点，把询问全存下来离线分治即可，复杂度 \(O(n^3 \log n)\)。

const int N=205;
const int M=1e5+10;
struct qry{
	int id,s,t;
};vector<qry> q[N];
int n,m,Q,ans[M];
int a[N][N],g[25][N][N];
inline void solve(int l, int r, int d){
	if(l==r){
		for(auto p:q[l]) ans[p.id]=g[d-1][p.s][p.t];
		return;
	}
	int mid=l+r>>1;
	for(rg int i=1;i<=n;i++) for(rg int j=1;j<=n;j++) g[d][i][j]=g[d-1][i][j];
	for(rg int k=mid+1;k<=r;k++){
		for(rg int i=1;i<=n;i++){
			for(rg int j=1;j<=n;j++)
				g[d][i][j]=min(g[d][i][j],g[d][i][k]+g[d][k][j]);
		}
	}
	solve(l,mid,d+1);
	for(rg int i=1;i<=n;i++) for(rg int j=1;j<=n;j++) g[d][i][j]=g[d-1][i][j];
	for(rg int k=l;k<=mid;k++){
		for(rg int i=1;i<=n;i++){
			for(rg int j=1;j<=n;j++)
				g[d][i][j]=min(g[d][i][j],g[d][i][k]+g[d][k][j]);
		}
	}
	solve(mid+1,r,d+1);
}
signed main(){
//	freopen("114514.in","r",stdin);
//	freopen("114514.out","w",stdout);
	n=read(),m=read(),Q=read();
	for(rg int i=1;i<=n;i++)
		for(rg int j=1;j<=n;j++)
			a[i][j]=INF;
	for(rg int i=1;i<=m;i++){
		int u=read(),v=read(),w=read();
		a[u][v]=a[v][u]=min(a[u][v],w);
	}
	for(rg int i=1;i<=n;i++) for(rg int j=1;j<=n;j++) g[0][i][j]=a[i][j];
	for(rg int i=1;i<=Q;i++){
		int u=read(),s=read(),t=read();
		q[u].push_back({i,s,t});
	}
	solve(1,n,1);
	for(rg int i=1;i<=Q;i++) write((ans[i]==INF)?-1:ans[i]),puts("");
	return 0;
}

T3

有 \(n\) 个点，位置为 \(p_i\)，权值为 \(a_i\)，维护两种操作，一个是区间加，一个是区间循环移位。

每次询问求使 \(\sum_{i=1}^{n} a_i \times |p_i-P|\) 最小的一个位置 \(P\) 值。

首先区间循环移位可以看成两个区间翻转，然后加上区间加其实就是个文艺平衡树。

不难发现这个 \(P\) 其实就是使得 \(\sum_{i=1}^x a_x > \lfloor \frac{s+1}{2}\rfloor\) 的最小 \(x\) 对应的位置 \(p_x\)，只需平衡树上二分一下即可。

const int N=1e5+10;
int n,m,p[N];
namespace FHQ{
	#define ls(i) tree[i][0]
	#define rs(i) tree[i][1]
	int root,tot,tree[N][2],size[N];
	int val[N],pri[N],lazy[N],add[N],sum[N];
	inline int newnode(int x){
		int u=++tot;
		pri[u]=rand(),val[u]=sum[u]=x,size[u]=1;
		ls(u)=rs(u)=0;
		return u;
	}
	inline void pushup(int u){
		size[u]=size[ls(u)]+size[rs(u)]+1;
		sum[u]=sum[ls(u)]+sum[rs(u)]+val[u];
	}
	inline void pushdown(int i){
		if(lazy[i]){
			if(ls(i)) lazy[ls(i)]^=1;
			if(rs(i)) lazy[rs(i)]^=1;
			swap(ls(i),rs(i));
			lazy[i]=0;
		}
		if(add[i]){
			if(ls(i)) add[ls(i)]+=add[i],val[ls(i)]+=add[i],sum[ls(i)]+=size[ls(i)]*add[i];
			if(rs(i)) add[rs(i)]+=add[i],val[rs(i)]+=add[i],sum[rs(i)]+=size[rs(i)]*add[i];
			add[i]=0;
		}
	}
	inline void split(int u, int k, int &L, int &R){
		if(!u) return L=R=0,void();
		pushdown(u);
		if(size[ls(u)]+1<=k) L=u,split(rs(u),k-size[ls(u)]-1,rs(u),R);
		else R=u,split(ls(u),k,L,ls(u));
		pushup(u);
	}
	inline int merge(int L, int R){
		if(!L||!R) return L|R;
		pushdown(L),pushdown(R);int u;
		if(pri[L]<pri[R]) rs(L)=merge(rs(L),R),u=L;
		else ls(R)=merge(L,ls(R)),u=R;
		pushup(u);
		return u;
	}
	inline void insert(int x){
		int u=newnode(x);
		root=merge(root,u);
	}
	inline void modify(int l, int r, int d){
		int L,R,p;
		split(root,r,L,R);
		split(L,l-1,L,p);
		add[p]+=d,val[p]+=d,sum[p]+=d*size[p];
		root=merge(merge(L,p),R);
	}
	inline void reverse(int l, int r){
		int L,R,p;
		split(root,r,L,R);
		split(L,l-1,L,p);
		lazy[p]^=1;
		root=merge(merge(L,p),R);
	}
	inline int query(int w){
		int u=root,ans=0;
		while(u){
			pushdown(u);
			if(ls(u)&&w<=sum[ls(u)]) u=ls(u);
			else{
				int tmp=(ls(u)?sum[ls(u)]:0)+val[u];
				ans+=(ls(u)?size[ls(u)]:0)+1;
				if(tmp>=w) return ans;
				w-=tmp,u=rs(u);
			}
		}
	}
}using namespace FHQ;
signed main(){
//	freopen("114514.in","r",stdin);
//	freopen("114514.out","w",stdout);
	srand(Ruby);
	n=read(),m=read();
	int s=0;
	for(rg int i=1;i<=n;i++){
		int x=read();insert(x);
		s+=x;
	}
	for(rg int i=1;i<=n;i++) p[i]=read();
	int res=query((s+1)/2);
	write(p[res]);puts("");
	while(m--){
		char op;scanf("%c ",&op);
		if(op=='A'){
			int l=read(),r=read(),d=read();
			s+=(r-l+1)*d;
			modify(l,r,d);
		}else{
			int x=read(),y=read();
			if(x<y) reverse(x,y),reverse(x,y-1);
			else reverse(y,x),reverse(y+1,x);
		}
		int res=query((s+1)/2);
		write(p[res]),puts("");
	}
	return 0;
}

T4

不会。

10.30

T1

原题

考虑 dp，开个 \(g\) 存上一次第 \(i\) 个字符出现的位置，然后每次 \(f_i=f_{g_6-1}+1\)。

const int N=3e5+10;
string s;
int g[7],f[N];
signed main(){
//	freopen("114514.in","r",stdin);
//	freopen("114514.out","w",stdout);
	IOS
	cin>>s;int n=s.size();s=" "+s;
	for(rg int i=1;i<=n;i++){
		if(s[i]=='b') g[1]=i;
		if(s[i]=='e') g[6]=g[5],g[2]=g[1];
		if(s[i]=='s') g[4]=g[3],g[3]=g[2];
		if(s[i]=='i') g[5]=g[4];
		f[i]=f[g[6]-1]+g[6];
	}
	int res=0;
	for(rg int i=1;i<=n;i++) res+=f[i];
	cout<<res;
	return 0;
}

T2

原题

不妨每次把编号最小的点和其他点连边，然后启发式合并做一下完事了，复杂度 \(O(m \log^2 n)\)。

const int N=2e5+10;
int n,m;
set<int> g[N];
signed main(){
//	freopen("114514.in","r",stdin);
//	freopen("114514.out","w",stdout);
	n=read(),m=read();
	for(rg int i=1;i<=m;i++){
		int u=read(),v=read();
		if(u>v) swap(u,v);
		g[u].insert(v);
	}
	int ans=0;
	for(rg int i=1;i<=n;i++){
		if(g[i].empty()) continue;
		ans+=g[i].size();
		int u=*g[i].begin(),v=i;
		g[v].erase(g[v].begin());
		if(g[u].size()<g[v].size()) swap(g[u],g[v]);
		for(int j:g[v]) g[u].insert(j);
	}
	write(ans-m);
	return 0;
}

T3

原题

发现点有点多，考虑一下 meet in middle，这样只需分四层转移，后面忘了。

代码不放了。

T4

IOI 的题。

不会。

11.16

T1

九条可怜和Alice有一个序列，记作 \(a\)，其中有 \(n\) 个元素，编号从 \(a_1\) 到 \(a_n\)。游戏会进行若干轮直到序列中没有元素。

在每一轮中，九条可怜会先选择一个数，如果这个数是偶数，那么九条可怜的得分就会加上这个数。之后将这个数删掉。接着Alice会进行同样的操作，不同的是，如果是奇数，那么Alice的得分会加上这个数。

问两人采取最优策略的情况下，谁最后会胜利。

每次取最大的数然后判断奇偶性即可。

T2

计算序列 \(a\) 的个数，设长度为 \(m\)，满足：

\[m \neq 0 \]

\[\forall i \in [1,m),a_i<a_{i+1} \]

\[a_m \leq n \]

\[\forall i \in [1,m-2],a_i \oplus a_{i+1} \oplus a_{i+2} \neq 0 \]

忘了咋做了，贴个代码。

const int N=1e6+10;
int n,p;
int hbt[N],f[N];
signed main(){
//	freopen("114514.in","r",stdin);
//	freopen("114514.out","w",stdout);
	n=read(),p=read();
	for(rg int i=1;i<=n;i++){
		if(i&(i-1)) hbt[i]=hbt[i-1];
		else hbt[i]=i;
	}
	for(rg int i=1;i<=n;i++){
		int res=(f[i-1]+1)%p,l=hbt[i],r=i;
		while(l<r){
			int lbt=r&-r;
			int ql=(i^r^lbt)&~(lbt-1),qr=ql+lbt-1;
			res+=f[ql-1]-f[qr]+p;
			r^=lbt;
		}
		f[i]=(f[i-1]+res)%p;
	}
	write(f[n]%p);
	return 0;
}

T3

神秘 Nim 游戏，不会。

T4

不会。

11.17

100+100+35+36=271pts，rk5

T1

小模拟画立体图，有点唐。

T2

原神

子集和 dp 喜提最优解，所以说人巨常数大，人唐跑得快。

设 \(f_{S,i}\) 为只考虑前 \(i\) 位与 \(S\) 的汉明距离最大值，有 \(f_{S,i} \leftarrow \max \{f_{S,i-1},f_{S \oplus \{i\},i-1}+1\}\)，为了防止从其他数中转移过来，直接钦定为 \(-\infty\)，然后滚动数组优化一下就行了，复杂度 \(O(m 2^m)\)。

怎么没人跟我做法一样还是说这是假的只不过数据太弱了？

T3

原神

首先考虑给定一个串怎么求这个值，注意长度为偶数但是个数为奇数时无解。

发现可以看成是一些 \(1\) 的配对，显而易见的是把两个 \(1\) 交换位置一定不优所以一定是第一个和最后一个配，于是答案就出来了，设共有 \(n\) 个 \(1\)，子串长度为 \(L\)，第 \(i\) 个 \(1\) 的位置为 \(p_i\)，这里我们钦定 \(n\) 为偶数，如果是奇数可以去统计 \(0\) 即可。

\[\sum_{i=1}^\frac{n}{2}|p_i+p_{n-i+1}-(L+1)| \]

于是一个 \(O(n^3)\) 的做法就出来了。

考虑把所有 \(1\) 的位置找出来，可以从一个 \(1\) 向外扩展也可以是两个相邻的 \(1\) 向外扩展，\((x,y)\) 对区间 \([L,R]\) 的贡献为 \(|p_x+p_y-(L+R)|\)，对于奇数个\(1\) 的中间 \(1\) 的贡献可以提前 \(O(n^2)\) 预处理出来，接下来只需考虑不同的 \(1\) 的贡献如何优化。

首先对于 \((x,y)\)，考虑把 \(p_x+p_y\) 加入树状数组，维护 \(p_x+p_y\) 的和与加入的个数，可以算出 \(L \in (p_{x-1},p_x],R \in[p_y,p_{y+1})\) 的所有 \([L,R]\) 的答案，对单个 \(1\) 和相邻 \(1\) 分别都扩展一次即可。如此扩展，每对 \([L,R]\) 只会算一次，总时间复杂度 \(O(n^2 \log n)\)。

#include<bits/stdc++.h>
#define int long long
#define gc getchar
#define pc putchar
#define rg register
#define LB lower_bound
#define UB upper_bound
#define PII pair<int, int>
#define PDI pair<double, int>
#define fi first
#define se second
#define IOS ios::sync_with_stdio(0);cin.tie(0);cout.tie(0);
using db=double;using ll=long long;
using ull=unsigned long long;
using namespace std;
const ll INF=1e18;
const int inf=INT_MAX;
namespace IO{
	inline int read(){
		int x=0,f=1;
		char ch=gc();
		while(!isdigit(ch)){
			if(ch=='-') f=-f;
			ch=gc();
		}
		while(isdigit(ch)) x=(x<<3)+(x<<1)+ch-'0',ch=gc();
		return x*f;
	}
	inline void write(int x){
		if(x<0) pc('-'),x=-x;
		if(x>9) write(x/10);
		pc(x%10+'0');
	}
}
using namespace IO;
const int N=7505;
int n,c[N],cnt,ans;
char s[N];
inline int lbt(int x){return x&-x;}
struct BIT{
	int tree[N<<1];
	inline void clear(){fill(tree+1,tree+1+2*n,0);}
	inline void add(int x, int d){while(x<=2*n) tree[x]+=d,x+=lbt(x);}
	inline int query(int x){int res=0;while(x>0) res+=tree[x],x-=lbt(x);return res;}
}T1,T2;
inline void init(){
	int tmp=0;
	for(rg int i=1;i<=n;i++) tmp+=(s[i]=='G');
	if(tmp>n/2)	for(rg int i=1;i<=n;i++) s[i]=(s[i]=='H')?'G':'H';
	for(rg int L=1;L<=n;L++){
		cnt=0;
		for(rg int R=L;R<=n;R++){
			if(s[R]=='G') c[++cnt]=R;
			if((cnt&1) && ((R-L)&1)) ans--;
			else if(cnt&1) ans+=abs((L+R)/2-c[cnt/2+1]);
		}
	}
	cnt=0;
	for(rg int i=1;i<=n;i++) if(s[i]=='G') c[++cnt]=i;
	c[cnt+1]=n+1;
}
signed main(){
//	freopen("114514.in","r",stdin);
//	freopen("114514.out","w",stdout);
	scanf("%s",s+1);n=strlen(s+1);init();
	for(rg int i=2;i<cnt;i++){//odd
		T1.clear(),T2.clear();
		for(rg int x=i-1,y=i+1;x>=1 && y<=cnt;x--,y++){
			T1.add(c[x]+c[y],c[x]+c[y]);T2.add(c[x]+c[y],1);
			for(rg int L=c[x-1]+1;L<=c[x];L++){
				for(rg int R=c[y];R<c[y+1];R++){
					if((R-L)&1) continue;
					int s1=T1.query(L+R),n1=T2.query(L+R);
					int s2=T1.query(2*n)-s1,n2=T2.query(2*n)-n1;
					ans+=(n1-n2)*(L+R)-(s1-s2);
				}
			}
		}
	}
	for(rg int i=1;i<cnt;i++){//even
		T1.clear(),T2.clear();
		for(rg int x=i,y=i+1;x>=1 && y<=cnt;x--,y++){
			T1.add(c[x]+c[y],c[x]+c[y]);T2.add(c[x]+c[y],1);
			for(rg int L=c[x-1]+1;L<=c[x];L++){
				for(rg int R=c[y];R<c[y+1];R++){
					int s1=T1.query(L+R),n1=T2.query(L+R);
					int s2=T1.query(2*n)-s1,n2=T2.query(2*n)-n1;
					ans+=(n1-n2)*(L+R)-(s1-s2);
				}
			}
		}
	}
	write(ans);
	return 0;
}

T4

原神

线段树+矩阵优化本人不会，打完暴力跑路。

11.18

100+10+0+0=110pts，草泥马。

T1

几百年前的一道原题，当时本人并不会。

有一天有 \(m\) 只虱子旅行到你的头上，你非常恼火，但是限于碳基生物眼睛的范围你无法看到头顶上的虱子。

经过你和虱子谈判的结果，虱子会在 \(10^6\) 天后离去，但是这 \(10^6\) 天显然非常难熬。如果某一天第 \(i\) 只虱子在你头上活动，你的难受程度会加上 \(c_i\)。

为了定量计算你的难受程度，你和虱子首领要到了 \(n\)
条信息，每个信息可以表示为 \(L,R,K\)，以及 \(K\) 个整数 \(A_i\)，表示在 \(L\) 到 \(R\) 天范围内 \(A\) 所表示的 \(K\) 只虱子会在你头上活动。注意，如果多条信息都提到了某个虱子在某一天活动过，你这一天的难受程度还是只会计算一次。

但是不幸的是，信息在到你手上之前先经过了跳蚤手上，跳蚤为了让你不能定量计算，于是加入了一条伪造的信息。

你无法分辨哪一条是伪造的信息，因此你决定对于每条信息，如果除了这条信息以外的信息都是真的话，你的难受程度总和是多少。

有一个很典的做法，对于每只虱子分别拆贡献，做一个扫描线，记录每个虱子出现的区间然后离散化一下，区间加 \(1\) 与区间异或上信息的 \(id\)，然后对于一段区间如果只被加了一次则记录假信息的贡献，复杂度不会算，反正能过。

T2

非常有意思的题，不过赛时红温效应导致做不出来，揭示了我是废物的本质。

有一个 \(n \times n\) 的点阵，用一条直线将其分成两部分，要求直线上不能有点且直线的两侧都有点，求本质不同的分割方案数。

首先我们考虑取两个点，这两点连线的线段上没有其他点了，把它绕中点顺时针旋转一个微小的角度，一定可以得到一种分割方案。所以这种线段的数量是答案的一个下界。对于每一种分割的方案，一定存在至少一条线段使其可以通过顺时针旋转得到，所有这又是答案的一个上界。

于是答案就是任意两个可见点的连线段数量，可以 \(O(n^2)\) 枚举点对，但是 gcd 要记忆化一下不然会 T，可以用欧拉函数做到 \(O(n)\)，方队用杜教筛跑过 1e9 我没看懂，后面忘了。

\(O(n^2)\)

枚举可见线段向量的 \(x,y,x \in [0,n],y \in[0,x)\)。

n=read(),p=read();
ll ans=0;
for(rg int i=0;i<=n;i++){
	for(rg int j=0;j<i;j++){
		if(gcd(i,j)==1) ans=(ans+1ll*(n-i)*(n-j)%p)%p;
	}
}
ans=(ans*4ll%p-2ll*(n-1)%p+p)%p;
write(ans%p);
return 0;

\(O(n)\)

据说答案为：

\[2\sum_{i=1}^n(n-i)(2n-i) \varphi(i) \]

1000 年内无人能推出答案。

T3

原神

T4

忘了。

11.20

100+100+100+20+320pts。

T1

有一个值域为 \([1,m]\) 的序列 \(a\)，求 \(i,j \in [1,n]\)，\(a_i^2+a_j\) 为完全平方数的数对 \((i,j)\) 的数量。

首先值域为 \([1,m]\)，考虑求 \(x^2+y=k^2\) 的数对数，只需 \(x,y\) 在序列中出现过即可，把式子变形为 \(y=(k+x)(k-x)\)，令 \(a=k+x,b=k-x\)，可得 \(k=\frac{a+b}{2},x=\frac{a-b}{2}\)，所以我们去枚举一个因子 \(a\) 再枚举 \(a\) 的倍数 \(y\)，\(O(1)\) 判一下即可。最后答案要除以 \(2\)，因为一个 \(y\) 会被两个因子各算一次。根据调和级数，时间复杂度 \(O(m \log m)\)。

n=read(),m=read();
for(rg int i=1;i<=n;i++) v[a[i]=read()]++;
int ans=0;
for(rg int i=1;i<=m;i++){
    for(rg int k=i;k<=m;k+=i){
        int mi=min(i,k/i),mx=max(i,k/i);
        if((mx-mi)%2==0) ans+=v[k]*v[(mx-mi)/2];
    }
}
write(ans/2);
return 0;

T2

原题

首先我觉得这题不应该评紫，数据范围只有这么小一点，\(O(n^2)\) 加循环展开都能过。而且范围更大的，还推广到树上的，被我忘了的10.19T3才评蓝，评紫是何意味？

除了朴素的线段树以外本人还有新做法，考虑分治，这样我们只需求 \(L \in [l,mid],R \in [mid+1,r]\) 的满足条件的 \([L,R]\) 即可。注意到区间值域连续的充要条件是 \(mx-mi=R-L\)，这启发我们对 \([l,mid]\) 做一个后缀最值，对 \([mid+1,r]\) 做一个前缀最值，记到两个数组 \(mx,mi\) 里面。

然后我们可以分四类讨论，假设 \(mx,mi\) 都取在左区间，显然可以枚举 \(L\)，有 \(R=L+mx_L-mi_L\)，几个限制都判一下即可，右区间同理，复杂度线性。

如果 \(mx\) 在左区间，\(mi\) 在右区间，那我们要求的就是对于每一个 \(L \in [l,mid]\)，满足：

\[L+mx_L=R+mi_R \]

\[mx_L>mx_R \]

\[mi_L>mi_R \]

的 \(R \in [mid+1,r]\) 的数量。

考虑固定 \(L\)，注意到 \(mx\) 在 \([mid+1,r]\) 单调不减，\(mi\) 在 \([mid+1,r]\) 单调不增，对于上面两个不等式限制，考虑找一个最大的 \(R'\) 满足 \(mx_L>mx_R\)，与最小的 \(R''\) 满足 \(mi_L>mi_R\)。统计里面 \(L+mx_L=R+mi_R\) 的 \(R\) 个数，只需开个桶存一下即可，当 \(L\) 往左移，\(R'\) 与 \(R''\) 只会往右移，所以复杂度是线性的，\(mx\) 在右区间，\(mi\) 在左区间同理。总时间复杂度 \(O(n \log n)\)。

inline void solve(int l, int r){
	if(l==r) return;
	int mid=l+r>>1,ql,qr;
	solve(l,mid);solve(mid+1,r);
	mx[mid]=mi[mid]=a[mid],mx[mid+1]=mi[mid+1]=a[mid+1];
	for(rg int i=mid-1;i>=l;i--) mx[i]=max(mx[i+1],a[i]),mi[i]=min(mi[i+1],a[i]);
	for(rg int i=mid+2;i<=r;i++) mx[i]=max(mx[i-1],a[i]),mi[i]=min(mi[i-1],a[i]);
	for(rg int L=mid;L>=l;L--){
		int R=L+mx[L]-mi[L];
		if(R<=r&&R>mid && mx[L]>mx[R] && mi[L]<mi[R]) ans++;
	}
	for(rg int R=mid+1;R<=r;R++){
		int L=R+mi[R]-mx[R];
		if(L>=l&&L<=mid && mx[R]>mx[L] && mi[R]<mi[L]) ans++;
	}
	ql=qr=mid+1;
	for(rg int L=mid;L>=l;L--){
		while(mx[qr]<mx[L]&&qr<=r) p[mi[qr]+qr+N]++,qr++;
		while(mi[ql]>mi[L]&&ql<qr) p[mi[ql]+ql+N]--,ql++;
		ans+=p[mx[L]+L+N];
	}while(ql<qr) p[mi[ql]+ql+N]--,ql++;
	ql=qr=mid;
	for(rg int R=mid+1;R<=r;R++){
		while(mx[ql]<mx[R]&&ql>=l) p[mi[ql]-ql+N]++,ql--;
		while(mi[qr]>mi[R]&&qr>ql) p[mi[qr]-qr+N]--,qr--;
		ans+=p[mx[R]-R+N];
	}while(ql<qr) p[mi[qr]-qr+N]--,qr--;
}

T3

原题

首先看到求最大值的最小值，考虑二分，那么问题就变成了对于一个 \(mid\)，能否用小于等于 \(mid\) 的最大代价把数删完。

考虑 dp，设 \(f_{l,r}=1/0\) 为当前 \([l,r]\) 内的数能否被删完，显然是一个很傻逼的区间 dp，若 \(f_{l+1,r-1}=1\) 且 \(c(l,r) \leq mid\) 有 \(f_{l,r}=1\)，然后发现对于 \(i \in [r+2,n]\)，若 \(f_{r+1,i}=1\) 则有 \(f_{l,i}=1\)，复杂度上界应该是 \(O(n^3)\)，但是我加了神秘特判 \(f_{l,r}=0\) 使得总复杂度为 \(O(n^3 \log n)\) 的暴力跑的比 std 还快，至今不知道原因。

注意到对于 \(i \in [r+2,n]\)，若 \(f_{r+1,i}=1\) 则有 \(f_{l,i}=1\) 这个更新实际上是一个或操作，直接用 bitset 做，复杂度 \(O(\frac{n^3 \log n}{w})\)，跑的飞快。

const int N=4010;
int c[N][N],n;
bitset<N> f[N];
inline bool check(int mid){
	for(rg int i=1;i<=n;i++) f[i].reset(),f[i][i-1]=1;
	for(rg int l=n-1;l>=1;l--){
		for(rg int r=l+1;r<=n;r+=2){
			if(f[l+1][r-1]&&!f[l][r]&&c[l][r]<=mid){
				f[l][r]=1,f[l]|=f[r+1];
			}
		}
	}
	return f[1][n];
}
signed main(){
//	freopen("114514.in","r",stdin);
//	freopen("114514.out","w",stdout);
	n=read();
	for(rg int i=1;i<=n;i++){
		for(rg int j=i+1;j<=n;j+=2)
			c[i][j]=read();
	}
	int l=1,r=n*n/4,ans=0;
	while(l<=r){
		int mid=l+r>>1;
		if(check(mid)) r=mid-1,ans=mid;
		else l=mid+1;
	}
	write(ans);
	return 0;
}

T4

原题

打了个暴力跑路，突然发现还有个 bitset 优化做法，复杂度除了个 \(w\) 可以获得 45pts，感觉自己是傻逼啊。膜拜巨佬 ryh。

11.21

草泥马的忘保存了，上次写的被删完了。

T1

原题

差分一下，钦定前一半为正，后一半为负，枚举极值点，在前半段取值范围 \([A+Ci,A+Di]\)，后半段 \([B+C(n-i-1),B+D(n-i-1)]\)，判断区间有交即可，复杂度 \(O(n)\)。

T2

原题

范围小一点可以区间 dp。

考虑设 \(f_{i,j}\) 为 \(i\) 能合并出 \(j\) 的右端点（开区间），有：

\[f_{i,j}=f_{f_{i,j-1},j-1} \]

长得有点像倍增，复杂度 \(O(58n)\)，\(58=40+18\)。

T3

原题

考虑把黑子树全删掉。

考虑一条回路，答案为 \(2(n-1)\)，但是其中黑奇点和白偶点都要再操作一次，再考虑不走回路，意味着有一条简单路径上的点少走一次，非特殊点少走一次但要额外操作一次，贡献为零；特殊点少走一次还少操作一次，贡献为 \(-2\)。于是找一条包含特殊点最多的简单路径即可，复杂度 \(O(n)\)。

#include<bits/stdc++.h>
#define int long long
#define gc getchar
#define pc putchar
#define rg register
#define LB lower_bound
#define UB upper_bound
#define PII pair<int, int>
#define PDI pair<double, int>
#define fi first
#define se second
#define IOS ios::sync_with_stdio(0);cin.tie(0);cout.tie(0);
using db=double;using ll=long long;
using ull=unsigned long long;
using namespace std;
const ll INF=1e18;
const int inf=INT_MAX;
namespace IO{
	inline int read(){
		int x=0,f=1;
		char ch=gc();
		while(!isdigit(ch)){
			if(ch=='-') f=-f;
			ch=gc();
		}
		while(isdigit(ch)) x=(x<<3)+(x<<1)+ch-'0',ch=gc();
		return x*f;
	}
	inline void write(int x){
		if(x<0) pc('-'),x=-x;
		if(x>9) write(x/10);
		pc(x%10+'0');
	}
}
using namespace IO;
const int N=1e5+10;
char s[N];
int n,deg[N],val[N],u[N],v[N];
int f[N],root,num,len,tot;
bool vis[N];
vector<int> g[N],e[N];
inline void dfs(int u, int fa){
	f[u]=val[u];
	for(int v:e[u]){
		if(v==fa) continue;
		dfs(v,u);
		len=max(len,f[u]+f[v]);
		f[u]=max(f[u],f[v]+val[u]);
	}
}
inline void rebuild(){
	queue<int> q;
	for(rg int i=1;i<=n;i++) if(deg[i]==1&&s[i]=='B') q.push(i);
	while(!q.empty()){
		int u=q.front();q.pop();
		vis[u]=1;
		for(int v:g[u]){
			if(!vis[v]){
				deg[v]--;
				if(deg[v]==1&&s[v]=='B') q.push(v);
			}
		}
	}
	memset(deg,0,sizeof deg);
	for(rg int i=1;i<n;i++){
		if(!vis[u[i]]&&!vis[v[i]]){
			e[u[i]].push_back(v[i]);
			e[v[i]].push_back(u[i]);
			deg[u[i]]++,deg[v[i]]++;
		}
	}
	for(rg int i=1;i<=n;i++){
		if(vis[i]) continue;
		if((s[i]=='W'&&deg[i]%2==0)||(s[i]=='B'&&deg[i]%2==1)) val[i]=2,num++;
	}
	for(rg int i=1;i<=n;i++) if(!vis[i]) root=i,tot++;
}
signed main(){
//	freopen("114514.in","r",stdin);
//	freopen("114514.out","w",stdout);
	n=read();
	for(rg int i=1;i<n;i++){
		u[i]=read(),v[i]=read();
		g[u[i]].push_back(v[i]),g[v[i]].push_back(u[i]);
		deg[u[i]]++,deg[v[i]]++;
	}
	scanf("%s",s+1);
	rebuild();
	dfs(root,0);
	if(tot==0) return write(0),0; 
//	write(tot),pc(' '),write(num),pc(' '),write(len),puts("");
	write((tot-1)*2+num-len);
	return 0;
}

T4

原题

50pts 做法：

枚举根节点，处理出 \(d_i\) 表示 \(i\) 到根的距离，和 \(p_i\) 表示 \(i\) 到其子树内最近的叶子的距离。考虑贪心，从上往下找，如果有个点 \(d_i \geq p_i\) 则这个子树内只需一个人。

正解点分治本人不会。

11.24

100+100+100+0=300pts

T1

原题

赛时题目更简单，要求是排列。

考虑找其中最多有几个点不用操作，发现这些点一定是一条值域连续的子序列，直接 dp 即可，核心代码两行：

f[a[i]=f[a[i]-1]+1;
ans=max(ans,f[a[i]]);

T2

原题

依旧考虑最多有几个点不用操作，设 \(f_i\) 表示 \(i\) 的后缀的一段有几个点不用操作，\(l_i,r_i\) 表示颜色 \(i\) 出现的左端点和右端点，\(cnt_i\) 表示当前颜色 \(i\) 出现次数，有以下转移：

\[f_i= \max \{f_{i-1},f_{r_{a_i}+1}+cnt_{a_i}\},i=l_{a_i} \]

\[f_i=\max \{ f_{i-1},cnt_{a_i}\},i \neq l_{a_i} \]

第二个转移需要注意不能加上 \(f_{r_{a_i}+1}\)，因为这样的话相当于把 \(a_i\) 后面的颜色也都处理掉了，但是 \(i\) 前面的 \(a_i\) 还没移动，会导致转移出问题。

for(rg int i=1;i<=n;i++){
    a[i]=read();
    if(!l[a[i]]) l[a[i]]=i;
    r[a[i]]=i;
}
for(rg int i=n;i>=1;i--){
	f[i]=f[i+1],cnt[a[i]]++;
	if(i!=l[a[i]]) f[i]=max(f[i],cnt[a[i]]);
	else f[i]=max(f[i],cnt[a[i]]+f[r[a[i]]+1]);
}
write(n-f[1]);

T3

智斗程度不亚于钟离假死。

原题

一百年内无人能看懂这题。

首先神秘结论：猜出来的人一定是最大数。

然后讲一下原理，当 A 猜的时候如果另外两个人数字相等那么 A 一定是他们的和，因为值域没有 \(0\)；或者 A 可以猜他们的差，这样会来到另一个状态，这个状态数字最大的人在他那步没猜出来，说明 A 的假设错误，A 只能是他们的和。

所以可以考虑写一个递归，类似更相减损，减到两个数相等返回即可，这个状态的步数一定小于等于三。

复杂度 \(O(V \log V)\)。

#include<bits/stdc++.h>
#define int long long
#define gc getchar
#define pc putchar
#define rg register
#define LB lower_bound
#define UB upper_bound
#define PII pair<int, int>
#define PDI pair<double, int>
#define fi first
#define se second
#define IOS ios::sync_with_stdio(0);cin.tie(0);cout.tie(0);
using db=double;using ll=long long;
using ull=unsigned long long;
using namespace std;
const ll INF=2e18;
const int inf=INT_MAX;
namespace IO{
	inline int read(){
		int x=0,f=1;
		char ch=gc();
		while(!isdigit(ch)){
			if(ch=='-') f=-f;
			ch=gc();
		}
		while(isdigit(ch)) x=(x<<3)+(x<<1)+ch-'0',ch=gc();
		return x*f;
	}
	inline void write(int x){
		if(x<0) pc('-'),x=-x;
		if(x>9) write(x/10);
		pc(x%10+'0');
	}
}
using namespace IO;
const int N=505,M=3e4+10;
int t,n,cnt,pre[M],nxt[M];
inline int dfs(int x, int y, int p){
	if(x==y) return p+1;
	return (x>y)?(dfs(y,x-y,(p+2)%3)+1):(dfs(y-x,x,(p+1)%3)+2);
}
signed main(){
//	freopen("114514.in","r",stdin);
//	freopen("114514.out","w",stdout);
	t=read(),n=read();
	int fi=(t-1)%3;
	for(rg int i=1;i<n;i++) if(dfs(i,n-i,fi)==t) pre[++cnt]=i,nxt[cnt]=n-i;
	write(cnt),puts("");
	if(fi==0){
		for(rg int i=cnt;i>=1;i--) write(n),pc(' '),write(nxt[i]),pc(' '),write(pre[i]),puts("");
	}else if(fi==1){
		for(rg int i=1;i<=cnt;i++) write(pre[i]),pc(' '),write(n),pc(' '),write(nxt[i]),puts("");
	}else{
		for(rg int i=cnt;i>=1;i--) write(nxt[i]),pc(' '),write(pre[i]),pc(' '),write(n),puts("");
	}
	return 0;
}

T4

原题

不会，后面忘了。

11.25

100+0+100+100=300pts，T2 保灵是因为难度不升序排。

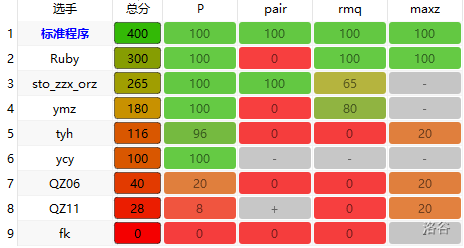
可以看到 Ruby 比我强。

T1

原题

考虑一个素因子集合 \(P=\{2,3,5,7,11,...\}\)，构造的 \(S\) 里所有数的素因子只能是这里面的，可以 \(O(k^2)\) 枚举 \(P\) 能组成的前 \(k\) 小的数，然后对于每个不达标的因子都给 \(S\) 里面其非倍数乘上这个因子直到这个因子达标，复杂度 \(O(k^2)\)，事实上 \(P\) 只取前 \(5\) 个素数即可构造出来。

#include<bits/stdc++.h>
#define int long long
#define gc getchar
#define pc putchar
#define rg register
#define LB lower_bound
#define UB upper_bound
#define PII pair<int, int>
#define PDI pair<double, int>
#define fi first
#define se second
#define IOS ios::sync_with_stdio(0);cin.tie(0);cout.tie(0);
using db=double;using ll=long long;
using ull=unsigned long long;
using namespace std;
const ll INF=2e18;
const int inf=INT_MAX;
namespace IO{
	inline int read(){
		int x=0,f=1;
		char ch=gc();
		while(!isdigit(ch)){
			if(ch=='-') f=-f;
			ch=gc();
		}
		while(isdigit(ch)) x=(x<<3)+(x<<1)+ch-'0',ch=gc();
		return x*f;
	}
	inline void write(int x){
		if(x<0) pc('-'),x=-x;
		if(x>9) write(x/10);
		pc(x%10+'0');
	}
}
using namespace IO;
int fac[5]={2,3,5,7,11};
int cnt[5];
set<int> S,T;
signed main(){
	freopen("P.in","r",stdin);
	freopen("P.out","w",stdout);
	int k=read();
	for(rg int i=1;i<=2*k*k;i++){
		int num=i;
		for(rg int j=0;j<5;j++) while(num%fac[j]==0) num/=fac[j];
		if(num==1){
			S.emplace(i);
			for(rg int j=0;j<5;j++) if(i%fac[j]==0) cnt[j]++;
			if(S.size()>=k) break;
		}
	}
	for(rg int i=4;i>=0;i--){
		T.clear();
		for(int j:S) if(j%fac[i]) T.emplace(j);
		while(cnt[i]*2<k){
			auto it=T.begin();
			int num=*it;
			T.erase(it);
			if(S.find(num*fac[i])==S.end() && num*fac[i]<=2*k*k){
				S.erase(S.find(num));
				S.emplace(num*fac[i]);
				cnt[i]++;
			}
		}
	}
	for(int i:S) write(i),pc(' ');
	return 0;
}

T2

原题

考虑按最大值分治，然后考虑两端的答案，显然由于数据不均匀，要用小的一端算大的一端防止复杂度退化。类似启发式合并，这个复杂度是 \(O(n \log n)\) 的。

然后设当前最大值为 \(a_i\)，当前计算区间一端为 \(a_j\)，我们要求另一个区间小于等于 \(\frac{a_i}{a_j}\) 的数，显然是一个主席树。

总复杂度 \(O(n \log^2 n)\)

T3

原题

首先对于每个点都有一堆区间的限制，要求这个点必须在这些区间内且在每个限制中都是 min。

对于第一个条件，显然这个点一定在所有限制的交集，这个是好做的，可以把点的存在范围缩小到一个区间，如果没有限制则默认为 \([1,n]\)。

对于第二个条件，这个点在所有一定是最小值，考虑统计每个位置有多少个区间覆盖，然后每个数从小到大贪心地放位置，这样限制是越来越松的，感性理解一下从大到小做肯定不优，因为你还要考虑更小的数不能在当前数的范围内，这样范围越来越小，不优。

具体的，枚举到一个数，给其所有区间减一，表示这个数在这些区间里放置了，把这些限制删掉；然后考虑其存在范围中有没有 \(0\)，如果没有直接判无解，因为这个区间内有更大的数做最小值，显然是无解的，否则选一个 \(0\) 的位置放这个数，再给这个位置改成 \(\infty\) 表示有数占了，这些全都可以用线段树维护，复杂度 \(O(n \log n)\)。

n=read(),q=read();
for(rg int i=1;i<=q;i++){
	int l=read()+1,r=read()+1,a=read()+1;
	v[a].emplace_back(l,r);
	if(!L[a]) L[a]=l,R[a]=r;
	else L[a]=max(L[a],l),R[a]=min(R[a],r);
}
build(1,1,n);
for(rg int i=1;i<=n;i++){
	if(L[i]>R[i]){
		for(rg int i=1;i<=n;i++) write(-1),pc(' ');
		return 0;
	}
	if(!L[i]) L[i]=1,R[i]=n;
	for(auto p:v[i]) add(1,p.fi,p.se,1);
}
for(rg int i=1;i<=n;i++){
	for(auto p:v[i]) add(1,p.fi,p.se,-1);
	PII res=query(1,L[i],R[i]);
	if(res.fi){	
		for(rg int i=1;i<=n;i++) write(-1),pc(' ');
		return 0;
	}
    ans[res.se]=i;
    add(1,res.se,res.se,inf);
}
for(rg int i=1;i<=n;i++) write(ans[i]-1),pc(' ');
return 0;

T4

原题

不难发现题目的操作就是把 \(b\) 插到 \(a\) 的空里（不包含头部），使得 \(a,b\) 两个序列都是新序列的子序列。首先考虑把取 max 操作去掉，那么 \(C\) 显然会变成：

\[\sum_{i=1}^n b_i-\sum_{i=1}^n a_i \]

然后考虑固定操作顺序，把操作的增减画成一个折线图，纵坐标是 \(C\)，横坐标是操作数，显然当没有 max 操作的时候，\(C\) 会有在 \(0\) 下面的情况，而取 \(max\) 其实对应的是给一段整体向上平移到 \(0\) 的上面，稍微思考加手模一下就能发现最终答案向上平移的长度是原图像最小值的点的负坐标，设这个长度为 \(k\)，设当前操作次数是 \(i\)，设当前用了前 \(x_i\) 个 \(a\)，前 \(y_i\) 个 \(b\)，有：

\[k= \max_{i=1}^{2n} \{\sum_{j=1}^{x_i}a_j-\sum_{j=1}^{y_i} b_j\} \]

而我们要满足的条件是 \(C+k \in [L,R]\)，显然可以考虑差分一下。然后再考虑 dp，设 \(f_{i,j}\) 为用 \(i\) 个 \(a\)，\(j\) 个 \(b\) 的方案数，注意 \(j \leq i\)。显然当 \(C+k \leq x\) 可以从 \(f_{i,j-1}\) 和 \(f_{i-1,j}\) 转移过来，复杂度 \(O(n^2)\)。

inline int solve(int x){
	memset(f,0,sizeof f);
	f[0][0]=1;
	int C=B[n]-A[n];
	for(rg int i=1;i<=n;i++){
		for(rg int j=0;j<=i;j++){
			int k=A[i]-B[j];
			if(C+k>x) continue;
			if(i>0) f[i][j]=(f[i][j]+f[i-1][j])%mod;
			if(j>0) f[i][j]=(f[i][j]+f[i][j-1])%mod;
		}
	}
	return f[n][n]%mod;
}
signed main(){
	freopen("maxz.in","r",stdin);
	freopen("maxz.out","w",stdout);
	n=read(),L=read(),R=read();
	for(rg int i=1;i<=n;i++) a[i]=read(),A[i]=A[i-1]+a[i];
	for(rg int i=1;i<=n;i++) b[i]=read(),B[i]=B[i-1]+b[i];
	write((solve(R)-solve(L-1)+mod)%mod);
	return 0;
}

11.26

100+100+100+0=300pts

T1

傻逼诈骗题骗你爸 40min。

T2

众所周知，合法车牌号必须由阿拉伯数字和大写英文字母构成，每一位共有 \(34\) 种情况。现在给你两个 \(n\) 位的车牌号 \(L,R\)，求 \([L,R]\) 中每个字符分别出现多少次。

显然是个很典的数位 dp，好像也可以直接拆贡献算。

首先满 \(i\) 位所有字符出现次数相同，有 \(f_i=34f_{i-1}+34^{i-1}\)。然后考虑统计，把数从高到低拆开，当前位不贴上界可以随便取：

for(rg int j=0;j<34;j++) cnt[x][j]=(cnt[x][j]+f[i-1]*p[x][i]%mod)%mod;//后 i-1 位的贡献
for(rg int j=0;j<p[x][i];j++) cnt[x][j]=(cnt[x][j]+g[i-1])%mod;//第 i 位的贡献

贴上界，这个上界出现的次数为数的后 \(i-1\) 位组成的数加一。

复杂度 \(O(34n)\)。

#include<bits/stdc++.h>
#define int long long
#define gc getchar
#define pc putchar
#define rg register
#define LB lower_bound
#define UB upper_bound
#define PII pair<int, int>
#define PDI pair<double, int>
#define fi first
#define se second
#define IOS ios::sync_with_stdio(0);cin.tie(0);cout.tie(0);
using db=double;using ll=long long;
using ull=unsigned long long;
using namespace std;
const ll INF=2e18;
const int inf=INT_MAX;
namespace IO{
	inline int read(){
		int x=0,f=1;
		char ch=gc();
		while(!isdigit(ch)){
			if(ch=='-') f=-f;
			ch=gc();
		}
		while(isdigit(ch)) x=(x<<3)+(x<<1)+ch-'0',ch=gc();
		return x*f;
	}
	inline void write(int x){
		if(x<0) pc('-'),x=-x;
		if(x>9) write(x/10);
		pc(x%10+'0');
	}
}
using namespace IO;
const int mod=1e9+7;
const int N=1e6+10;
string str="0123456789ABCDEFGHJKLMNPQRSTUVWXYZ";
//h->i n->o
int n,hsh[105],p[2][N];
int cnt[2][50],f[N],g[N];
char s[N];
inline void solve(int x){
	int tmp=0;
	for(rg int i=n;i>=1;i--) tmp=(tmp*34%mod+p[x][i])%mod;
//	puts("114514");
	for(rg int i=n;i>=1;i--){
		for(rg int j=0;j<34;j++) cnt[x][j]=(cnt[x][j]+f[i-1]*p[x][i]%mod)%mod;
		for(rg int j=0;j<p[x][i];j++) cnt[x][j]=(cnt[x][j]+g[i-1])%mod;
		tmp=(tmp%mod-g[i-1]%mod*p[x][i]%mod+mod)%mod;
		cnt[x][p[x][i]]=(cnt[x][p[x][i]]+tmp+1)%mod;
	}
}
signed main(){
//	freopen("114514.in","r",stdin);
//	freopen("114514.out","w",stdout);
	for(rg int i=0;i<34;i++) hsh[(int)str[i]]=i;
	n=read();
	scanf("%s",s+1);for(rg int i=1;i<=n;i++) p[0][i]=hsh[s[i]];
	scanf("%s",s+1);for(rg int i=1;i<=n;i++) p[1][i]=hsh[s[i]];
	reverse(p[0]+1,p[0]+1+n);reverse(p[1]+1,p[1]+1+n);
	g[0]=1;
	for(rg int i=1;i<=n;i++){
		f[i]=(f[i-1]*34%mod+g[i-1])%mod;
		g[i]=g[i-1]*34%mod;
	}
	solve(0);solve(1);
	for(rg int i=0;i<34;i++){
		int res=count(p[0]+1,p[0]+1+n,i);
		write(((cnt[1][i]%mod-cnt[0][i]%mod+mod)%mod+res)%mod),pc(' ');
		if(str[i]=='H'||str[i]=='N') write(0),pc(' ');
	}
	return 0;
}

T3

原题

评黑纯恶评。

首先不难发现奇数位一定要是奇数，偶数位一定要是偶数。然后发现一次合法的操作会使全局逆序对数 \(-3\)，使奇位或偶位的逆序对数 \(-1\)，所以全局逆序对数是奇偶逆序对数之和的三倍。上面两个是必要条件。

充分性的话，发现只交换三元组的 \(1,3\) 位一定可以把序列排成有序的，因为有效的操作一定会使奇偶逆序对数之和 \(-1\)。假设存在一种符合条件的情况无解，那么一次交换会使逆序对数减小 \(<3\)，说明存在一次交换使逆序对数减少 \(>3\)，显然不可能。

于是树状数组做一下就好了，复杂度 \(O(n \log n)\)。

T4

不会。

11.27

最后一次模拟赛。

在最后的这一次，我不知道有什么想说的。总的算下来我也打过这么多模拟赛了。从今年寒假开始写模拟赛记录到现在，写了有 6 篇，这些文章见证了我从啥都不会到现在能打两三百分的历程。

可能是因为本人素质比较低，写了不少脏话。

学了这么久的 OI，如今可能真的迎来终点了？我很后悔，我为什么要学竞赛？为了它我失去了尊严，失去了优异文化课成绩，失去了一个好的身体，失去了一段美好的感情，失去了纯洁，失去了天真，失去了善良，失去了半个青春……

可能小学三年级我就不应该答应我妈学编程，可能我应该像 HOT 的那些唐氏小朋友一样天天打游戏然后退学，可能我应该再考烂点让我妈看不见我进复赛的希望，可能我应该再多抄点题解让洛谷把我封号使我破防，可能我不应该认识过氧化氢，可能我应该在初中放弃它去和 wmy 好好交往，可能我应该像那些社会人一样不务正业，可能我不应该去学什么竞赛也不去考什么 qzez，可能我应该选其他竞赛然后发现自己是个废物然后提前退役学习文化课，可能……

但是这些都不可能了，我始终相信这些选择一定不比现实更优。

NOIP2025 RP++

100+60+100+20=280pts。

T1

平面直角坐标系上有 \(2n\) 个点 \(P_{1∼2n}\)。

对于每个 \(i\)，你可以选择令 \(A_i=P_{2i−1},B_i=P_{2i}\) 或 \(A_i=P_{2i},B_i=P_{2i−1}\)。

然后，你可以从任意点出发，在任意点结束，要求依次标记 \(A_1,A_2,A_3,⋯,A_n;B_n,⋯,B_3,B_2,B_1\)（当位于某个点时可以选择标记它）。

每次移动只能让某一维坐标 \(±1\)，求所需的最小移动次数。

不难发现 \(P_{2n-1}\) 和 \(P_{2n}\) 分别对应 \(A_n,B_n\)，这两个点间的曼哈顿距离显然是要算的。然后倒着 dp 一下即可，比较唐。

inline int dist(PII a, PII b){return abs(a.fi-b.fi)+abs(a.se-b.se);}
signed main(){
//	freopen("114514.in","r",stdin);
//	freopen("114514.out","w",stdout);
	n=read();
	for(rg int i=1;i<=2*n;i++) p[i].fi=read(),p[i].se=read();
	PII A=p[2*n],B=p[2*n-1];
	f[n][0]=f[n][1]=dist(A,B);
	for(rg int i=n-1;i>=1;i--){
		PII P=p[2*i],Q=p[2*i-1];
		f[i][0]=min(f[i+1][0],f[i+1][1])+dist(A,P)+dist(B,Q);
		f[i][1]=min(f[i+1][0],f[i+1][1])+dist(A,Q)+dist(P,B);
		A=P,B=Q;
	}
	write(min(f[1][0],f[1][1]));
	return 0;
}

T2

忘取模挂了 40pts。

IMO 2011 D1T1。

规定一个四元组 \((a,b,c,d)\) 合法，当且仅当 \(a,b,c,d\) 都是正整数且 \(a<b<c<d\)。

定义一个四元组的神奇度，为从中选出两个不同元素之和为 \(a+b+c+d\) 的因数的方案数。

求从给定区间 \([l,r]\) 内选择数构成四元组，所得神奇度为 \(4\) 的方案数，对 \(998244353\) 取模。

证明

先证明这个神奇度最大为 \(4\)，令 \(a+b+c+d=S\)，由于 \(a<b<c<d\)，于是 \(b+d,c+d>\frac{S}{2}\)，这两个不可能为 \(S\) 的因数，所以最大只能是 \(4\)。

然后由于 \(a+d,b+c \mid S\) 且 \(a+b+c+d=S\)，而这两个必有一个大于等于 \(\frac{S}{2}\)，所以只能 \(a+d=b+c\)。

令 \(a+b=u,a+c=v,u<v\)，有 \(2(u+v-2a)=S\)，因为 \(u,v \mid S\)，于是有：

\[v \mid 2(u-2a) \]

\[u \mid 2(v-2a) \]

由于 \(u<v\)，可得：

\[1 \leq \frac{2(u-2a)}{v} <2 \]

所以 \(v=2(u-2a)\)，代入可得 \(u \mid 2(2u-6a)=4u-12a\)，所以 \(u \mid 12a\)。

分讨：

\(u=3a,v=2a\) 舍。

\(u=4a,v=4a\) 舍。

\(u=6a,v=8a\)，此时根据 \(a+d=b+c\)，\((a,b,c,d)=(a,5a,7a,11a)\)。

\(u=12a,v=20a,(a,b,c,d)=(a,11a,19a,29a)\)。

所以可以直接 \(O(1)\) 求出答案。

const int mod=998244353;
signed main(){
//	freopen("114514.in","r",stdin);
//	freopen("114514.out","w",stdout);
	int T=read();
	while(T--){
		int l=read(),r=read();
		write((max(r/11-l+1,0ll)%mod+max(r/29-l+1,0ll)%mod)%mod);
		puts("");
	}
	return 0;
}

T3

给定一个可重集合，求其所有 非空子集内数的和 的中位数。

首先考虑任意子集，它和它的补集一定是一个正数第 \(k\) 名，一个倒数第 \(k\) 名，所以中位数就是两个和最接近的互补子集中和比较大的那个，也就是大于等于 \(\frac{1}{2} \sum S_i\) 的第一个子集。显然这是一个 01 背包问题，复杂度 \(O(nW)\)，直接用 bitset 优化一下就过了。

const int N=2e3+10;
const int M=4e6+10;
int n;
signed main(){
//	freopen("114514.in","r",stdin);
//	freopen("114514.out","w",stdout);
	bitset<M> b;
	n=read(),b=1;
	int sum=0;
	for(rg int i=1;i<=n;i++){
		int x=read();
		sum+=x,b|=(b<<x);
	}
	sum=(sum+1)/2;
	b>>=sum;
	int pos=b._Find_first();
	write(sum+pos);
	return 0;
}

T4

原题

难晕了，不会。

后记

谨以此文送给将来 qzez 的 OIer 们，当你们找不到模拟赛的 tj 就来这里，本文将同步发表到 luogu。

\[End. \]