【Quant102】如何计算 N 日斜率

一元线性回归的斜率公式是：

\[k = \frac{(x - \bar{x})^T (y - \bar{y})}{\|x - \bar{x}\|^2} \]

由于斜率具有平移不变性，x通常取 0 到窗口大小减一。

def slope(df, close_col='close', slope_col='slope', window=5, inplace=True):
    if not inplace: df = df.copy()
    x = np.arange(window, dtype='f')
    x -= x.mean()
    x_sq_sum = (x ** 2).sum()
    df[slope_col] = df[close_col].rolling(window) \
        .apply(lambda y: ((y - y.mean()) * x).sum() / x_sq_sum)
    return df

向量化版本使用sliding_window_view代替rolling.apply。

sliding_window_view创建给定数组的一个滑动窗口视图。其中每个元素被替换为该元素在给定轴上的给定大小的滑动窗口。如果原数组的形状为[d0, ..., d(n-1)]，新数组的形状为[d0, ..., di - window + 1, ..., d(n-1), window]，其中i为滑动窗口所在的轴，window为窗口大小。新数组的元素[idx0, ..., idx(i), ..., idx(n-1), j]映射到原数组的[idx0, ..., idx(i)+j, ..., idx(n-1)]。

from numpy.lib.stride_tricks import sliding_window_view

def slope(df, close_col='close', slope_col='slope', window=5, inplace=True):
    if not inplace: df = df.copy()
    x = np.arange(window, dtype='f')
    x -= x.mean()
    x /= (x ** 2).sum()
    y = sliding_window_view(df[close_col], window, -1)
    slope = ((y - y.mean(-1, keepdims=True)) * x).sum(-1)
    df[slope_col] = np.concatenate([np.full(window - 1, np.nan), slope])
    return df

测试：

import pandas as pd
import numpy  as np
from matplotlib import pyplot as plt
df = pd.DataFrame({'close': np.random.randint(-1000, 1000, [100])})
slope(df)
df.slope = df.slope.shift(-2)
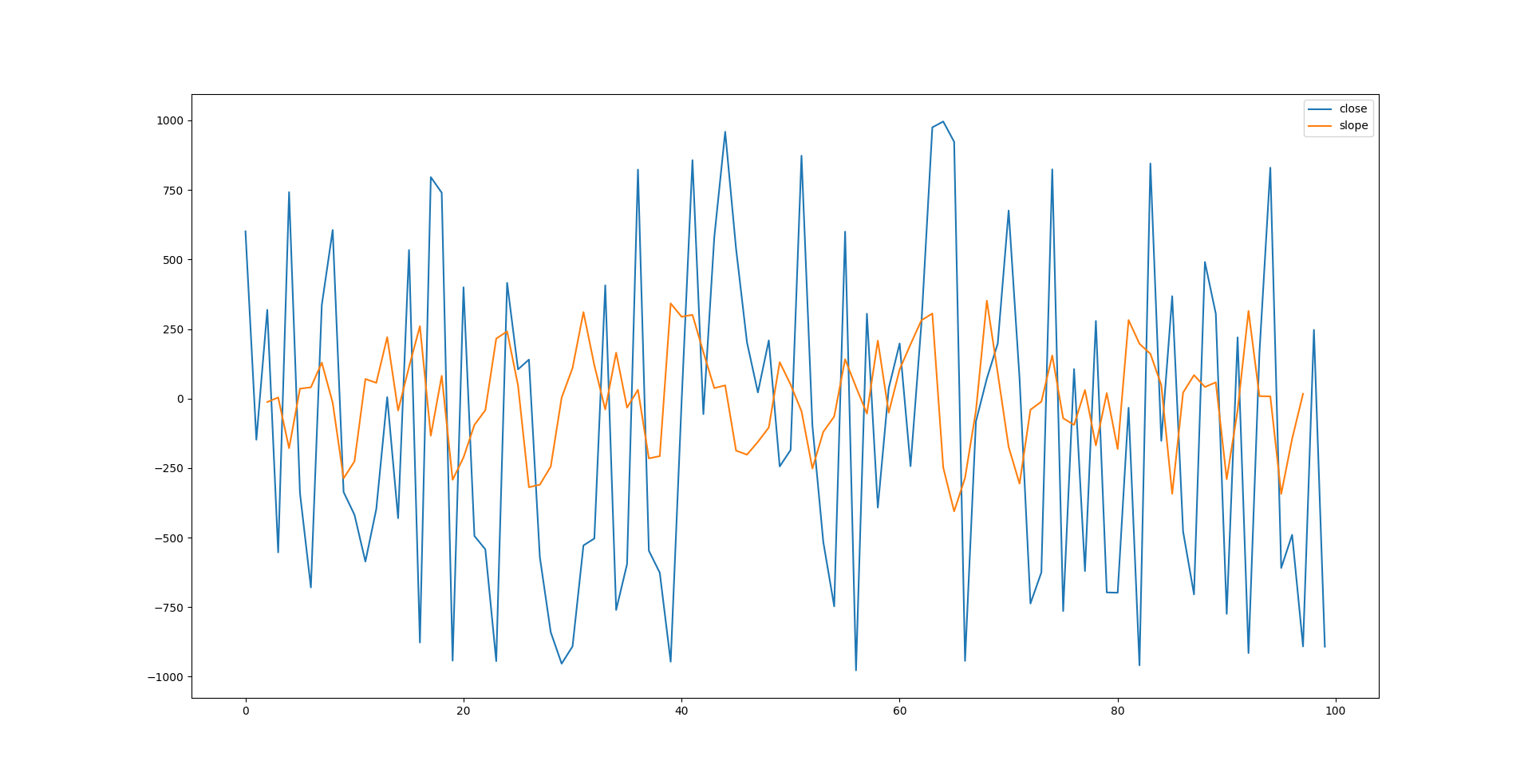
df.plot()
plt.show()