Halcon基础——图像增强

图像增强

定义

分类

空间域

频率域

点运算

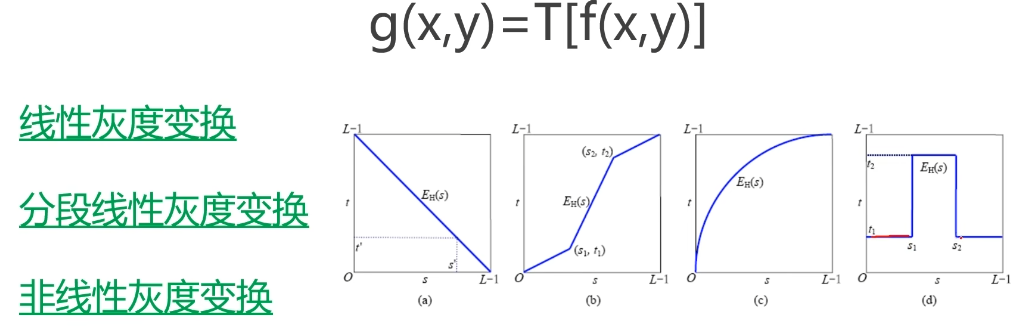
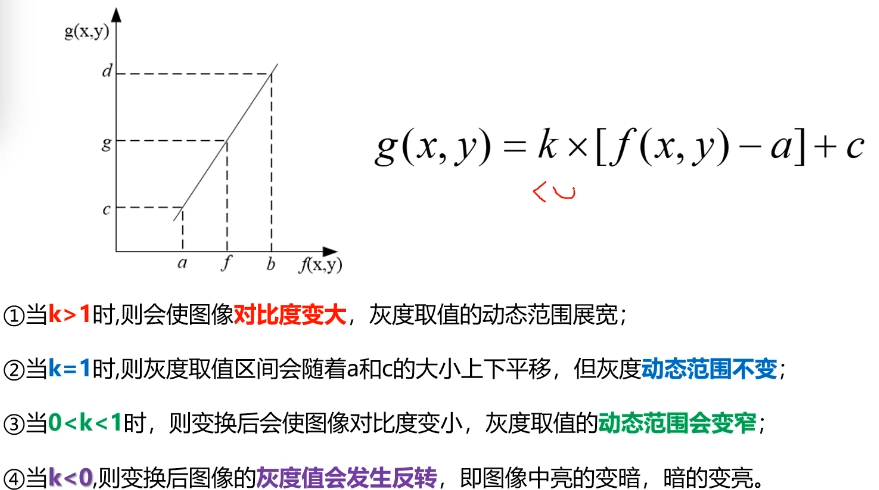
线性灰度变换

使用一个线性函数去改变灰度值

分段线性灰度变换

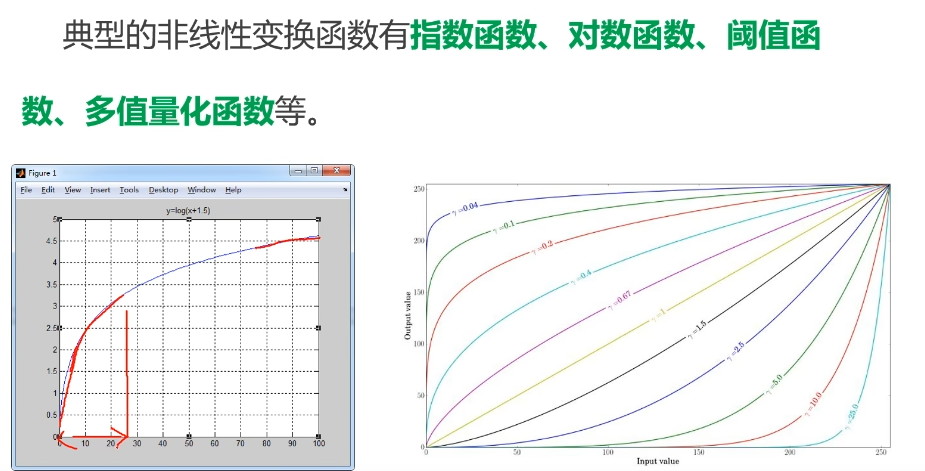
非线性灰度变换

Halcon的点运算

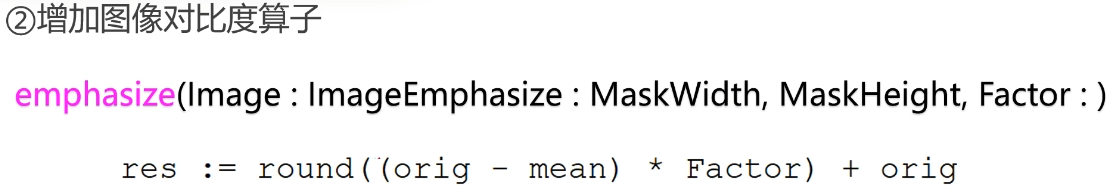
直方图修正法

基于图像的灰度直方图进行修正。

直方图均衡化

让图像灰度分布更加均匀。

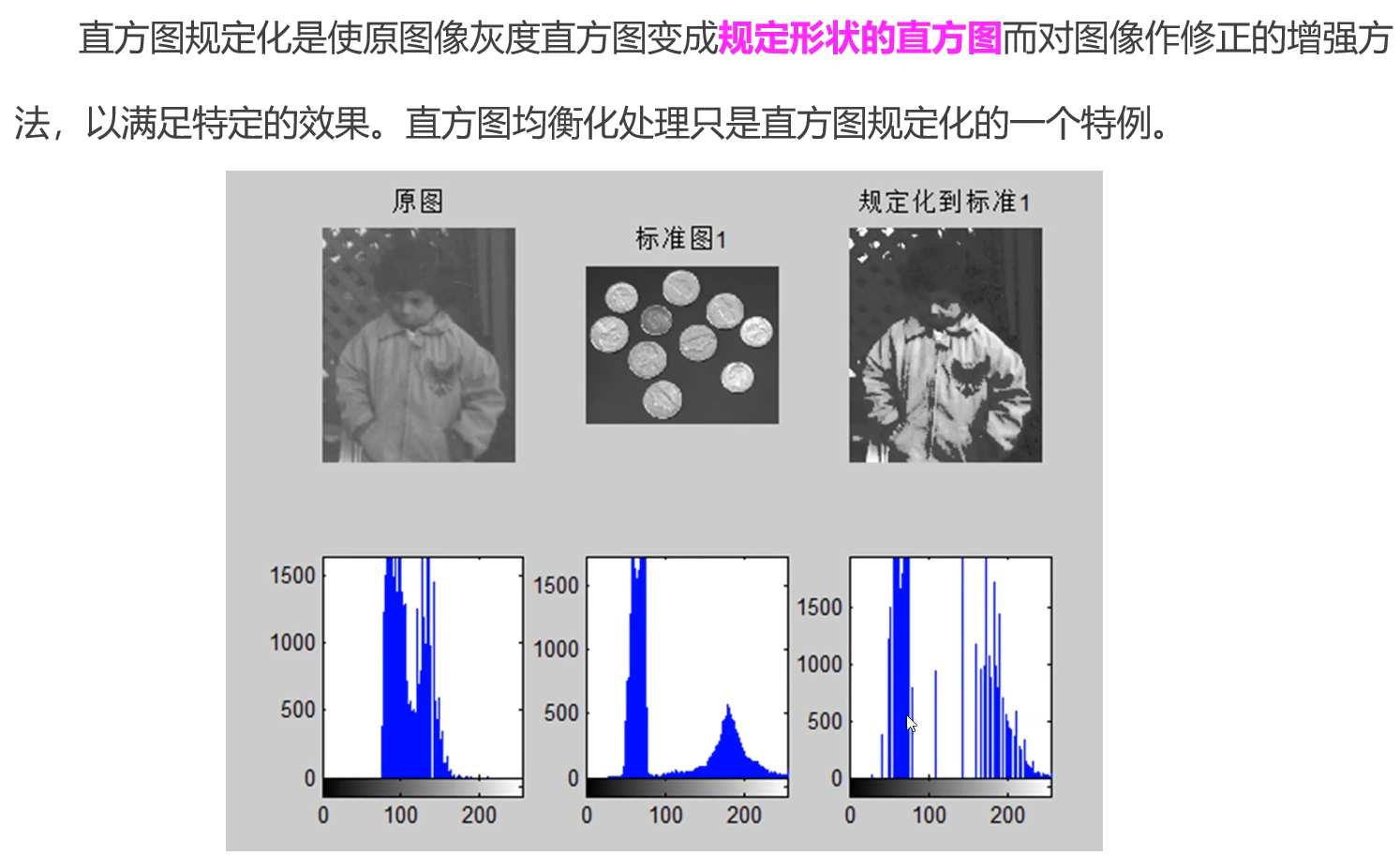
直方图规定化

经处理后，左侧图像灰度直方图类似于右侧图像。

图像平滑

噪声

高斯噪声

椒盐噪声

均值滤波

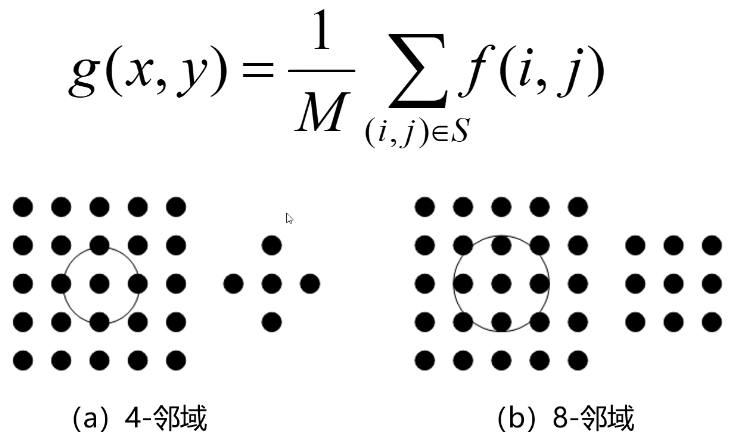
为了能够确认出中心点，掩膜的Size要设置为奇数。

中值滤波

取指定掩膜中，灰度的中值，作为当前点的灰度值。
中值滤波对于椒盐噪声有很好的去噪效果。

多图像平均法

拍摄多幅图像后，然后将图像累加后取平均值。原因：使用电子设备拍摄的图像中的噪声多为高斯噪声，其对应的数学期望为0.因此取多幅图像计算平均值，能够降低噪声。

图像锐化

图像边缘提取

假设我们获取一条扫描线上的所有灰度值，那么其对应的灰度图像如下图所示。

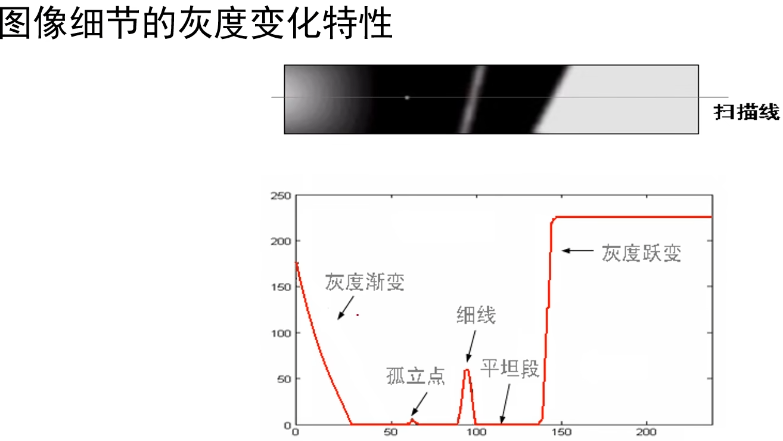
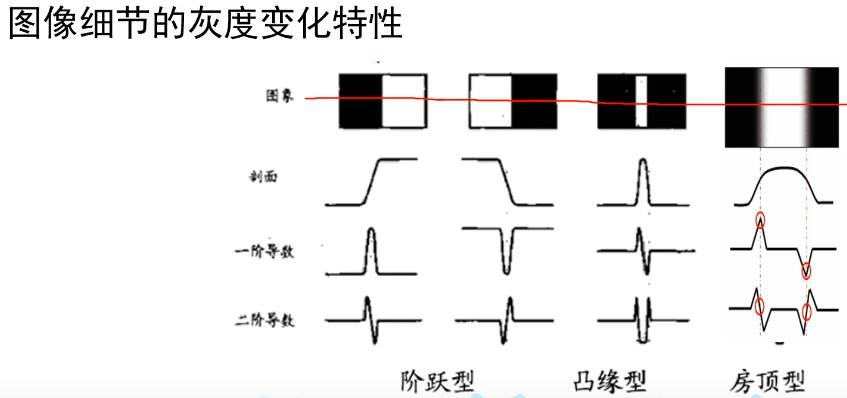
对于一阶导数而言，边缘出现在其导数的极值处。并且对应二阶导数的零点。

数学原理

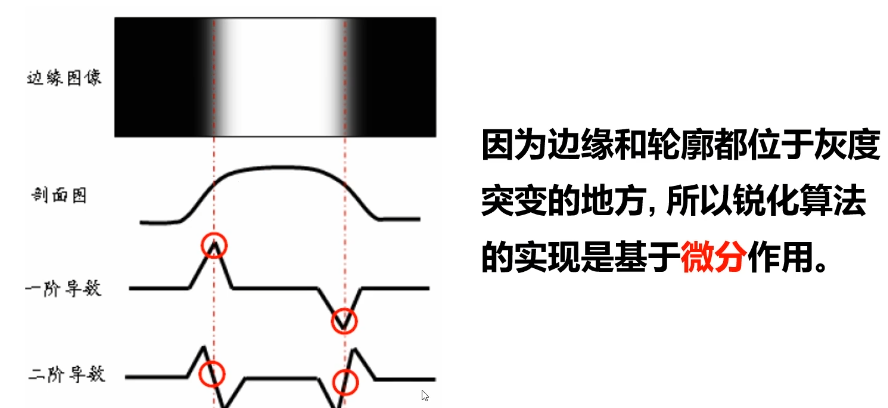
如何在图像上求导数呢？首先要明确图像上的像素点都是离散的，实际上我们的求导是用差分去表示微分。例如在x方向上导数的计算公式如下。

边缘检测算子

上面讲到，我们既可以通过一阶导数去判断边缘，也可以通过二阶导数去判断边缘。根据采取的方法不同分为以下两类方法。

梯度法

在模拟图像中，在理想条件下。对于图像函数f(x,y)其应该是处处可导的。

在实际情况中，我们还是选择使用差分去代替上面的求导。从中我们分别可以得到x和y方向的导数公式。近似得到梯度。

将上述公式转换为一个模板即可得到。

横向微分运算

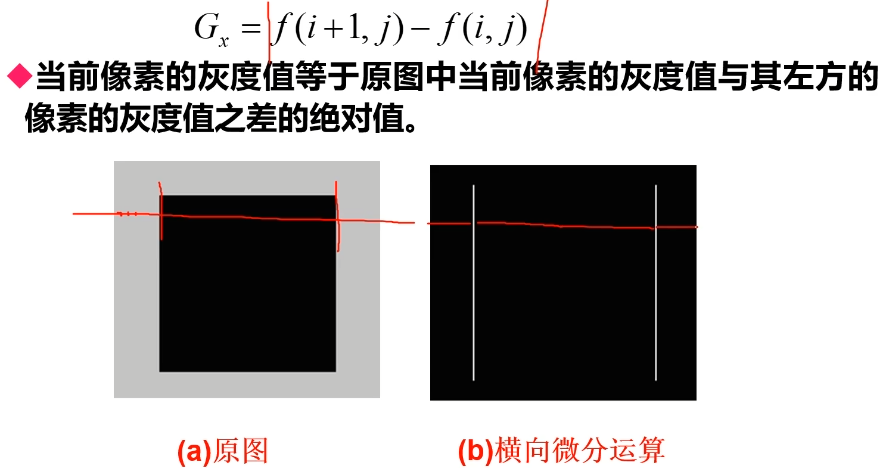
纵向微分运算

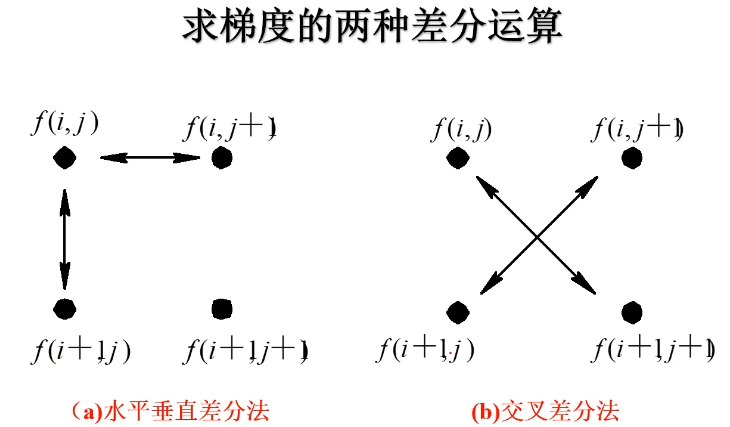
双方向一次微分运算

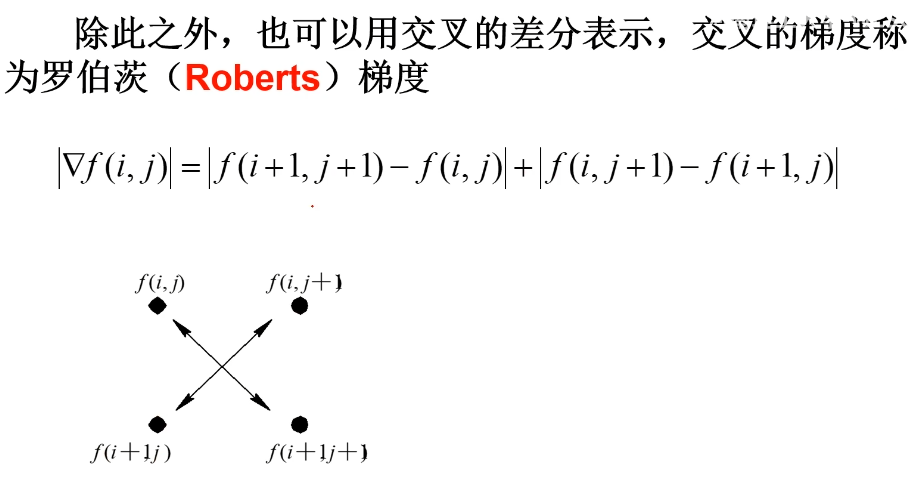
交叉差分运算

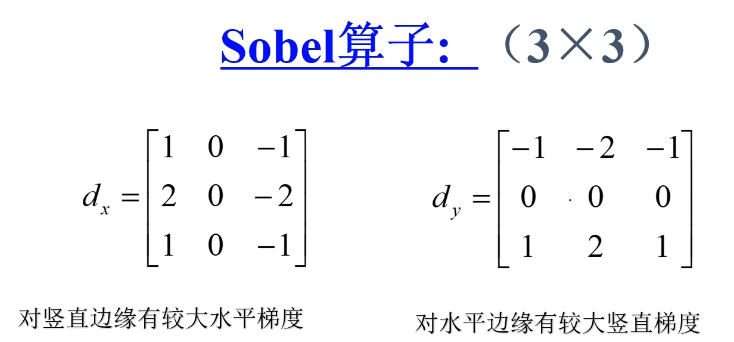
Sobel算子（一阶微分）

上面的两种方法（双方向、交叉），在实际应用过程中，非常容易收到噪声的干扰，导致边缘提取不准确。

Sobel算子通过大中心位置的权重以及感受野，能够实现更好的边缘提取效果。

下图中，使用Sobel算子，我们更能直观体会到增强后的人的轮廓。

Halcon中使用Sobel算子

该算子的返回结果是一张幅值强度图像。
其中，FilterType规定了幅值的计算方式，通常采用绝对值相加的方式即可。Size用于设置算子模板的大小。
需要明确的是，使用算子提取的所谓边缘，是基于灰度的变化进行的，也即是说提取的边缘是一条灰度的过渡带。这是我们往往还需要搭配skeleton算子，才能获取到一条细致的边缘轮廓。

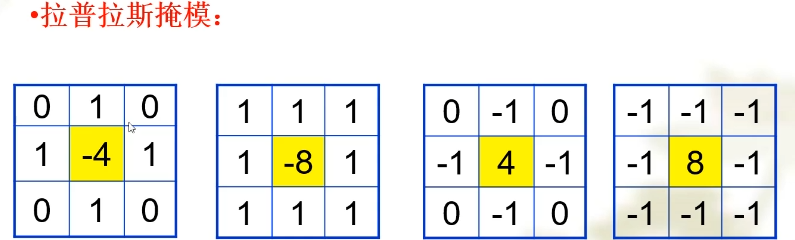
拉普拉斯增强算子（二阶微分）

此类算子就是通过计算二阶导数进行边缘增强。通过计算二阶导的梯度，实现边缘增强。

不同的掩膜实际上就规定了算子能够检测的边缘方向，例如 如果图像中仅包括水平和垂直的边缘，那么选择4邻域的掩膜即可。如果还包含斜边，就应该考虑使用8邻域的掩膜

Halcon中使用拉普拉斯算子

需要明确的是，该算子返回的图像，仅仅是通过拉普拉斯算子滤波后的一个二阶导数图像。根据上面的分析可以，边缘对应着二阶导为0的点，因此图像中的边缘实际上是值为0的地方。如果想要提取边缘，还需要使用zero_crossing_sub_pix等算子，去找出为0的像素点，这才是真正的边缘
更多情况下，我们使用的是laplace_of_gauss算子，该算子会首先进行一次高斯滤波降噪。