"影石Insta360杯"2025牛客暑期多校训练营10 Problem J. 线段 (segments)

题面

题解

这个题显然不是让你直接去干，所以我们尝试分讨来慢慢找规律。

• \(3\) 个点以下的时候，显然无解，欧氏空间不存在三个直角的等边三角形，也不存在全是直角的线段。

• \(4\) 个点的时候，正方形是最显然的解。这个解是唯一的，具体可以考虑构造一个直角，边上的两个点必然需要在其垂平面内寻找下一个点，那么这个交出来只有一个点，因此只有一组解。
  
  

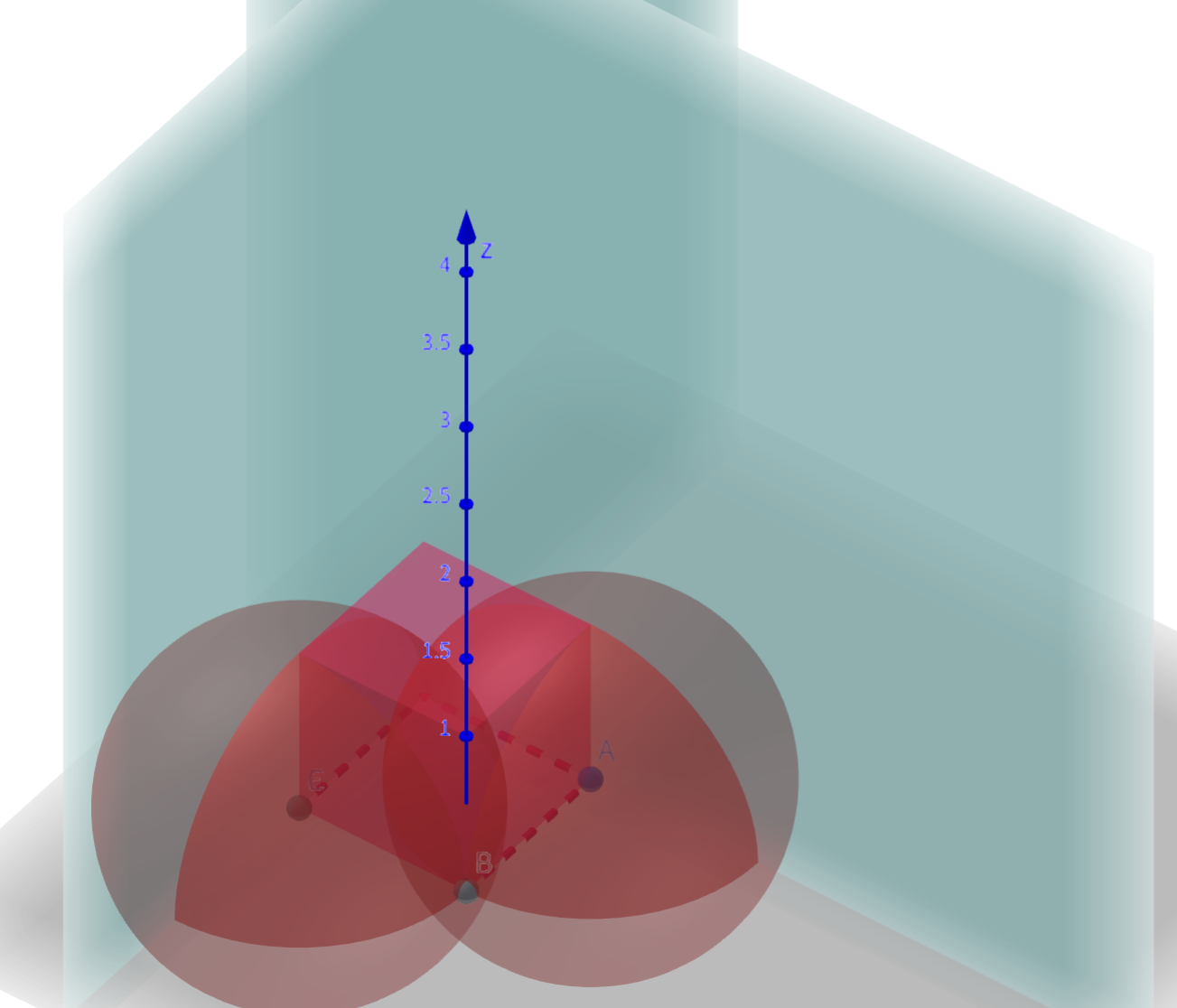
• \(5\) 个点的时候，开始有一点复杂，按照刚才的思路，我们可以造出两个动点，如下图 \(J, \, K\) 两点，当且仅当过 \(J\) 和 \(K\) 做的垂平面交线为 \(J, \, K\) 时有解，显然合法的两个平面是 \(J, \, K\) 所在圆的公切面上，这是唯一的，可知 \(\vec{JK} \parallel xOy\)，此时 \(\vert \vec{JK} \vert = \sqrt{2}\)，不符合答案，因此无解。
  
  

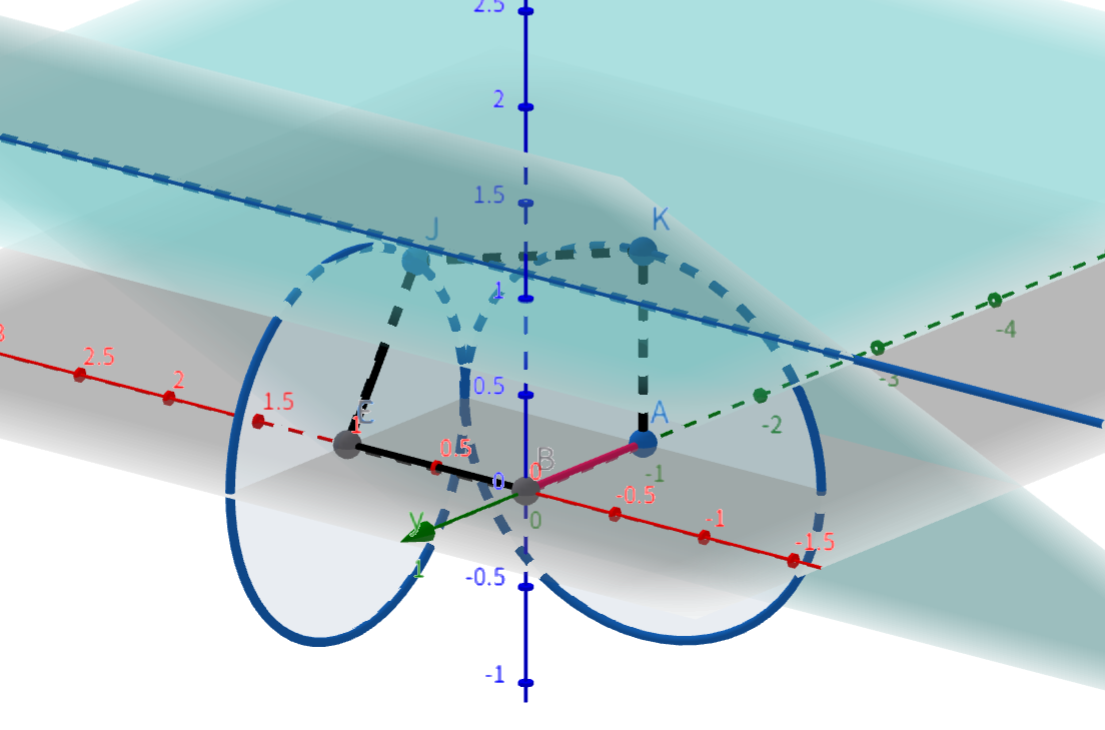
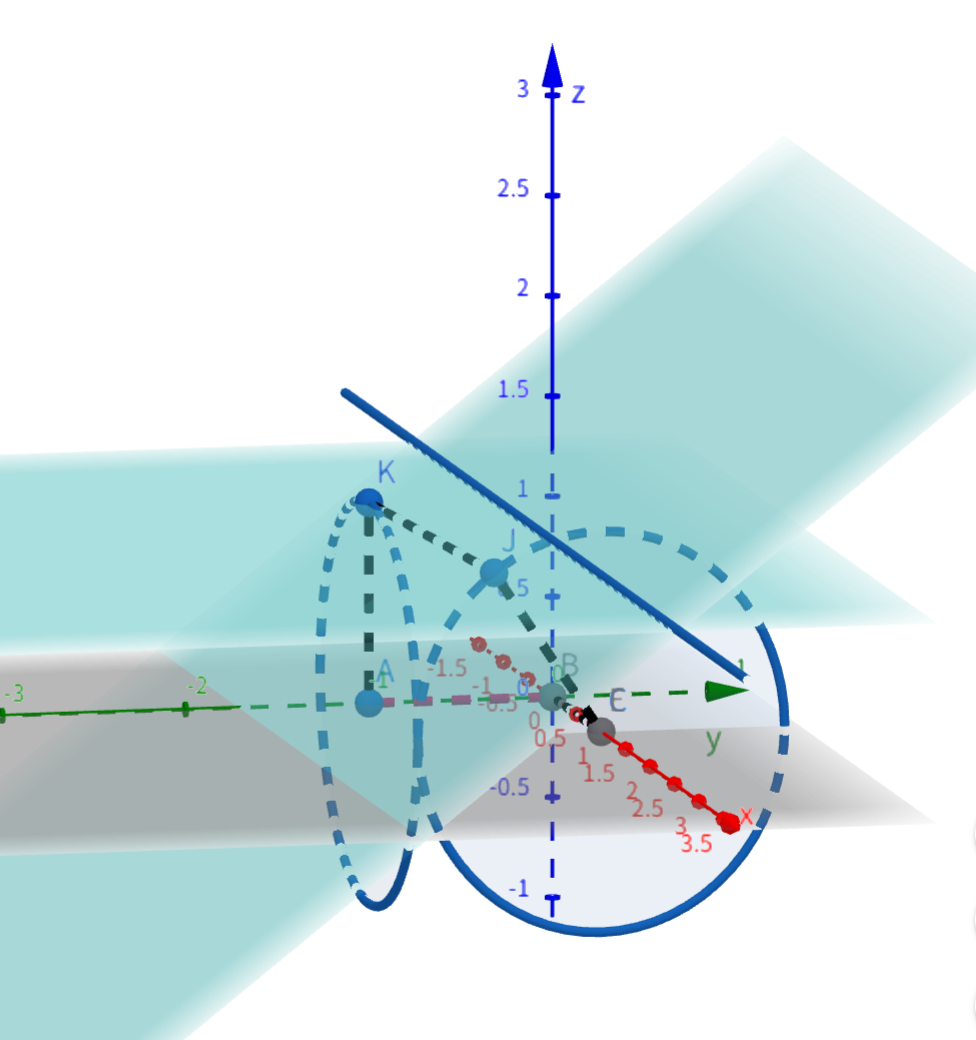
• \(6\) 个点的时候，不难想到的是正方体的一个框架，如下图。不过这个结论我们可以进一步推广。
  
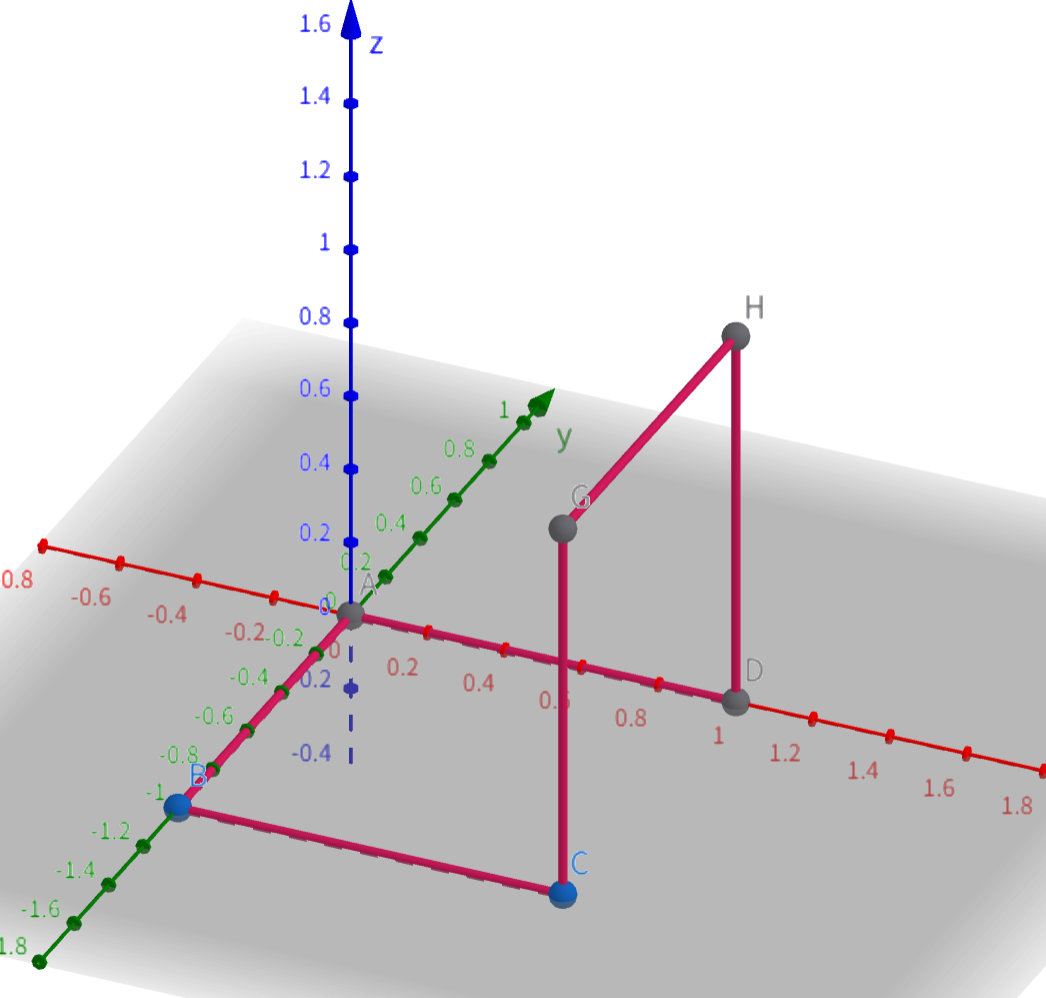
  我们考虑刚才 \(5\) 个点的情形，\(\vec{DE}\) 始终平行于 \(xOy\)，我们找到 \(\vec{DE}\) 的中点 \(F\) 并做垂平面，两个以 \(D, \, E\) 为圆心，半径为 \(1\) 的球在垂平面上始终会交出一个以 \(F\) 为圆心的圆，考虑 \(\vert \vec{DE} \vert\) 的取值范围至少可以为 \([0, \, 2]\)，因此存在 \(\vert \vec{DE} \vert = \sqrt{2}\)，使得存在一点 \(K\) 满足 \(\triangle DKE\) 是等腰直角三角形，那么 \(K\) 在圆上旋转一圈的所有情况都是异构的，因此 \(n = 6\) 有无数组解。
  

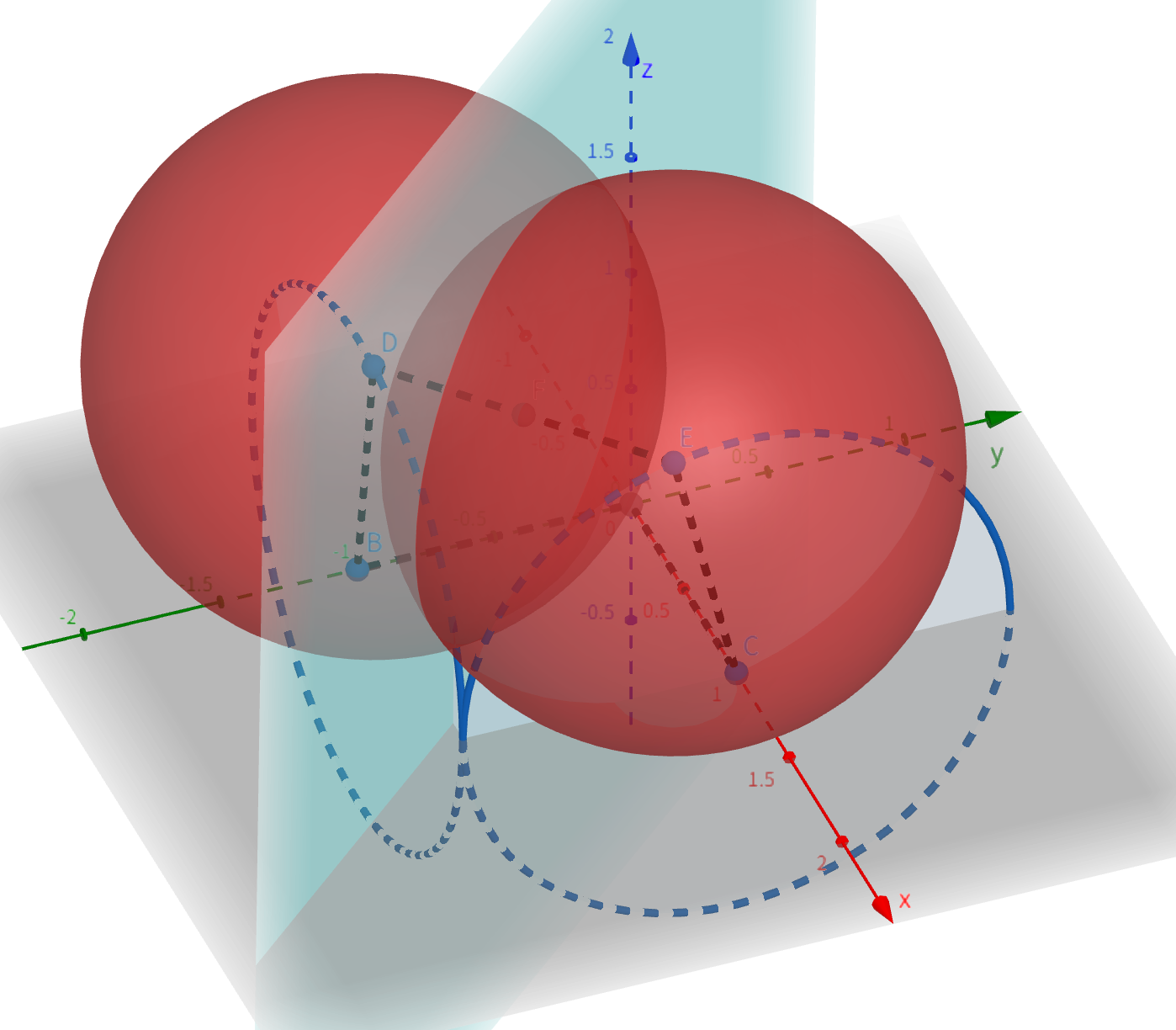
• \(n > 6\) 时，考虑 \(n = 6\) 的构造情况，如下图构造出 \(A, \, B, \, C, \, D, \, E, \, G\) 六点。
  
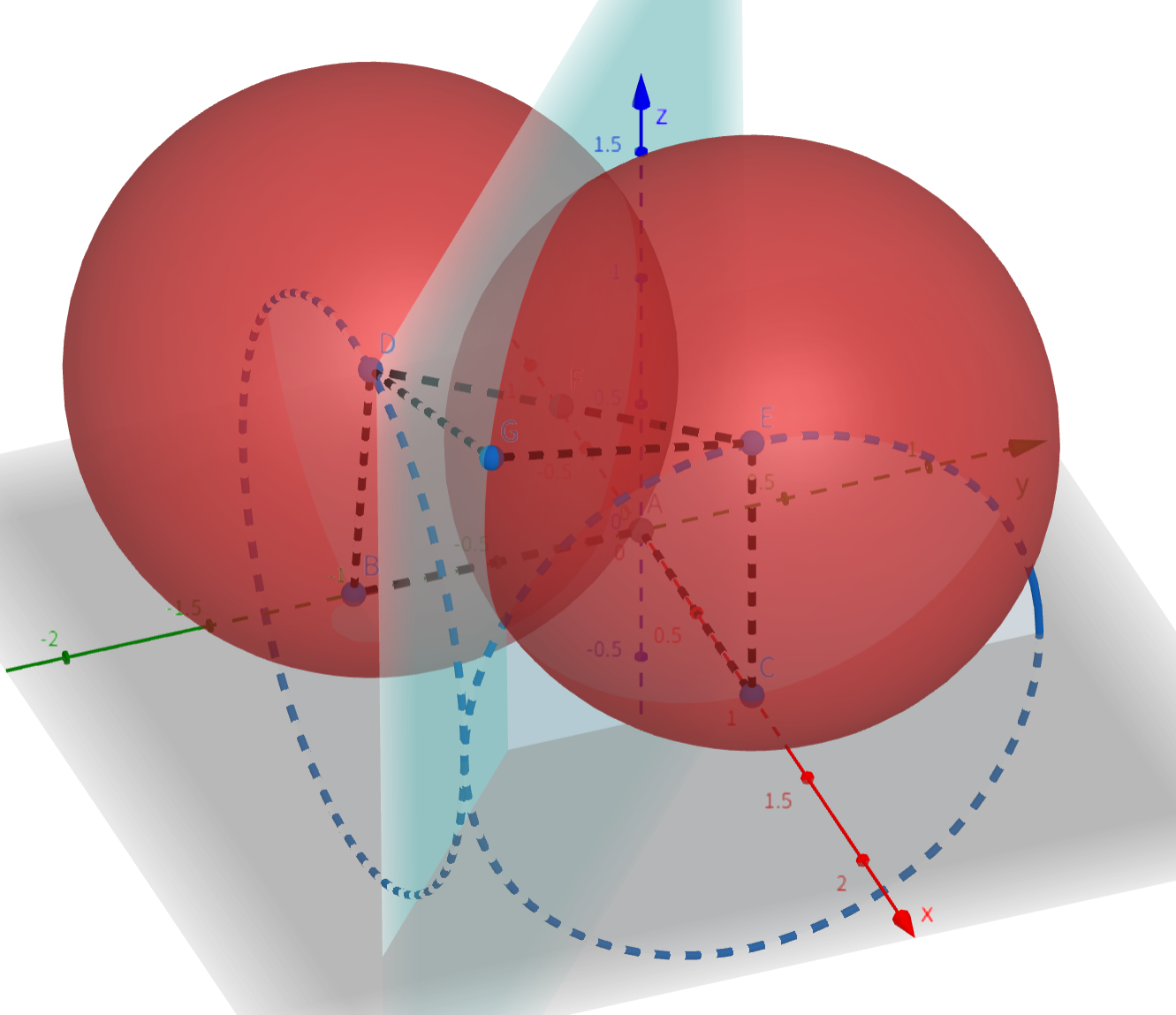
  根据我们之前的讨论，此时把 \(D, \, E, \, G\) 平替为 \(D, \, E, \, G, \, H\) 正方形是一组合法的解。
  
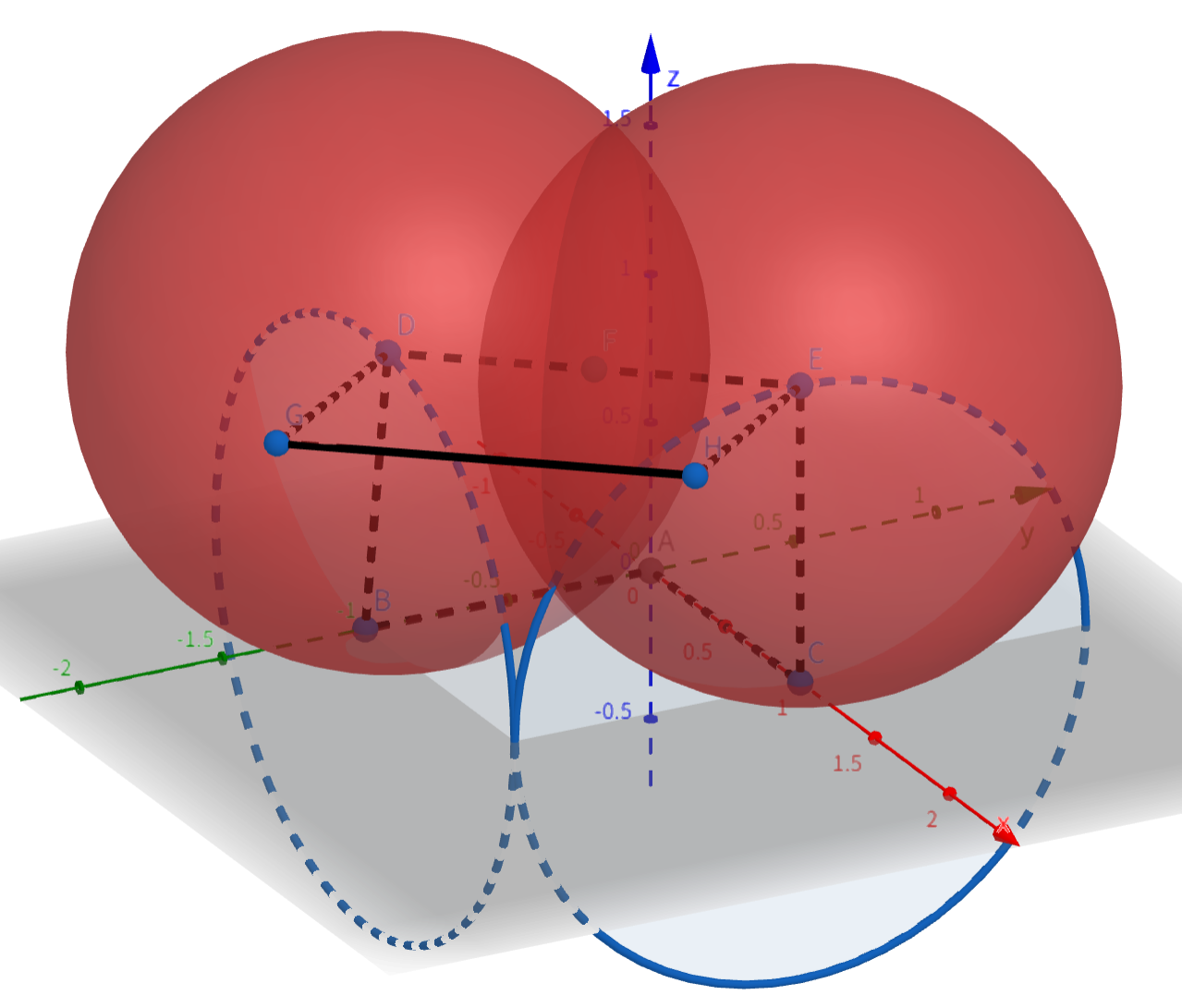
  我们考虑将正方形扭曲，将下图中交出的 \(H\) 点视作一组解（\(G\) 移动至 \(H\)），\(G\) 点可以随着 \(D\) 点和 \(F\) 点的旋转在圆上适配出其他的 \(H\) 点，因此我们有无数组解。
  
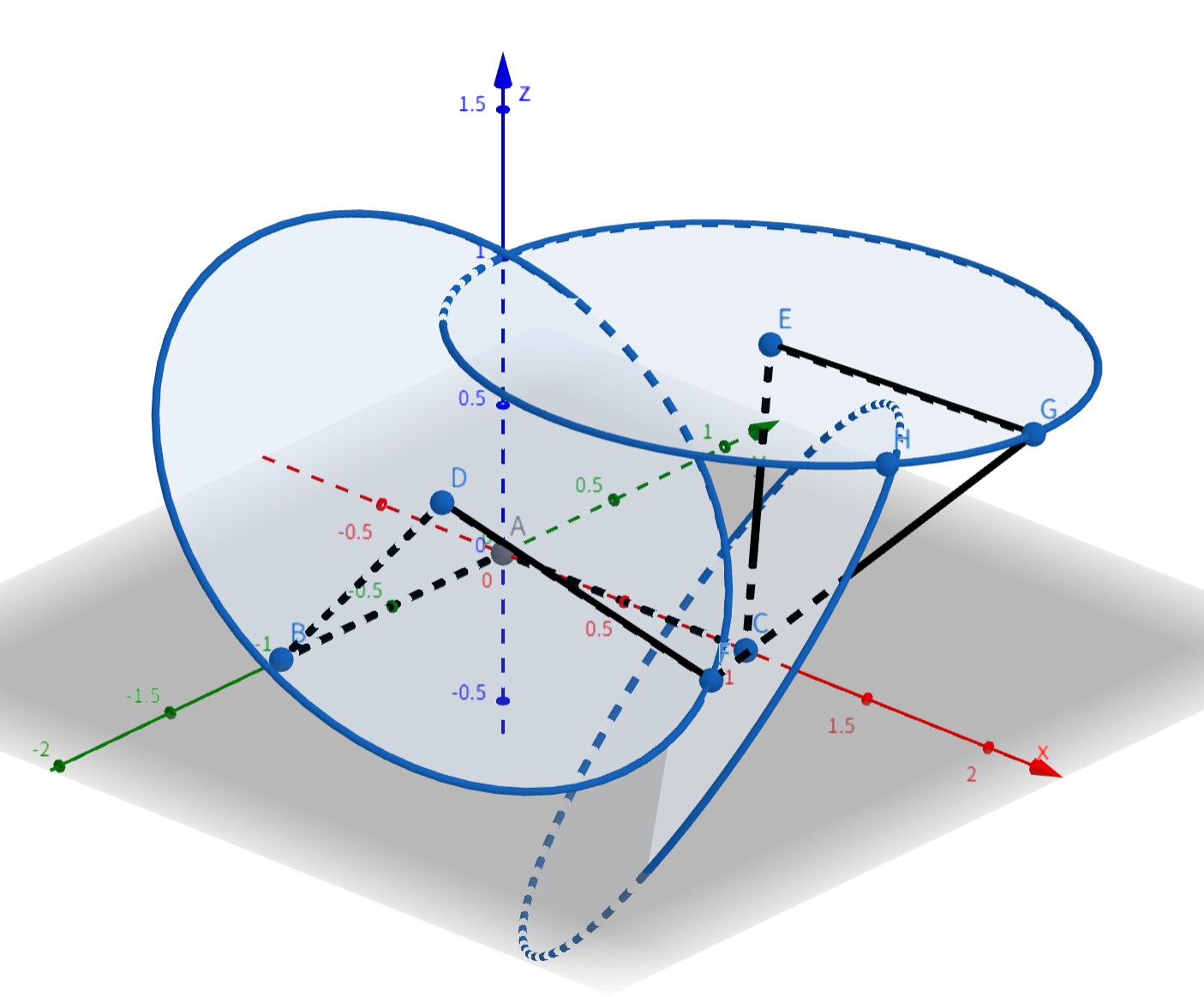
  更大的情况，重复选择中点做垂平面交相邻两点做球的圆可以求出新的 \(K'\) 点，如此重复，容易得知 \(n > 6\) 时有无限解。当然感性理解也是可以的，因为 \(n = 6\) 有无数解，\(n\) 更大的时候只会更松弛，因此也是无限解。

考虑答案如何输出，答案为偶数显然，按模 \(4\) 转圈即可，然后输出 \(n = 4, \, 6\) 的解。

• \(n = 7\) 的时候，按照如下图方式构造，其中底部是一个正方形，平面 \(DFG\) 平行于平面 \(xOy\)。
  

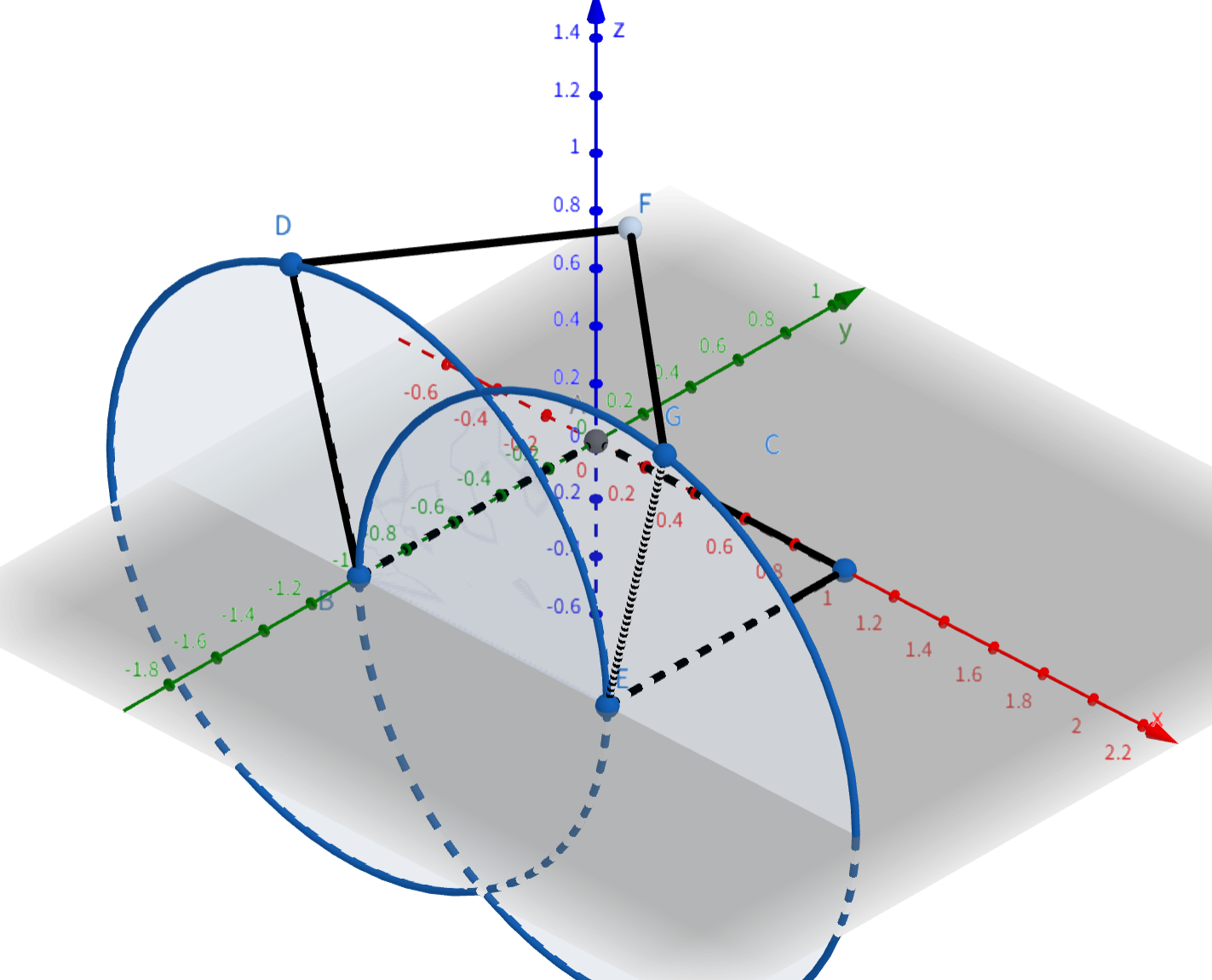
设方程联立可以解出（按顺序编号）：
\(A(0, \, 0, \, 0)\)
\(B(1, \, 0, \, 0)\)
\(C(1, \, \frac{1 - \sqrt{2}}{2}, \, \sqrt{\frac{1 + 2\sqrt{2}}{4}})\)
\(D(1 - \frac{2\sqrt{2} - 1}{\sqrt{7}}, \, \frac{1}{2}, \, \frac{3 + \sqrt{2}}{2\sqrt{1 + 2\sqrt{2}}})\)
\(E(1, \, \frac{1 + \sqrt{2}}{2}, \, \sqrt{\frac{1 + 2\sqrt{2}}{4}})\)
\(F(1, \, 1, \, 0)\)
\(G(0, \, 1, \, 0)\)

同理，\(n = 9\) 的情况只用在 \(\vec{AG}\) 那边拼一个正方形即可。

如上，本题完。

#include<bits/stdc++.h>
using namespace std;
#define ll long long
#define ld long double
#define ull unsigned long long
#define PII pair<ll, ll>
#define pb push_back
#define clr(f, n) memset(f, 0, sizeof(int) * (n))
#define cpy(f, g, n) memcpy(f, g, sizeof(int) * (n))
#define rev(f, n) reverse(f, f + (n))
const int N = 2e5 + 10, _G = 3, mod = 998244353, INF = 1e9;
const ld sq2 = sqrt(2), a = 1 - (2 * sq2 - 1) / sqrt(7), b = (3 + sq2) / sqrt(4 + 8 * sq2), c = sqrt(1 + 2 * sq2) / 2;
ld point[9][3] = {{0, 0, 0},
                  {1, 0, 0},
                  {1, (1 - sq2) / 2, c},
                  {a, 0.5, b},
                  {1, (1 + sq2) / 2, c},
                  {1, 1, 0},
                  {0, 1, 0},
                  {0, 1, 1},
                  {0, 0, 1}};

void solve() {
    int n, m; cin >> n, m = n;
    cout.precision(10);
    if (n <= 3 || n == 5) return cout << "-1\n", void();
    if (n % 2 == 0) {
        while (n > 6) {
            n -= 4;
            cout << point[0][0] << " " << point[0][1] << " " << point[0][2] << "\n";
            cout << point[1][0] << " " << point[1][1] << " " << point[1][2] << "\n";
            cout << point[5][0] << " " << point[5][1] << " " << point[5][2] << "\n";
            cout << point[6][0] << " " << point[6][1] << " " << point[6][2] << "\n";
        }
        cout << point[0][0] << " " << point[0][1] << " " << point[0][2] << "\n";
        cout << point[1][0] << " " << point[1][1] << " " << point[1][2] << "\n";
        cout << point[5][0] << " " << point[5][1] << " " << point[5][2] << "\n";
        cout << point[6][0] << " " << point[6][1] << " " << point[6][2] << "\n";
        if (n == 6) cout << point[7][0] << " " << point[7][1] << " " << point[7][2] << "\n";
        if (n == 6) cout << point[8][0] << " " << point[8][1] << " " << point[8][2] << "\n";
    } else {
        while (n > 9) {
            n -= 4;
            cout << point[0][0] << " " << point[0][1] << " " << point[0][2] << "\n";
            cout << point[1][0] << " " << point[1][1] << " " << point[1][2] << "\n";
            cout << point[5][0] << " " << point[5][1] << " " << point[5][2] << "\n";
            cout << point[6][0] << " " << point[6][1] << " " << point[6][2] << "\n";
        }
        cout << point[0][0] << " " << point[0][1] << " " << point[0][2] << "\n";
        cout << point[1][0] << " " << point[1][1] << " " << point[1][2] << "\n";
        cout << point[2][0] << " " << point[2][1] << " " << point[2][2] << "\n";
        cout << point[3][0] << " " << point[3][1] << " " << point[3][2] << "\n";
        cout << point[4][0] << " " << point[4][1] << " " << point[4][2] << "\n";
        cout << point[5][0] << " " << point[5][1] << " " << point[5][2] << "\n";
        cout << point[6][0] << " " << point[6][1] << " " << point[6][2] << "\n";
        if (n == 9) cout << point[7][0] << " " << point[7][1] << " " << point[7][2] << "\n";
        if (n == 9) cout << point[8][0] << " " << point[8][1] << " " << point[8][2] << "\n";
    }
    if (m == 4) cout << "1\n";
    else cout << "inf\n";
}

int main() {
    ios::sync_with_stdio(false);
    cin.tie(0), cout.tie(0);
    int T = 1;
    cin >> T;
    while (T -- ) solve();
    return 0;
}