相似对角化与合同对角化的关系
本博客仅做个人经验性总结,非学习笔记,是在学习完两者后做的一个区分。
相似矩阵
定义
在一组基 \(C = (c_1, c_2, \ldots, c_n)\) 下,向量 \(s = (s_1, s_2, \ldots, s_n)^T\) 具有坐标 \(x = (x_1, x_2, \ldots, x_n)^T\),此时 \(s = Cx\) 。
考虑一个变换矩阵 \(A_{n \times n}\),使得 \(s'\) 为 \(s\) 在基 \(C\) 下关于 \(A\) 的映射,即 \(s' = As\),我们也有 \(s = Cx, s' = Cx'\),我们可以把 \(A_{n \times n}\) 直接作用于坐标上,即 \(s' = CAx = Cx'\) 。
现在我们有一组新基 \(D = (d_1, d_2, \ldots, d_n)\),我们希望求得在基 \(D\) 下 \(s\) 的坐标 \(y = (y_1, y_2, \ldots, y_n)^T\),这很容易,因为 \(s = Cx = Dy\),我们解一个非齐次线性方程组即可得出 \(y\) 。
我们知道 \(s'\) 在基 \(C\) 下从 \(s\) 映射而来的变换矩阵 \(A\),如何求出在基 \(D\) 下从 \(s\) 映射而来的变换矩阵 \(B\) 呢?
设 \(P\) 为基变换矩阵,根据基变换公式:
容易求出 \(P = C^{-1}D\),进而得出 \(y = Px\),带入 \(s' = DBy = CAx\) 有:
所以我们可以得出重要结论:
因此 \(A\) 和 \(B\) 描述了 \(n\) 维线性空间上同一个线性变换,这种变换是客观存在的,但可以使用不同的基从不同的矩阵进行描述,在不同基下描述同一个线性变换的矩阵称作相似矩阵,即 \(A \sim B\),上述表达式 \(B = P^{-1}AP\) 就是相似矩阵的表达式。
已知某线性变换在基 \(C = (c_1, c_2, \ldots, c_n)\) 下的矩阵是 \(A\),求该线性变换在基 \(D\) 下的矩阵 \(B\) 。
我们首先求出 \(C\) 到 \(D\) 的基变换矩阵 \(P\)。
根据 \(D = CP \to P = C^{-1}D\),使用公式 \(B = P^{-1}AP\) 即可得到相似矩阵 \(B\) 。
性质
-
反身性:\(A \sim A\)
-
对称性:若 \(A \sim B\),则 \(B \sim A\)
-
传递性:若 \(A \sim B\),\(B \sim C\),则 \(A \sim C\)
-
单位阵相似唯一性:单位阵 \(E\) 只与自身相似
-
若 \(A \sim B\),则两者具有相同的特征多项式。
-
证明:
\(B = P^{-1}AP \to \lvert \lambda E - B \rvert = \lvert \lambda E - P^{-1}AP \rvert\)
\(\begin{aligned} \lvert \lambda E - P^{-1}AP \rvert &= \lvert P^{-1} (\lambda E)P - P^{-1}AP \rvert \\ &= \lvert P^{-1} (\lambda E - A)P \rvert\\ &= \lvert P^{-1} \rvert \lvert \lambda E - A \rvert \lvert P \rvert \\ &= \lvert \lambda E - A \rvert \end{aligned}\)这进而推出了更多的性质,此时 \(A\) 和 \(B\) 的特征多项式各个系数均相等,对比对应两者 \(\lambda^{n - 1}\) 的系数和常数项,可知:
\[tr(A) = tr(B) \]\[\lvert A \rvert = \lvert B \rvert \]更进一步,两者特征方程相同,特征根相同, 有:
\[\lambda_A = \lambda_B \]
-
-
若 \(A \sim B\),如果一方可逆,另一方一定可逆
-
若 \(A \sim B\),则 \(A^{*} \sim B^{*}\)
-
证明:
\(B^{*} = (P^{-1} A P)^{*} = P^{*} A^{*} (P^{-1})^{*}\)
而 \(P^{*} = P^{-1} \lvert P \rvert\)
\(\to (P^{-1} \lvert P \rvert) A^{*} (P \lvert P^{-1} \rvert) = P^{-1} A^{*} P\)容易发现伴随矩阵的基变换矩阵也是 \(P\),两者伴随矩阵相似。
-
-
若 \(A \sim B\),则 \(A^T \sim B^T\)
-
证明:
\(\begin{aligned} B = P^{-1}AP \to B^T &= (P^{-1}AP)^T \\ &= P^T A^T (P^{-1})T \\ &= P^T A^T (P^T)^{-1} \\ \end{aligned}\)该矩阵的基变换矩阵为 \(P^T\),两者转置矩阵也相似。
-
-
若 \(A \sim B\),则 \(kA \sim kB\),\(A^m \sim B^m\),\(p(A) \sim p(B)\)
- 证明较为显然,故略过
-
若 \(A \sim B\),则 \(r(B) = r(A)\)
因为基变换矩阵相当于行和列的线性运算,不改变其空间大小,所以他们的秩是相同的。
我们列出一个表格来总结一些性质:
| 矩阵 | \(A\) | \(A^T\) | \(A^{-1}\) | \(A^{*}\) | \(p(A)\) | 迹 | 行向量 | 特征根和特征向量 |
|---|---|---|---|---|---|---|---|---|
| 基变换矩阵 | \(P\) | \((P^T)^{-1}\) | \(P^{-1}\) | \(P\) | \(P\) | - | - | - |
| 性质 | \(\sim\) | \(\sim\) | \(\sim\) | \(\sim\) | \(\sim\) | \(tr(A) = tr(B)\) | \(\vert A \vert = \vert B \vert\) | \(\lambda_A = \lambda_B, \, X_A = X_B\) |
相似对角化
定义
\(n\) 阶方阵 \(A\) 经过 \(n\) 阶可逆矩阵 \(X\) 的相似变换成为对角矩阵 \(U = X^{-1}AX\) 这一过程称作相似对角化。
因为对角矩阵的优秀性质,他的线性运算相当于各个坐标关于基的线性运算,仅仅具有倍数关系,我们令 \(U = \operatorname{diag}(\lambda_1, \lambda_2, \ldots, \lambda_n), X = (x_1, x_2, \ldots, x_n)\),\(x_i\) 为列向量。
可以看出
如果 \(A\) 通过可逆矩阵 \(X\) 的相似变换成为了对角阵 \(U\),那么 \(U\) 的各个元素就是的 \(A\) 的特征值,\(X\) 的各列就是 \(A\) 的特征向量。
这样,对角化问题转化为了求特征值和特征向量问题。但是 \(A\) 和 \(U\) 未必相似,因为 \(X\) 未必可逆,也就是说,相似特征化的前提条件是 \(X\) 可逆。
合同变换
定义
对二次型 \(f = x^T A x\),其中 \(A\) 为实对称矩阵(因为实对称矩阵是唯一的)。
二次型的秩定义为 \(r(f) = r(A)\) 。
对两组二次型做基变换,如下图所示:
| 二次型 | 基向量组 | 坐标 |
|---|---|---|
| \(f = x^T A x\) | \(C = (c_1, c_2, \ldots, c_n)\) | \(x\) |
| \(f = y^T B y\) | \(D = (d_1, d_2, \ldots, d_n)\) | \(y\) |
设基向量组 \(C\) 到 \(D\) 的基变换矩阵为 \(P\),则 \(P\) 可逆且 \(x = Py\) 。
我们称 \(B = P^T A P\) 为合同变换。
不同基向量组下表示同一个二次型的实对称矩阵是一组合同矩阵,其中对应的合同变换矩阵是对应的基变换矩阵,它一定可逆。
对于 \(n\) 维线性空间下同一个二次型,不同基向量下,对应的实对称矩阵具有合同关系。
实对称矩阵
定义
如果方阵 \(A\) 满足 \(A = A^T\),则称 \(A\) 为对称矩阵。
如果一个对称矩阵内的所有元素都是实数,那么称其为实对称矩阵,也就是 \(A = A^T = \overline{A}\) 。
性质
复数运算可以扩展到矩阵:
-
实对称矩阵的特征值都是实数
实对称矩阵的特征向量都是实向量-
证明:
根据 \(A = A^T = \overline{A}\) 和 \(Ax = \lambda x(x \neq 0)\),我们推导下列式子,因为点乘运算等价于转置乘原行向量:
\[\begin{aligned}\lambda(\overline{x} · x) &= \lambda(\overline{x}^Tx) = \overline{x}^T(\lambda x) \\ &= \overline{x}^T(Ax) = \overline{x}^TA^Tx = (A\overline{x})^Tx \\ &= (\overline{A}\overline{x})^Tx = (\overline{Ax})^Tx \\ &= (\overline{\lambda x})^Tx = (\overline{\lambda}\overline{x})^Tx = \overline{\lambda}(\overline{x}^Tx) \\ &= \overline{\lambda}(\overline{x} · x)\end{aligned} \]这说明 \(\overline{\lambda} = \lambda\),即 \(\lambda \in \mathbb{R}\)
-
-
实对称矩阵的特征向量两两正交
-
证明:
考虑 \(\lambda_1x_1 = Ax_1\),\(\lambda_2x_2 = Ax_2(\lambda_1 \neq \lambda_2)\),有:\[\begin{aligned}\lambda_1(x_1 · x_2) &= \lambda_1(x_1^Tx_2) = (\lambda_1x_1)^Tx_2 = (Ax_1)^Tx_2 \\ &= x_1^TA^Tx_2 = x_1^T(Ax_2) = x_1^T(\lambda_2x_2) = \lambda_2x_1^Tx_2 \\ &= \lambda_2(x_1 · x_2)\end{aligned} \]\((\lambda_1 - \lambda_2)(x_1 · x_2) = 0 \to x_1 · x_2 = 0\)
因此实对称矩阵的特征向量两两正交,也说明了实对称矩阵的几何重数等于代数重数,实对称矩阵一定可以相似对角化,这个性质比线性无关更强,下面我们会用到。
-
合同对角化
选择合适的可逆矩阵 \(P\),使 \(A\) 经过合同变换后变为对角阵 \(U = P^T A P\),这样就可以使某个一般形态的二次型化为只含有平方项的特殊二次型,这个过程叫合同对角化。
如下列案例:
此时取 \(y_1 = x_1 + x_2\),\(y_2 = x_2\) 可以得到:
使用配方法可以将任意一个二次型化为只含平方项的形式,这种形式叫做二次型的标准型,即任意二次型都可化为标准型。
利用基变换矩阵:
根据基变换公式 \(x = Py\),利用合同变换可以得到 \(U = P^T A P\)。
如果我们令 \(f = 1\),容易发现,上述两个方程均代表了一个椭圆方程:
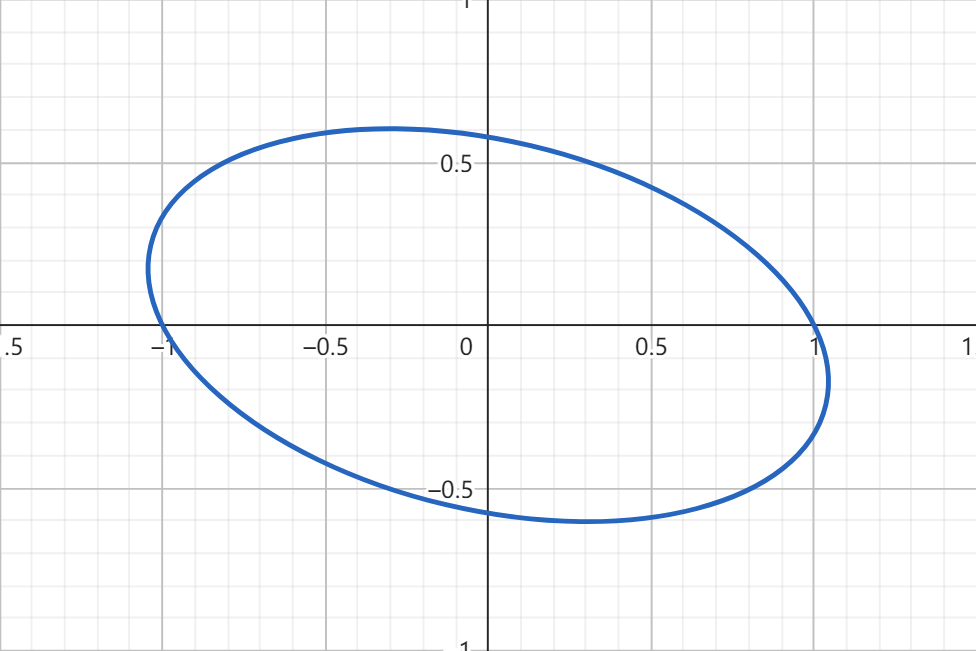
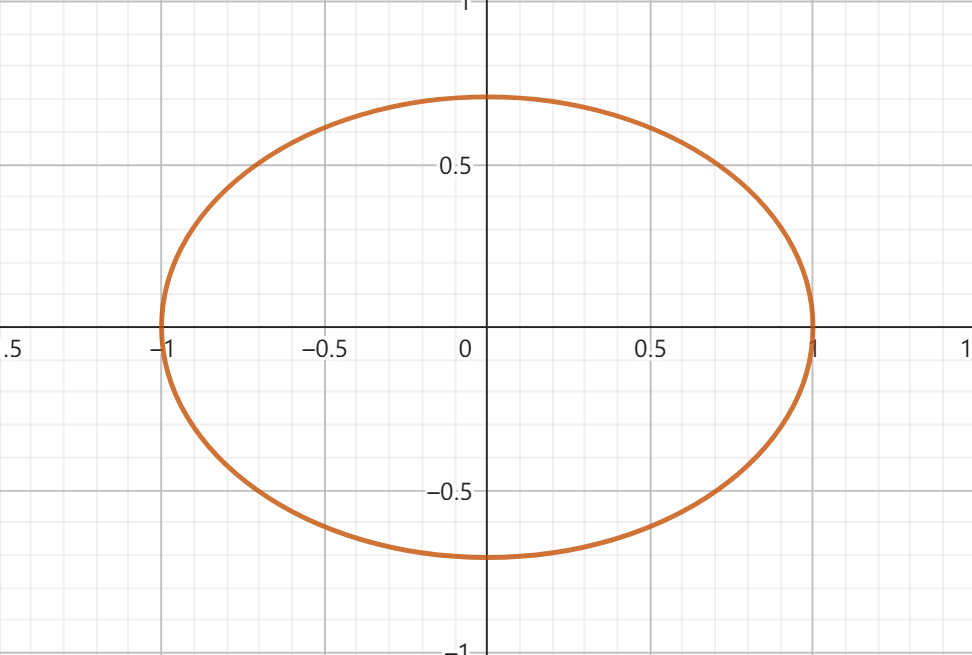
我们成功将一个斜椭圆转换为了正椭圆,因此可以通过合同变换使得圆锥曲线的长轴和短轴与坐标轴共线,从而获得标准方程以简化研究。
但是我们发现刚才的变化有一个显著缺陷,也就是在转换之后,椭圆的形状改变了,这破坏了他原有的性质。
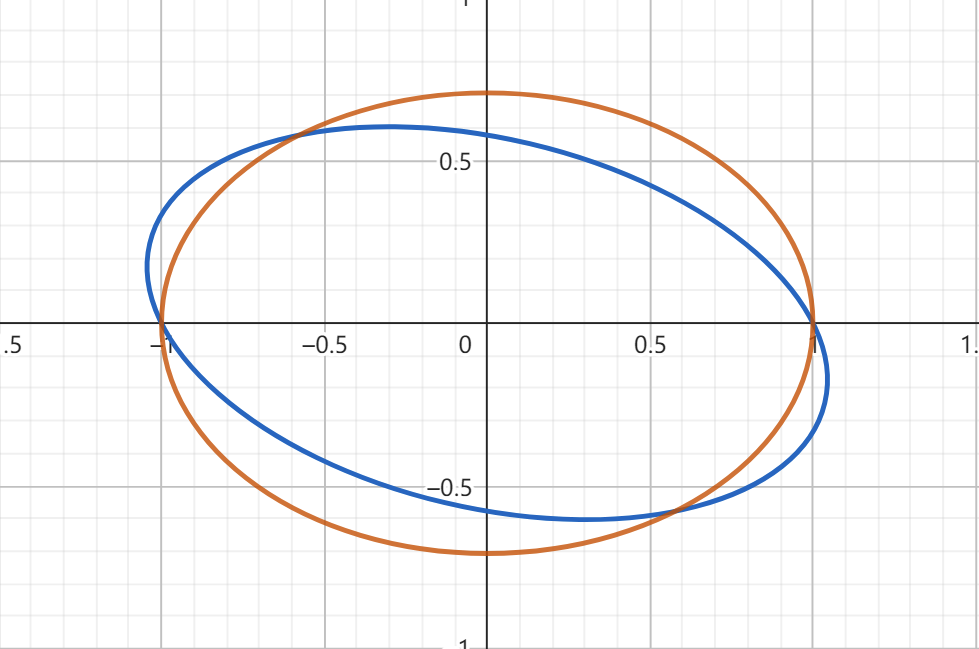
合同变换时,我们需要保证变换前后椭圆是全等状态,即椭圆上的每一个点都单纯发生旋转变换,我们需要从矩阵的角度去探讨这个问题。
设二次型 \(f = x^T A x\),可逆合同变换矩阵 \(Q\) 使得 \(U = Q^T A Q\) 和 \(f = y^T U y\) 成立,需要 \(U\) 是对角矩阵且变换前后任意一点到原点的距离不变,可以得出 \(\Vert x \Vert = \Vert y \Vert\) 即 \(x^T x = y^T y\),带入 \(x = Qy\) 有:
这要求 \(Q^T Q = E\),我们称满足这样的 \(Q\) 为正交矩阵。
因此我们想要维持原有二次型的性质,我们要求他的基变换矩阵必须要是正交矩阵。
正交矩阵的性质
因为 \(Q^T Q = E\) 且 \(\vert Q^T \vert = \vert Q \vert\),可以推出 \(\vert Q \vert^2 = 1\),故正交矩阵的行列式只能为 \(1\) 或 \(-1\) 。
更优秀的,因为 \(Q^{-1}Q = E\),所以 \(Q^{-1} = Q^T\),正交矩阵的逆矩阵与转置矩阵相等。
将 \(Q\) 分块为 \(n\) 组列向量 \(Q = (q_1, \ldots, q_n)\),我们有:
这意味正交矩阵任意一列(行)向量都是单位向量且两两正交,全体列(行)向量可以作为一组单位正交基向量组。
二次型 \(f = x^T A x\) 中,使用正交矩阵 \(Q\) 对实对称矩阵 \(A\) 经过合同变换化为对角阵 \(U\),则有:
由于实对称矩阵 \(A\) 到他的特征值矩阵 \(U\) 是合同相似的,它必有正交的特征向量组,我们很多时候不需要求出可逆的变换矩阵 \(Q\),因为这个矩阵是客观存在的。
通过这种方式化成的标准型不仅保留原先二次型的类型,还使得二次型得以全等地变换,并保持各个方向的伸缩因子不变,更重要的是建立起了二次型合同对角化和实对称矩阵的相似对角化的关系,这样就可以使用对实对称矩阵相似对角化的方法题来解决化二次型为标准型的问题。
与曲线的关系
不妨考虑上面 \(x_1^2 + 2x_1x_2 + 3x_2 = 1\) 的性质,他的二次型可以表示为:
我们可以求解它的特征值:
所以经过合同变换后的二次型变为:
也就是 \((2 - \sqrt{2})y_1^2 + (2 + \sqrt{2})y_2^2 = 1\),我们现在可以直观地求出这个椭圆的长短轴和面积,无疑简化了我们的运算。
更一般的,由于 \(ax_1^2 + bx_1x_2 + cx_2^2 = 1\) 可以转换为 \(\lambda_1y_1^2 + \lambda_2y_2^2 = 1\),由于两个二次型矩阵的是相似的,我们可以得到:
记 \(\Delta = b^2 - 4ac\),我们甚至可以直接看出二次曲线的类型:
-
当 \(a + c > 0\) 且 \(\Delta < 0\) 时,\(\lambda\) 均为正数,对应曲线为椭圆。
-
当 \(a + c < 0\) 且 \(\Delta < 0\) 时,对应曲线在 \(f = 1\) 时无意义。
-
当 \(\Delta > 0\) 时,\(\lambda\) 一正一负,对应曲线为双曲线。
-
当 \(\Delta = 0\),即 \(\vert A \vert = 0\) 时,必有特征值为 \(0\),所以原二次型可写作 \((a + c)y_1^2 = 1\),为两条平行直线。
更平凡的,如果为三元二次型,我们也能得到类似的结论,我们列出一个表格,但不再继续说明。
| 特征值 | 曲面类型 |
|---|---|
| 三正 | 椭球面 |
| 三负 | 无意义 |
| 两正一负 | 单叶单曲面 |
| 两负一正 | 双叶双曲面 |
| 两正一零 | 椭圆柱面 |
| 两负一零 | 无意义 |
| 一正一负一零 | 双曲柱面 |
| 一非零,两零 | 两平面平行 |


 浙公网安备 33010602011771号
浙公网安备 33010602011771号