NZOJ 模拟赛5

T1 逃离遗迹

根据外星人的回信，在遗迹中有分布着三样道具。当三样道具都拿走后，遗迹就很快自动毁灭，所以必须要在最短时间内离开。遗迹可以看作是由N个房间(编号1..N)和N-1条长度不等通道所组成，并且任意两个房间之间有且只有一条路可以相互到达。现在我们的队员已经在编号为A,B,C的房间内拿到道具，并且准备撤退。由于只有一架直升机，所以只能在一个房间上停留。现在请你决定将直升机停在哪一个房间之上，能够使三人到达该房间的距离之和最短。

考虑最短路模型，对 \(A, ~ B, ~ C\) 三个点分别作为源点跑一次最短路，扫一遍所有的点，找到 \(dist[A] + dist[B] + dist[C]\) 最小的点即可。

T2 遗址

很久很久以前有一座寺庙，从上往下看寺庙的形状正好是一个正方形，在4个角上竖立着圆柱搭建而成。现在圆柱都倒塌了，只在地上留下圆形的痕迹，可是现在地上有很多这样的痕迹，专家说一定是最大的那个。
写一个程序，给出圆柱的坐标，找出由4个圆柱构成的最大的正方形，因为这就是寺庙的位置，要求计算出最大的面积。注意正方形的边不一定平行于坐标轴。
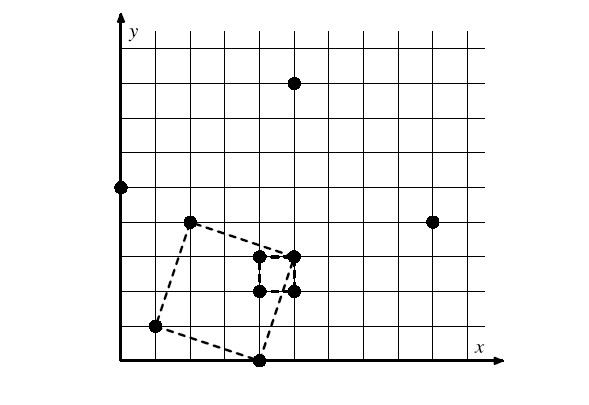
例如下图有10根柱子，其中(4,2),(5,2),(5,3),(4,3)可以形成一个正方形，(1,1),(4,0),(5,3),(2,4)也可以，后者是其中最大的，面积为10。

考虑枚举正方形对角线上两点 \((x_1, ~ y_1), ~ (x_2, ~ y_2)\)，可以轻松计算出另外两点的坐标，判断另外两点是否存在即可，如果存在，则更新我们的答案，初始化答案为 \(-1\)，如果结果为 \(-1\) 则不存在正方形。

T3 迷之阶梯

在经过地球防卫小队的数学家连续多日的工作之后，外星人发的密码终于得以破解。它告诉我们在地球某一处的古老遗迹中，存在有对抗这次灾难的秘密道具。防卫小队立刻派出了一个直升机小分队，迅速感到了这处遗迹。要进入遗迹，需要通过一段迷之阶梯。登上阶梯必须要按照它要求方法，否则就无法登上阶梯。它要求的方法有以下三个限制：

1. 如果下一步阶梯的高度只比当前阶梯高1，则可以直接登上。

2. 除了第一步阶梯外，都可以从当前阶梯退到前一步阶梯。

3. 当你连续退下k后，你可以一次跳上不超过当前阶梯高度2^k的阶梯。比如说你现在位于第j步阶梯，并且是从第j + k步阶梯退下来的。那么你可以跳到高度不超过当前阶梯高度 + 2^k的任何一步阶梯。跳跃这一次只算一次移动。

开始时我们在第1步阶梯。由于时间紧迫，我们需要用最少的移动次数登上迷之阶梯。请你计算出最少的移动步数。

考虑动规，不妨设 \(dp[i]\) 表示到达第 \(i\) 级别阶梯即 \(h[i]\) 高度时的最少步数，我们模拟每个后退的过程，记录后退了 \(k\) 步，对于 \(i\) 以后的阶梯 \(t\) 只要满足 \(h[t] - h[i - k] <= (1 << k)\) 即可转移 \(dp[t] = min(dp[t], dp[i - 1] + k + 1)\)，我们可以枚举 \(t\) 和 \(k\) 完成转移，这样是 \(O(n^3)\) 的，不过足以通过此题了，此题还有 \(O(n^2)\) 的做法，欢迎同学对代码改进。

参考代码

#include<bits/stdc++.h>
using namespace std;
const int N = 210;
int n, h[N], dp[N];

int main()
{
	cin >> n;
	memset(dp, 0x3f, sizeof dp), dp[1] = 0;
	for (int i = 1; i <= n; i ++ ) cin >> h[i];
	for (int i = 2; i <= n; i ++ )
		for (int j = i - 1, k = 0; j; j -- , k ++ )
			for (int t = i; t <= n; t ++ )
				if (k >= 31 || h[t] - h[j] <= (1 << k))
					dp[t] = min(dp[t], dp[i - 1] + k + 1);
	cout << (dp[n] == 0x3f3f3f3f ? -1 : dp[n]);
	return 0;
}

T4 买票

周末Ztc想去剧场看演出,但他没有票。这时,救世主Wzj出现了,他慷慨地愿意卖给Ztc一些票。
Wzj手上共有n张票,但每张票的费用都不一样，贪心的ztc想要得到尽可能多的票，但又想花费最少,慷慨的wzj愿意给连续的m张票。
Ztc希望你能帮助他在花钱范围内取得最大的票数。

双指针板题，考虑扩大右指针后，左指针右移使得区间和小于上界，对区间和取 \(max\) 即可。