IMO2025 Problem 3

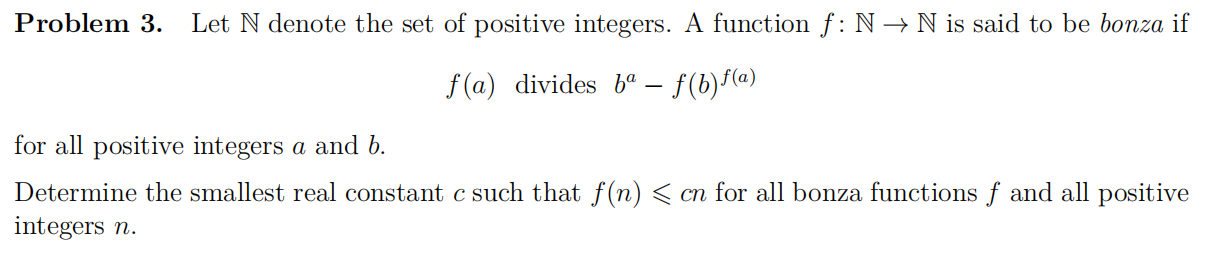
\(f(x) = x\) 或 \(f(x) \equiv 1\) 显然成立，我们考虑是否存在其他的函数。

注意到 \(a = b\) 时，原条件等价于：

\[a^a \equiv f(a)^{f(a)} \equiv 0\pmod{f(a)} \]

故 \(f(a) \mid a^a\)。

设 \(a = p, \, b = q\) 为两不同素数，因为 \(f(a) \mid a^a\)，可以推出 \(p\varphi(f(p)) = f(p)\) 或 \(f(p) = 1\)，那么原式等价于：

\[q^{p} - f(q)^{f(p)} \equiv q^{p} - 1 \equiv 0 \pmod{f(p)} \]

若 \(p \mid f(p)\)，则有：

\[q^{p} - 1 \equiv q - 1 \not\equiv 0 \pmod{p} \]

当且仅当 \(p = 2\) 时成立，否则显然不合法，故 \(p \neq 2\) 时 \(f(p) = 1\)。

• 若此时 \(f(2) = 1\)，则考虑如下证明：

  设 \(b = p\) 为某素数，\(a\) 为某合数，则：

  \[a^p \equiv 1 \pmod{f(a)} \]

  若 \(f(a) \neq 1\)，则 \(a \mid f(a)\)，对 \(a\) 的所有素数幂 \(q_i^{k_i}\) 检查可以得到：

  \[a^{p} \equiv 0 \pmod{q_i^{k_i}} \]

  故当且仅当 \(f(a) \equiv 1\) 时成立。

  综上 \(f(x) = 1\) 恒成立。

为了避免重复我们考虑 \(p = 2\) 时 \(f(p) = 2\) 或 \(f(p) = 4\)，可以验证，这两种取值在上述条件下合法。

接下来考虑取 \(a\) 为任意正整数，\(b = p\) 为任意奇素数，有：

\[p^{a} - f(p)^{f(a)} \equiv p^a - 1 \equiv 0 \pmod{f(a)} \]

因此 \(f(a) \mid (p^a - 1)\) 也即 \(p \nmid f(a)\)，否则 \(p \mid (p^a - 1)\) 显然不合法，这意味着 \(f(a) = 2^{k}, \, k \in \mathbb{N}\)。

此时我们取 \(a\) 为任意正整数，\(b = 3\)，由 \(f(3) = 1\) 有：

\[f(a) \mid 3^a - 1 \]

由于 \(2 \mid (3 - 1)\) 且 \((2, \, 3) = 1\)，根据升幂引理可知：

\[\begin{aligned}\nu_2(3^a - 1) = \nu_2(3^2 - 1^2) + \nu_2(a) - 1 = \nu_2(a) + 2\end{aligned} \]

也即 \(\nu_2(f(a)) \le \nu_2(a) + 2\) 或写作 \(k \le \nu_2(a) + 2\)。

考虑设函数为：

\[f(x) = \begin{cases}2~\text{or}~4, & x = 2 \\ 2^{\nu_2(x) + 2}, & x \ge 4 \wedge 2 \mid x \\ 1, & \text{otherwise}\end{cases} \]

可以验证上述函数满足条件，且可得出此时的 \(c = 4\)，我们可以证明 \(c = 4\) 是一个最小值：

不妨设 \([x]\) 表示 \(x\) 去除 \(2\) 因子的剩余因数，即 \(2^{\nu_2(x)}[x] = x\)，有：

\[f(a) \le 2^{\nu_2(a) + 2} = 2^{\nu_2(a)} \cdot 4 \le 2^{\nu_2(a)}[a] \cdot 4 = 4a \]

因此 \(c_{\max} \le 4\)，\(c = 4\) 的构造已给出，综上 \(c = 4\)。