DP 优化专题

常见思路：

• 减少状态量：即优化状态表示（状压、滚动数组等）。

• 加速决策过程：二分、数据结构等。

• 缩小决策范围：单调队列/栈、斜率优化、四边形不等式优化等。

• 技巧性优化：前缀和等。

本文主要针对第三点展开讲解。

斜率优化

斜率优化的题目通常具有以下特征：

• 转移方程中含有乘积式，通常用平方得到。

• 有一些具有单调性的东西，如前缀和等。

尤其是第一点，是斜率优化题目极为明显的特征。

接下来，我们从一个经典题目入手，详细讲解它的原理逻辑。

P3195

很容易设计朴素 dp。

令 \(dp_i\) 表示压缩前 \(i\) 个玩具所需要的最小代价。

答案：\(dp_n\)，初始：\(dp_0=0\)。

转移：考虑对于每个 \(i\) 枚举 \(last\)，尝试将 \(last+1 \sim i\) 都放入一个容器，则 \(dp_i=dp_{last}+(i-last-1+\sum^i_{j=last} C_j-L)^2\)，其中 \(\sum\) 可以前缀和维护。

这样做的时间复杂度 \(\mathcal{O}(n^2)\)，无法接受。

注意到，\(dp_{last}\) 加上的东西是个乘积式，并且前缀和具有单调性，于是考虑斜率优化。

钦定 \(j,k\) 满足 \(k<j\)，且以 \(j\) 作为决策点比 \(k\) 更优。则有（以下令前缀和数组为 \(s_i\)）：

\[dp_j+(i-j-1+s_i-s_j-L)^2 \le dp_k+(i-k-1+s_i-s_k-L)^2 \]

不妨设 \(h_{i,j}=i-j-1+s_i-s_j\)，则有：

\[dp_j+(h_{i,j}-L)^2 \le dp_k+(h_{i,k}-L)^2\\ dp_j+h_{i,j}^2+L^2-2h_{i,j}L \le dp_k+h_{i,k}^2+L^2-2h_{i,k}L\\ dp_j+h_{i,j}^2-2h_{i,j}L \le dp_k+h_{i,k}^2-2h_{i,k}L \]

不妨再设 \(g_i=i+s_i-1,w_j=s_j+j\)，则有：

\[dp_j+(g_i-w_j)^2-2(g_i-w_j)L \le dp_k+(g_i-w_k)^2-2(g_i-w_k)L\\ dp_j+g_i^2+w_j^2-2g_iw_j-2g_iL+2w_jL \le dp_k+g_i^2+w_k^2-2g_iw_k-2g_iL+2w_kL\\ dp_j+w_j^2-2g_iw_j+2w_jL \le dp_k+w_k^2-2g_iw_k+2w_kL\\ \]

把含有 \(g_i\) 的项放到一边，其余的放到另一边，得到：

\[(dp_j+w_j^2+2w_jL)-(dp_k+w_k^2+2w_kL) \le 2g_i(w_j-w_k)\\ \dfrac{(dp_j+w_j^2+2w_jL)-(dp_k+w_k^2+2w_kL)}{w_j-w_k} \le 2g_i \]

实际上，\(g_i=w_i-1\)，于是整理得：

\[\dfrac{(dp_j+w_j^2)-(dp_k+w_k^2)+2L(w_j-w_k)}{w_j-w_k} \le 2(w_i-1)\\ \dfrac{(dp_j+w_j^2)-(dp_k+w_k^2)}{w_j-w_k}+2L \le 2(w_i-1)\\ \dfrac{(dp_j+w_j^2)-(dp_k+w_k^2)}{w_j-w_k} \le 2(w_i-L-1) \]

换元，令 \(y_i=dp_i+w_i^2,x_i=w_i\)，得：

\[\dfrac{y_j-y_k}{x_j-x_k} \le 2(w_i-L-1) \]

左边这个式子长得很像直线的斜率，故称此方法为斜率优化（Convex Hull Trick）。

这个式子表明，在当前 \(i\) 的前提下，当一对 \(j,k\) 满足 \(k<j\) 且满足上式时，\(j\) 一定更优。

那么，\(i+1\) 时是否同样成立？因为前缀和单调不减，所以 \(2(w_i-L-1)\) 同样单调不减，因此 \(i+1\) 时显然成立。

于是，我们可以维护一个单调队列，每次剔除不优的队头，然后从队头转移。在插入 \(i\) 进入队列时，我希望斜率越来越大（因为不等式右边在变大），所以当队尾和次队尾的斜率比队尾和 \(i\) 的斜率小，我就弹出队尾（总不能弹出 \(i\) 吧，这样的话就不会有新的决策点进入了）。

由于每个决策点至多进队/出队一次，因此时间复杂度 \(\mathcal{O}(n)\)。

实现

#include<bits/stdc++.h>
#define int long long
using namespace std;

const int N=5e5+5;
int n,m;
int dp[N],sum[N],q[N],h[N];

int up(int j,int k){
	return (dp[j]+h[j]*h[j])-(dp[k]+h[k]*h[k]);
}
int down(int j,int k){
	return h[j]-h[k];
}
void sol(){
	cin>>n>>m;
	for(int i=1;i<=n;i++)
		cin>>sum[i],sum[i]+=sum[i-1];
	int l=1,r=0;
	q[++r]=0;
	for(int i=1;i<=n;i++){
		h[i]=sum[i]+i;
		for(;l<r&&up(q[l+1],q[l])<=2*(h[i]-m-1)*down(q[l+1],q[l]);l++);
		dp[i]=dp[q[l]]+(sum[i]-sum[q[l]]+i-q[l]-1-m)*(sum[i]-sum[q[l]]+i-q[l]-1-m);
		for(;l<r&&up(i,q[r])*down(q[r],q[r-1])<=up(q[r],q[r-1])*down(i,q[r]);r--);
		q[++r]=i;
	}
	cout<<dp[n]<<'\n';
} 

signed main(){
	ios::sync_with_stdio(0);
	cin.tie(0);
	sol();
	return 0;
}

事实上，因为队列中的斜率递增，所以我们维护的决策点集合相当于一个下凸壳。如图：

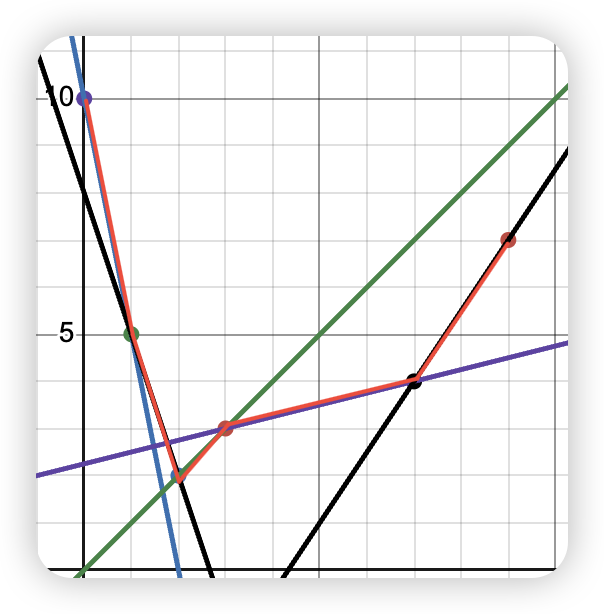
（红线标出的是下凸壳，\(\texttt{x-axis}\) 为 \(w_i\)，\(\texttt{y-axis}\) 为 \(dp_i+w_i^2\)）

这也是为什么斜率优化的英文名是「Convex Hull Trick」，即所谓「凸包技巧」。

P2900

诈骗题。

显然，有很多土地是无效的，具体而言，是那些长和宽都比不过别人的。

容易想到按照长或者宽降序排列土地，这里以宽为例。我们发现，当剔除了那些无效土地之后，对于一段连续的区间，其左端点的宽最大，右端点的长最大，中间的对于答案没有贡献。这样，选一段连续区间一定最优，于是我们就可以进行 dp 了。推一下式子可以发现能斜率优化，然后就做完了。

实现

#include <cstdio>
#include <iostream>
#include <algorithm>
#include <cstring>
#include <string>
#include <stdlib.h>
#include <vector>
#include <queue>
#include <cmath>
#include <stack>
#include <map>
#include <set>
#define int long long
using namespace std;

const int N=5e4+5;
int n;
int dp[N],q[N];
pair<int,int> a[N];

int up(int j,int k){
	return dp[j]-dp[k];
}
int down(int j,int k){
	return a[k+1].first-a[j+1].first;
}
bool cmp(pair<int,int> &x,pair<int,int> &y){
	return x.first==y.first?x.second>y.second:x.first>y.first;
}
void sol(){
	cin>>n;
	for(int i=1;i<=n;i++)
		cin>>a[i].first>>a[i].second;
	sort(a+1,a+n+1,cmp);
	int tot=0;
	for(int i=1;i<=n;i++)
		if(a[tot].second<a[i].second)
			a[++tot]=a[i];
	int l=1,r=0;
	q[++r]=0;
	for(int i=1;i<=tot;i++){
		for(;l<r&&up(q[l+1],q[l])<=a[i].second*down(q[l+1],q[l]);l++);
		dp[i]=dp[q[l]]+a[q[l]+1].first*a[i].second;
		for(;l<r&&up(i,q[r])*down(q[r],q[r-1])<=up(q[r],q[r-1])*down(i,q[r]);r--);
		q[++r]=i;
	}
	cout<<dp[tot]<<'\n';
} 

signed main(){
	ios::sync_with_stdio(0);
	cin.tie(0);
	sol();
	return 0;
}

总结：dp 考虑连续区间、剔除无效状态。

单调队列优化

从本质上看，斜率优化也是一种单调队列优化

单调队列优化的题，一般具有以下特征：

• 决策点有上界和下界，且都具有单调性（说白了就是能滑动窗口）。

我们对着例题讲解。

P2627

很容易想出一个朴素 dp。

令 \(dp_{i,0/1}\) 表示前 \(i\) 头牛且第 \(i\) 头牛选 / 不选的最大效率值。

初始 \(dp_{0,0}=0\)，答案 \(\max(dp_{n,0},dp_{n,1})\)。

转移 \(dp_{i,0}=\max(dp_{i-1,0},dp_{i-1,1})\)；\(dp_{i,1}=\max\{dp_{j,0}+s_i-s_j\}\)，其中 \(s_i = \sum^n_{i=1} E_i\)，\(\red{j \in [i-k,i-1]}\)。

这样做时间复杂度 \(\mathcal{O}(n^2)\)，无法接受。

观察红色部分，它表明 \(j\) 具有上下界，并且 \(i-k,i-1\) 显然单调递增，符合单调队列优化的特征，考虑单调队列优化之。

至于怎么实现，当然是队头框住区间，然后队尾处理最优化问题（比我大还比我菜就可以 out 了）即可。

实现

#include<bits/stdc++.h>
#define int long long
using namespace std;

const int N=1e6+5;
int n,k;
int sum[N],dp[N][2],q[N];

signed main(){
	ios::sync_with_stdio(0);
	cin.tie(0);
	cin>>n>>k;
	for(int i=1;i<=n;i++)
		cin>>sum[i],sum[i]+=sum[i-1];
	int l=1,r=1;
	memset(dp,0xcf,sizeof dp);
	dp[0][0]=0;
	for(int i=1;i<=n;i++){
		for(;l<=r&&q[l]<i-k;l++);
		dp[i][0]=max(dp[i-1][0],dp[i-1][1]);
		dp[i][1]=dp[q[l]][0]+sum[i]-sum[q[l]];
		for(;l<=r&&dp[q[r]][0]-sum[q[r]]<=dp[i][0]-sum[i];r--);
		q[++r]=i;
	}
	cout<<max(dp[n][0],dp[n][1]);
	return 0;
}

总结：对于只有一边有界限（不是 \(i-1,i+1\) 这种）的决策点区间，总是左端点框住区间，右端点处理最优化问题。

P1725

这个题，它决策点的集合是 \([i-R,i-L]\)，于是我们实现的时候插入 \(i\) 的时候不能直接插，而是要在 \(i+L\) 的时候插就可以了。

实现

#include<bits/stdc++.h>
#define int long long
using namespace std;

const int N=2e5+5;
int n,L,R;
int a[N],dp[N],q[N];

signed main(){
	ios::sync_with_stdio(0);
	cin.tie(0);
	cin>>n>>L>>R;
	for(int i=0;i<=n;i++)
		cin>>a[i];
	int l=1,r=1;
	memset(dp,0xcf,sizeof dp);
	dp[0]=0;
	int ans=-1e9;
	for(int i=L;i<=n;i++){
		for(;l<=r&&dp[q[r]]<=dp[i-L];r--);
		q[++r]=i-L;
		for(;l<=r&&q[l]+R<i;l++);
		dp[i]=dp[q[l]]+a[i];
		if(i+R>n)
			ans=max(ans,dp[i]);
	}
	cout<<ans;
	return 0;
}

总结：两边都有界限的，要注意插入时机。

P3089

考虑朴素 dp。

令 \(dp_{i,j}\) 表示当前点为 \(i\) 且 \(j \to i\) 的最大得分。

初始 \(dp_{0,0}=0\)，答案 \(\max\{dp_{i,j}\}\)。

转移 \(dp_{i,j}=\max\{dp_{j,k}\}+p_i\)，其中 \(j,k\) 满足 \(a_i-a_j \ge a_j-a_k\)。

注意需要将目标点按照坐标从小到大排序，并做正反两遍 dp。

时间复杂度 \(\mathcal{O}(n^3)\)，无法接受。

考虑优化状态表示：观察如下式子。

\[dp_{i-1,j}=\max\{dp_{j,k}\}+p_{i-1} \]

容易发现，\(dp_i=dp_{i-1}-p_{i-1}+p_i\)，这样不就少了一维 \(k\) 吗？

没有这么简单，需要注意以下两点：

• 从 \(dp_{i-1}\) 到 \(dp_i\)，\(k\) 的限制是会变化的，所以要先拓展出新的 \(dp_{j,k}\) 取完 \(\max\) 之后才能直接像上面一样转移。

• 因为我们从 \(dp_{i-1}\) 转移到 \(dp_i\)，所以要先枚举 \(j\)，再枚举 \(i\)。

实现

#include <cstdio>
#include <iostream>
#include <algorithm>
#include <cstring>
#include <string>
#include <stdlib.h>
#include <vector>
#include <queue>
#include <cmath>
#include <stack>
#include <map>
#include <set>
#define int long long
using namespace std;

const int N=1e3+5;
int n;
int dp[N][N];
struct A{
	int x,p;
}a[N];

bool cmp(A &u,A &v){
	return u.x<v.x;
}

signed main(){
	ios::sync_with_stdio(0);
	cin.tie(0);
	cin>>n;
	for(int i=1;i<=n;i++)
		cin>>a[i].x>>a[i].p;
	sort(a+1,a+n+1,cmp);
	int ans=0;
	memset(dp,0xcf,sizeof dp);
	dp[0][0]=0;
	for(int j=1;j<=n;j++){
		dp[j][j]=a[j].p;
		ans=max(ans,dp[j][j]);
		for(int i=j+1,cur=j+1;i<=n;i++){
			dp[i][j]=dp[i-1][j]-a[i-1].p;
			while(cur>1&&a[j].x-a[cur-1].x<=a[i].x-a[j].x)
				dp[i][j]=max(dp[i][j],dp[j][--cur]);
			dp[i][j]+=a[i].p;
			ans=max(ans,dp[i][j]);
		}
	}
	for(int j=n;j>=1;j--){
		dp[j][j]=a[j].p;
		ans=max(ans,dp[j][j]);
		for(int i=j-1,cur=j-1;i>=1;i--){
			dp[i][j]=dp[i+1][j]-a[i+1].p;
			while(cur<n&&a[cur+1].x-a[j].x<=a[j].x-a[i].x)
				dp[i][j]=max(dp[i][j],dp[j][++cur]);
			dp[i][j]+=a[i].p;
			ans=max(ans,dp[i][j]);
		}
	}
	cout<<ans;
	return 0;
}

总结：继承技巧、调整枚举顺序的技巧。

结语

• dp 考虑连续区间、剔除无效状态。

• 继承技巧、调整枚举顺序的技巧。

• 单调队列优化有无界限的情况处理。

以上。