可持久化数据结构
一种比较高级的科技。
我们以往学习的数据结构都具有即时性,即进行修改之后无法回溯。
当我们想要了解某次修改后的状态时(你可以理解为「回档」),就需要额外维护数据结构的历史版本。
从朴素的角度考虑,我们完全可以开 \(n\) 个数据结构进行维护。但这样的空间复杂度往往过高,无法承受。
于是,可持久化数据结构最核心的思想即为「共用」(事实上,这也是一些运用可持久化数据结构题目中的明显提示)。具体而言:
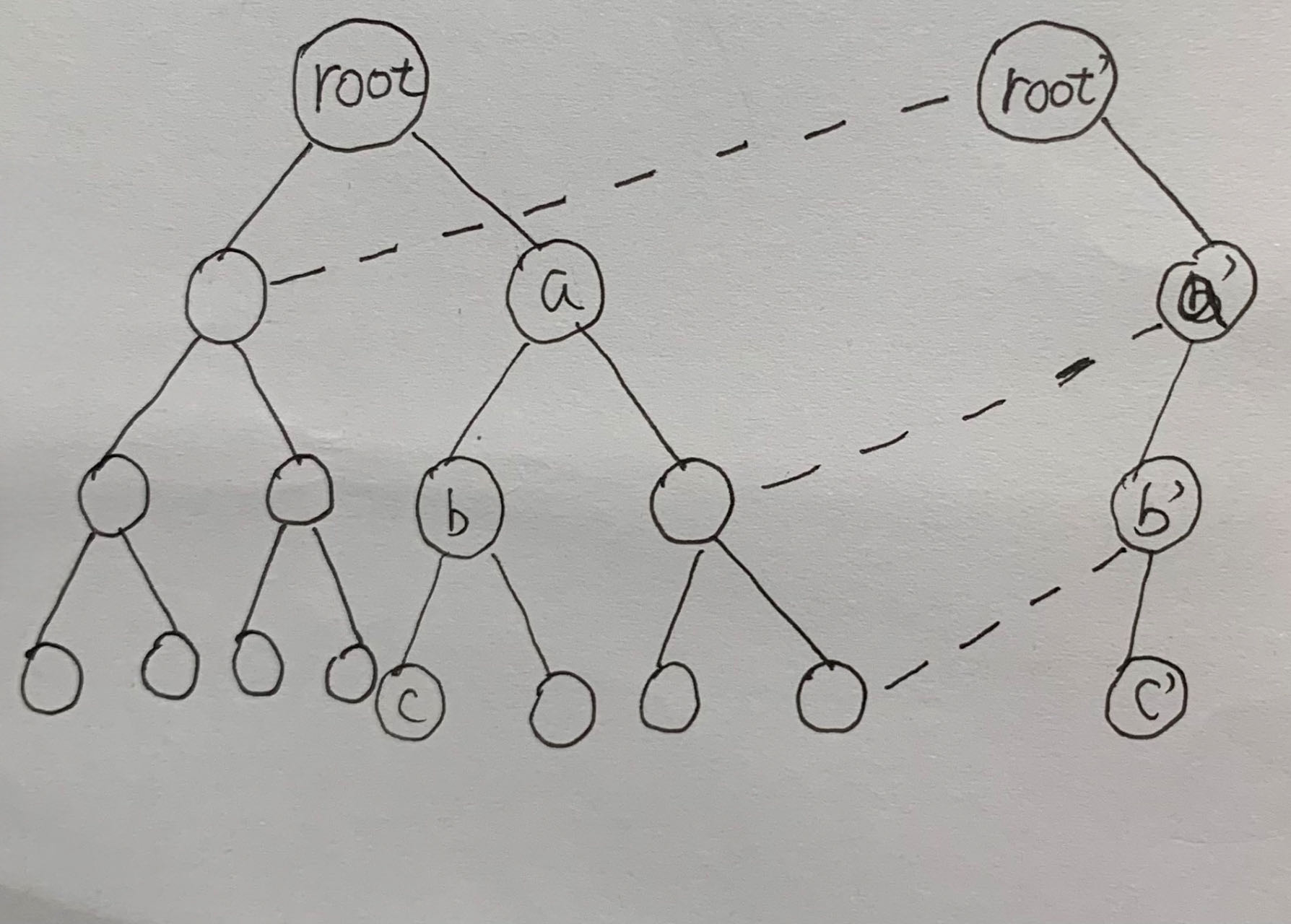
在这张图中,我们以线段树为例,构建了一棵以 \(root\) 为根的线段树。当我们尝试对于 \(c\) 这个叶子节点进行修改时,因为 \(root-a-b-c\) 这条路径上的点都需要修改,所以我们仅需复制一份路径 \(root'-a'-b'-c'\),并保持原树的形态(即 \(a'\) 与 \(a\) 的左右儿子不变)。事实上,新生成的是一个森林,但对于线段树而言,这并无大碍。
以上便是可持久化数据结构的基本逻辑。
补充:容易发现,主席树是一种类似于前缀和的数据结构,所以什么前缀和、差分之类的东西都可以往上面套。
P3919
模板。
实现
#include<bits/stdc++.h>
#define int long long
using namespace std;
const int N=1e6+5;
int n,m,tot;
int a[N],root[N];
struct TREE{
int lt,rt,val;
}tree[N*24]; //注意24倍空间
int build(int lt,int rt){ //建树
int p=++tot;
if(lt==rt){
tree[p].val=a[lt];
return p;
}
int mid=(lt+rt)>>1;
tree[p].lt=build(lt,mid);
tree[p].rt=build(mid+1,rt);
return p;
}
int upd(int cur,int lt,int rt,int pos,int val){
int p=++tot; //新建一个节点
tree[p]=tree[cur]; //保持原树形态
if(lt==rt){
tree[p].val=val; //修改
return p;
}
int mid=(lt+rt)>>1;
if(pos<=mid) //必须这样写,不能两棵子树都修改
tree[p].lt=upd(tree[cur].lt,lt,mid,pos,val); //连接新的左子树
else
tree[p].rt=upd(tree[cur].rt,mid+1,rt,pos,val); //或者连接新的右子树
return p;
}
int qry(int cur,int lt,int rt,int pos){
if(lt==rt)
return tree[cur].val;
int mid=(lt+rt)>>1;
if(pos<=mid)
return qry(tree[cur].lt,lt,mid,pos);
else
return qry(tree[cur].rt,mid+1,rt,pos);
}
signed main(){
ios::sync_with_stdio(0);
cin.tie(0);
cin>>n>>m;
for(int i=1;i<=n;i++)
cin>>a[i];
root[0]=build(1,n); //初始版本
for(int i=1;i<=m;i++){
int v,op,pos,val;
cin>>v>>op>>pos;
if(op==1)
cin>>val,root[i]=upd(root[v],1,n,pos,val); //新建一个版本
else
cout<<qry(root[v],1,n,pos)<<'\n',root[i]=root[v]; //注意查询也需要新建(依题意)
}
return 0;
}
P3834
事实上,这才是可持久化线段树的经典应用。
首先,我们考虑静态整体第 \(k\) 大如何使用线段树解决。
我们开一棵权值线段树,维护值域区间。同时,我们统计对于每个值,它出现的次数 \(cnt\)。对于线段树上的一个区间 \([l,r]\),若 \([l,mid]\) 的 \(\sum cnt > k\),说明要去右区间寻找答案,否则去左区间。
回归本题,现在加上了区间的限制,如何解决?
我们考虑刻画这个约束条件。运用前缀和的思想,我们直接将区间 \([l,r]\) 划分为 \([1,r]-[1,l-1]\),线段树维护相同的信息。这样,我们便可以将每一个区间 \([1,x]\) 看作一个历史版本,然后用两个版本作差的方法得到 \(\sum cnt\) 即可直接做了。
总结:将区间看作历史版本。
实现
#include<bits/stdc++.h>
#define int long long
using namespace std;
const int N=2e5+5;
int n,m,tot;
int a[N],t[N],root[N];
struct TREE{
int lt,rt,sum;
}tree[N*24];
void pushup(int p){
tree[p].sum=tree[tree[p].lt].sum+tree[tree[p].rt].sum;
}
int build(int lt,int rt){
int p=++tot;
tree[p].sum=0;
if(lt==rt)
return p;
int mid=(lt+rt)>>1;
tree[p].lt=build(lt,mid);
tree[p].rt=build(mid+1,rt);
return p;
}
int upd(int cur,int lt,int rt,int pos,int val){
int p=++tot;
tree[p]=tree[cur];
if(lt==rt){
tree[p].sum+=val;
return p;
}
int mid=(lt+rt)>>1;
if(pos<=mid)
tree[p].lt=upd(tree[cur].lt,lt,mid,pos,val);
else
tree[p].rt=upd(tree[cur].rt,mid+1,rt,pos,val);
pushup(p);
return p;
}
int qry(int cur,int last,int lt,int rt,int pos){
if(lt==rt)
return lt;
int lsum=tree[tree[cur].lt].sum-tree[tree[last].lt].sum;
int mid=(lt+rt)>>1;
if(pos<=lsum)
return qry(tree[cur].lt,tree[last].lt,lt,mid,pos);
else
return qry(tree[cur].rt,tree[last].rt,mid+1,rt,pos-lsum);
}
signed main(){
ios::sync_with_stdio(0);
cin.tie(0);
cin>>n>>m;
for(int i=1;i<=n;i++)
cin>>a[i],t[i]=a[i];
sort(t+1,t+n+1);
int len=unique(t+1,t+n+1)-t-1;
root[0]=build(1,len);
for(int i=1;i<=n;i++){
a[i]=lower_bound(t+1,t+len+1,a[i])-t;
root[i]=upd(root[i-1],1,len,a[i],1);
}
for(int i=1,l,r,k;i<=m;i++){
cin>>l>>r>>k;
cout<<t[qry(root[r],root[l-1],1,len,k)]<<'\n';
}
return 0;
}
P2839
起初我想了个假做法,就是通过 \(a,b,c,d\) 确定中位数变动的区间,然后直接求区间 \(\max\) 即可。这个方法显然是错的,因为中位数不一定在这个区间里能全部取到。
回归正题。看到中位数考虑二分答案。
如何 check?这时我们需要对数组进行处理。对于一个答案 \(x\),将大于等于它的设为 \(1\),否则设为 \(-1\)。
容易发现,这样处理之后,若区间(即 \([a,b]\) 的最大后缀 + \([b+1,c-1]\) + \([c,d]\) 的最大前缀)和 \(\ge 0\) 则需要变大,否则需要变小。这样便完成了 check 的设计。
现在的问题在于时间复杂度过高。如何优化?可以发现瓶颈在于对数组的处理,容易想到对于每一个 \(x\) 开一棵线段树,但空间炸了。于是运用可持久化线段树,对于每一个 \(x\) 开一个历史版本即可。
总结:
-
看到中位数考虑二分答案。
-
对数组处理的思想。
-
运用可持久化的思想优化空间。
实现
#include <cstdio>
#include <iostream>
#include <algorithm>
#include <cstring>
#include <string>
#include <stdlib.h>
#include <vector>
#include <queue>
#include <cmath>
#include <stack>
#include <map>
#include <set>
#define int long long
using namespace std;
const int N=2e4+5;
int n,q,tot,len;
int a[N],t[N],root[N];
struct TREE{
int lt,rt,sum,pre,suf;
}tree[N<<6];
vector<int> num[N];
void pushup(int p){
tree[p].sum=tree[tree[p].lt].sum+tree[tree[p].rt].sum;
tree[p].pre=max(tree[tree[p].lt].pre,tree[tree[p].lt].sum+tree[tree[p].rt].pre);
tree[p].suf=max(tree[tree[p].rt].suf,tree[tree[p].rt].sum+tree[tree[p].lt].suf);
}
int build(int lt,int rt){
int p=++tot;
tree[p].sum=tree[p].pre=tree[p].suf=0;
if(lt==rt)
return p;
int mid=(lt+rt)>>1;
tree[p].lt=build(lt,mid);
tree[p].rt=build(mid+1,rt);
return p;
}
int upd(int cur,int lt,int rt,int pos,int val){
int p=++tot;
tree[p]=tree[cur];
if(lt==rt){
tree[p].sum=tree[p].pre=tree[p].suf=val;
return p;
}
int mid=(lt+rt)>>1;
if(pos<=mid)
tree[p].lt=upd(tree[cur].lt,lt,mid,pos,val);
else
tree[p].rt=upd(tree[cur].rt,mid+1,rt,pos,val);
pushup(p);
return p;
}
int qrysum(int cur,int lt,int rt,int ql,int qr){
if(lt>qr||rt<ql)
return 0;
if(ql<=lt&&rt<=qr)
return tree[cur].sum;
int mid=(lt+rt)>>1;
return qrysum(tree[cur].lt,lt,mid,ql,qr)+qrysum(tree[cur].rt,mid+1,rt,ql,qr);
}
int qrypre(int cur,int lt,int rt,int ql,int qr){
if(lt>qr||rt<ql)
return 0;
if(ql<=lt&&rt<=qr)
return tree[cur].pre;
int mid=(lt+rt)>>1;
return max(qrypre(tree[cur].lt,lt,mid,ql,qr),qrysum(tree[cur].lt,lt,mid,ql,qr)+qrypre(tree[cur].rt,mid+1,rt,ql,qr));
}
int qrysuf(int cur,int lt,int rt,int ql,int qr){
if(lt>qr||rt<ql)
return 0;
if(ql<=lt&&rt<=qr)
return tree[cur].suf;
int mid=(lt+rt)>>1;
return max(qrysum(tree[cur].rt,mid+1,rt,ql,qr)+qrysuf(tree[cur].lt,lt,mid,ql,qr),qrysuf(tree[cur].rt,mid+1,rt,ql,qr));
}
int fnd(int a,int b,int c,int d){
int l=0,r=len+1;
while(l+1<r){
int mid=(l+r)>>1;
if(qrysuf(root[mid],1,n,a,b-1)+qrysum(root[mid],1,n,b,c)+qrypre(root[mid],1,n,c+1,d)>=0)
l=mid;
else
r=mid;
}
return l;
}
signed main(){
ios::sync_with_stdio(0);
cin.tie(0);
cin>>n;
for(int i=1;i<=n;i++)
cin>>a[i],t[i]=a[i];
sort(t+1,t+n+1);
len=unique(t+1,t+n+1)-t-1;
for(int i=1;i<=n;i++){
a[i]=lower_bound(t+1,t+len+1,a[i])-t;
num[a[i]].push_back(i);
}
root[len+1]=build(1,n);
for(int i=1;i<=n;i++)
root[len+1]=upd(root[len+1],1,n,i,-1);
for(int i=len;i;i--){
root[i]=root[i+1];
for(int j:num[i])
root[i]=upd(root[i],1,n,j,1);
}
cin>>q;
int last=0;
for(int i=1,a,b,c,d;i<=q;i++){
cin>>a>>b>>c>>d;
a=(a+last)%n+1,b=(b+last)%n+1,c=(c+last)%n+1,d=(d+last)%n+1;
int q[]={a,b,c,d}; sort(q,q+4);
last=t[fnd(q[0],q[1],q[2],q[3])];
cout<<last<<'\n';
}
return 0;
}
CF1000F
显然可以莫队做,但时间复杂度过高。
对于一个元素 \(x\),令其上一次出现的位置为 \(last_x\),则对于一个区间 \([l,r]\),若\(\exist x \in [l,r],last_x<l\),说明 \([l,r]\) 中有只出现一次的数。
进一步的,若区间 \([l,r]\) 的所有元素中最小的那个 \(last_x<l\),才说明 \([l,r]\) 中有只出现一次的数。
于是,问题转化为求 \([l,r]\) 最小的 \(last_x\)。静态区间最值,可以使用可持久化线段树轻松解决。
注意,直接做是不行的,因为可能存在一个元素 \(x\),它出现了多次,但它第一次出现时的 \(last_x<l\),这样显然会导致判断错误。一个较简单的解决方案是,每遇到一个 \(x\),就将其 \(last_{last_x}\) 设为 \(\infty\),这样可以保证只留下最后一个 \(x\),从而保证答案的正确性。
总结:刻画答案和约束条件(转化成判断句)。
P3168
看到第 \(k\) 小和,显然主席树可以处理,对于时间轴上的每个时刻作为历史版本即可。
然后,我们发现区间和实际上是不好维护的。因为对于一个时刻,可能有许多任务区间能覆盖它,我如何知道这些区间对它的影响?这启发我们用一种方式去刻画任务区间,自然地,我们想到了差分。
具体而言,我们可以每到达一个时刻,令从它开始的任务区间的 \(l\) 能影响的所有区间(具体见代码) 都加上一个区间优先级,然后令从它结束的任务区间的 \(r+1\) 能影响的所有区间 都减去一个区间优先级。这样就可以很方便地维护区间和以及区间任务个数了。
然后这个题就做完了,注意几个代码中的细节即可。
总结:
-
见第 \(k\) 用主席树。
-
差分思想。
实现
#include <cstdio>
#include <iostream>
#include <algorithm>
#include <cstring>
#include <string>
#include <stdlib.h>
#include <vector>
#include <queue>
#include <cmath>
#include <stack>
#include <map>
#include <set>
#define int long long
using namespace std;
const int N=1e5+5;
int m,n,tot;
int p[N],root[N*48],t[N];
vector<int> L[N],R[N];
struct TREE{
int lt,rt,sum,cnt;
}tree[N*48];
int build(int lt,int rt){
int p=++tot;
tree[p].sum=tree[p].cnt=0;
if(lt==rt)
return p;
int mid=(lt+rt)>>1;
tree[p].lt=build(lt,mid);
tree[p].rt=build(mid+1,rt);
return p;
}
int upd(int cur,int lt,int rt,int pos,int val){
int p=++tot;
tree[p]=tree[cur];
tree[p].cnt+=val,tree[p].sum+=val*t[pos];
if(lt==rt)
return p;
int mid=(lt+rt)>>1;
if(pos<=mid)
tree[p].lt=upd(tree[cur].lt,lt,mid,pos,val);
else
tree[p].rt=upd(tree[cur].rt,mid+1,rt,pos,val);
return p;
}
int qry(int cur,int lt,int rt,int rnk){
if(lt==rt)
return tree[cur].sum/tree[cur].cnt*rnk; //细节 *rnk
int lcnt=tree[tree[cur].lt].cnt;
int mid=(lt+rt)>>1;
if(rnk<=lcnt)
return qry(tree[cur].lt,lt,mid,rnk);
return qry(tree[cur].rt,mid+1,rt,rnk-lcnt)+tree[tree[cur].lt].sum;
}
signed main(){
ios::sync_with_stdio(0);
cin.tie(0);
cin>>m>>n;
for(int i=1,s,e;i<=m;i++){
cin>>s>>e>>p[i],t[i]=p[i];
L[s].push_back(i);
R[e+1].push_back(i);
}
sort(t+1,t+m+1);
int len=unique(t+1,t+m+1)-t-1;
for(int i=1;i<=m;i++)
p[i]=lower_bound(t+1,t+len+1,p[i])-t;
root[0]=build(1,len);
for(int i=1;i<=n;i++){
root[i]=root[i-1];
for(int j:L[i])
root[i]=upd(root[i],1,len,p[j],1);
for(int j:R[i])
root[i]=upd(root[i],1,len,p[j],-1);
}
int last=1;
for(int i=1,x,a,b,c,k;i<=n;i++){
cin>>x>>a>>b>>c;
k=1+(a*last+b)%c;
if(k>tree[root[x]].cnt)
last=tree[root[x]].sum;
else
last=qry(root[x],1,len,k);
cout<<last<<'\n';
}
return 0;
}
CF1514D
这种众数题又不带修首先考虑主席树吧。
但我们目前还不知道怎么使用它,先放着。
考虑刻画一个合法区间的形态:若一个区间内有 \(tot\) 个「目标众数」(即严格大于区间长度一半向上取整的数),则必定有 \(tot-1\) 个非「目标众数」与之抵消。
接着,我们考虑划分的最优策略:显然对于每个众数分一个集合是最劣的,我们考虑两两进行合并。对于两个集合 \(tot_1,tot_1-1\),和 \(tot_2,tot_2-1\)(前者为「目标众数」,后者为非「目标众数」),它们合并之后为 \(tot_1+tot_2,tot_1+tot_2-2\),这并不符合要求。应该扔掉一个「目标众数」才行。这样,原先是两个集合,现在还是两个集合,这是最劣的情形。当「目标众数」很少时,还有可能更优。这便说明,合并两个集合不会更劣。
(这里补充一下,为什么每个集合都是形如 \(tot,tot-1\),这是因为,给每组「目标众数」都分配最少的非「目标众数」,则后面的其他「目标众数」将会有更多的选择,这是贪心的思想。)
得出上述结论后,考虑把所有集合合并到一块,即所有非「目标众数」均分布在一个集合内,这样必定是最不劣的。令「目标众数」有 \(tot\) 个,此时除了那个集合能够抵消的「目标众数」外,其余的必须自成一个集合,则答案即为
后面那部分是一定的,我们仅需求出 \(tot\) 即可,这就是主席树干的事情了,在线段树上二分即可(就是看左边的个数大于区间长一半就去左边,反之去右边,如果都不行就无解)。
实现:here.
总结:众数不带修考虑主席树、刻画答案、往最优化的方向思考。
CF893F
把深度看作历史版本,这样可以解决 \(k\) 的限制,然后上主席树求最小值即可。
需要注意的是,建树的时候不能在 dfs 里从父节点继承,而是同深度的都得加进去,所以要按照深度从小到大排序建。
具体见代码
#include <cstdio>
#include <iostream>
#include <algorithm>
#include <cstring>
#include <string>
#include <stdlib.h>
#include <vector>
#include <queue>
#include <cmath>
#include <stack>
#include <map>
#include <set>
#define int long long
using namespace std;
const int N=1e5+5;
const int INF=1e9;
int n,r,m,cnt,tot,lans,maxdep=-1e9;
int a[N],p[N],dep[N],siz[N],dfn[N],root[N];
vector<int> G[N];
struct TREE{
int lt,rt,mn;
}tree[N*32];
void pushup(int p){
tree[p].mn=min(tree[tree[p].lt].mn,tree[tree[p].rt].mn);
}
int upd(int p,int lt,int rt,int pos,int val){
int cur=++tot;
tree[cur]=tree[p];
if(lt==rt){
tree[cur].mn=val;
return cur;
}
int mid=(lt+rt)>>1;
if(pos<=mid)
tree[cur].lt=upd(tree[cur].lt,lt,mid,pos,val);
else
tree[cur].rt=upd(tree[cur].rt,mid+1,rt,pos,val);
pushup(cur);
return cur;
}
int qry(int p,int lt,int rt,int ql,int qr){
if(lt>qr||rt<ql)
return INF;
if(ql<=lt&&rt<=qr)
return tree[p].mn;
int mid=(lt+rt)>>1;
return min(qry(tree[p].lt,lt,mid,ql,qr),qry(tree[p].rt,mid+1,rt,ql,qr));
}
void dfs(int cur,int fa){
siz[cur]=1;
dep[cur]=dep[fa]+1;
dfn[cur]=++cnt;
maxdep=max(maxdep,dep[cur]);
for(int i:G[cur]){
if(i==fa)
continue;
dfs(i,cur);
siz[cur]+=siz[i];
}
}
bool cmp(int &x,int &y){
return dep[x]<dep[y];
}
signed main(){
ios::sync_with_stdio(0);
cin.tie(0);
tree->mn=INF;
cin>>n>>r;
for(int i=1;i<=n;i++)
cin>>a[i],p[i]=i;
for(int i=1,u,v;i<n;i++){
cin>>u>>v;
G[u].push_back(v);
G[v].push_back(u);
}
dfs(r,0);
sort(p+1,p+n+1,cmp);
for(int i=1;i<=n;i++)
root[dep[p[i]]]=upd(root[dep[p[i-1]]],1,n,dfn[p[i]],a[p[i]]);
cin>>m;
while(m--){
int x,k;
cin>>x>>k;
x=(x+lans)%n+1,k=(k+lans)%n;
lans=qry(root[min(dep[x]+k,maxdep)],1,n,dfn[x],dfn[x]+siz[x]-1);
cout<<lans<<'\n';
}
return 0;
}
总结:拓宽思维,万物皆可为历史版本。
结语
主席树有什么用?
-
优化空间
-
在单 \(\log\) 的复杂度内达成区间限制与值域限制的双重满足。
本文提到的技巧点?
-
万物皆可为历史版本
-
众数不带修考虑主席树
-
见第 \(k\) 用主席树
-
看到中位数考虑二分答案
以上。



 浙公网安备 33010602011771号
浙公网安备 33010602011771号