莫队

是一种由分块衍生出来的另一种暴力数据结构。

本质上是将询问离线，然后排序，使得左右端点移动的距离最小。

具体而言，就是先对序列分个块，然后对于两个询问，\(l\) 不在同一个块就按 \(l\) 排序，在同一个块就按 \(r\) 排序。

为什么这么排序呢？第一个规则很好理解，而第二个规则则是为了使左端点的移动距离不超过 \(\sqrt{n}\)。

时间复杂度反正是根号的。懒得分析了。

经验：

初始指针一般为 \(x=1,y=0\)。
效率很低？检查排序规则、用奇偶优化（即奇数块 \(r\) 从小到大排序，偶数块从大到小排序，这样减小一半常数）。

P3901

考虑莫队维护 \(cnt_i\) 表示 \(i\) 的出现次数，并维护 \(tot\) 表示当前区间的种类数，若对于一个询问区间满足 \(tot=r-l+1\) 则其中元素互不相同。

实现

#include<bits/stdc++.h>
using namespace std;

const int N=1e5+5;
int n,q,t,tot;
int a[N],ans[N],cnt[N];
struct Q{
	int l,r,id;
}qry[N]; 

bool cmp(Q &x,Q &y){
	if(x.l/t!=y.l/t)
		return x.l<y.l;
	return x.r<y.r;
}
void add(int x){
	cnt[a[x]]++;
	if(cnt[a[x]]==1)
		tot++;
}
void del(int x){
	cnt[a[x]]--;
	if(!cnt[a[x]])
		tot--;
}

signed main(){
	ios::sync_with_stdio(0);
	cin.tie(0);
	cin>>n>>q;
	t=sqrt(n);
	for(int i=1;i<=n;i++)
		cin>>a[i];
	for(int i=1;i<=q;i++)
		cin>>qry[i].l>>qry[i].r,qry[i].id=i;
	sort(qry+1,qry+q+1,cmp);
	int x=1,y=0;
	for(int i=1;i<=q;i++){
		int qx=qry[i].l,qy=qry[i].r;
		while(x>qx) add(--x);
		while(y<qy) add(++y);
		while(x<qx) del(x++);
		while(y>qy) del(y--);
		ans[qry[i].id]=(tot==qy-qx+1);
	}
	for(int i=1;i<=q;i++)
		cout<<(ans[i]?"Yes\n":"No\n");
	return 0;
}

P2709

维护 \(tot\) 表示 \(\sum c_i^2\) 以及 \(c_i\)，每次增加时先 \(tot\) 先减再加即可，见代码。

实现

#include<bits/stdc++.h>
#define int long long
using namespace std;

const int N=1e5+5;
int n,m,k,t,tot;
int ans[N],cnt[N],a[N];
struct Q{
	int l,r,id;
}q[N];

bool cmp(Q &x,Q &y){
	if(x.l/t!=y.l/t)
		return x.l<y.l;
	return x.r<y.r;
}
void add(int x){
	tot-=cnt[a[x]]*cnt[a[x]];
	cnt[a[x]]++;
	tot+=cnt[a[x]]*cnt[a[x]];
}
void del(int x){
	tot-=cnt[a[x]]*cnt[a[x]];
	cnt[a[x]]--;
	tot+=cnt[a[x]]*cnt[a[x]];
}

signed main(){
	ios::sync_with_stdio(0);
	cin.tie(0);
	cin>>n>>m>>k,t=sqrt(n);
	for(int i=1;i<=n;i++)
		cin>>a[i];
	for(int i=1;i<=m;i++)
		cin>>q[i].l>>q[i].r,q[i].id=i;
	sort(q+1,q+m+1,cmp);
	int x=1,y=0;
	for(int i=1;i<=m;i++){
		int qx=q[i].l,qy=q[i].r;
		while(x>qx) add(--x);
		while(y<qy) add(++y);
		while(x<qx) del(x++);
		while(y>qy) del(y--);
		ans[q[i].id]=tot;
	}
	for(int i=1;i<=m;i++)
		cout<<ans[i]<<'\n';
	return 0;
}

P4396

这题有值域和区间上的两个约束条件，显然区间内统计个数和种类数都可以用莫队很方便的解决。

至于值域方面，我们采用与莫队相近的分块解决，即对值域进行分块，对于每个块维护自己的个数与种类数，然后整块累加刚刚维护的那玩意，散块直接暴力扫描即可。

实现

#include <cstdio>
#include <iostream>
#include <algorithm>
#include <cstring>
#include <string>
#include <stdlib.h>
#include <vector>
#include <queue>
#include <cmath>
#include <stack>
#include <map>
#include <set>
#define int long long
using namespace std;

const int N=1e5+5;
int n,m,t,mx=1e5;
int a[N],cnt[N];
int L[N],R[N],pos[N];
int sum[N][2],ans[N][2];
struct Q{
	int l,r,a,b,id;
}q[N];

bool cmp(Q &x,Q &y){
	if(x.l/t!=y.l/t)
		return x.l<y.l;
	if((x.l/t)&1)
		return x.r<y.r;
	return x.r>y.r;
}
void add(int x){
	cnt[a[x]]++;
	sum[pos[a[x]]][0]++;
	if(cnt[a[x]]==1)
		sum[pos[a[x]]][1]++;
}
void del(int x){
	cnt[a[x]]--;
	sum[pos[a[x]]][0]--;
	if(!cnt[a[x]])
		sum[pos[a[x]]][1]--;
}
void qry(int x){
	int qid=q[x].id,ql=q[x].a,qr=q[x].b;
	int pl=pos[ql],pr=pos[qr];
	for(int i=pl+1;i<pr;i++)
		ans[qid][0]+=sum[i][0],ans[qid][1]+=sum[i][1];
	if(pl==pr){
		for(int i=ql;i<=qr;i++){
			ans[qid][0]+=cnt[i];
			if(cnt[i])
				ans[qid][1]++;
		}
	}
	else{
		for(int i=ql;i<=R[pl];i++){
			ans[qid][0]+=cnt[i];
			if(cnt[i])
				ans[qid][1]++;
		}
		for(int i=L[pr];i<=qr;i++){
			ans[qid][0]+=cnt[i];
			if(cnt[i])
				ans[qid][1]++;
		}
	}
}
void solve(){
	int x=1,y=0;
	for(int i=1;i<=m;i++){
		while(x>q[i].l) add(--x);
		while(y<q[i].r) add(++y);
		while(x<q[i].l) del(x++);
		while(y>q[i].r) del(y--);
		qry(i);
	}
} 

signed main(){
	ios::sync_with_stdio(0);
	cin.tie(0);
	cin>>n>>m;
	for(int i=1;i<=n;i++)
		cin>>a[i];
	int siz=sqrt(mx);
	t=mx/siz;
	for(int i=1;i<=m;i++)
		cin>>q[i].l>>q[i].r>>q[i].a>>q[i].b,q[i].id=i;
	sort(q+1,q+m+1,cmp);
	for(int i=1;i<=t;i++){
		L[i]=(i-1)*siz+1;
		R[i]=i*siz;
	}
	if(R[t]<mx){
		t++;
		L[t]=R[t-1]+1;
		R[t]=mx;
	}
	for(int i=1;i<=t;i++)
		for(int j=L[i];j<=R[i];j++)
			pos[j]=i;
	solve();
	for(int i=1;i<=m;i++)
		cout<<ans[i][0]<<' '<<ans[i][1]<<'\n';
	return 0;
}

P3709

这个题，我们发现要让 rp 最大化，显然从小到大放置是最优的，问题转化为将一个区间划分为尽可能少的最长上升子序列，不难发现答案即为区间众数出现的次数，可根据下图理解。

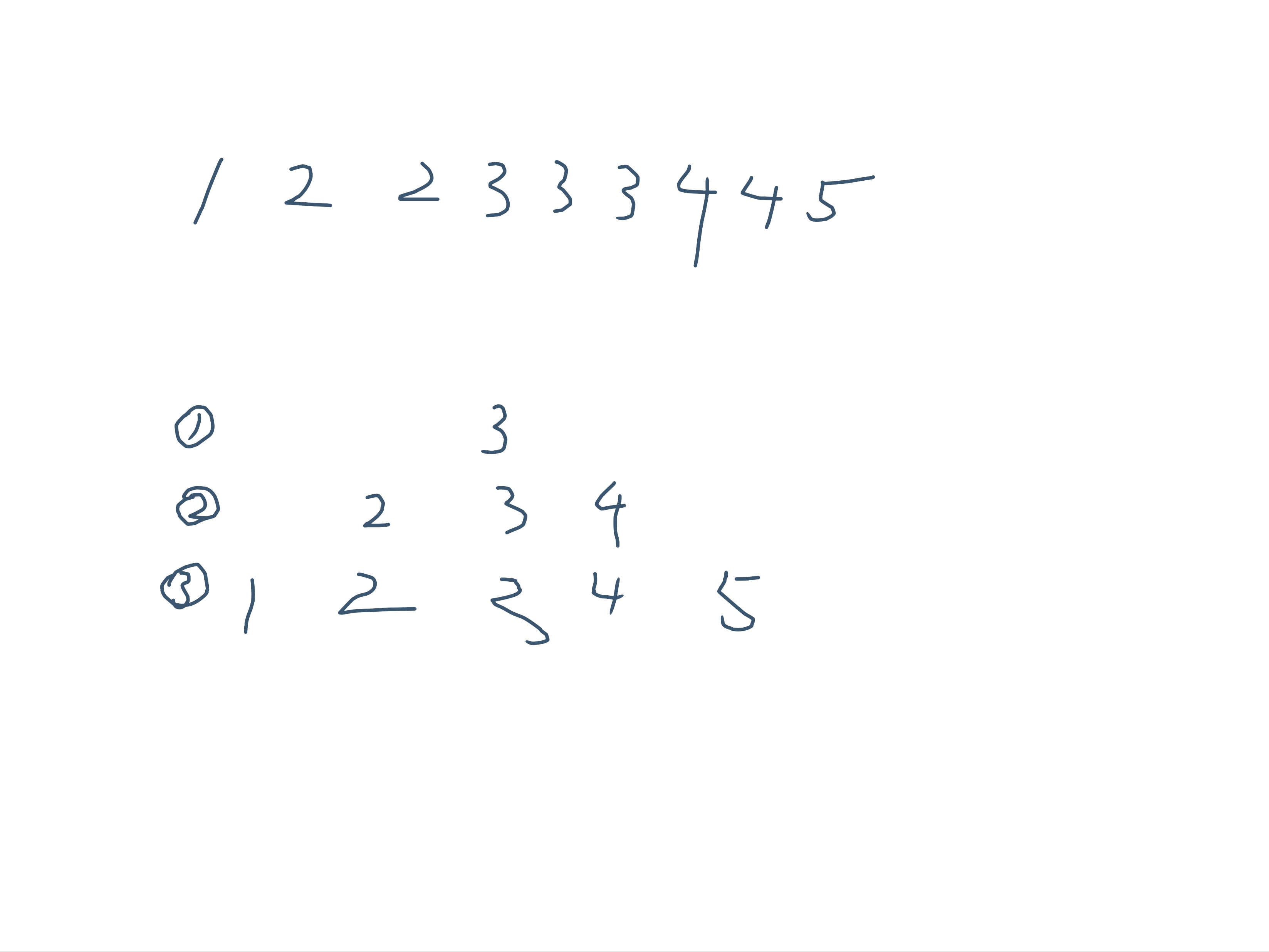
然后我们需要使用莫队维护众数出现的次数，增加元素的时候是好维护的（取 \(\max\) 即可），但删除时就不好做了。于是我们需要另外维护一个元素出现次数的出现次数，每当删除前众数出现次数的出现次数只有一个了，说明删除后众数出现次数会少一个，但容易发现它一定仍然是众数。

实现

#include<bits/stdc++.h>
//#define int long long
using namespace std;

const int N=2e5+5;
int n,m,t,tot;
int ans[N],cnt[N],a[N],aa[N],buc[N];
struct Q{
	int l,r,id;
}q[N];

bool cmp(Q &x,Q &y){
	if(x.l/t!=y.l/t)
		return x.l<y.l;
	if((x.l/t)&1)
		return x.r<y.r;
	return x.r>y.r;
}
void add(int x){
	buc[cnt[a[x]]]--;
	cnt[a[x]]++;
	buc[cnt[a[x]]]++;
	tot=max(tot,cnt[a[x]]);
}
void del(int x){
	if(buc[cnt[a[x]]]==1&&tot==cnt[a[x]])
		tot--;
	buc[cnt[a[x]]]--;
	cnt[a[x]]--;
	buc[cnt[a[x]]]++;
}

signed main(){
	ios::sync_with_stdio(0);
	cin.tie(0);
	cin>>n>>m,t=sqrt(n);
	for(int i=1;i<=n;i++)
		cin>>a[i],aa[i]=a[i];
	sort(aa+1,aa+n+1);
	int len=unique(aa+1,aa+n+1)-aa-1;
	for(int i=1;i<=n;i++)
		a[i]=lower_bound(aa+1,aa+len+1,a[i])-aa;
	for(int i=1;i<=m;i++)
		cin>>q[i].l>>q[i].r,q[i].id=i;
	sort(q+1,q+m+1,cmp);
	int x=1,y=0;
	for(int i=1;i<=m;i++){
		int qx=q[i].l,qy=q[i].r;
		while(x>qx) add(--x);
		while(y<qy) add(++y);
		while(x<qx) del(x++);
		while(y>qy) del(y--);
		ans[q[i].id]=-tot;
	}
	for(int i=1;i<=m;i++)
		cout<<ans[i]<<'\n';
	return 0;
}

CF340E

XOR 两个性质：

\(a \oplus b=c \iff a \oplus c=b\)
可以做前缀 XOR。

根据性质二，可以将这题转化为点对查询，再根据性质一可以转化为问一个数的出现次数，然后用莫队做即可。

实现

#include <cstdio>
#include <iostream>
#include <algorithm>
#include <cstring>
#include <string>
#include <stdlib.h>
#include <vector>
#include <queue>
#include <cmath>
#include <stack>
#include <map>
#include <set>
using namespace std;
#define int long long

const int N=2e6+5;
int n,m,k,t,tot;
int a[N],cnt[N],ans[N];
struct Q{
	int l,r,id;
}q[N];

bool cmp(Q &x,Q &y){
	if(x.l/t!=y.l/t)
		return x.l<y.l;
	if((x.l/t)&1)
		return x.r<y.r;
	return x.r>y.r;
}
void add(int x){ tot+=cnt[a[x]^k],cnt[a[x]]++; }
void del(int x){ cnt[a[x]]--,tot-=cnt[a[x]^k]; }
void solve(){
	int l=0,r=-1;
	for(int i=1;i<=m;i++){
		for(;l>q[i].l-1;add(--l));
		for(;r<q[i].r;add(++r));
		for(;l<q[i].l-1;del(l++));
		for(;r>q[i].r;del(r--));
		ans[q[i].id]=tot;
	}
}

signed main(){
	ios::sync_with_stdio(0);
	cin.tie(0);
	cin>>n>>m>>k;
	t=sqrt(n);
	int tmp=0;
	for(int i=1;i<=n;i++)
		cin>>a[i],a[i]^=a[i-1];
	for(int i=1;i<=m;i++)
		cin>>q[i].l>>q[i].r,q[i].id=i;
	sort(q+1,q+m+1,cmp);
	solve();
	for(int i=1;i<=m;i++)
		cout<<ans[i]<<'\n';
	return 0;
}

P5268

推柿子：

\[\sum\limits_{x=0}^\infty \text{get}(l_1,r_1,x)\times \text{get}(l_2,r_2,x)\\ = \sum\limits_{x=0}^\infty (\text{get}(1,r_1,x)-\text{get}(1,l_1-1,x)) \times (\text{get}(1,r_2,x)-\text{get}(1,l_2-1,x))\\ = \sum\limits_{x=0}^\infty \text{get}(1,r_1,x) \times \text{get}(1,r_2,x) - \text{get}(1,r_1,x) \times \text{get}(1,l_2-1,x) - \text{get}(1,l_1-1,x) \times \text{get}(1,r_2,x) + \text{get}(1,l_1-1,x) \times \text{get}(1,l_2-1,x) \]

现在，我们的询问被拆成了四部分：

求 \(\sum\limits_{x=0}^\infty \text{get}(1,r_1,x) \times \text{get}(1,r_2,x)\)
求 \(\sum\limits_{x=0}^\infty \text{get}(1,r_1,x) \times \text{get}(1,l_2-1,x)\)
求 \(\sum\limits_{x=0}^\infty \text{get}(1,l_1-1,x) \times \text{get}(1,r_2,x)\)
求 \(\sum\limits_{x=0}^\infty \text{get}(1,l_1-1,x) \times \text{get}(1,l_2-1,x)\)

考虑使用莫队维护。

但是这次，我们并非维护一个区间，而是维护两个前缀。

当左边的加进来一个数，应当加上其在右边前缀的贡献，减去同理，右边反之。

于是我们很容易发现我们在哪边的前缀操作，应当算上另一边产生的贡献。

然后这个题做完了，注意初始光标为 \(0,0\)。

说起来貌似十分复杂，但实现是简单的。

实现

#include<bits/stdc++.h>
#define int long long
using namespace std;

const int N=2e5+5;
int n,m,mm,t,tot;
int a[N],ans[N],cnt[N],lt[N],rt[N];
struct Q{
	int l,r,id,val;
}q[N];

bool cmp(Q &x,Q &y){
	if(x.l/t!=y.l/t)
		return x.l<y.l;
	if((x.l/t)&1)
		return x.r<y.r;
	return x.r>y.r;
}
void addl(int x){
	lt[a[x]]++;
	tot+=rt[a[x]];
}
void dell(int x){
	lt[a[x]]--;
	tot-=rt[a[x]];
}
void addr(int x){
	rt[a[x]]++;
	tot+=lt[a[x]];
}
void delr(int x){
	rt[a[x]]--;
	tot-=lt[a[x]];
}

signed main(){
	ios::sync_with_stdio(0);
	cin.tie(0);
	cin>>n,t=sqrt(n);
	for(int i=1;i<=n;i++)
		cin>>a[i];
	cin>>m;
	for(int i=1,l1,r1,l2,r2;i<=m;i++){
		cin>>l1>>r1>>l2>>r2;
		q[++mm]={r1,r2,i,1};
		q[++mm]={l2-1,r1,i,-1};
		q[++mm]={l1-1,r2,i,-1};
		q[++mm]={l1-1,l2-1,i,1};
	}
	sort(q+1,q+mm+1,cmp);
	int x=0,y=0;
	for(int i=1;i<=mm;i++){
		int qx=q[i].l,qy=q[i].r;
		while(x<qx) addl(++x);
		while(x>qx) dell(x--);
		while(y<qy) addr(++y);
		while(y>qy) delr(y--);
		ans[q[i].id]+=tot*q[i].val;
	}
	for(int i=1;i<=m;i++)
		cout<<ans[i]<<'\n';
	return 0;
}

这是法一，接下来我们来个无脑纯分块做法（idea by xkr）。

对于两个块，我们按如下方式处理贡献：

左边区间对右边整块产生贡献
右边整块对左边散块产生贡献
右边散块对左边散块产生贡献

第三个开桶暴力计算即可，前两个可以维护一个 \(sum_{i,j}\) 表示前 \(j\) 个数对块 \(i\) 产生的贡献，用前缀和做即可，具体见代码。

实现

#include <cstdio>
#include <iostream>
#include <algorithm>
#include <cstring>
#include <string>
#include <stdlib.h>
#include <vector>
#include <queue>
#include <cmath>
#include <stack>
#include <map>
#include <set>
#define int long long
using namespace std;

const int N=2e5+5,M=5e2+5;
int n,m;
int a[N],pos[N],L[N],R[N],sum[M][N],cnt[N];
struct Q{
	int l1,r1,l2,r2,id;
}q[N];

void getsum(int x){
	for(int i=L[x];i<=R[x];i++)
		cnt[a[i]]++;
	for(int i=1;i<=n;i++)
		sum[x][i]=sum[x][i-1]+cnt[a[i]];
	for(int i=L[x];i<=R[x];i++)
		cnt[a[i]]--;
}
void init(){
	int t=sqrt(n);
	for(int i=1;i<=t;i++){
		L[i]=(i-1)*sqrt(n)+1;
		R[i]=i*sqrt(n);
	}
	if(R[t]<n){
		t++;
		L[t]=R[t-1]+1;
		R[t]=n;
	}
	for(int i=1;i<=t;i++)
		for(int j=L[i];j<=R[i];j++)
			pos[j]=i;
	for(int i=1;i<=t;i++)
		getsum(i);
}
int qry(int l1,int r1,int l2,int r2){
	int ans=0;
	int p1=pos[l1],q1=pos[r1],p2=pos[l2],q2=pos[r2];
	for(int i=p2+1;i<q2;i++)
		ans+=sum[i][r1]-sum[i][l1-1];
	for(int i=p1+1;i<q1;i++){
		if(p2!=q2)
			ans+=sum[i][R[p2]]-sum[i][l2-1]+sum[i][r2]-sum[i][L[q2]-1];
		else
			ans+=sum[i][r2]-sum[i][l2-1];
	}
	if(p2!=q2){
		for(int i=l2;i<=R[p2];i++)
			cnt[a[i]]++;
		for(int i=L[q2];i<=r2;i++)
			cnt[a[i]]++;
	}
	else
		for(int i=l2;i<=r2;i++)
			cnt[a[i]]++;
	if(p1!=q1){
		for(int i=l1;i<=R[p1];i++)
			ans+=cnt[a[i]];
		for(int i=L[q1];i<=r1;i++)
			ans+=cnt[a[i]];
	}
	else
		for(int i=l1;i<=r1;i++)
			ans+=cnt[a[i]];
	if(p2!=q2){
		for(int i=l2;i<=R[p2];i++)
			cnt[a[i]]--;
		for(int i=L[q2];i<=r2;i++)
			cnt[a[i]]--;
	}
	else
		for(int i=l2;i<=r2;i++)
			cnt[a[i]]--;
	return ans;
}

signed main(){
	ios::sync_with_stdio(0);
	cin.tie(0);
	cin>>n;
	for(int i=1;i<=n;i++)
		cin>>a[i];
	init();
	cin>>m;
	for(int i=1,l1,r1,l2,r2;i<=m;i++){
		cin>>l1>>r1>>l2>>r2;
		cout<<qry(l1,r1,l2,r2)<<'\n';
	}
	return 0;
}

P3245

比较巧妙。

看到只有询问，考虑莫队。

因为莫队只擅长处理元素约束条件，所以考虑使用 hash 将区间映射成数字。

即维护一个后缀 hash 值 \(num_i\)，那么区间 \([l,r]\) 可以表示为 \(\frac{num_l-num_{r+1}}{10^{r-l+1}}\)，它必须满足 \(\equiv 0 \pmod{p}\)。

若 \(p\) 与 \(10\) 互质，则问题转化为求 \(num_l\) 与 \(num_{r+1}\) 模 \(p\) 同余的点对数，直接莫队维护就好了。

若不互质，此时分母为 \(0\)，无法使用上述方法。于是问题又转化为 \([l,r]\) 中有多少子区间满足个位为 \(0,2,4,6,8/0,5\)，前缀和思想统计即可。

实现

#include <cstdio>
#include <iostream>
#include <algorithm>
#include <cstring>
#include <string>
#include <stdlib.h>
#include <vector>
#include <queue>
#include <cmath>
#include <stack>
#include <map>
#include <set>
#define int long long
using namespace std;

const int N=2e5+5;
int p,n,m,t,tot;
string s;
int a[N],num[N],tmp[N],cnt[N],ans[N];
int tag[N],spos[N],snum[N];
struct Q{
	int l,r,id;
}q[N];

void solve(){
	if(p==2)
		tag[0]=tag[2]=tag[4]=tag[6]=tag[8]=1;
	else if(p==5)
		tag[0]=tag[5]=1;
	for(int i=1;i<=n;i++){
		snum[i]=snum[i-1]+tag[a[i]];
		spos[i]=spos[i-1]+tag[a[i]]*i;
	}
	for(int i=1,l,r;i<=m;i++){
		cin>>l>>r;
		cout<<(spos[r]-spos[l-1]-(snum[r]-snum[l-1])*(l-1))<<'\n';
	}
}
bool cmp(Q &x,Q &y){
	if(x.l/t!=y.l/t)
		return x.l<y.l;
	if((x.l/t)&1)
		return x.r<y.r;
	return x.r>y.r;
}
void D(){
	for(int i=1;i<=n+1;i++)
		tmp[i]=num[i];
	sort(tmp+1,tmp+n+2);
	int len=unique(tmp+1,tmp+n+2)-tmp-1;
	for(int i=1;i<=n+1;i++)
		num[i]=lower_bound(tmp+1,tmp+len+1,num[i])-tmp;
}
void add(int x){
	tot-=cnt[num[x]]*(cnt[num[x]]-1)/2;
	cnt[num[x]]++;
	tot+=cnt[num[x]]*(cnt[num[x]]-1)/2;
}
void del(int x){
	tot-=cnt[num[x]]*(cnt[num[x]]-1)/2;
	cnt[num[x]]--;
	tot+=cnt[num[x]]*(cnt[num[x]]-1)/2;
}

signed main(){
	ios::sync_with_stdio(0);
	cin.tie(0);
	cin>>p>>s>>m;
	for(auto i:s)
		a[++n]=(i-'0');
	if(p==2||p==5)
		solve(),exit(0);
	t=sqrt(n);
	for(int i=n,c=1;i>=1;i--,c=c*10%p)
		num[i]=(a[i]*c%p+num[i+1])%p;
	D();
	for(int i=1;i<=m;i++)
		cin>>q[i].l>>q[i].r,q[i].r++,q[i].id=i;
	sort(q+1,q+m+1,cmp);
	int x=1,y=0;
	for(int i=1;i<=m;i++){
		int qx=q[i].l,qy=q[i].r;
		while(x>qx) add(--x);
		while(y<qy) add(++y);
		while(x<qx) del(x++);
		while(y>qy) del(y--);
		ans[q[i].id]=tot;
	}
	for(int i=1;i<=m;i++)
		cout<<ans[i]<<'\n';
	return 0;
}

CF136E

糖题，不想讲。

实现

#include <cstdio>
#include <iostream>
#include <algorithm>
#include <cstring>
#include <string>
#include <stdlib.h>
#include <vector>
#include <queue>
#include <cmath>
#include <stack>
#include <map>
#include <set>
#define int long long
using namespace std;

const int N=1e5+5;
int n,m,t,tot;
int ans[N],cnt[N],a[N],tmp[N],aa[N];
struct Q{
	int l,r,id;
}q[N];

bool cmp(Q &x,Q &y){
	if(x.l/t!=y.l/t)
		return x.l<y.l;
	return x.r<y.r;
}
void add(int x){
	if(cnt[a[x]]==aa[x])
		tot--;
	cnt[a[x]]++;
	if(cnt[a[x]]==aa[x])
		tot++;
}
void del(int x){
	if(cnt[a[x]]==aa[x])
		tot--;
	cnt[a[x]]--;
	if(cnt[a[x]]==aa[x])
		tot++;
}
void D(){
	for(int i=1;i<=n;i++)
		aa[i]=tmp[i]=a[i];
	sort(tmp+1,tmp+n+1);
	int len=unique(tmp+1,tmp+n+1)-tmp-1;
	for(int i=1;i<=n;i++)
		a[i]=lower_bound(tmp+1,tmp+len+1,a[i])-tmp;
}

signed main(){
	ios::sync_with_stdio(0);
	cin.tie(0);
	cin>>n>>m,t=sqrt(n);
	for(int i=1;i<=n;i++)
		cin>>a[i];
	D();
	for(int i=1;i<=m;i++)
		cin>>q[i].l>>q[i].r,q[i].id=i;
	sort(q+1,q+m+1,cmp);
	int x=1,y=0;
	for(int i=1;i<=m;i++){
		int qx=q[i].l,qy=q[i].r;
		while(x>qx) add(--x);
		while(y<qy) add(++y);
		while(x<qx) del(x++);
		while(y>qy) del(y--);
		ans[q[i].id]=tot;
	}
	for(int i=1;i<=m;i++)
		cout<<ans[i]<<'\n';
	return 0;
}

总结：

什么时候考虑莫队（满足以下任意一个条件）？
- 只有询问。
- 对数字有约束条件。
- 可以处理增量。
零散的一些技巧：
- 前缀和思想、hash 思想、推柿子思想。
- XOR 两大性质。

posted @ 2025-03-29 21:39 _KidA 阅读(27) 评论(0) 收藏举报

刷新页面返回顶部

XOF.

Making all his nowhere blogs for nobody.

莫队

莫队