辛普森积分法

1 定积分

在学习辛普森积分之前，我们需要了解一些基本的积分知识。

1.1 定义

设函数 \(f(x)\) 在区间 \([a,b]\) 上有界，在 \([a,b]\) 中插入若干个分点 \(a=x_0<x_1<\cdots<x_n=b\)，将区间 \([a,b]\) 分成 \(n\) 个小区间，每个小区间的长度以此为 \(\Delta x_i =x_i-x_{i-1}\)。在各个小区间上任取一点 \(\xi_i\in [x_{i-1},x_i]\)，做乘积 \(f(\xi_i)\Delta x_i\) 并求和，称其为函数 \(f\) 在区间 \([a,b]\) 上的黎曼和。即：

\[S=\sum_{i=1}^n f(\xi_i)\Delta x_i \]

记 \(\lambda =\max(\Delta x_1,\Delta x_2,\cdots, \Delta x_n)\)，如果不论对 \([a,b]\) 怎样分，不论怎样取 \(\xi_i\)，当 \(\lambda\to 0\) 时，\(S\) 总趋于一个确定的极限 \(I\)，我们就称极限 \(I\) 为函数 \(f(x)\) 在区间 \([a,b]\) 上的定积分，记作 \(\int_a^b f(x)dx\)，即：

\[\int_a^b f(x) dx=I=\lim_{\lambda\to 0}\sum_{i=0}^n f(\xi_i)\Delta x_i \]

其中 \(f(x)\) 叫被积函数，\(f(x)dx\) 叫被积表达式，\(x\) 叫积分变量，\(a\) 叫做积分下限，\(b\) 叫做积分上限，\([a,b]\) 叫做积分区间。

直观上来讲，\(f(x)\) 在区间 \([a,b]\) 上的定积分实际上就是 \(f(x)\) 与直线 \(x=a,x=b\) 以及 \(x\) 轴围成的曲边梯形的正向面积，也就是所谓曲线下面积。

注意这里我们需要定义：

• \(\int_a^a f(x)dx=0\)。
• \(\int_a^b f(x)dx =-\int_b^a f(x)dx\)。

1.2 性质

定积分有如下基本性质：

• 线性性，即：

  \[\int_a^b [\alpha f(x)+\beta g(x)]dx=\alpha \int_a^b f(x)dx+\beta\int_a^b g(x)dx \]

• 对区间有可加性，即：

  \[\int_a^b f(x)dx=\int_a^c f(x)dx+\int_c^b f(x)dx \]

• 保号性，即对于 \(a<b\)，如果在区间 \([a,b]\) 上 \(f(x)\ge 0\)，则：

  \[\int_a^b f(x)dx\ge 0 \]

1.3 牛顿-莱布尼茨公式

对于朴素的积分计算，我们有牛顿-莱布尼茨公式（又称微积分基本定理），是用于求定积分最常用且简单的方法。对于两个函数 \(f(x)\) 和 \(F(x)\)，如果 \(F'(x)=f(x)\)，那么我们有：

\[\int_a^b f(x)dx=F(b)-F(a) \]

上式右侧有时也记作 \(F(x)|_a^b\)。只要我们可以求出 \(f(x)\) 的原函数 \(F(x)\)，那么就能求出其积分值。

举个例子：求 \(\int_0^1 x^2 dx\) 的值。

我们知道 \(f(x)=x^2\) 的原函数应该是 \(F(x)=\tfrac 13 x^3+C\)，其中 \(C\) 为常数。那么根据牛顿-莱布尼茨公式可以得出：

\[\int_0^1 x^2 dx=(\dfrac 13\times 1^3+C)-(\dfrac 13\times 0^3+C)=\dfrac 13 \]

这就是关于定积分的基本知识，下面我们来看辛普森积分。

2 辛普森积分法

很多情况下，我们需要快速准确的求出一个积分的近似值。而辛普森积分法就是这样一种求数值积分的方法。

2.1 普通辛普森法

根据牛顿-莱布尼茨公式我们可以算出一些函数的积分值。但是有一些函数不一定有原函数 \(F(x)\) 或者原函数较难求解，此时我们考虑用一个易于积分的近似函数来替换掉原来的被积函数，从而得到一个近似值。我们称这个方法为牛顿-柯特斯公式：

\[I=\int_a^b f(x)dx\cong \int_a^b f_n(x) dx \]

其中 \(f_n(x)\) 是一个 \(n\) 次多项式。如果我们取 \(n=1\)，那么实际上我们就是将 \(a,b\) 两点的连线看作原函数来进行积分，这就是一阶牛顿-柯特斯闭型积分公式，也就是所谓的梯形法则。

而辛普森积分法实际上就是二阶牛顿-柯特斯闭型积分公式，也就是说我们用一个二次函数去适配原函数。众所周知，三个点可以确定一个二次函数，所以我们还需要在函数上找一个点，取 \(c=\tfrac {a+b}2\) 这个点即可。此时我们有：

\[\int_a^b f(x)dx\cong \int_a^b f_2(x)dx =\dfrac {b-a}6 [f(a)+4f(c)+f(b)] \]

这就是所谓的辛普森积分法了。

下面我们证明一下辛普森积分法。设由 \(a,b,c\) 三点得到的二次函数为 \(f_2(x)=Ax^2+Bx+C\)，那么显然其原函数 \(F_2(x)=\tfrac A3 x^3 +\tfrac B2 x^2 +Cx+\alpha\)，其中 \(\alpha\) 是常数。由牛顿-莱布尼茨公式可得：

\[\begin{aligned} \int_a^b f(x)dx&\cong \int_a^b f_2(x)dx\\ &=F_2(b)-F_2(a)\\ &= \frac A3(b^3-a^3)+\dfrac B2(b^2-a^2)+C(b-a)\\ &=\frac A3(b-a)(b^2+ab+a^2)+\dfrac B2 (b-a)(b+a)+C(b-a)\\ &=\dfrac{(b-a)}6 [2A(a^2+ab+b^2)+3B(a+b)+6C]\\ &=\dfrac{(b-a)}6 [Aa^2+Ba+C+A(a^2+2ab+b^2)+2B(a+b)+4C+Ab^2+Bb+C]\\ &=\dfrac{(b-a)}6 [(Aa^2+Ba+C)+4(A(\frac{a+b}2)^2+B(\frac{a+b}2)+C)+(Ab^2+Bb+C)]\\ &=\dfrac{(b-a)}6 [(Aa^2+Ba+C)+4(Ac^2+Bc+C)+(Ab^2+Bb+C)]\\ &=\dfrac{(b-a)}6 [f_2(a)+4f_2(c)+f_2(b)]\\ &=\dfrac{(b-a)}6 [f(a)+4f(c)+f(b)]\\ \end{aligned} \]

如此我们就可以得到原函数定积分的近似值。

2.2 自适应辛普森法

对于一个次数较高或者图像不接近二次函数的函数来讲，直接使用上面的辛普森法准确率显然很低。而自适应辛普森法就是用于解决这个问题的。

我们考虑对积分区间分段，如果我们能让分出来的每一段都接近二次函数，那么准确度就会大大提高。现在的问题是如何分段，如果段数过大会超时，如果段数过小准确度就不高。

考虑如下划分方法，我们先对当前区间 \([a,b]\) 做一次普通辛普森求出其积分值 \(A\)，然后再对 \([a,c],[c,b]\) 两个区间求出积分值 \(A_1,A_2\)。由积分的区间可加性，只要 \(A\) 与 \(A_1+A_2\) 相差不至于过大，我们就认为当前区间足够接近二次函数，不再进行分段；否则继续向下递归求出 \(A_1,A_2\) 的准确近似值后返回答案。

然后就是一些优化，在保证准确度的情况下减小运行时间：

• 考虑到有可能 \(A,A_1,A_2\) 的误差都很大，但是其差值恰好较小，此时我们依然认为其是准确的。我们考虑人为设定一个递归阈值，只有当递归层数超过该阈值的时候才会考虑直接退出。

• 为了防止小误差相加后得到的误差变大，我们在递归的时候需要将判定合法的误差阈值逐渐减小。

• 在求解的过程中，我们很有可能多次求函数值 \(f(x)\)，不妨利用记忆化减小运算常数。

不过上面的优化都是有概率负优化的，比如说模板题用优化 1 就不如不用，不过大部分时候全部加上是更好的。

2.3 代码

模板题：【模板】自适应辛普森法 1，代码如下：

#include <bits/stdc++.h>

using namespace std;

const int Maxn = 2e5 + 5;
const int Inf = 2e9;

double a, b, c, d, l, r;

unordered_map <double, double> mp;
double f(double x) {
	if(mp.count(x)) return mp[x];//记忆化已经求过的函数值
	return mp[x] = (c * x + d) / (a * x + b);
}

double simpson(double l, double r) {//普通辛普森积分法
	double mid = (l + r) / 2;
	return (f(l) + f(r) + 4 * f(mid)) * (r - l) / 6;
}

double asr(double l, double r, double ans, double eps, int stp) {
	double mid = (l + r) / 2;
	double fl = simpson(l, mid), fr = simpson(mid, r);//左右区间积分值
	if(fabs(fl + fr - ans) <= 15 * eps/*误差不超过阈值*/ && stp < 0/*超过递归阈值*/) {
		return fl + fr + (fl + fr - ans) / 15/*进一步修正误差*/;//返回答案
	}
	return asr(l, mid, fl, eps / 2, stp - 1) + asr(mid, r, fr, eps / 2, stp - 1);
    //递归求解
}

int main() {
	ios::sync_with_stdio(0);
	cin.tie(0), cout.tie(0);
	cin >> a >> b >> c >> d >> l >> r;
	double ans = asr(l, r, simpson(l, r), 1e-6, 5);
	cout << fixed << setprecision(6) << ans << '\n';
	return 0;
}

2.4 例题

实际上，辛普森积分在 OI 中的用途比较不大，除了暴力求积分以外，最常见的用途就是求图形面积并。

例 1 [CQOI2005] 三角形面积并

\(\text{Link}\)

实际上此题可以直接扫描线，不过我们也可以用辛普森积分求解。

考虑设一个函数 \(f(a)\) 表示在原平面直角坐标系上 \(x=a\) 这条直线与三角形相交的线段长度。那么我们要求的就是从 \(f(-10^6)\) 到 \(f(10^6)\) 的取值之和，也就是：

\[\int_{-10^6}^{10^6} f(x)dx \]

那么我们直接上辛普森积分即可，问题就在于 \(f(a)\) 的求解。我们直接暴力枚举每个三角形，计算出每个三角形与这条直线相交的长度，然后求一遍线段的并即可，单次求解复杂度是 \(O(n\log n)\) 的。

接下来就是辛普森积分较扫描线的劣势了：它需要一定的卡精度技巧才能通过。对于此题而言，不仅要加入上面提到的优化，由于这个函数中很有可能有一大段都是 \(0\)，所以我们还需要分段求解积分才能通过。

例 2 [NOI2005] 月下柠檬树

\(\text{Link}\)

实际上这道题积分部分较为简单，难点在于前面的分析上。

首先投影是平行光的投影，所以圆的半径不会改变，只有两个圆之间的距离会改变。以柠檬树为原点建立平面直角坐标系，对于一个离地面高度为 \(h\) 的圆来讲，它的 \(x\) 坐标应该落在 \(\tfrac{h}{\tan \alpha}\) 上。

不过显然这棵树的投影不止是这些分界上的圆，每个横截面上的圆也会构成阴影。考虑一个圆台的两个圆构成的阴影，则不难想像到该圆台中间任意横截面构成的投影正好填在了两圆的公切线之间，如下图所示：

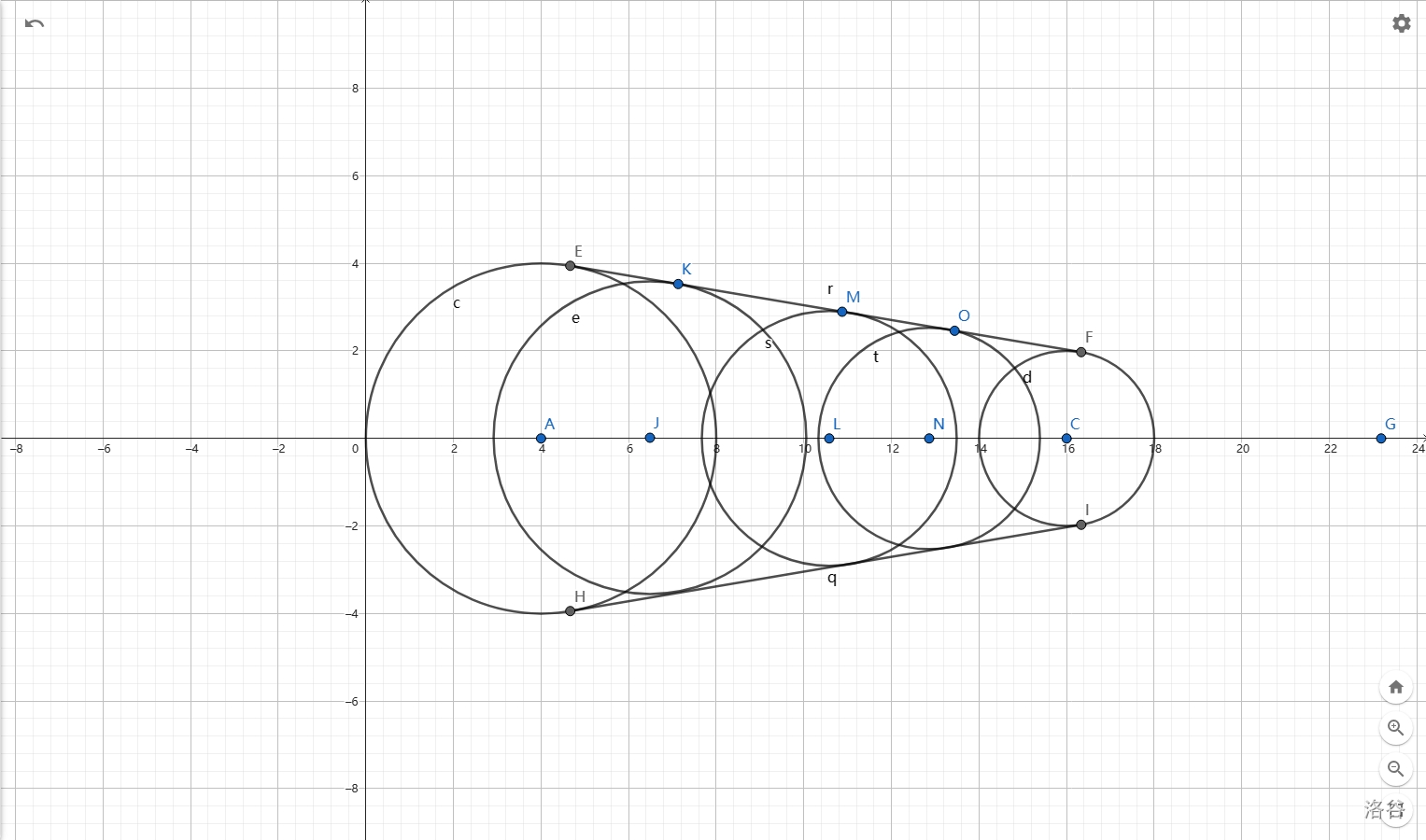
圆 \(A,C\) 为圆台的上下底面，那么中间的圆构成的投影正好在两圆公切线之间，即 \(EF,HI\) 之间。

所以除了圆以外，我们还要求出两条切线的方程及定义域，也就是两个切点。由于图形一定关于 \(x\) 轴对称，所以我们只需要求出一边即可。下面我们以上面那条切线为例：

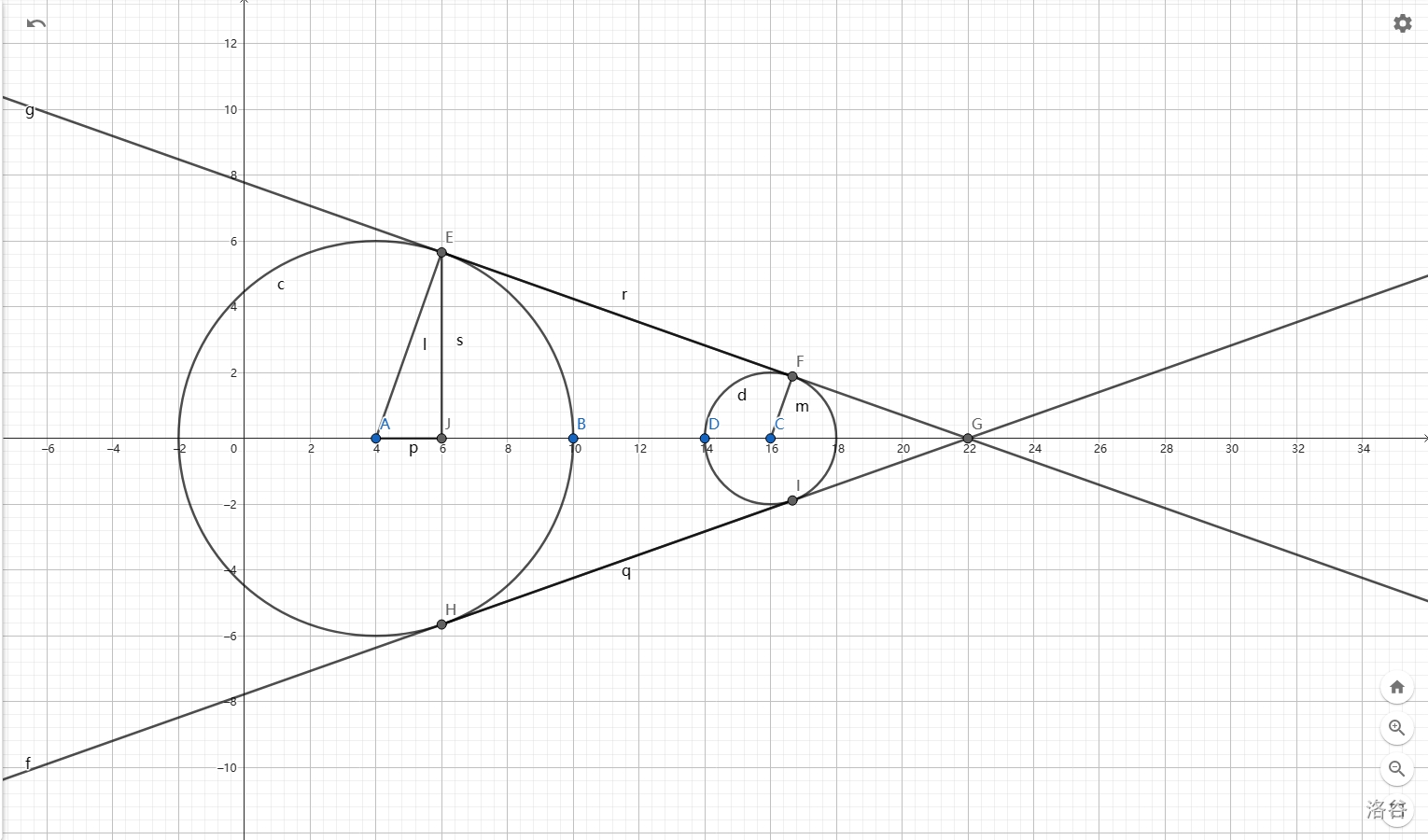
如上图所示。我们已知的有两圆半径（即 \(AE,CF\)）。设切线与 \(x\) 轴交点 \(G\) 的 \(x\) 坐标为 \(x_G\)，由于 \(\triangle AEG\sim \triangle CFG\)，所以可以得到：

\[\frac{x_G-x_A}{x_G-x_C}=\frac{AE}{CF} \]

然后可以轻易解出 \(x_G\)。于是就可以得到 \(CG,AG\) 的值，然后利用勾股定理即可得出 \(FG,EG\) 的值。接下来求出 \(\sin \angle EGA\) 的值，作 \(EJ\perp x\) 轴，然后 \(EJ\) 就等于 \(EG\sin\angle EGA\)，再利用勾股定理即可求出 \(AJ\) 的值，于是就可以求出 \(E\) 的坐标。对于 \(F\) 同理。于是两切点坐标均可得出。

注意对于两圆半径大小关系进行分类讨论，尤其注意半径相等时不能利用上述方法求解，不过此时不难直接求出两切点坐标。

接下来进行辛普森积分，同样设 \(f(a)\) 表示在该平面直角坐标系上 \(x=a\) 这条直线与阴影部分相交的线段长度，则只需求出其积分值即可。由于该图形在横向和纵向上都是连续的，所以不需要分段求解，也不需要求线段并，直接求与圆和切线相交的长度最大值即可。